
?诗赋清音:烛龙翔夜啸,翼舞星空深。 巍峨山川壮丽志,激荡热血梦侠心。


目录
1. CSAPP与Data Lab简介
1.1 CSAPP
1.2 DataLab
2. DataLab
2.1 实验环境
2.2 实验过程
编辑
2.2.1 bitXor(x,y)
2.2.2 tmin
2.2.3 isTmax
2.2.4 allOddBits
2.2.5 negate
2.2.6 isAsciiDigit
2.2.7 conditional
2.2.8 isLessOrEqual
2.2.9 logicalNeg
2.2.10 howManyBits
2.2.11 floatScale2
2.2.12 floatFloat2Int
2.2.13 floatPower2
2.3 实验结果
2.4 心得体会
1. CSAPP与Data Lab简介
1.1 CSAPP
《CSAPP》是指计算机系统基础课程的经典教材《Computer Systems: A Programmer's Perspective》,由Randal E. Bryant和David R. O'Hallaron编写。该书的主要目标是帮助深入理解计算机系统的工作原理,包括硬件和软件的相互关系,其涵盖了计算机体系结构、汇编语言、操作系统、计算机网络等主题,旨在培养学生系统级编程和分析的能力。
1.2 DataLab
"Data Lab" 实验是指在计算机体系结构和汇编语言等课程中进行的一种实际编程练习。这种实验要求学生编写程序,通常是在汇编语言中,以模拟某种计算机系统或处理器的行为。实现特定指令集的模拟器,或完成一些与底层计算机硬件相关的任务,如内存管理、指令执行等等。这些实验旨在加深对计算机系统的理解,提高编程技能,以及培养解决实际问题的能力。
资源获取:关注公众号【科创视野】回复 csappdatalab
2. DataLab
2.1 实验环境
VMware Workstation虚拟机环境下的Ubuntu 64位。2.2 实验过程
实验准备阶段:首先需要使用ubuntu联网环境跳转到链接下载实验所需的datalab:DateLab源文件
下载datalab压缩包并输入:
tar –xvf datalab-handout.tar
进行解压缩,进入该目录所有文件如下所示:
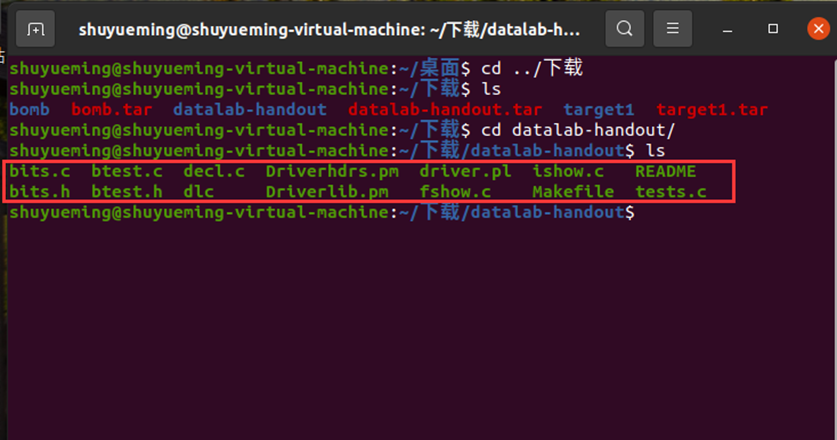
在终端输入下列指令安装make。
sudo apt install gcc-multilib
实验过程阶段:在终端输入vim bits.c进入bits.c文件,其中包含了13个编程谜题中每个谜题的骨架。任务是只使用整数谜题的直线代码(即没有循环或条件)和有限数量的C算术和逻辑运算符来完成每个函数骨架。明确禁止使用任何控制结构,如if,do,while,for,switch等;定义或使用任何宏;在此文件中定义任何其他功能;调用任何功能;使用任何其他操作,例如&&,||, - 或?:使用任何形式的转换使用除int之外的任何数据类型。
具体只能使用以下八个运算符:
! ˜ & ˆ | + << >>
需要解决12个函数,描述如下:
2.2.1 bitXor(x,y)
函数实现的功能等价于
return (x&~y)|(y&~x);
但x||y仅允许使用&和~。
解决思路:
根据德摩根定律将与转化为非和或:
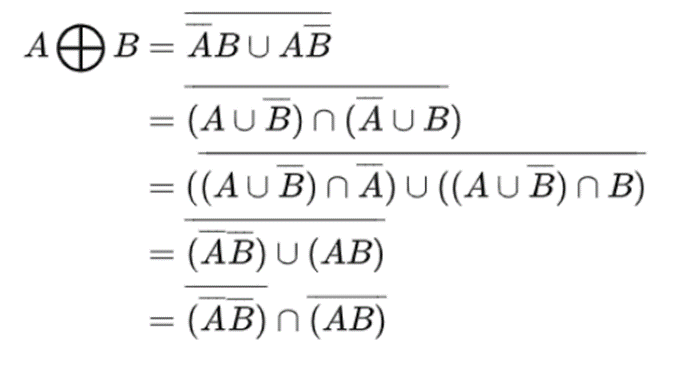
根据德摩根律做数学推导,允许使用的二元运算符只有&,根据x & y的结果有:x & y = 1 (11)x & y = 0(01,10,00),记 ck1= x & y,只要对ck1取反,再排除00就可以了,修改bitXor函数:
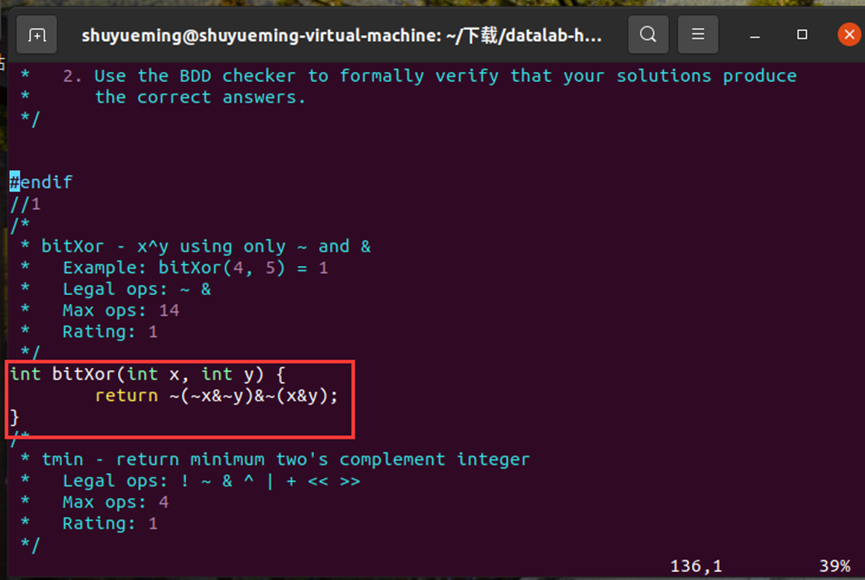
在终端输入下列指令进行验证,结果显示通过。
./btest –f bitXor

在终端输入下列指令进行验证,结果显示通过。
./dlc bits.c
![]()
2.2.2 tmin
tmin函数要求实现返回最小2进制的补码整数。
解决思路:
对于32位机器而言,最小的补码是-1:0xffffffff,整型数最小值为0x80000000。根据题目要求不能直接返回0x80000000。已知8位最小二进制补码为10000000,即1左移7位,所以tmin函数就是符号位为1,其他所有位为0。那么可以使用左移运算符实现,即为0x1<<31。
修改tmin函数如下:
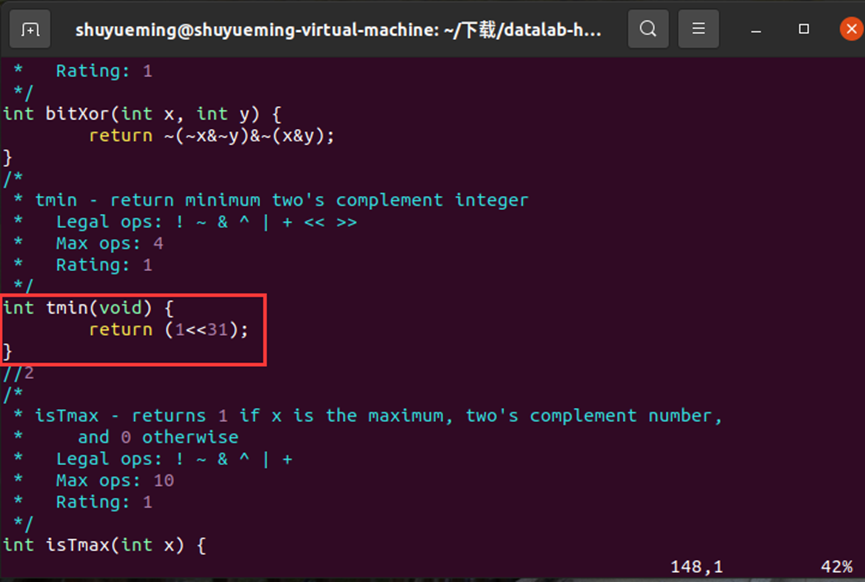
在终端输入下列指令进行验证,结果显示通过。
./btest –f tmin

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.3 isTmax
isTmax函数要求实现如果x是最大值,则返回1,即2的补码。假设x为TMax(01111111,8位),则x+1得到TMin(10000000),再加x,取反再取非,即可返回1,而其余值返回0但因为当x=-1时,最后返回值也为1,所以要排除这种情况。
解决思路:
补码的最大值是0x7FFF FFFF,即二进制中最高位为0,其他位为1。当该值加1时,得到的结果是0x8000 0000,这个值与补码的最大值按位取反相同。因此,可以通过对(x)和(x+1)进行按位异或运算,来判断x是否是补码的最大值。但是需要注意一种特殊情况:当x为0xFFFF FFFF时,x加一后会发生溢出,得到的结果也与其按位取反相同(都为0),因此需要排除此类情况。
修改isTmax函数如下:
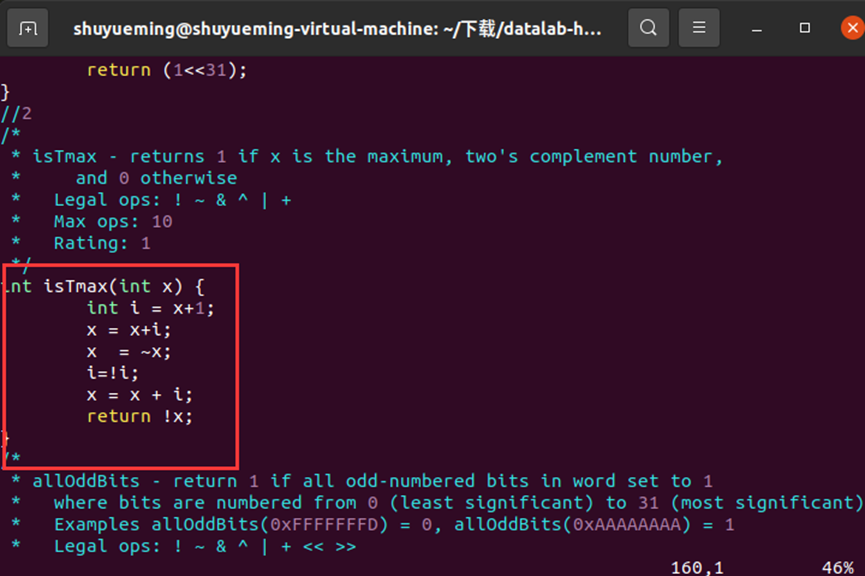
在终端输入下列指令进行验证,结果显示通过。
./btest –f isTmax

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.4 allOddBits
allOddBits要求实现如果字中的所有奇数位都设置为1,则返回1。其中位编号从0(最低有效)到31(最高有效),示例allOddBits(0xFFFFFFFD)=0,allOddBit(0xAAAAAAAA)=1。
解决思路:
当所有奇数位为1,偶数位为0时,得到的值是0xAAAAAAAA。为了判断一个数x是否符合这个规律,可以将x与0xAAAAAAAA进行按位“与运算”,观察结果是否与0xAAAAAAAA相等。如果相等,返回1,否则返回0(可以使用异或运算)。由于本题要求使用的常数不能超过8bit,因此可以使用左移运算来计算0xAAAAAAAA。
修改allOddBits函数如下:
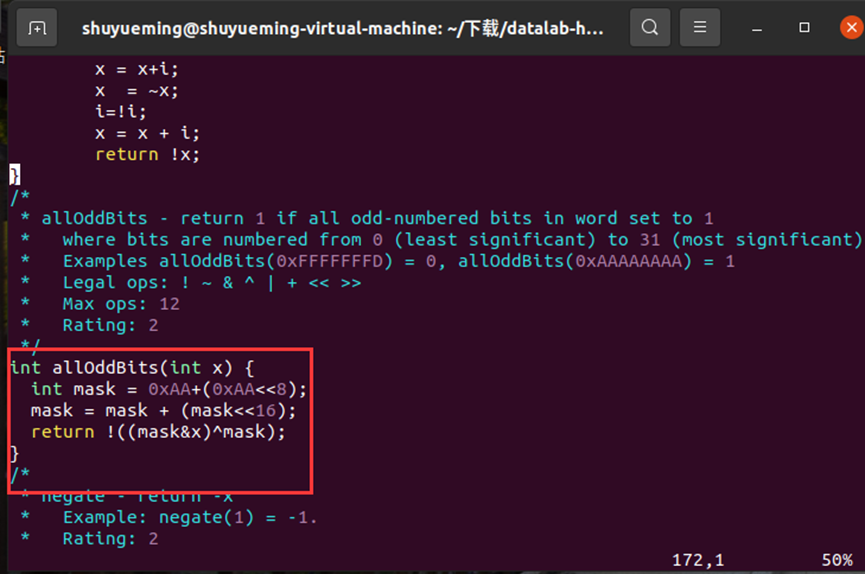
在终端输入下列指令进行验证,结果显示通过。
./btest –f allOddBits

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.5 negate
Negate函数要求实现返回-x,示例:否定(1)=-1。
解决思路:
可以推导出x的负数等于x按位取反加一。可以使用加法逆元进行解释,需要注意的是,在int中并不是每个数都可以通过加负号来求得自己的加法逆元,比如Tmin会发生溢出。但是,对于每个数都可以使用方程x+x”=0来求得一个加法逆元。通过观察可以发现:~x + x = 0xFFFFFFFF,即-1,则有 ~x+x+1 =-1+1 =0,所以x的加法逆元为~x+1。
修改negate函数如下:
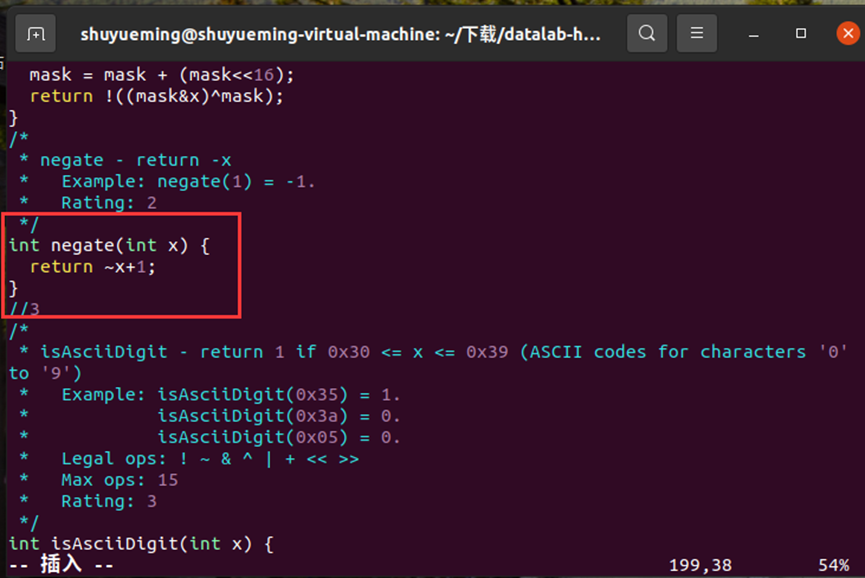
在终端输入下列指令进行验证,结果显示通过。
./btest –f negate

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.6 isAsciiDigit
isAsciiDigit函数要求实现如果x<=y,则返回1,否则返回0。如示例:
isLessOrEqual(4,5)=1
解决思路:
为了实现本题要求,可以将x分别与0x39和0x30进行按位减法运算,然后判断结果的正负关系。但是本题不可以使用“-”符号。受上一道题目的启发,可以使用公式-x=(~x)+1。这样就可以将减法运算转换为加法运算。现在还剩下一个问题,如何判断结果的正负。正数的符号位为0,负数的符号位为1。可以通过左移31位来获取结果的符号位,从而判断结果的正负。
修改isAsciiDigit函数如下:
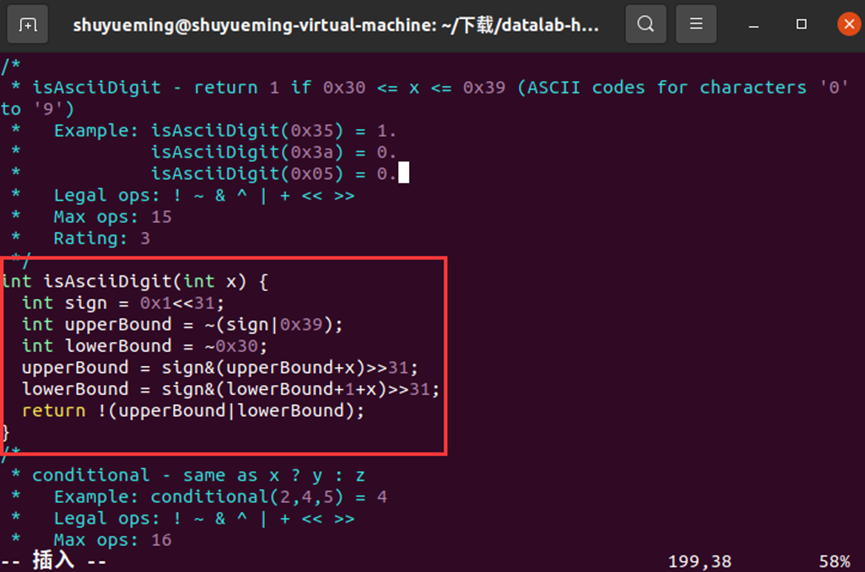
在终端输入下列指令进行验证,结果显示通过。
./btest –f isAsciiDigit

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.7 conditional
Conditional函数要求实现用位级运算表示三目运算符 x?y:z。
解决思路:
可以将返回值分为两种情况,并使用按位或(|)运算将它们连接起来。对于返回y的情况,可以使用补码全1(即-1)与x进行按位与(&)运算,得到一个值为y或0的结果;对于返回z的情况,可以使用0与x进行按位与运算,得到一个值为0或z的结果。
为了将condition与x相关联,可以使用!!x操作将x转换为布尔值,然后使用取相反数的操作(~)得到-1或0的值,将其赋值给condition。最后,将condition与结果进行按位与(&)运算即可得到最终的结果。要使用全1和全0的二进制位与y、z进行位运算。为了区分1和0,并获得全1和全0的二进制表示,可以将得到的值进行取反加一,从而得到condition。这样就可以将1,0变成-1,0。最后,将condition与y按位与,~condition与z按位与,即可得到结果。
修改conditional函数如下:

在终端输入下列指令进行验证,结果显示通过。
./btest –f conditional

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.8 isLessOrEqual
isLessOrEqual函数要求实现如果x<=y,则返回1,否则返回0,例如示例:
isLessOrEqual(4,5)=1
解决思路:
此处可以沿用isAsciiDigit(x)的思路,使用减法和判断符号位的方式来实现。然而需要考虑溢出的情况:
1.y>0且x<0
2.x>0且y<0
其中,当y<0,x>0时,可能出现 y-x>0 负溢出,而当y>0,x<0时,可能出现 y-x<0 正溢出。
因此需要注意处理这两种情况,并根据x,y的符号来判断哪个数更大。如果x,y符号相同,则将标志位设为0(相同),并将其与y-x的符号位为0的结果进行按位与,得到1的结果;如果x,y符号不同,则将标志位设为1(不同),并将其与x的符号位为1的结果进行按位与,得到1的结果。需要注意的是,因为有符号数右移操作为算术右移,所以提取数的符号位要在右移之后进行按位与1的操作,将其格式化,才能得到0或1的结果,可以根据以上计算结果,判断x是否小于等于y。它存在以下几种情况:
1.如果x>y且y-x不为负数,则x>y,返回0;
2.如果x<y,则x<=y,返回1;如果x>y且y-x为负数,则x<y,返回1。
修改isLessOrEqual函数如下:
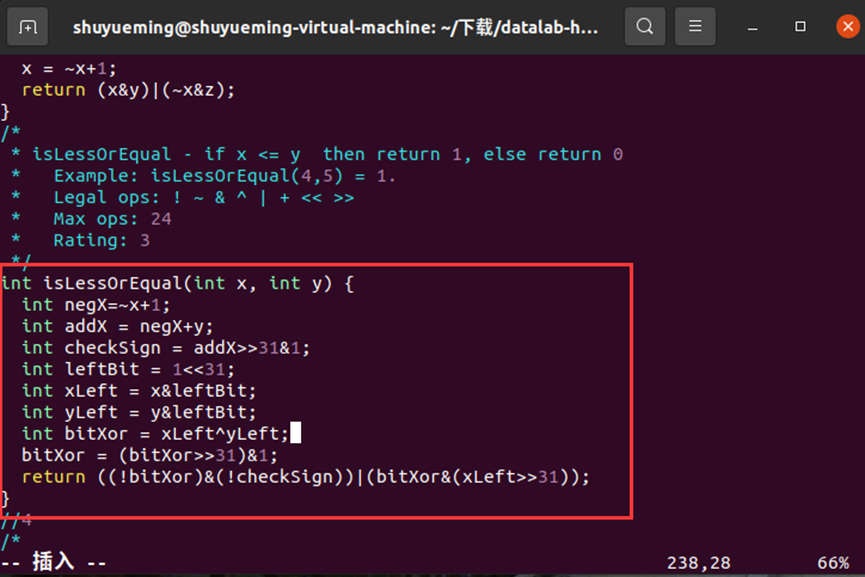
在终端输入下列指令进行验证,结果显示通过。
./btest –f isLessOrEqual

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.9 logicalNeg
logicalNeg函数要求实现实现!运算符,使用所有合法运算(商除外)。例如示例:
logicalNeg(3)=0,logicalNeg(0)=1
解决思路:
根据函数要求我们发现当x为0时,函数返回值为1;当x为其他值时,值与其相反数按位或运算得到的结果的最高位为1,因为值与相反数总有一个是负数。这是因为0的相反数还是0,按位或运算得到的结果还是0,最高位也是0。所以可以先将x与~x+1进行异或操作,然后查看结果的第31位。如果第31位为1,则说明x与~x+1异号,即x和- x的符号不同,否则说明x和- x的符号相同。最后,将结果左移31位,使第31位到达第0位,即可得到0或1的结果,表示两个数的符号是否相同
修改logicalNeg函数如下:
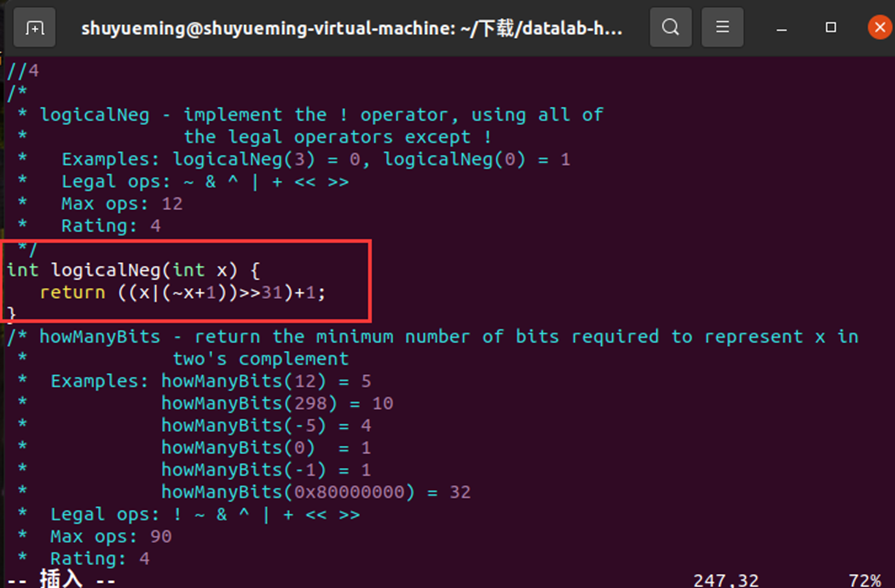
在终端输入下列指令进行验证,结果显示通过。
./btest –f logicalNeg

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.10 howManyBits
howManyBits函数要求实现返回表示x所需的最小位数,例如示例2的补码:
howManyBits(12)=5
howManyBits(298)=10
howManyBits(-5)=4
howManyBits(0)=1
howManyBits(-1)=1
howManyBits(0x80000000)=32
解决思路:
问题的关键是计算这个数第一个“1”出现的位置,为了计算首个“1”出现在第几位,加上符号位后即可得到结果。可以采用二分法的思想,将32位数分为上下两个16位,如果上16位已被使用,则将其左移16位,否则不进行操作。这样问题被缩小了,从求解32位数需要的实际位数,变成了求解16位数需要的实际位数再加上16或是0。以这种方式一次向下查找。需要注意,我们找的位置是最高位的1所在的位置,因此最后的答案应该加上2,但是需要特别处理0和-1的情况。可以将这些特殊情况单独处理,然后依然使用二分法完成计算。
修改howManyBits函数如下:
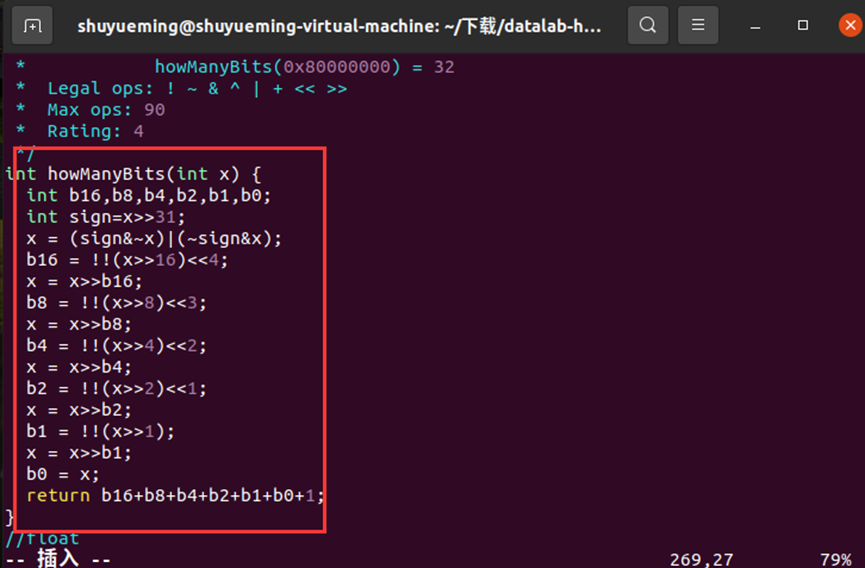
在终端输入下列指令进行验证,结果显示通过。
./btest –f howManyBits

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.11 floatScale2
floatScale2要求实现的内容如下:
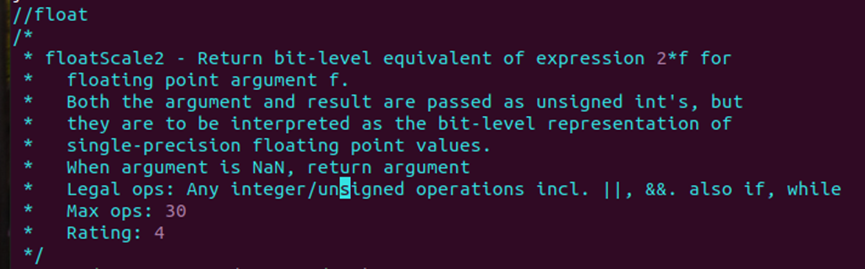
解决思路:
函数的参数和返回值都是无符号整型数。虽然变量uf是一个无符号整型数,但在题目中需要将它的二进制表示解析成一个单精度浮点数。 单精度浮点数的二进制表示如下所示:

根据单精度浮点数的定义,将uf的32个bit位划分为符号位s、阶码字段exp和小数字段frac。提取这三个字段的方法是将uf与0x7F800000按位与运算,再右移23位即可得到阶码字段exp。
从uf中提取符号字段s、阶码字段exp和小数字段frac的方法是将uf与0x7F800000按位与运算,再右移23位即可得到阶码字段exp。经过这步操作已经将无符号整型数解析成单精度浮点数。然后需要根据阶码字段exp的值进行分类讨论。
1.当exp = 0xFF时,表示单精度浮点数为特殊值。特殊值有两种情况:当小数字段frac不等于0时,表示为非数值(NaN);当小数字段frac等于0时,表示为无穷大(正无穷或负无穷)。如果为非数值,则直接返回uf;如果为无穷大,则返回uf,因为对于无穷大乘以2也依然是无穷大。
2.当exp = 0时,表示单精度浮点数为非规格化的数。非规格化的数有两种情况:当小数字段frac等于0时,表示为0,因为0乘以任何数都为0,所以直接返回uf(注意正零和负零的符号位不同,但由于0乘以任何数都为0,故不做讨论,直接返回uf,不能返回0);当小数字段frac不等于0时,表示非常接近于0的数,此时只需将小数字段乘以2即可。
3.当exp不为0且不为0xFF时,表示规格化的数。此时将其乘以2只需要将exp加1即可。
还需要注意一种特殊情况,当阶码字段exp等于254时,虽然是一个规格化的数,但当阶码字段加1后会超出规格化数的表示范围。针对这种情况,我们需要返回无穷大(正无穷或负无穷),根据符号位进行判断即可。
修改floatScale2函数如下:
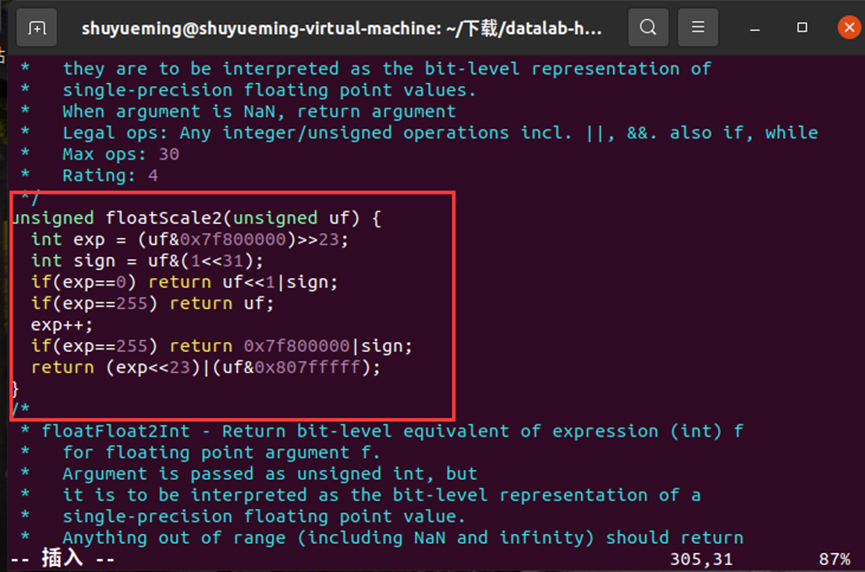
在终端输入下列指令进行验证,结果显示通过。
./btest –f floatScale2

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.12 floatFloat2Int
floatFloat2Int函数要求实现返回表达式(int)f的等效位级别,对于浮点参数f以无符号int形式传递,但它将被解释为单精度浮点值。任何超出范围的东西(包括NaN和无穷大)都应该返回0x80000000单位。
解决思路:
1.当E为0时,表示的数不是整数,因此返回0。
2.当E=31,s=1,V=-2^31或者E=31,s=0,V=2^31时,浮点数所表示的数值超过了整型所能表示的最大值。当E>31时,函数应返回0x80000000u。
3.当E在031之间时,根据exp的值可以判断数据为规格化的数。由于E的取值范围在031之间,而小数字段长度为23位,因此E的范围需分成两种情况进行讨论。
4. 当23 >= E >= 1时,需要对小数字段进行截断处理。如果E = 23,直接返回小数字段;如果E = 22,舍弃小数字段最后一位(右移一位)。
5. 当31 >= E >= 24时,需要对小数字段进行左移处理。如果E = 24,将小数字段左移一位;如果E = 25,将小数字段左移两位。
修改floatFloat2Int函数如下:
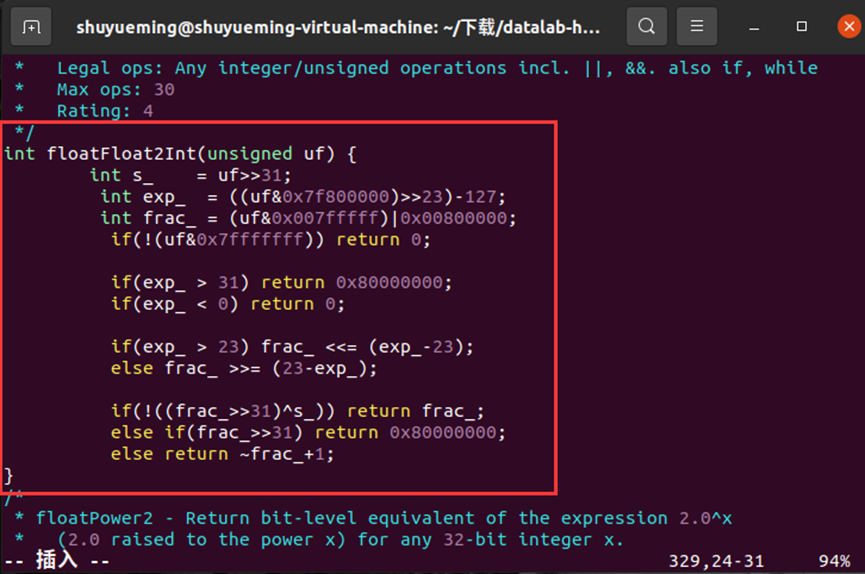
在终端输入下列指令进行验证,结果显示通过。
./btest –f floatFloat2Int

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.2.13 floatPower2
floatPower2函数要求实现表达式2.0^x的原始位级等效项,(2.0的幂x),用于任何32位整数x,返回的无符号值应具有相同的位表示为单精度浮点数2.0^x,如果结果太小,无法用denorm表示,则返回0. 如果太大,返回+INF。
解决思路:
根据函数y = 2^x,为了表示趋近于零的数,我们使用非规格化数,其余使用规格化数。规格化数的最小表示为2的-126次方(E = exp - bias),因此,规格化数与非规格化数的分界线为-127。因此,我们需要根据x的值分类讨论。
1.当exp<=0 时,小于无符号数所能表示的最小值,此时应该返回0;
2.当exp>255 时,超过单精度浮点数所能表示的最大范围,此时应该返回正无穷;
3.其他情况应该右移23位。
修改floatPower2函数如下:
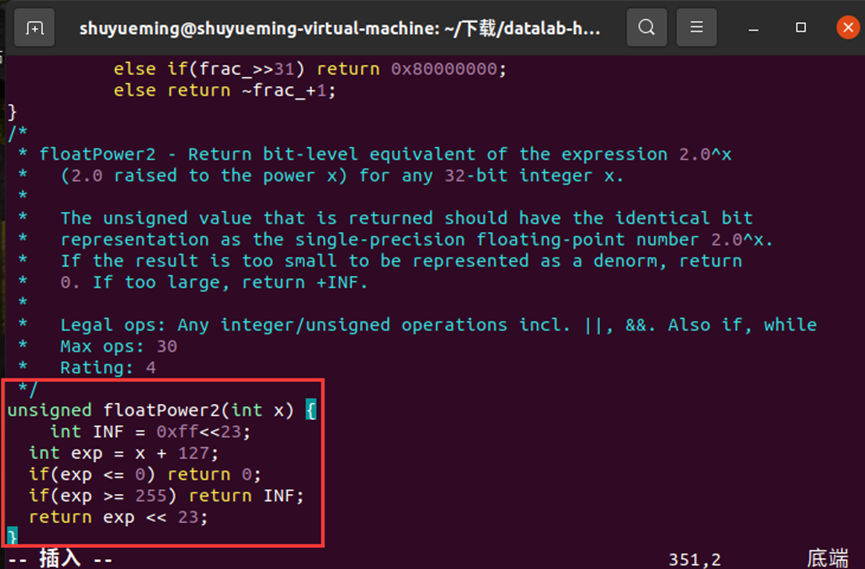
在终端输入下列指令进行验证,结果显示通过。
./btest –f floatPower2

在终端输入下列指令进行验证,结果同样显示通过。
./dlc bits.c
![]()
2.3 实验结果
在终端输入:
./btest
结果显示36/36,说明编写的函数全部通过。
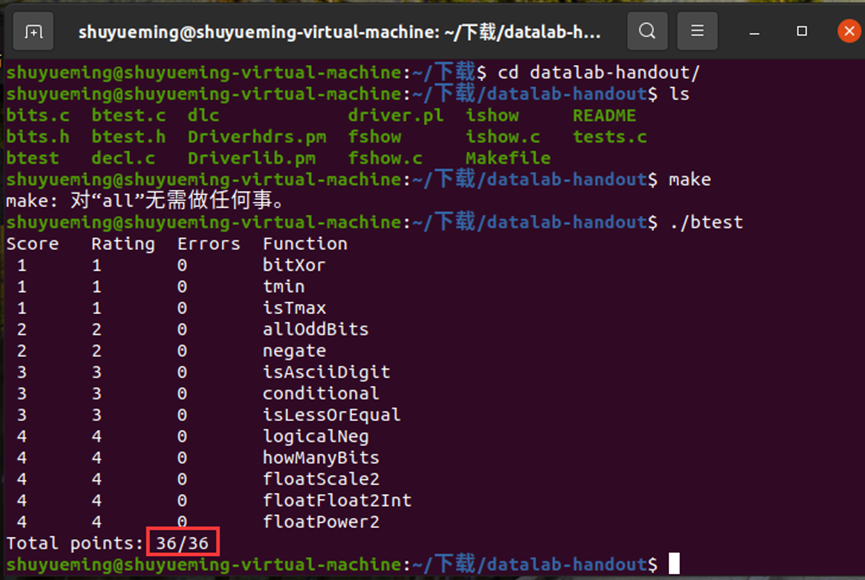
2.4 心得体会
通过本次实验,我深刻体会到了位级运算的重要性,并且对位级运算的理解更加深入。位级运算是一种基础的运算方法,它可以高效地执行各种逻辑运算。在实验中,我学习到了位级运算的基本概念,例如与、或、异或、取反等操作。通过这些操作可以对二进制数进行各种逻辑运算,这对于理解计算机底层原理有很大的帮助。 在实验过程中,我也锻炼了使用位级运算的能力,学会了如何使用位级运算对二进制数进行各种操作。例如使用位掩码来提取二进制数的特定位,使用位移操作来将二进制数向左或向右移动,使用逻辑运算来进行位级运算等。这些操作不仅能够在实验中使用,也可以在编写实际的程序时使用,从而提高程序的效率和性能。 通过datalab实验,我还学习了很多其他的知识。例如IEEE浮点数的存储方式和对浮点数进行位级操作、使用gdb调试程序和makefile进行编译等。


