
?个人主页:努力学编程’
⛅个人推荐:基于java提供的ArrayList实现的扑克牌游戏 |C贪吃蛇详解
⚡学好数据结构,刷题刻不容缓:点击一起刷题
?心灵鸡汤:总有人要赢,为什么不能是我呢

hello,这里提前祝大家五一快乐,每天都能快快乐乐,并且每天都能学到东西。
我们今天继续顺着上次没有说完的排序算法,这里简单复习一下,我们根据每种排序的方式不同,大致上将常见的排序算法分为选择排序,插入排序,交换排序,归并排序。今天就大家学习我们剩下的两个大类,交换排序和归并排序。
?交换排序
⚡冒泡排序
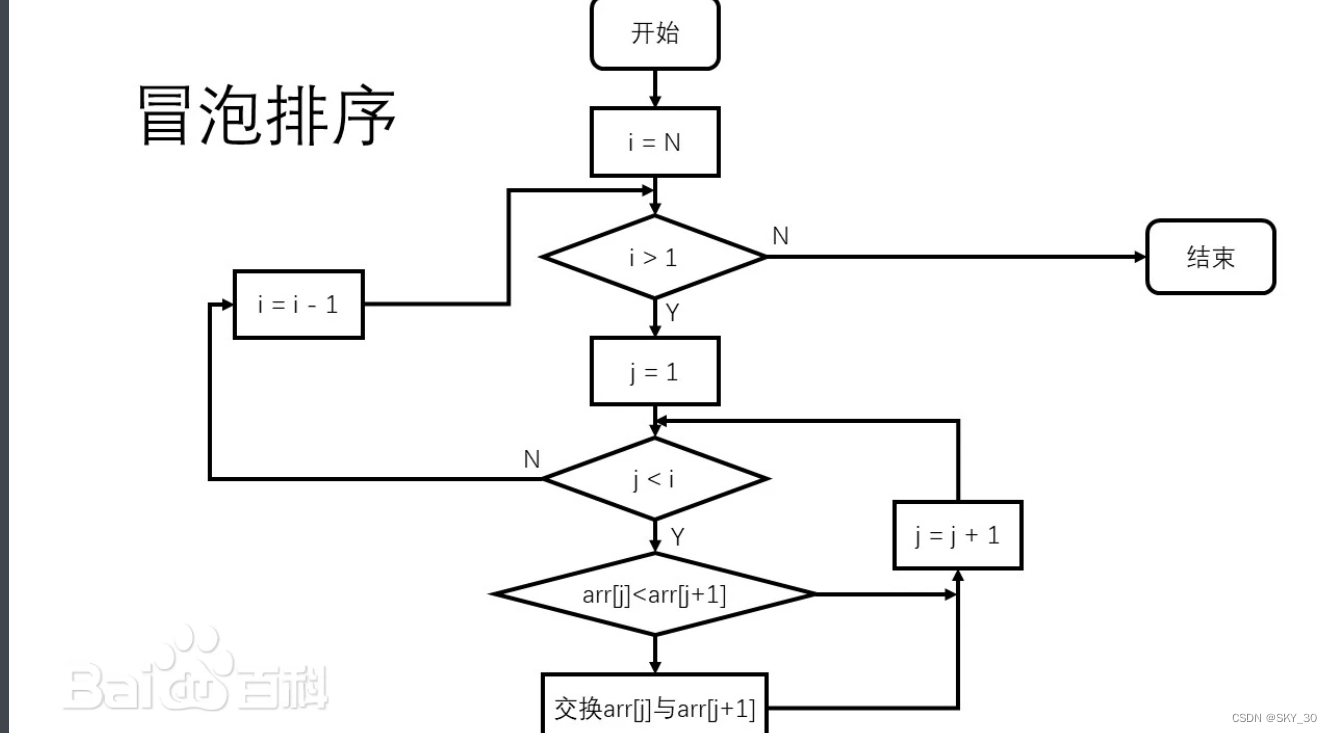
冒泡排序算法的原理如下:
1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2.对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
3.针对所有的元素重复以上的步骤,除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
这里也给大家一个动图,帮助大家理解:
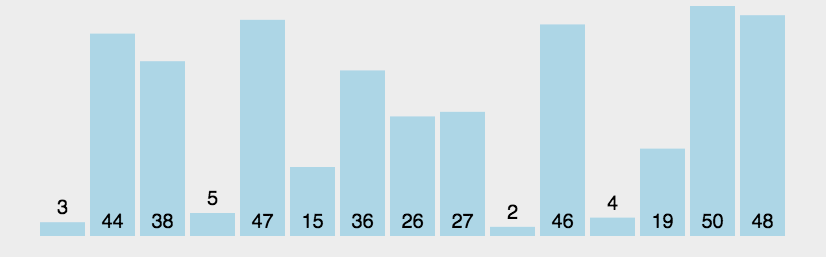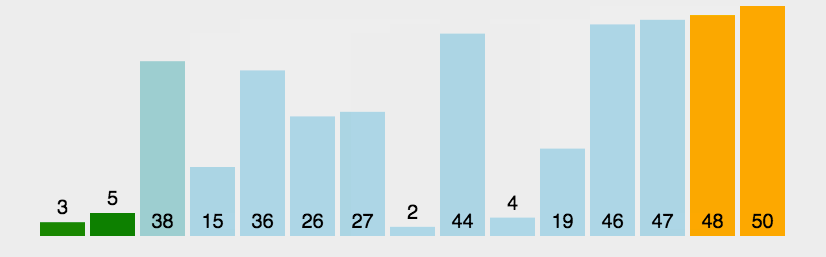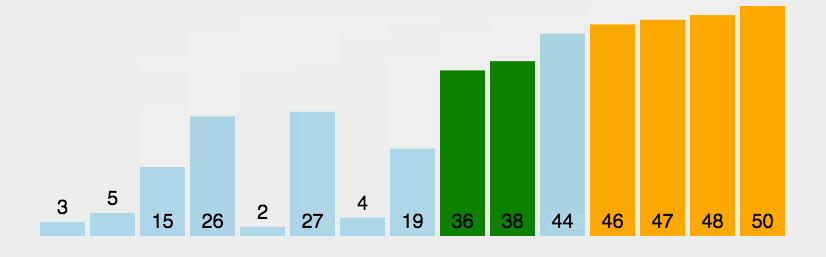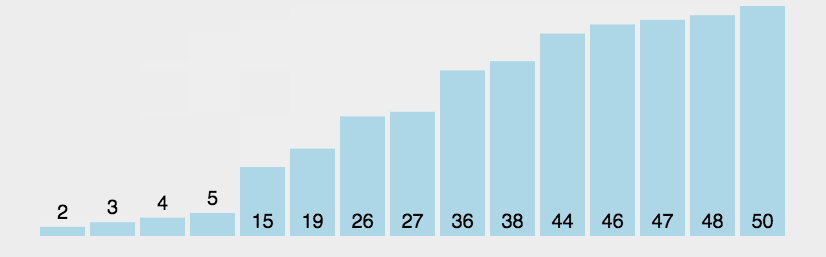
public static void bubbleSort(int[] array) { for (int i = 0; i < array.length-1; i++) { boolean flg = false; for (int j = 0; j < array.length-1-i; j++) { if(array[j] > array[j+1]) { swap(array,j,j+1); flg = true; } } //时间复杂度为:O(N) if(!flg) { break; } } }总体来说呢,冒泡排序是这几种排序中最简单的一种排序,容易理解,代码的逻辑也没有那么复杂,唯一需要提醒大家的,就是两个for循环里面的循环结束条件的判断,这里需要着重强调!!!
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
⚡快速排序
概念:快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
// 假设按照升序对array数组中[left, right)区间中的元素进行排序void QuickSort(int[] array, int left, int right){if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);}这里我们可以根据不的基准值,将快速排序划分为两个版本Hoare版本,和挖坑法。
⛅Hoare法
Hoare法是指在对数组进行排序时,定义两个变量,与一个在单子循环中不变的key值,右值先动找比key小的数字,找到后左值动,找比key大的数字,后进行交换以完成对数组的排序。
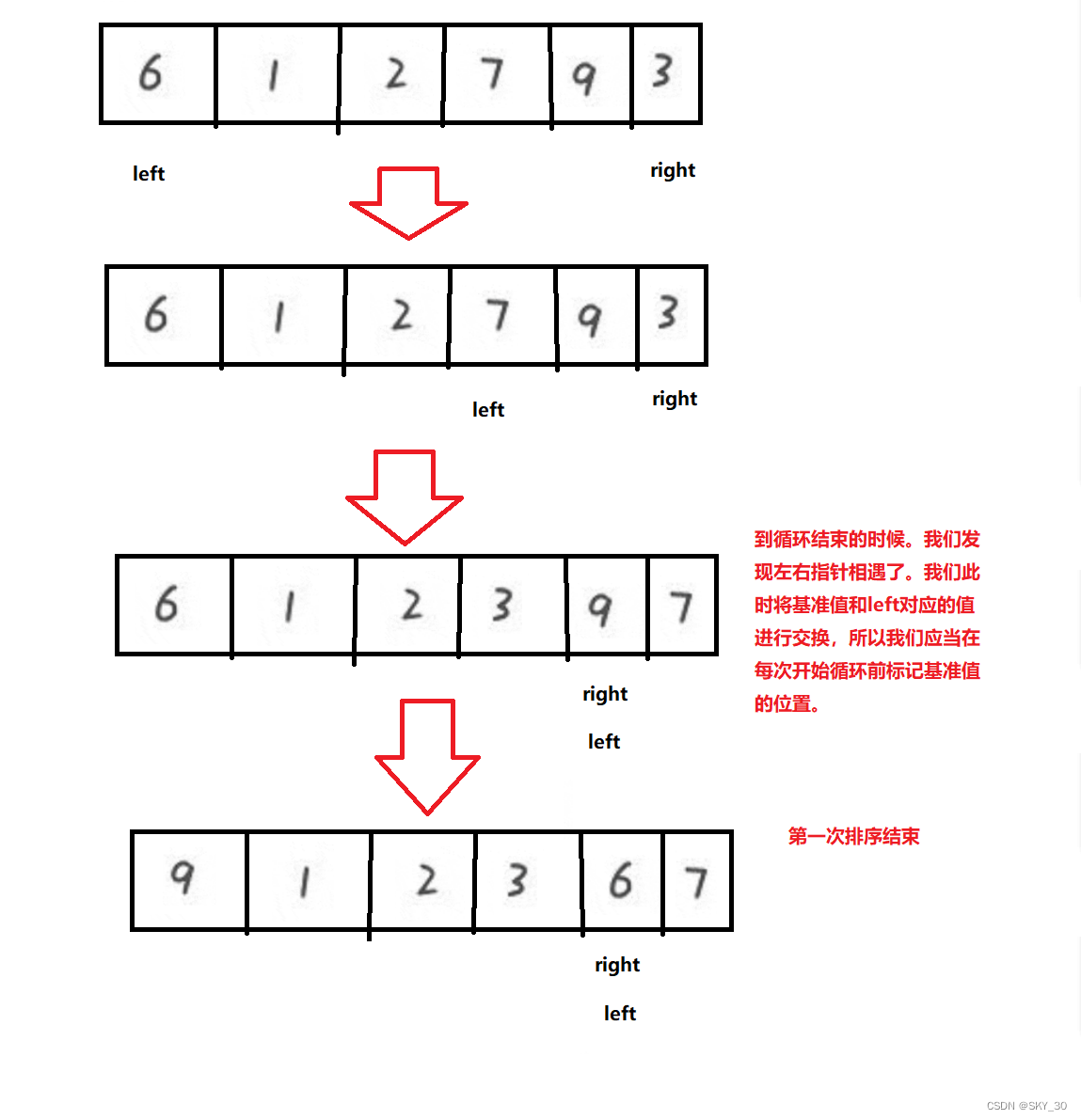
private static int partitionHoare(int[] array,int left,int right) { int i = left; int tmp = array[left]; while (left < right) { //array[right] >= tmp 这里能不能 不取等于号 //不能,自己排序会发现这里取等号排序会混乱 // right--; 为什么先走右边 //先走左边会把数值大的元素换到数组的右边 while (left < right && array[right] >= tmp) { right--; } while (left < right && array[left] <= tmp) { left++; } swap(array,left,right); } //left 和 right 相遇了 swap(array,left,i); return left; }⚡挖坑法
我们上面讲过了Hoare法,其实在一般的快速排序的构成中,我们默认它底层的其实逻辑使用的挖坑法。所以我们这里着重给大家介绍一下挖坑法。
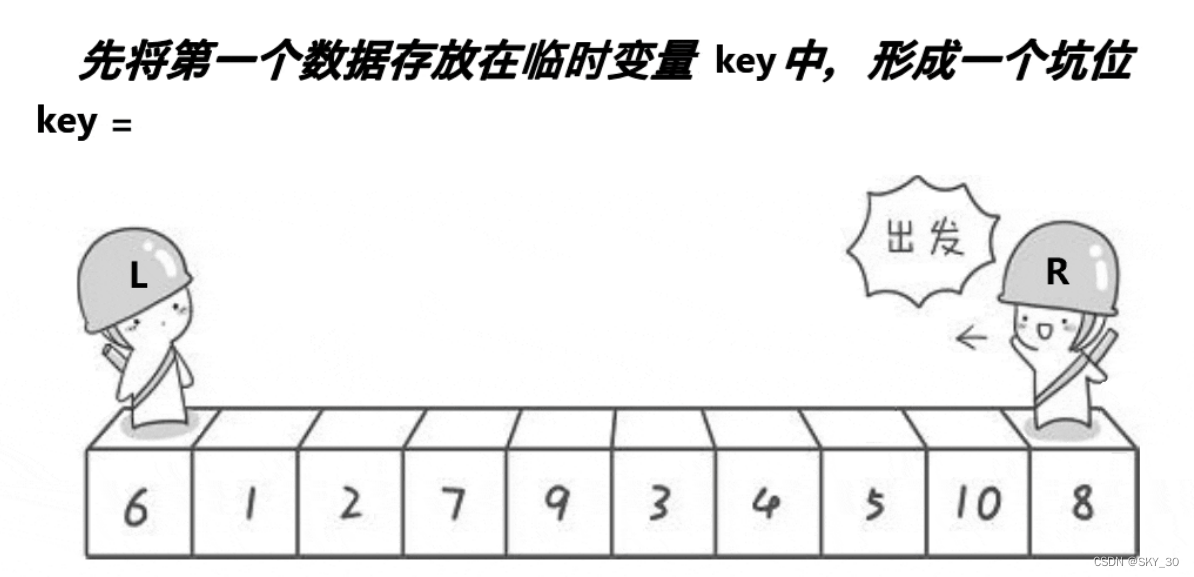
private static int partition(int[] array,int left,int right) { int tmp = array[left]; while (left < right) { while (left < right && array[right] >= tmp) { right--; } array[left] = array[right]; while (left < right && array[left] <= tmp) { left++; } array[right] = array[left]; } array[left] = tmp; return left; }好了,我们这里对实现的挖坑法做一点测试。
⚡归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
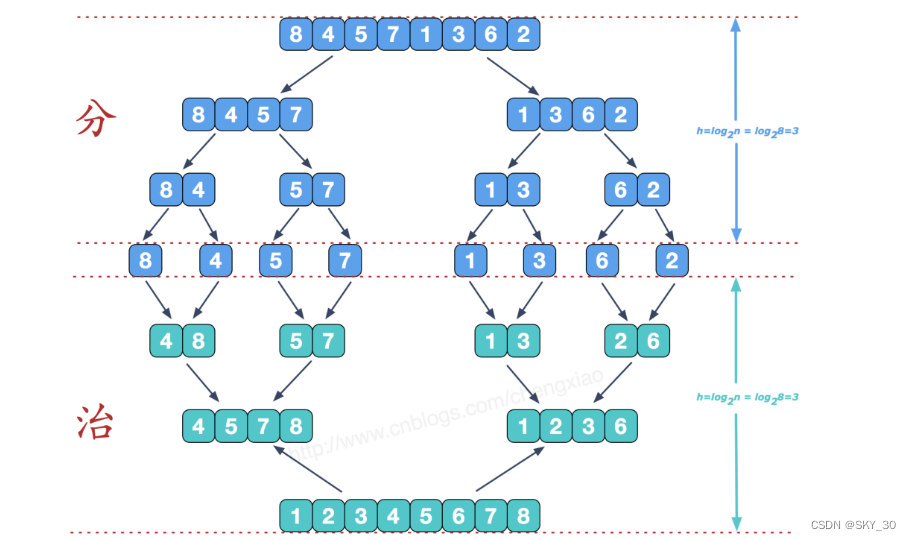
这里我们使用的分而治之的方法,去求解的时候,分相对来说是比较简单的,我们使用递归的方法可以很快的对数组进行分组,然后,我们在合并数组的时候,整个过程邢队来说是比较麻烦的,我们需要先对元素进行排序,然后,申请一块新的数组将已经排好序的元素放到申请的数组当中,然后递归整个过程。
这里也罢代码给大家,仔细看一下注释标注的地方,会有很大收获。
public static void mergeSort(int[] array) { mergeSortFun(array,0,array.length-1); } public static void mergeSortFun(int[] array,int left,int right) { if(left >= right) {// > return; } int mid = (right+left) / 2; mergeSortFun(array,left,mid); mergeSortFun(array,mid+1,right); //合并 merge(array,left,mid,right); } private static void merge(int[] array,int left, int mid,int right) { //这里申请一块新的数组 存放排好序元素 int[] tmp = new int[right-left+1]; int k = 0; int s1 = left; int e1 = mid; int s2 = mid+1; int e2 = right; //定义整个存放元素过程的限制条件 while (s1 <= e1 && s2 <= e2) { if(array[s1] <= array[s2]) { tmp[k++] = array[s1++]; }else { tmp[k++] = array[s2++]; } } //走到这里,可能是左边的数组已经排完了 //我们就把右边所有的元素是直接放到数组当中 //当右边已经拍完之后, //我们需要将左边还剩的元素直接放到数组当中。 while (s1 <= e1) { tmp[k++] = array[s1++]; } while (s2 <= e2) { tmp[k++] = array[s2++]; } //走到这里 相当于tmp数组 当中 所有的元素 都有序了 //接下来把tmp数组的内容 拷贝到array数组当中 for (int i = 0; i < k; i++) { //这里的array()里面的元素索引要加上left,拷贝到原数组 // array[i+left] = tmp[i]; } }归并排序总结
1.归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
?海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
归并排序多用于海量输数据的使用,在整个过程中,我们将海量数据,分成很多一份份的,将每一小份数据单独处理,最后将所有的小数据块进行合并,完成海量数据的处理!!!
?一图带你了解所有排序算法的时间复杂度,和使用场景
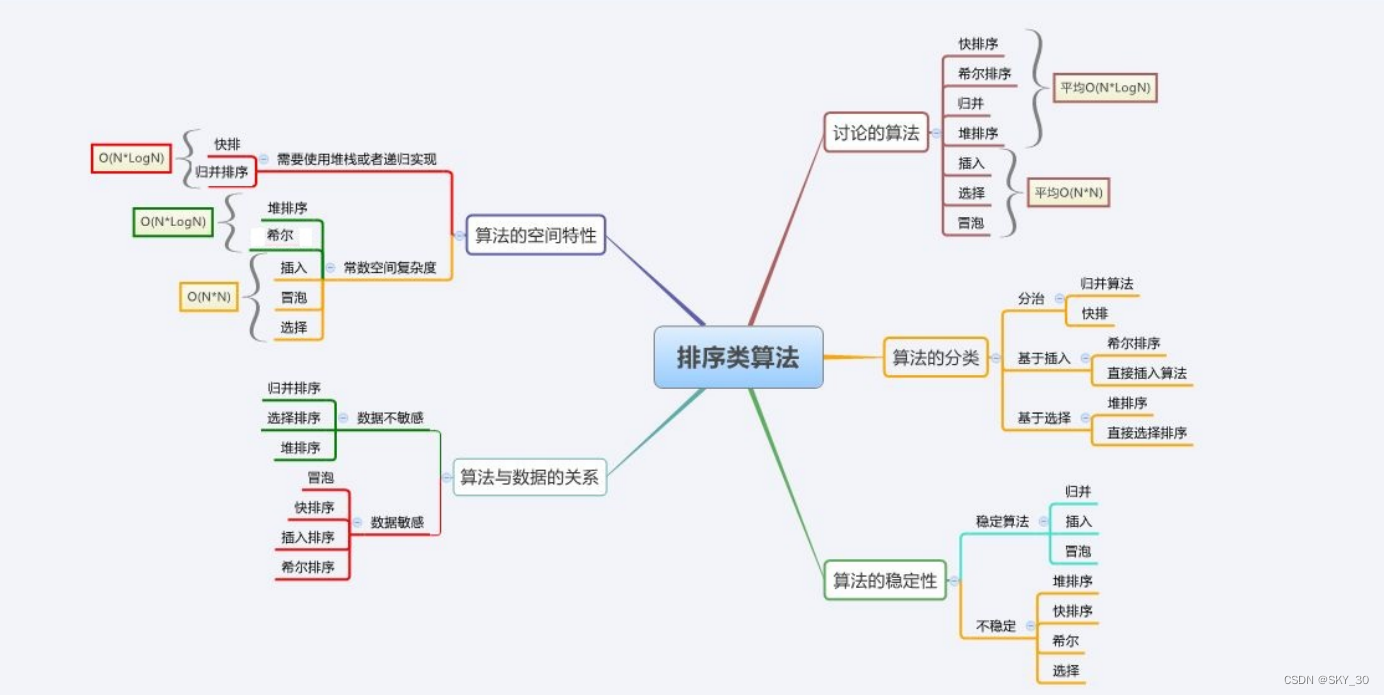
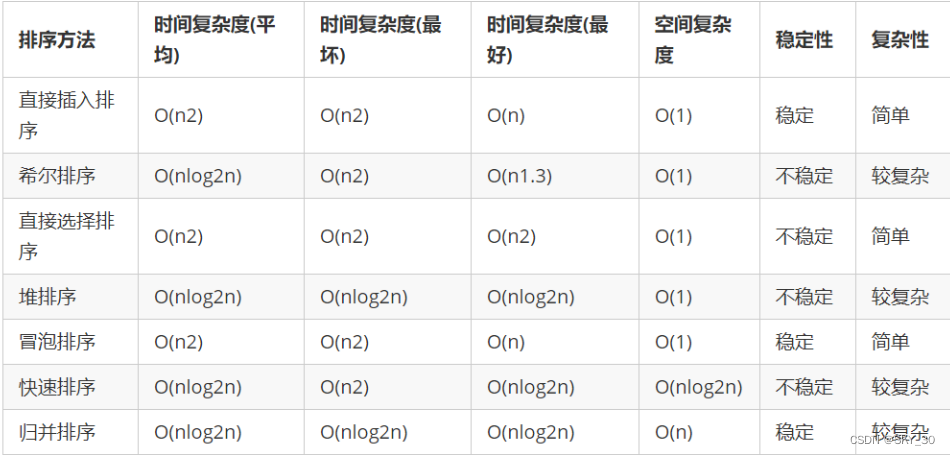
好了,今天就分享到这里,感谢你的阅读!!!