模板引入
一维前缀和
https://www.nowcoder.com/share/jump/9257752291725692504394
解法一:暴力枚举
在每次提供 l 与 r 的时候,都从 l 开始遍历数组,直到遇到 r 停止,这个方法的时间复杂度为 O(N * q)
解法二:前缀和
如果我们事先就知道所有从 0 开始的子数组的前缀和的话,那么要计算 从 l 到 r 之间的字数组的和的时候,我们就可以利用这个已知的前缀和数组进行计算,也就是 ans = dp[r] - dp[l] + nums[l]
时间复杂度为 O(N + q) , 空间复杂度为 O(N)
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); int n = in.nextInt(); int q = in.nextInt(); long[] arr = new long[n]; for(int i = 0; i < n; i++) { arr[i] = in.nextInt(); } //构建前缀和数组 long[] dp = new long[n+1]; for(int i = 1; i <= n; i++) { dp[i] = dp[i-1] + arr[i-1]; } while(q > 0) { int l = in.nextInt(); int r = in.nextInt(); System.out.println(dp[r] - dp[l] + arr[l-1]); q--; } }}二维前缀和
https://www.nowcoder.com/share/jump/9257752291725693083065

解法一:暴力枚举
直接遍历矩阵,时间复杂度为 O(N² * q)
解法二:前缀和
和上面那一道题目一样,我们先预处理一个前缀和数组,只不过这次是一个二维数组,我们需要讨论一下:
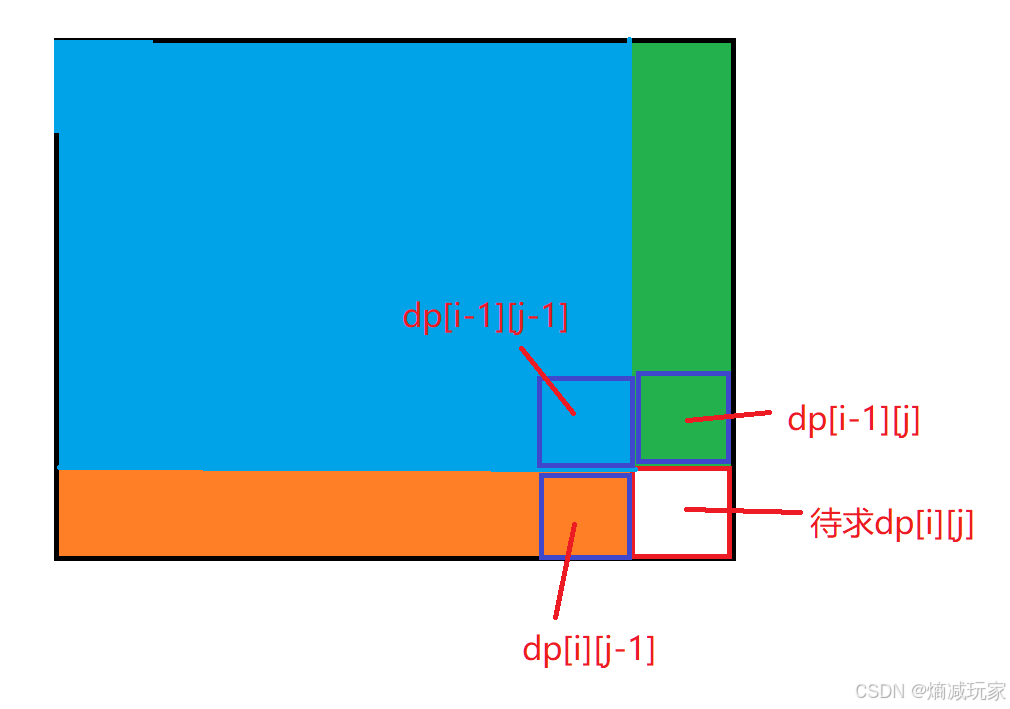
由上图可知,要想求 dp[i][j],我们可以利用上面的关系来推导,也就是 dp[i][j] 等于三块颜色的区域 加上 原矩阵对应的 nums[i][j]
dp[i-1][j] 等于蓝色区域加上绿色区域,dp[i][j-1] 等于蓝色区域加上橙色区域,dp[i-1][j-1] 等于蓝色区域
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + nums[i][j]
但是要注意可能会出现数组越界访问的情况,因为当 i = 0 或者 j = 0 的时候 ,dp[i][j-1] 是会发生越界访问的,所以要避免发生越界访问的话,我们可以加多一个外围区域,就是将 dp 数组 在创建的时候,可以将 dp[][] = new int[n+1][m+1],也就是比原先数组多一行和多一列
这样的话,我们在进行 dp 数组计算的时候,下标就应该从 1 开始,对应的nums 数组的下标则是减一即可。
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + nums[i-1][j-1]
如何获取从 (x1,y1) 到 (x2,y2) 之间的区域的和
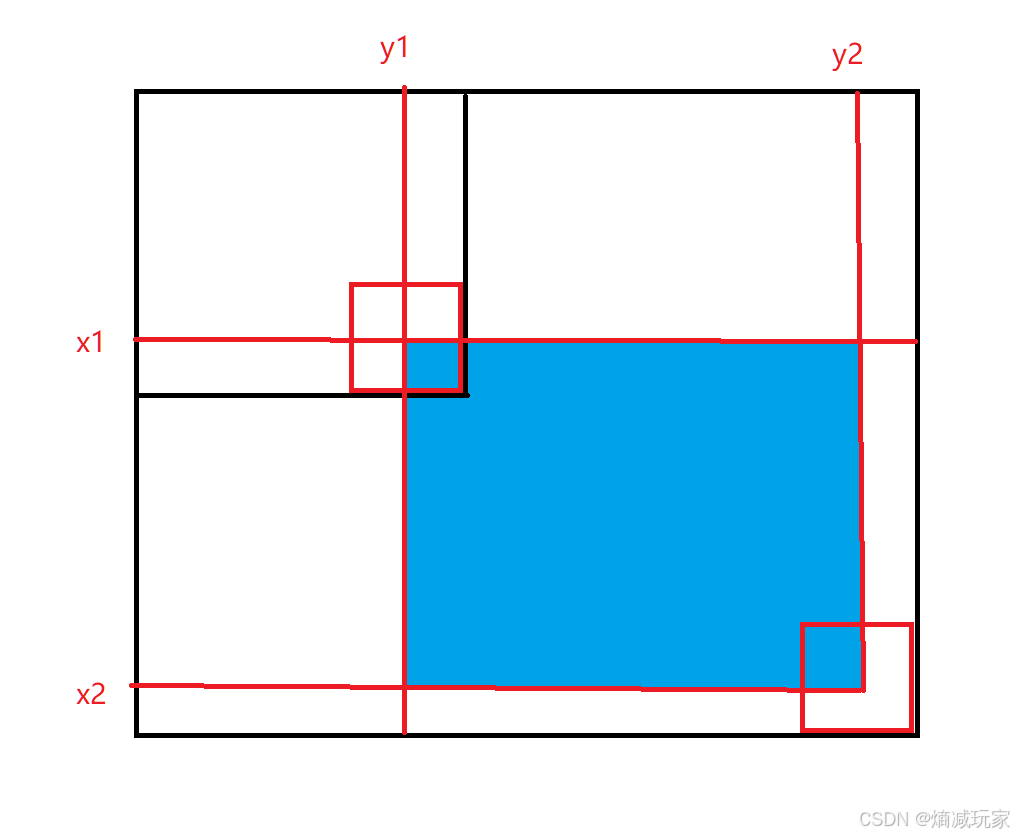
因为正好是x1 ,y1, x2, y2 可以对应我们的 dp 数组,所以直接使用
蓝色区域是我们要求的区域,蓝色区域 等于 = dp[x2][y2] - (dp[x1-1][y2] + dp[x2][y1-1] - dp[x1-1][y1-1]
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); int n = in.nextInt(); int m = in.nextInt(); int q = in.nextInt(); int[][] arr = new int[n][m]; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { arr[i][j] = in.nextInt(); } } //构建前缀和数组 long[][] dp = new long[n+1][m+1]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + arr[i-1][j-1]; } } while(q > 0) { int x1 = in.nextInt(); int y1 = in.nextInt(); int x2 = in.nextInt(); int y2 = in.nextInt(); System.out.println(dp[x2][y2] - (dp[x1-1][y2] + dp[x2][y1-1] - dp[x1-1][y1-1])); q--; } }}小结
前缀和主要用于处理数组区间的和的问题。
前缀和处理二维数组(矩阵)的时候,要注意 dp 数组要扩大。
实战演练
寻找数组的中心下标
https://leetcode.cn/problems/find-pivot-index/description/

解析:
中心下标表示除了这个下标对应的数字之外,其左边区域和等于右边区域和
区域和,我们可以联想到前缀和来解决,由于需要比较左右两边的区域和,我们可以设置前缀和数组与后缀和数组。
注意事项
前缀和应该从 下标 1 开始计算,f[i] = f[i-1] + nums[i-1]
后缀和应该从下标 n - 2 开始计算,g[i] = g[i+1] + nums[i+1]
因为上面两条公式需要利用到之前的前缀和或者后缀和,如果前缀和从0开始计算,则会数组越界访问异常,并且题目告诉我们如果中心下标是最左端,则左侧数组和为 0 ,右侧也一样,所以我们可以直接从 0 或者 n - 2 开始计算。
class Solution { public int pivotIndex(int[] nums) { int n = nums.length; int[] f = new int[n]; int[] g = new int[n]; //构建前缀和数组 for(int i = 1; i < n; i++) { f[i] = f[i-1] + nums[i-1]; } //构建后缀和数组 for(int i = n - 2; i >= 0; i--) { g[i] = g[i+1] + nums[i+1]; } //查找 for(int i = 0; i < n; i++) { if(f[i] == g[i]) return i; } return -1; }}除自身以外数组的乘积
https://leetcode.cn/problems/product-of-array-except-self/description/

解析:
和上面的题目类似,这次是乘法,我们可以使用前缀积和后缀积来解答
这里要注意 f[0] 和 g[n-1] 要先预设置为 0,避免后续计算的时候得到的全是 0
class Solution { public int[] productExceptSelf(int[] nums) { int n = nums.length; int[] f = new int[n]; int[] g = new int[n]; f[0] = 1; g[n-1] = 1; //构建前缀积数组 for(int i = 1; i < n; i++) { f[i] = f[i-1] * nums[i-1]; } //构建后缀积数组 for(int i = n - 2; i >= 0; i--) { g[i] = g[i+1] * nums[i+1]; } int[] ans = new int[n]; for(int i = 0; i < n; i++) { ans[i] = f[i] * g[i]; } return ans; }}和为 K 的子数组
https://leetcode.cn/problems/subarray-sum-equals-k/description/

注意这里不能使用滑动窗口来解决!!!
滑动窗口有一个特点就是右指针不能进行回退,所以当你要使用滑动窗口来解决子数组的时候,要保证一个前提:数组具有单调性。
而这道题目由于数组可能会出现负数,也就是说明数组是不具有单调性的,举个例子:
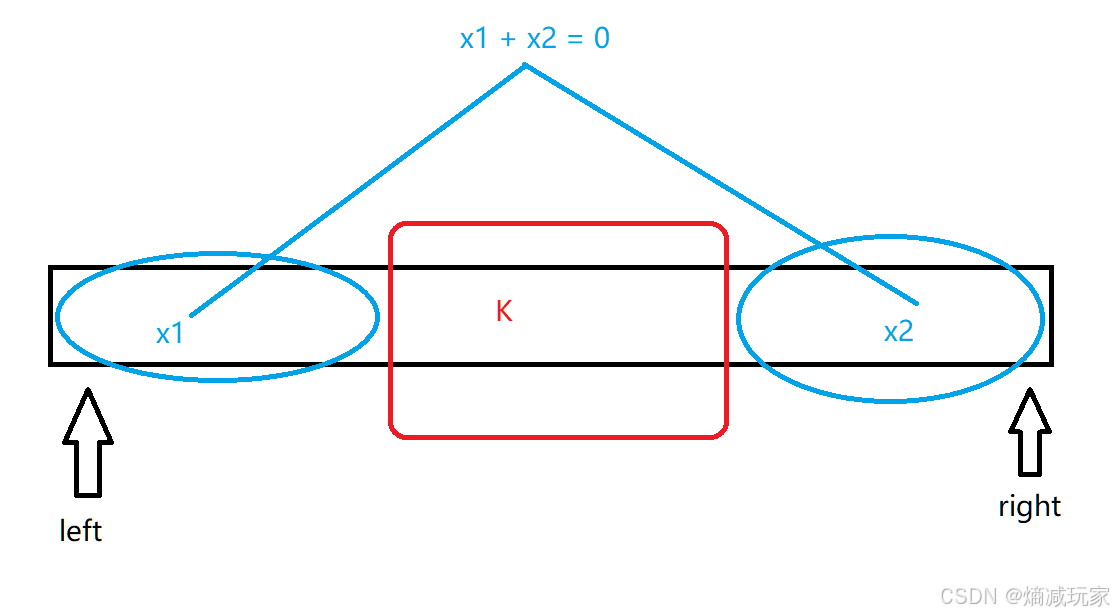
两块蓝色区域相加正好等于零,而中间红色区域等于K 的时候,你使用滑动窗口,由于右指针不能回退,导致遗漏掉中间红色数组的情况,所以,我们不能使用滑动窗口。
解法一:暴力枚举
通过两层 循环,获取所有的子数组,时间复杂度为 O(N²)
解法二:前缀和加哈希表
计算 [0, i] 区间的前缀和 sum[i]
我们把要求的 K 子数组定义为以 i 结尾的子数组
如果存在 K 的子数组的话:
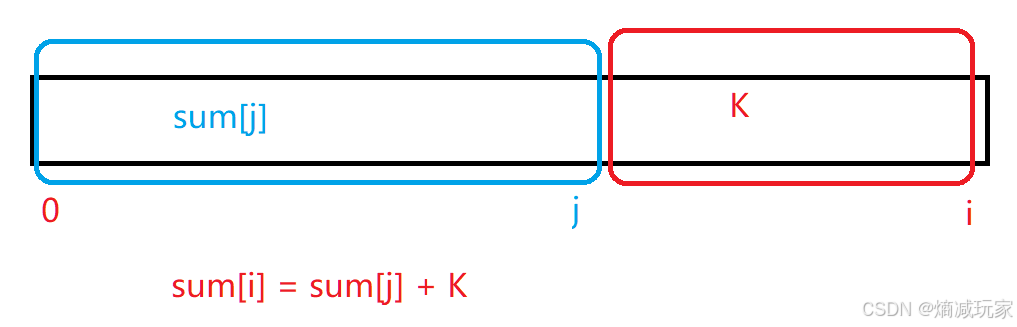
那么如果 i 数组前面出现过 子数组和为 sum[j] 的话,就说明存在 K 数组,sum[j] = sum[i] - K
我们在计算 前缀和 sum[i] 的时候,其实也就已经得知 i 数组前面所有的下标的前缀和,那么我们可以利用哈希表来保存这些数据,哈希表存储的应该是 <sum[i], 出现的次数>
我们其实不需要创建前缀和数组
因为我们只是要利用前一个前缀和结果来推导现在这一个前缀和,对于前几次的前缀和结果我们其实用不到,所以我们可以使用一个变量 sum,一直滚动累加下去即可。
要事先将 <0,1> 存进哈希表中
因为可能会出现一开始就得到 和为 K 的数组,此时 sum - k = 0,但是 count 却没有自增,所以我们事先设定存在一个前缀和 为 0 的子数组,并且出现次数为 1
class Solution { public int subarraySum(int[] nums, int k) { Map<Integer,Integer> map = new HashMap<>(); map.put(0,1); int sum = 0; int count = 0; for(int x : nums) { sum += x; if(map.containsKey(sum - k)) { count += map.get(sum-k); } map.put(sum,map.getOrDefault(sum,0) + 1); } return count; }}和可被 K 整除的子数组
https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/

解析:
这里依旧不能使用滑动窗口来做
因为存在负数,不具有单调性。
补充知识:同余定理,当 (a - b) % p = 0 可以推导出 a % p = b % p,有了这个公式,我们就可以得出当存在另外几个 b 满足 a % p = b % p 的时候,则说明存在 和可被 K 整除的子数组,在判断的时候,我们用到的是余数,所以在哈希表中,我们保存的应该为 <余数,余数出现的次数>,后面就是基本的前缀和操作了,和上面那一道题目类似。
Java 当中,负数 % 正数 的结果为 负数,我们需要将结果纠正为正数,公式为 ret = (sum % k + k) % k
解释一下,sum % k 可以得到余数,但是可能为负数,所以再加 一个 k,保证这是一个正数,但是可能会破坏余数这个特性,所以还要再次 模 k,最后的 模k 是不会影响的。
由于可能会出现一开始前缀和 正好为 K ,取模结果为0,此时应该预先将 <0,1> 存储进哈希表里。
class Solution { public int subarraysDivByK(int[] nums, int k) { Map<Integer,Integer> map = new HashMap<>(); map.put(0,1); int sum = 0; int count = 0; for(int x : nums) { sum += x; int ret = (sum % k + k) % k; count += map.getOrDefault(ret, 0); map.put(ret,map.getOrDefault(ret,0) + 1); } return count; }}连续数组
https://leetcode.cn/problems/contiguous-array/description/

解析:
由于数组只会出现 0 或者 1,我们要寻找最大长度的数组(满足 0 的数量等于 1 的数量),如果要使用前缀和,我们可以将 0 设置为 -1,这样,我们要寻找的子数组(记为 K)的和就是为 0
前缀和数组sum[i] :
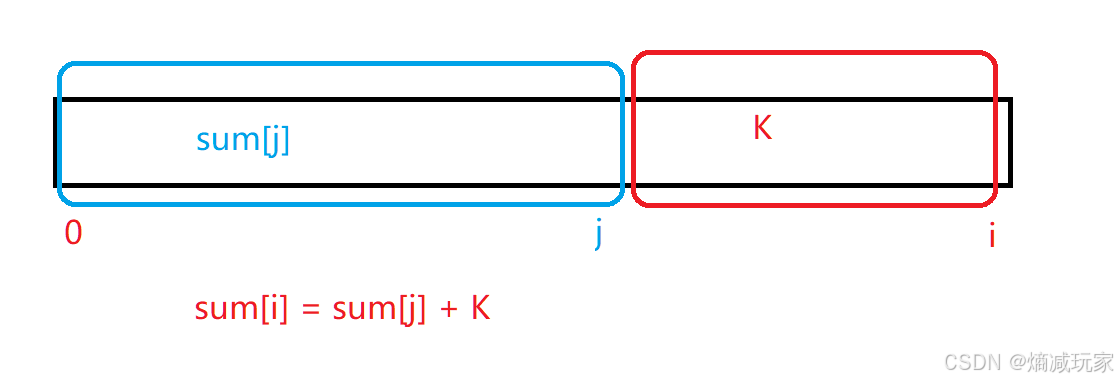
此时 K = 0,那么 就是要得到目前是否存在 sum[j] 数组是等于 sun[i],如果存在,则需要计算这个 K 数组的区间长度 = i - j
于是我们可以将前缀和 与 对应的下标索引 存到哈希表里,<sum,下标>
我们不用真的创建一个前缀和数组,因为我们用不到,我们可以使用一个变量 sum 来保存当前的前缀和结果
如果当整个数组的和为 K 的时候,那么最大的长度应该为 整个数组的长度,此时 i 最大到达 nums.length - 1 ,要想获得 数组长度,我们应该预先将 <0, -1> 存储进哈希表中
哈希表的 put :
我们保存数据的时候,要保存的是 sum 对应的最小的索引,因为我们要求的是最大的数组长度,所以当哈希表存在 sum[i] 的时候,我们应该更新最新长度,这个时候,就不用保存进哈希表里了,因为我们不需要跟新下标索引值,如果没有出现的话,那么此时 sum[i] 所对应的下标要一起保存进哈希表中。
class Solution { public int findMaxLength(int[] nums) { Map<Integer,Integer> map = new HashMap<>(); map.put(0,-1); int n = nums.length; int sum = 0; int maxLength = 0; for(int i = 0; i < n; i++) { sum += (nums[i] == 0 ? -1 : 1); if(map.containsKey(sum)) { int j = map.get(sum); maxLength = Math.max(maxLength,i - j); } else { map.put(sum,i); } } return maxLength; }}矩阵区域和
https://leetcode.cn/problems/matrix-block-sum/description/

解析:
这道题目就是二维数组前缀和的使用
我们先创建好前缀和数组,然后锁定求解的区域,最后计算即可
这里要注意的是前缀和数组要和我们的最终数组要一一对应
class Solution { public int[][] matrixBlockSum(int[][] mat, int k) { int n = mat.length; int m = mat[0].length; int[][] dp = new int[n+1][m+1]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1]; } } int[][] ans = new int[n][m]; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { int r1 = (i - k <= 0 ? 1 : i - k + 1); int c1 = (j - k <= 0 ? 1 : j - k + 1); int r2 = (i + k >= n ? n : i + k + 1); int c2 = (j + k >= m ? m : j + k + 1); ans[i][j] = dp[r2][c2] - (dp[r1-1][c2] + dp[r2][c1-1] - dp[r1-1][c1-1]); } } return ans; }}