哈希表的概念
哈希表(Hash Table)是一种高效的数据结构,用于实现快速的数据存储和检索。它通过将数据映射到一个数组的索引位置,从而能够在平均情况下实现O(1)的时间复杂度进行查找、插入和删除操作。
哈希表的基本概念包括以下几个部分:
哈希函数:哈希表使用哈希函数将输入的数据(通常是键)转换为固定大小的数组索引。一个好的哈希函数能够有效地将不同的数据映射到不同的索引,减少冲突的概率。
冲突处理:由于不同的键可能会通过哈希函数映射到相同的索引,这种情况被称为冲突。常见的冲突处理方法有链地址法(在同一个索引处使用链表存储所有冲突的元素)和开放地址法(通过探测寻找下一个可用的索引)。
负载因子:负载因子是哈希表中存储的元素数量与哈希表大小的比率。负载因子过高会导致冲突增加,影响性能,因此通常在达到一定的负载因子后会对哈希表进行扩展和重新哈希。
哈希表在实际应用中广泛用于快速查找和存储数据,例如数据库索引、缓存系统等,是一种非常实用的数据结构。
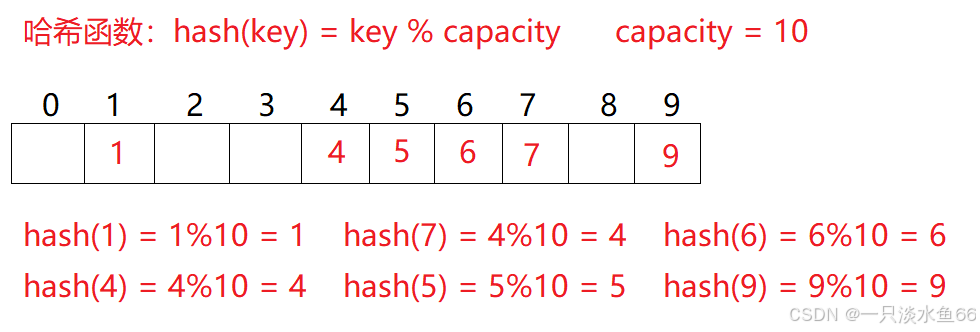
例如:数据集合{1,7,6,4,5,9}。
哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小。
哈希冲突的概念
哈希冲突(Hash Collision)是指在哈希表中,不同的输入数据(通常是键)经过哈希函数处理后,得到了相同的哈希值,进而映射到了哈希表的同一个索引位置。这种现象不可避免,因为哈希函数将任意大小的数据映射到固定大小的数组索引,而输入数据的范围通常大于输出哈希值的范围,从而导致不同的数据可能会对应相同的哈希值。
哈希冲突的处理方法:
为了有效地处理哈希冲突,主要有以下几种常见的方法:
链地址法(Separate Chaining):
在哈希表的每个索引位置,使用一个链表或其他数据结构来存储所有哈希值相同的元素。这样,当发生冲突时,新元素可以直接添加到链表中。优点:实现简单,容易扩展,链表的长度通常是较短的,性能受到较少影响。缺点:当冲突严重时,链表长度增加,会影响查找性能。开放地址法(Open Addressing):
当发生哈希冲突时,哈希表会寻找下一个空闲的位置,将新元素放入该位置,而不是在同一索引位置存储。包括线性探测、二次探测和双重哈希等具体策略来寻找空位。优点:内存占用较低,数据存储在连续的数组中,缓存友好。缺点:可能导致“聚集”现象,即连续的多个元素都占据相邻的索引,影响性能。哈希冲突的影响:
哈希冲突的存在会对哈希表的性能产生影响,特别是在查找、插入和删除元素时。冲突越多,导致的查找时间可能从O(1)增长到O(n)(在最坏的情况下)。因此,选择合适的哈希函数以减少冲突的发生,以及选择有效的冲突处理策略,是设计高效哈希表的关键。
避免哈希冲突的方法
哈希函数设计
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。 哈希函数设计原则:
哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间。哈希函数计算出来的地址能均匀分布在整个空间中。哈希函数应该比较简单。常见哈希函数
直接定制法
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B 优点:简单、均匀 缺点:需要事先知道关键字的分布情况 使用场景:适合查找比较小且连续的情况。
除留余数法
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址。
平方取中法
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址; 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况。
折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。
负载因子调节
负载因子(Load Factor)是哈希表中一个重要的度量,用于评估哈希表的使用效率和性能。负载因子定义为哈希表中存储的元素数量与哈希表的总容量(即数组大小)之间的比率,通常用公式表示为:
负载因子 = 当前元素数量 / 哈希表的容量
负载因子的意义:
性能指标:负载因子能够反映哈希表的性能。当负载因子较低时,哈希表中的元素分布较为稀疏,冲突较少,查找、插入和删除操作的效率较高。而当负载因子较高时,冲突可能增多,导致这些操作的性能下降。
自适应调整:为了保持哈希表的高效性能,通常在负载因子达到一定阈值时(例如0.7或0.75),会进行负载因子的调节。调节方法通常包括扩展哈希表的容量,并重新计算所有元素的哈希值以保证它们被均匀分布。
负载因子的调节过程:
扩展哈希表:当负载因子超过预设阈值时,哈希表需要扩展容量,通常会将哈希表的容量增加为原来的两倍,或者其他合适的数值。
重新哈希:扩展容量后,所有现有元素必须经过哈希函数重新计算哈希值,并根据新容量重新分配到新的索引位置。这一过程被称为重新哈希(Rehashing)。
减少容量:在某些情况下,如果哈希表中的元素数量显著减少,负载因子低于某一阈值,可能会考虑缩减哈希表的容量,以减少空间浪费。
总结:
通过合理地调节负载因子,可以保持哈希表高效的性能,降低冲突率,并确保在各种操作下的时间复杂度保持尽可能接近O(1)。在设计哈希表时,选择合适的负载因子阈值和扩展策略是至关重要的。
解决哈希冲突的方法
开放地址法(闭散列)
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。
线性探测
线性探测(Linear Probing)是一种开放地址法的冲突解决策略,主要用于处理哈希表中的哈希冲突。当多个元素通过哈希函数映射到相同的索引位置时,线性探测使用线性搜索的方法寻找下一个可用的位置来存放新元素。
线性探测的工作原理:
哈希插入:
当需要插入一个元素到哈希表时,首先计算该元素的哈希值,找到其对应的数组索引。如果该索引位置已经被占用(发生冲突),则按顺序检查后续的索引(即当前索引 + 1,当前索引 + 2,依此类推)。继续检查直到找到一个空闲的索引位置,将新元素插入。哈希查找:
查找一个元素时,同样计算出其哈希值并找到对应的索引。如果该位置的元素与查找的元素不匹配,就沿着线性探测的方式依次检查下一个索引。如果遇到空位,说明该元素不在表中;如果找到匹配的元素,则返回该元素。哈希删除:
删除元素时,可以简单地将对应的索引位置设置为“删除”状态(或特殊标记),但仍需注意后续查找时的线性探测,以防止链式冲突查找的失败。线性探测的优缺点:
优点:
实现简单,逻辑清晰。在有序的序列中存储元素时,能够保持元素的连贯性,提高缓存命中率。缺点:
聚集现象(Clustering):线性探测容易导致“聚集”现象,即相邻的元素趋向于占用相邻的索引,这会影响后续插入和查找的效率。在负载因子较高时,性能会显著下降,查找时间可能接近O(n)。总结:
线性探测是一种简洁而有效的冲突解决策略,适用于负载因子较低的哈希表。在负载因子过高时,考虑其他冲突解决方法(如链地址法或二次探测)可能会得到更好的性能表现。
二次探测
二次探测(Quadratic Probing)是一种开放地址法的冲突解决策略,用于哈希表中处理哈希冲突。与线性探测不同,二次探测通过使用平方函数生成一个探测序列,以寻找下一个可用的位置。
二次探测的工作原理:

哈希查找:
查找一个元素时,同样计算出其哈希值并找到对应的索引。如果该位置的元素不匹配所查找的元素,则按二次探测的方式依次检查后续索引(即使用平方探测公式)。如果遇到空位,说明该元素不在表中;如果找到匹配的元素,则返回该元素。哈希删除:
删除元素时,可以将对应的索引位置设置为“删除”状态(或特殊标记),这需要特别注意,因为后续查找仍会使用该位置进行探测。二次探测的优缺点:
优点:
相比线性探测,二次探测能减少聚集现象(Clustering)。由于索引在探测中不再是线性分布,避免了多个元素趋向于占用相邻空间的问题。在一定程度上,能够提高查找和插入操作的效率,特别是当负载因子较高时。缺点:
由于使用平方函数,可能形成某些未探测到的索引,从而造成一些空间浪费。实现相对较复杂,特别是在处理数组大小不是2的幂时,可能需要额外的处理逻辑以确保探测的覆盖性。总结:
二次探测是一种有效的冲突解决策略,适用于哈希表需要保持较低负载因子且冲突较多的情况。通过减少聚集现象,二次探测可以在一定程度上提高哈希表的效率,但在实现上需要关注数组大小和探测方式的合理性。
链地址法(开散列)
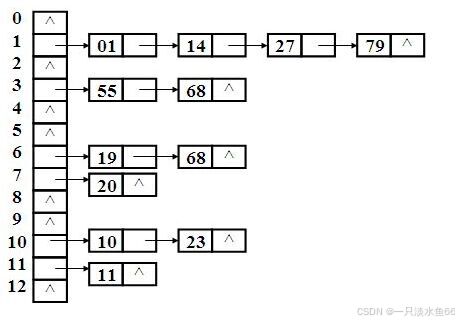
链地址法(Separate Chaining)是一种用于处理哈希表中哈希冲突的常见策略。在哈希表中,当多个元素通过哈希函数映射到相同的索引位置时,链地址法能够有效地将这些元素组织在一起,避免冲突造成的元素丢失。
链地址法的工作原理:
哈希表结构:
哈希表的每个索引位置通常是一个指向链表(或其他数据结构,如树)的指针。这意味着每个索引位置可以存储多个元素。哈希插入:
当需要插入一个元素时,首先计算该元素的哈希值,找到对应的索引位置。如果该位置为空,直接将元素放入;如果该位置已经有元素,则将新元素添加到该索引位置对应的链表中(可以是链表的头部或尾部,具体实现可以不同)。哈希查找:
查找某个元素时,同样计算元素的哈希值,并找到对应的索引位置。在该位置的链表中进行线性搜索,查找是否存在与目标元素相匹配的值。哈希删除:
删除元素时,先找到元素的哈希值对应的链表,然后在链表中进行查找,如果找到匹配的元素,就将其从链表中移除。链地址法的优缺点:
优点:
实现简单,逻辑清晰,能够有效地处理冲突而不影响其他元素的存储。不需要在插入时重新计算和移动其他元素,扩展性较好。适合负载因子较高的情况,只要存储的链表不会过长,性能依然可以得到保证。缺点:
在负载因子很高的情况下,链表长度可能增加,查找性能可能退化到O(n)。每个索引位置可能占用额外的存储空间,特别是在链表较长时,内存使用不是很高效。需要处理内存管理(如动态分配和释放),可能增加实现的复杂性。总结:
链地址法是一种有效的哈希冲突解决策略,能够通过将冲突元素存储在链表中来维持哈希表的高效性。其简单易实现的特性使其在许多实际应用中得到了广泛的采用,尤其是在预期有较多冲突的情况下,能够保持较好的性能。
代码模拟实现链地址法(哈希桶)
public class HashBuck { static class Node { public int key; public int value; public Node next; public Node(int key,int val) { this.key = key; this.value = val; } } public Node[] elem; public int usedSize; public HashBuck() { this.elem = new Node[10]; } //往哈希桶里面放元素 public void put(int key,int val) { Node node = new Node(key,val); int tmp = key % this.elem.length; Node cur = this.elem[tmp]; while(cur.next != null) { if(cur.value == val) { cur.value = val; return; } cur = cur.next; } cur.next = node; this.usedSize++; //负载因子超过了0.75,需要扩容 if(loadFactor() >= 0.75) { //调用扩容函数 resize(); } } //扩容函数 private void resize() { Node[] tmpArr = new Node[this.elem.length*2]; for (int i = 0; i < this.elem.length; i++) { Node cur = this.elem[i]; while(cur != null) { //记录cur.next的位置 Node curNext = cur.next; int newIndex = cur.key / tmpArr.length; //头插法 cur.next = tmpArr[newIndex]; tmpArr[newIndex] = cur; cur = curNext; } } this.elem = tmpArr; } //求出当前负载因子 private double loadFactor() { return this.usedSize*1.0 / this.elem.length; } //给定一个key值在哈希桶里面找到并返回其value值 public int get(int key) { int index = key % this.elem.length; Node cur = this.elem[index]; while(cur != null) { if(cur.key == key) { return cur.value; } cur = cur.next; } return -1; }}