基于整数规划的工件决策问题
ps:第四题要结合概率论,还需要优化
第三题就是第二题的加深版本,比较好些
第一问还会补充一些关于分阶段的抽样检测策略,提供检测次数尽可能少的抽样检测方案。
针对问题一, 我们首先对抽样检测方法进行建模,二项分布通常用于描述大样本的抽样概率分布,并且针对不同的商品数和信度,我们计算出了不同的样品检测数量,用尽可能少的检测样品量,得出检测结果,在 95%的信度下认定零配件次品率超过XXX标称值, 则拒收这批零配件。在 90%的信度下认定零配件次品率不超过XXX标称值, 则接受这批零配件。
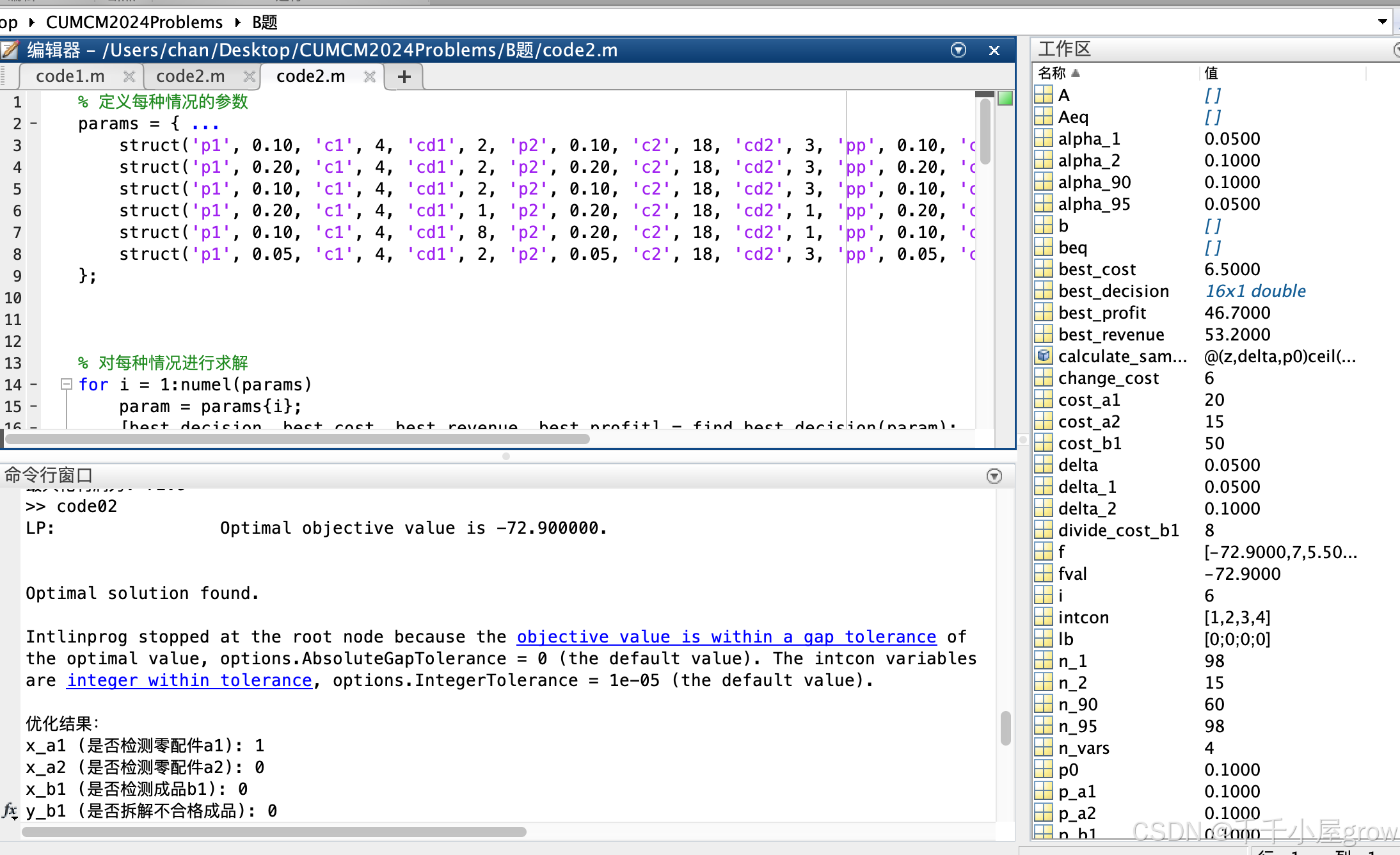
针对问题二, 我们考虑用整数规划来量化每一个决策过程,通过将目标函数定为最大化利润,将成本量化为购买成本、检测成本、装配成本、拆解成本、调换成本,设定约束条件后,我们得到了这几种情况下的最佳决策。
针对问题三, 与问题二类似,我们考虑用整数规划来量化每一个决策过程,并且加入更多的决策间的博弈,通过将目标函数定为最大化利润,将成本量化为购买成本、检测成本、装配成本、拆解成本、调换成本,设定约束条件后,我们得到了最佳决策。
生产过程中的决策问题
某企业生产某种畅销的电子产品,需要分别购买两种零配件(零配件 1 和零配件 2),在企业将两个零配件装配成成品。在装配的成品中,只要其中一个零配件不合格, 则成品一定不合格; 如果两个零配件均合格,装配出的成品也不一定合格。对于不合格成品,企业可以选择报废, 或者对其进行拆解,拆解过程不会对零配件造成损坏, 但需要花费拆解费用。
问题 1 供应商声称一批零配件(零配件 1 或零配件 2)的次品率不会超过某个标称值。企业准备采用抽样检测方法决定是否接收从供应商购买的这批零配件,检测费用由企业自行承担。请为企业设计检测次数尽可能少的抽样检测方案。
如果标称值为 10%, 根据你们的抽样检测方案,针对以下两种情形,分别给出具体结果:
(1) 在 95%的信度下认定零配件次品率超过标称值, 则拒收这批零配件;
(2) 在 90%的信度下认定零配件次品率不超过标称值, 则接收这批零配件。
二项分布(Binomial Distribution)是概率论中常见的离散概率分布,描述了在一系列独立重复的随机试验中,成功事件发生的次数的概率分布。在抽样检测中,二项分布被广泛应用于描述二元结果的概率分布情况。
二项分布的概率质量函数:
二项分布的概率质量函数可以表示为:
其中,n 表示试验的次数,k 表示成功事件发生的次数,p 表示单次试验成功的概率。
抽样检测中的应用:
在抽样检测中,我们经常需要进行二元结果的判断,比如产品质量合格与否、病人患病与否等。通过二项分布,我们可以计算在一定样本量下,出现特定结果的概率,从而进行统计推断和决策制定。
样本量与置信水平:
在抽样检测中,样本量的大小和置信水平直接影响着检测的准确性。通过二项分布,我们可以计算在给定置信水平下,需要的样本量,以确保检测结果的可靠性和代表性。
实际应用场景:
二项分布在工程、医学、经济等领域的抽样检测中发挥着重要作用。通过对二项分布的理解和应用,我们能够更准确地评估风险、制定决策,并为实际问题提供科学的分析依据。
一)在95%的信度下认定零配件次品率超过标称值, 则拒收这批零配件;
在 95%的信度下认定零配件次品率超过标称值, 则拒收这批零配件
在给定N个货品、α=95%的置信度的情况下,我们可以使用二项分布的抽样公式来计算所需的样本量和临界值。
样本量的计算公式如下:
[ n = \dfrac{Z^2 \cdot p \cdot (1-p)}{E^2} ]
其中, n是样本量;Z(α/2)是置信水平对应的Z值;p是预期的不合格率;E是允许的误差。
在这里,我们假设置信度为95%,对应的Z值为1.96(查表得到),预期的不合格率p为-0.1.
其中,根据工厂零部件具体的产品类型、行业标准和质量要求,允许误差E通常有着不同的数值。一般来说,工厂零部件的抽样检测会设定较小的允许误差,以确保产品质量符合要求。
一些常见的参考值是:
? =0.01: 如果产品质量要求非常高,对于零部件的质量控制非常严格,允许的误差可以设置为较小的值,如0.01。
?=0.05: 在一般情况下,允许的误差常常设定为0.05,这是一个常见的选择,能够平衡精度和实际情况。
?=0.1: 对于某些零部件,如果质量要求相对宽松,且对于生产效率有一定要求,允许的误差可能会设定为0.1。
允许的误差E需要根据具体情况给出,这里我们E值设置为0.05,适用于大多数情况。
临界值可以通过二项分布的临界值函数来计算,公式如下:
[ x_{\text{critical}} = \text{binoinv}(0.95, n, p) ]
其中,n为样本量,p为不合格率0.1.
这里的 ( x_{\text{critical}} ) 是样本中不合格品的临界值。
如果抽样得到的次品数量x 大于 ( x_{\text{critical}} ),则拒绝这批零配件。
问题 2 已知两种零配件和成品次品率,请为企业生产过程的各个阶段作出决策:
(1) 对零配件(零配件 1 和/或零配件 2) 是否进行检测,如果对某种零配件不检测, 这种零配件将直接进入到装配环节;否则将检测出的不合格零配件丢弃;
(2) 对装配好的每一件成品是否进行检测,如果不检测,装配后的成品直接进入到市场;否则只有检测合格的成品进入到市场;
(3) 对检测出的不合格成品是否进行拆解,如果不拆解,直接将不合格成品丢弃; 否则对拆解后的零配件, 重复步骤(1)和步骤(2);
(4) 对用户购买的不合格品,企业将无条件予以调换,并产生一定的调换损失(如物流成本、 企业信誉等)。 对退回的不合格品, 重复步骤(3)。
请根据你们所做的决策,对表 1 中的情形给出具体的决策方案,并给出决策的依据及相应的指标结果。
零配件a1,次品率p_a1=0.1,购买单价为cost_a1=4,检测成本test_cost_a1 = 2
零配件a2,次品率p_a2=0.1,购买单价为cost_a2=18,检测成本test_cost_a2 =3;
成品b1由a1和a2组成,次品率为p_b1,装配成本为cost_b1=18,检测成本test_b1 =3,b1的拆解费用divide_cost_b1=5;
市场售价为profit=56;如果用户购买的不合格品为无条件调换,成本为change_cost=6;
整数规划(Integer Programming)是一种数学优化技术,用于处理决策变量必须为整数的优化问题。在实际应用中,许多问题需要在决策变量为整数时进行优化,如生产调度、资源分配等领域。
整数规划模型在实际问题中的应用广泛,例如生产计划、运输优化等方面。通过整数规划,可以在满足约束条件的前提下,找到最优的决策方案,从而提高效率、降低成本,并优化资源利用。
整数规划模型的优势在于能够处理离散决策问题,通过对整数变量的限制,使得模型更符合实际情况。在决策过程中,整数规划模型对于优化问题的求解提供了有力的工具,为管理者提供了科学的决策支持。
在这里,我们采用整数规划来描述我们的决策过程,并将目标函数设为最大化利润
决策变量定义:
x₁ ∈ {0,1} : 是否检测零配件a1
x₂ ∈ {0,1} : 是否检测零配件a2
x₃ ∈ {0,1} : 是否检测成品b1
x₄ ∈ {0,1} : 是否拆解不合格成品
p_a1, p_a2 : 零配件a1和a2的次品率
p_b1 : 成品b1的次品率
cost_a1, cost_a2 : 零配件a1和a2的购买单价
test_cost_a1, test_cost_a2 : 零配件a1和a2的检测成本
cost_b1 : 成品b1的装配成本
test_b1 : 成品b1的检测成本
divide_cost_b1 : 成品b1的拆解费用
profit : 成品b1的市场售价
change_cost : 不合格品调换成本
max Z = R - (C_a + C_t + C_b + C_d + C_c)
R为预期收入,C_a, C_t, C_b, C_d, C_c 分别为零配件成本、检测成本、装配成本、拆解成本和调换成本。
R = profit * (1 - p_b1) * [1 - x₃p_b1 + x₃p_b1(1 - p_b1)]
C_a = cost_a1 + cost_a2
略
模型说明
预期收入R考虑了成品的次品率和是否进行成品检测。当不检测成品时(x₃ = 0),预期合格品比例为(1 - p_b1);当检测成品时(x₃ = 1),预期合格品比例为(1 - p_b1)²。
零配件成本C_a假设每个成品b1由一个a1和一个a2组成。
检测成本C_t根据是否检测各个组件来计算。
拆解成本C_d考虑了两种情况:检测出的不合格成品(x₃p_b1)和用户退回的不合格品((1 - x₃p_b1)p_b1)。
调换成本C_c假设所有进入市场的不合格品都会被用户发现并要求调换。

https://docs.qq.com/doc/DVXhKbFhpcHBXZGJJ