独家思维导图！让你秒懂李宏毅2020深度学习（三）——深度学习基础（神经网络和反向传播部分）

长文预警！！！前面两篇文章主要介绍了李宏毅视频中的机器学习部分，从这篇文章开始，我将介绍李宏毅视频中的深度学习部分，难度又将提升一个档次，大家一起加油鸭！本篇内容融合了李宏毅深度学习基础部分的多项知识，顺序根据博主的理解进行了些许调整，旨在能让大家更清晰的理解，有啥理解不对的地方欢迎大家批评指正！

前两篇文章传送门：
独家思维导图！让你秒懂李宏毅2020机器学习（一）—— Regression回归
独家思维导图！让你秒懂李宏毅2020机器学习（二）—— Classification分类

Up and downs of Deep Learning

李老师首先给我们介绍了深度学习的起起伏伏（发展史）这里引用网上的一张图片：

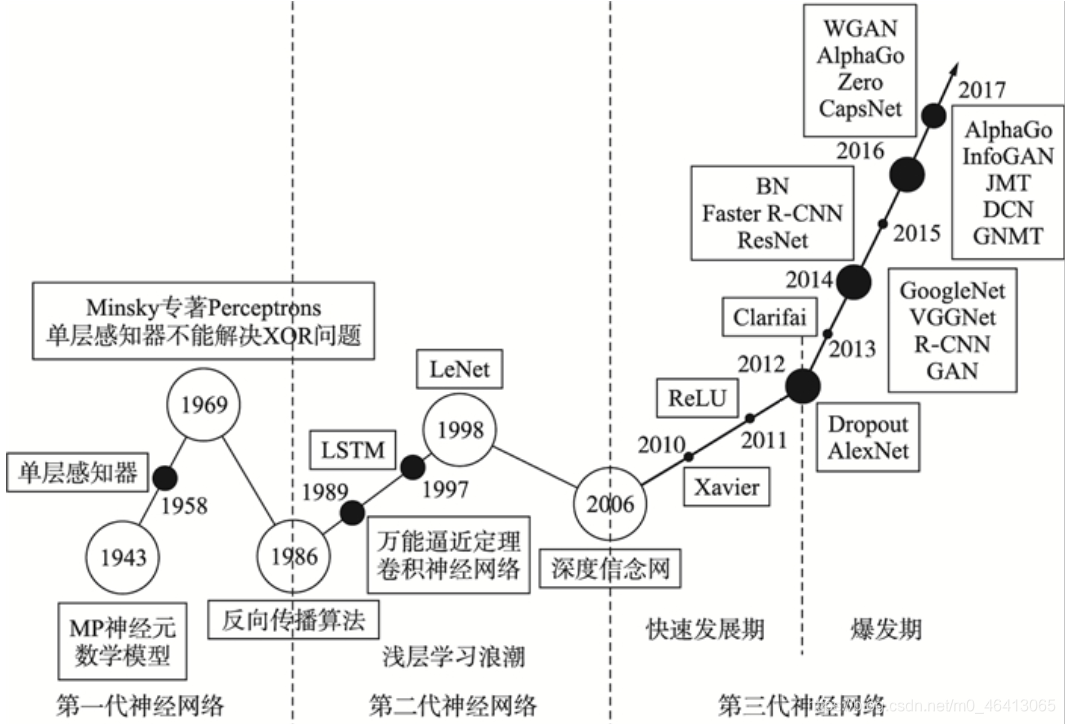
• 1958：Perceptron(linear model)，感知机的提出和Logistic Regression类似，只是少了sigmoid的部分1969：Perceptron has limitation，from MIT
• 1980s：Multi-layer Perceptron，多层感知机和今天的DNN很像
• 1986：Backpropagation，反向传播Hinton propose的Backpropagation 存在problem：通常超过3个layer的neural network，就train不出好的结果
• 1989: 1 hidden layer is “good enough”，why deep？ 有⼈提出⼀个理论：只要neural network有⼀个hidden layer，它就可以model出任何的function，所以根本没有必要叠加很多个hidden layer，所以Multi-layer Perceptron的⽅法⼜坏掉了，这段时间Multi-layer Perceptron这个东西是受到抵制的
• 2006：RBM initialization(breakthrough)：Restricted Boltzmann Machine，受限玻尔兹曼机 Deep learning -> another Multi-layer Perceptron
  在当时看来，它们的不同之处在于在做gradient descent的时候选取初始值的⽅法如果是⽤RBM，那就是Deep
  learning；如果没有⽤RBM，就是传统的Multi-layer Perceptron那实际上呢，RBM⽤的不是neural network base的⽅法，⽽是graphical model，后来⼤家试验得多了发现RBM并没有什么太⼤的帮助，因此现在基本上没有⼈使⽤RBM做initialization了
  RBM最⼤的贡献是，它让⼤家重新对Deep learning这个model有了兴趣(⽯头汤的故事)
• 2009：GPU加速的发现
• 2011：start to be popular in speech recognition，语⾳识别领域
• 2012：win ILSVRC image competition，Deep learning开始在图像领域流⾏开来

联系前面的机器学习，深度学习的三个步骤跟机器学习基本一致，只不过第一步找Function变成了找Neural Network

因此，理解Deep Learning在Mechine Learning 上的一大改进就从理解Deep Learning的fuction——Neural Network开始吧!

Neural Network

在这里我们先不按照李老师的讲课内容普及一些东西：
纵观神经网络的发展：（是不是发现跟深度学习的发展神似呢）

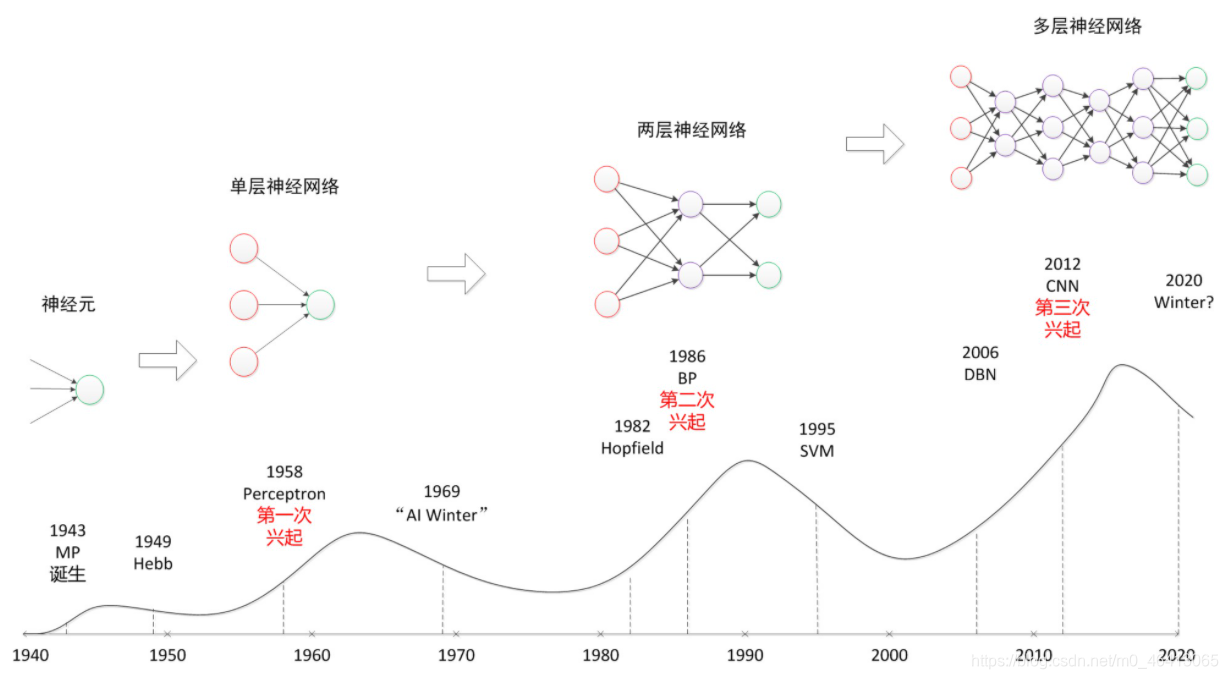
可见，神经网络是深度学习不可缺少的一部分。

在按历史进程介绍神经网络之前，我们先来熟悉下常见的几种激活函数
我总结为思维导图如下：

M-P神经元模型

结构

1943年，McCulloch和Pitts构成了一种人工神经元模型，也就是我们现在经常用到的“M-P神经元模型”，如下图所示：

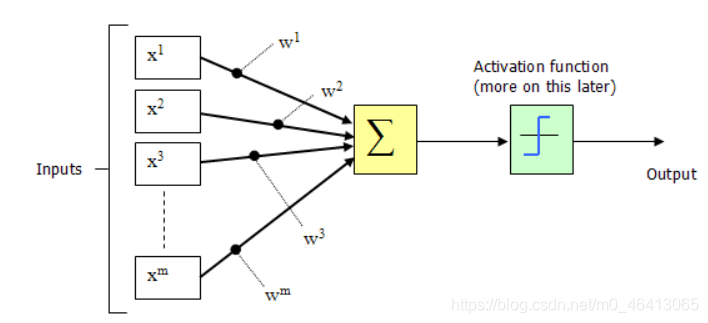
从上图M-P神经元模型可以看出，神经元的输出：

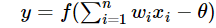
也可以写成这样：

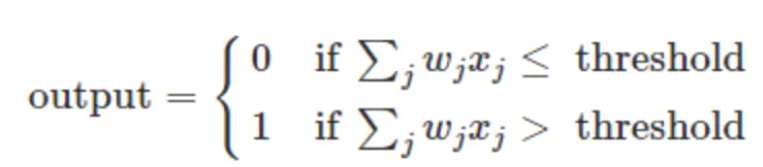
其中θ为我们之前提到的神经元的激活阈值，函数f(⋅)也被称为是激活函数。如上图所示，函数f(⋅)可以用一个阶跃方程表示，大于阈值激活；否则则抑制。但是这样有点太粗暴，因为阶跃函数不光滑，不连续，不可导，因此在后面的探索中我们进化出了几种较好的常用激活函数，我们在之后会详细介绍。

以下内容大部分来自博客
下图是一个典型的神经元模型：包含有3个输入，1个输出，以及2个计算功能。
　　注意中间的箭头线。这些线称为“连接”。每个上有一个“权值”。

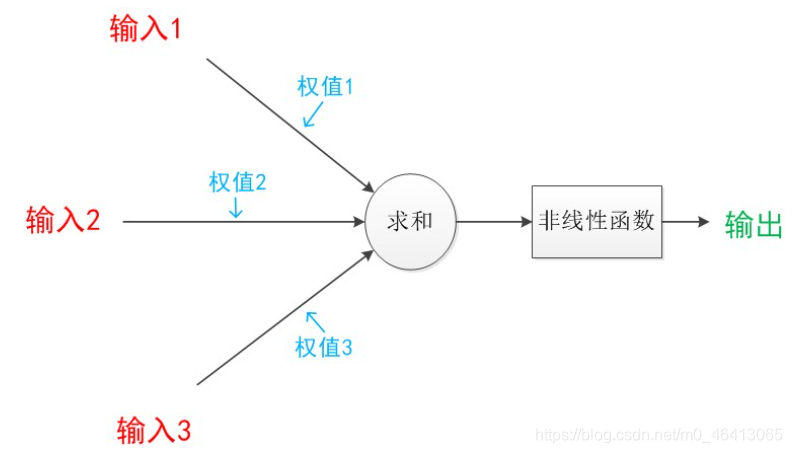
连接是神经元中最重要的东西。每一个连接上都有一个权重。
　　一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。
　　我们使用a来表示输入，用w来表示权值。一个表示连接的有向箭头可以这样理解：在初端，传递的信号大小仍然是a，端中间有加权参数w，经过这个加权后的信号会变成aw，因此在连接的末端，信号的大小就变成了aw。
　　在其他绘图模型里，有向箭头可能表示的是值的不变传递。而在神经元模型里，每个有向箭头表示的是值的加权传递。

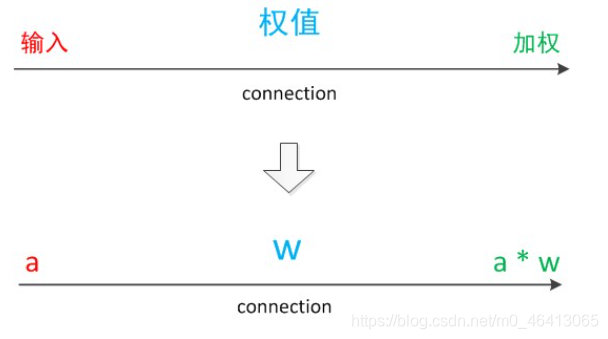
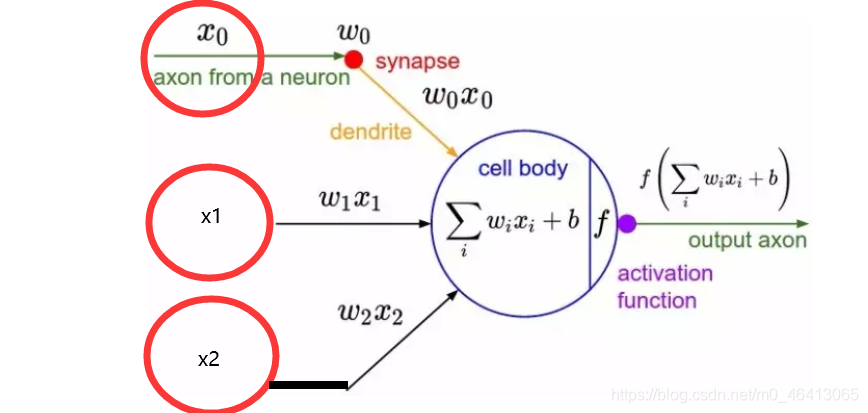
如果我们将神经元图中的所有变量用符号表示，并且写出输出的计算公式的话，就是下图。

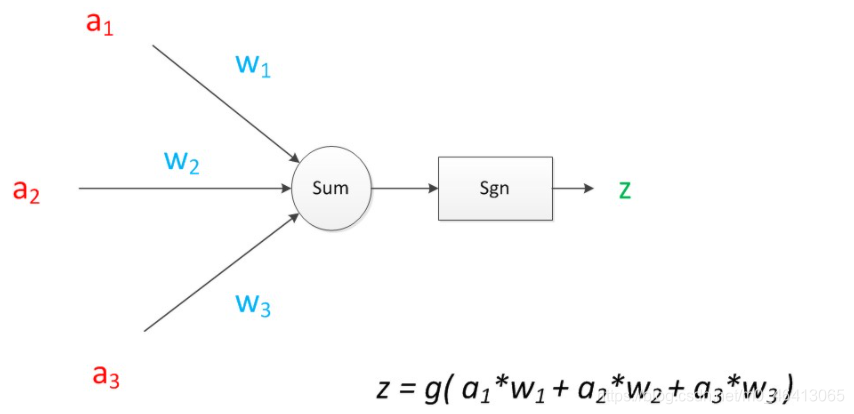
可见z是在输入和权值的线性加权和叠加了一个函数g的值。在MP模型里，函数g是sgn函数，也就是取符号函数。这个函数当输入大于0时，输出1，否则输出0。

下面对神经元模型的图进行一些扩展。首先将sum函数与sgn函数合并到一个圆圈里，代表神经元的内部计算。其次，把输入a与输出z写到连接线的左上方，便于后面画复杂的网络。最后说明，一个神经元可以引出多个代表输出的有向箭头，但值都是一样的。

神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果，并传递到下一层。

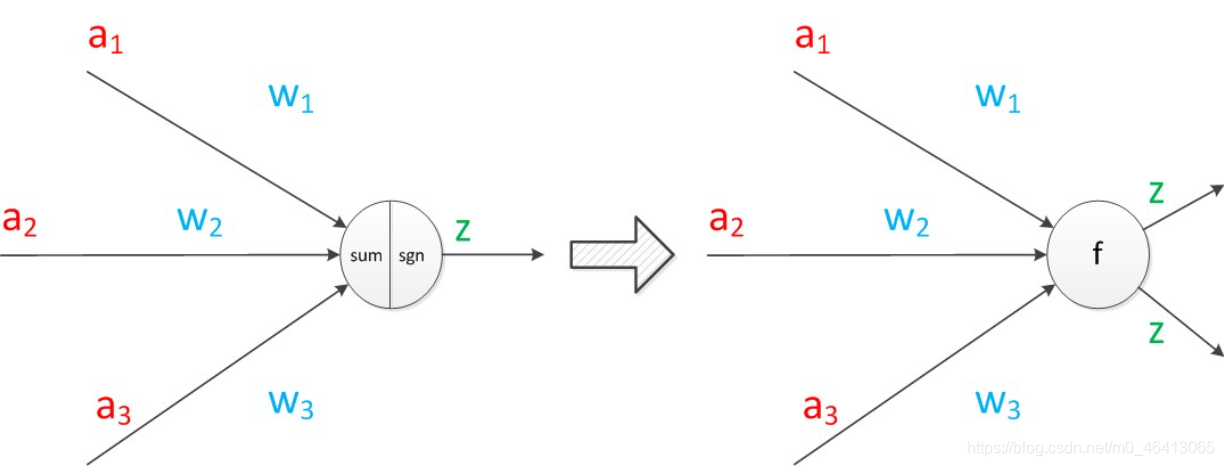
神经元扩展

当我们用“神经元”组成网络以后，描述网络中的某个“神经元”时，我们更多地会用“单元”（unit）来指代。同时由于神经网络的表现形式是一个有向图，有时也会用“节点”（node）来表达同样的意思。

效果

神经元模型的使用可以这样理解：
　　我们有一个数据，称之为样本。样本有四个属性，其中三个属性已知，一个属性未知。我们需要做的就是通过三个已知属性预测未知属性。
　　具体办法就是使用神经元的公式进行计算。三个已知属性的值是a1，a2，a3，未知属性的值是z。z可以通过公式计算出来。
　　这里，已知的属性称之为特征，未知的属性称之为目标。假设特征与目标之间确实是线性关系，并且我们已经得到表示这个关系的权值w1，w2，w3。那么，我们就可以通过神经元模型预测新样本的目标。

影响

1943年发布的MP模型，虽然简单，但已经建立了神经网络大厦的地基。但是，MP模型中，权重的值都是预先设置的，因此不能学习。
　　1949年心理学家Hebb提出了Hebb学习率，认为人脑神经细胞的突触（也就是连接）上的强度上可以变化的。于是计算科学家们开始考虑用调整权值的方法来让机器学习。这为后面的学习算法奠定了基础。

单层感知机模型(单层神经网络)

结构

从激活函数跳回来，刚刚说到1943年提出了神经元（MP模型）
在原来MP模型的“输入”位置添加神经元节点，标志其为“输入单元”。其余不变，于是就得到了1958年的单层感知机模型，这就是单层神经网络。

在“感知器”中，有两个层次。分别是输入层和输出层。输入层里的“输入单元”只负责传输数据，不做计算。输出层里的“输出单元”则需要对前面一层的输入进行计算。
我们把需要计算的层次称之为“计算层”，并把拥有一个计算层的网络称之为“单层神经网络”。
假如我们要预测的目标不再是一个值，而是一个向量。那么可以在输出层再增加一个“输出单元”。

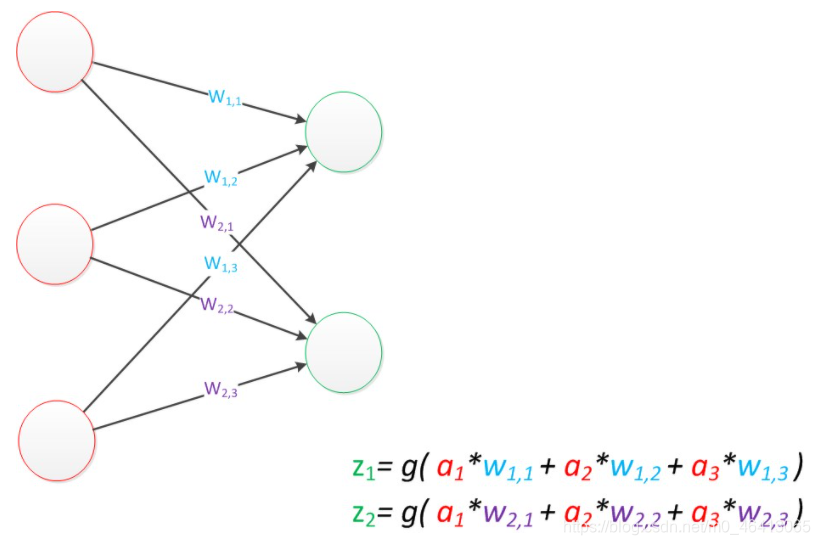
如果我们仔细看输出的计算公式，会发现这两个公式就是线性代数方程组。因此可以用矩阵乘法来表达这两个公式。
　　例如，输入的变量是[a1，a2，a3]T（代表由a1，a2，a3组成的列向量），用向量a来表示。方程的左边是[z1，z2]T，用向量z来表示。
　　系数则是矩阵W（2行3列的矩阵，排列形式与公式中的一样）。
　　于是，输出公式可以改写成：g(W * a) = z
　　这个公式就是神经网络中从前一层计算后一层的矩阵运算。

效果

与神经元模型不同，感知器中的权值是通过训练得到的。因此，根据以前的知识我们知道，感知器类似一个逻辑回归模型，可以做线性分类任务。
　　我们可以用决策分界来形象的表达分类的效果。决策分界就是在二维的数据平面中划出一条直线，当数据的维度是3维的时候，就是划出一个平面，当数据的维度是n维时，就是划出一个n-1维的超平面。
　　下图显示了在二维平面中划出决策分界的效果，也就是感知器的分类效果。

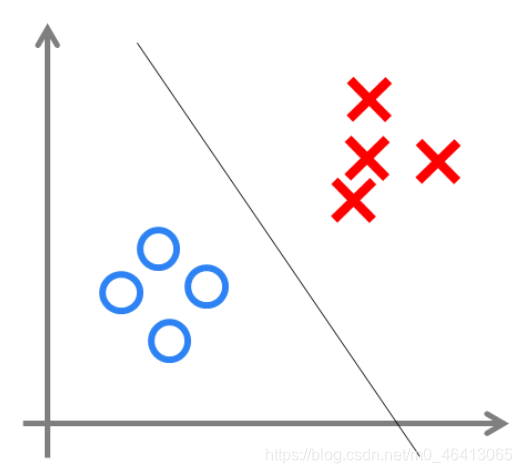
影响

感知器只能做简单的线性分类任务。但是当时的人们热情太过于高涨，并没有人清醒的认识到这点。于是，当人工智能领域的巨擘Minsky指出这点时，事态就发生了变化。

Minsky在1969年出版了一本叫《Perceptron》的书，里面用详细的数学证明了感知器的弱点，尤其是感知器对XOR（异或）这样的简单分类任务都无法解决。

Minsky认为，如果将计算层增加到两层，计算量则过大，而且没有有效的学习算法。所以，他认为研究更深层的网络是没有价值的。

由于Minsky的巨大影响力以及书中呈现的悲观态度，让很多学者和实验室纷纷放弃了神经网络的研究。神经网络的研究陷入了冰河期。这个时期又被称为“AI winter”。

接近10年以后，对于两层神经网络的研究才带来神经网络的复苏。

两层神经网络（多层感知器）

Minsky说过单层神经网络无法解决异或问题。但是当增加一个计算层以后，两层神经网络不仅可以解决异或问题，而且具有非常好的非线性分类效果。不过两层神经网络的计算是一个问题，没有一个较好的解法。

1986年，Rumelhar和Hinton等人提出了反向传播（Backpropagation，BP）算法，解决了两层神经网络所需要的复杂计算量问题，从而带动了业界使用两层神经网络研究的热潮。

结构

两层神经网络除了包含一个输入层，一个输出层以外，还增加了一个中间层。此时，中间层和输出层都是计算层。我们扩展上节的单层神经网络，在右边新加一个层次（只含有一个节点）。
　　现在，我们的权值矩阵增加到了两个，我们用上标来区分不同层次之间的变量。
　　例如ax(y)代表第y层的第x个节点。z1，z2变成了a1(2)，a2(2)。下图给出了a1(2)，a2(2)的计算公式。

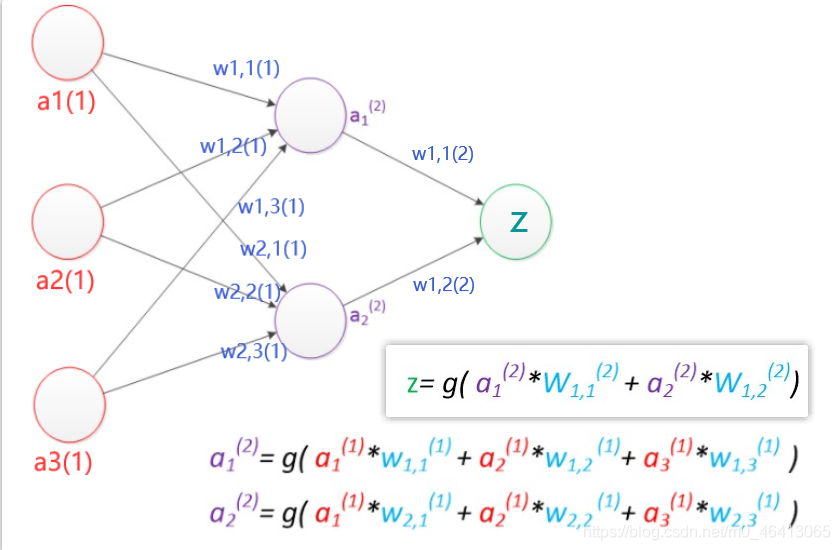
　　计算最终输出z的方式是利用了中间层的a1(2)，a2(2)和第二个权值矩阵计算得到的.

假设我们的预测目标是一个向量，那么与前面类似，只需要在“输出层”再增加节点即可。

我们使用向量和矩阵来表示层次中的变量。a(1)，a(2)，z是网络中传输的向量数据。W(1)和W(2)是网络的矩阵参数。如下图。

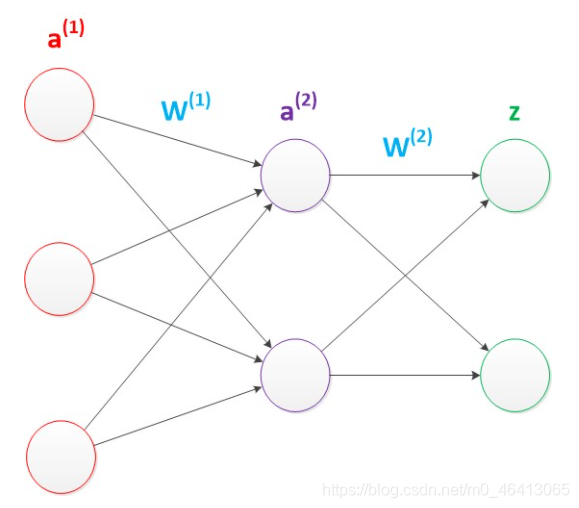
使用矩阵运算来表达整个计算公式的话如下：

g(W(1) * a(1)) = a(2);
g(W(2) * a(2)) = z;

由此可见，使用矩阵运算来表达是很简洁的，而且也不会受到节点数增多的影响（无论有多少节点参与运算，乘法两端都只有一个变量）。因此神经网络的教程中大量使用矩阵运算来描述。

需要说明的是，至今为止，我们对神经网络的结构图的讨论中都没有提到偏置节点（bias unit）。事实上，这些节点是默认存在的。它本质上是一个只含有存储功能，且存储值永远为1的单元。在神经网络的每个层次中，除了输出层以外，都会含有这样一个偏置单元。正如线性回归模型与逻辑回归模型中的一样。

偏置单元与后一层的所有节点都有连接，我们设这些参数值为向量b，称之为偏置。如下图。

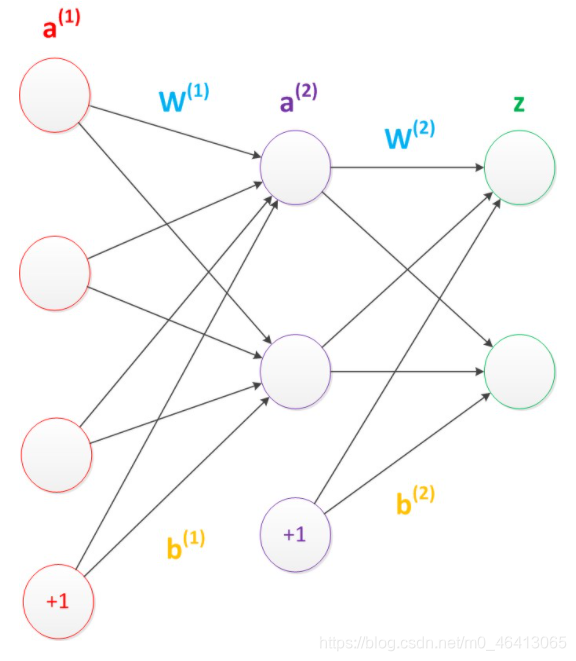
可以看出，偏置节点很好认，因为其没有输入（前一层中没有箭头指向它）。有些神经网络的结构图中会把偏置节点明显画出来，有些不会。一般情况下，我们都不会明确画出偏置节点。

考虑了偏置以后的一个神经网络的矩阵运算如下：

g(W(1) * a(1) + b(1)) = a(2);
g(W(2) * a(2) + b(2)) = z;

需要说明的是，在两层神经网络中，我们不再使用sgn函数作为函数g，而是使用平滑函数sigmoid作为函数g。我们把函数g也称作激活函数（active function）。p.s.刚刚介绍了激活函数的思维导图

事实上，神经网络的本质就是通过参数与激活函数来拟合特征与目标之间的真实函数关系。初学者可能认为画神经网络的结构图是为了在程序中实现这些圆圈与线，但在一个神经网络的程序中，既没有“线”这个对象，也没有“单元”这个对象。实现一个神经网络最需要的是线性代数库。

效果

与单层神经网络不同。理论证明，两层神经网络可以无限逼近任意连续函数。
　　
　　这是什么意思呢？也就是说，面对复杂的非线性分类任务，两层（带一个隐藏层）神经网络可以分类的很好。
　　
　　下面就是一个例子（此两图来自colah的博客），红色的线与蓝色的线代表数据。而红色区域和蓝色区域代表由神经网络划开的区域，两者的分界线就是决策分界。

可以看到，这个两层神经网络的决策分界是非常平滑的曲线，而且分类的很好。有趣的是，前面已经学到过，单层网络只能做线性分类任务。而两层神经网络中的后一层也是线性分类层，应该只能做线性分类任务。为什么两个线性分类任务结合就可以做非线性分类任务？

我们可以把输出层的决策分界单独拿出来看一下。就是下图。

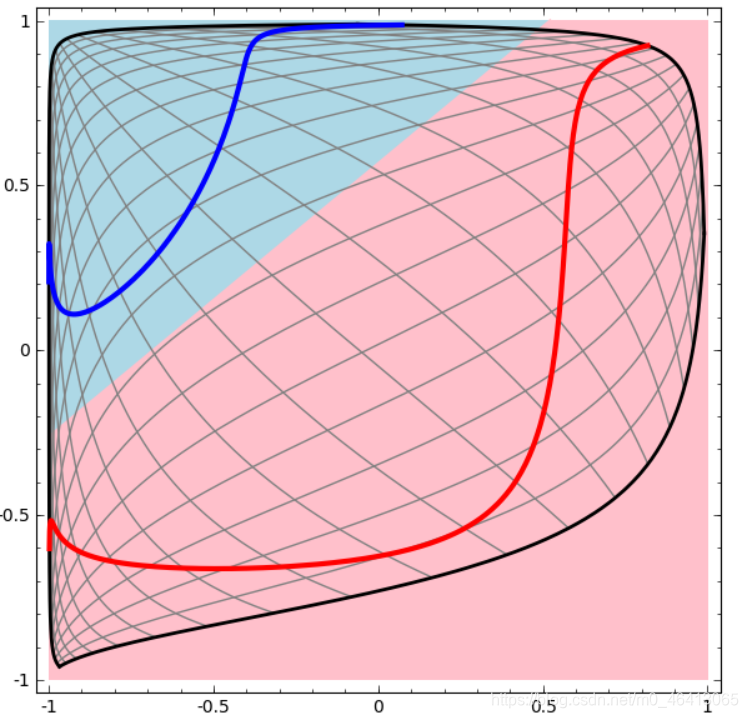
可以看到，输出层的决策分界仍然是直线。关键就是，从输入层到隐藏层时，数据发生了空间变换。也就是说，两层神经网络中，隐藏层对原始的数据进行了一个空间变换，使其可以被线性分类，然后输出层的决策分界划出了一个线性分类分界线，对其进行分类。

这样就导出了两层神经网络可以做非线性分类的关键–隐藏层。联想到我们一开始推导出的矩阵公式，我们知道，矩阵和向量相乘，本质上就是对向量的坐标空间进行一个变换。因此，隐藏层的参数矩阵的作用就是使得数据的原始坐标空间从线性不可分，转换成了线性可分。

两层神经网络通过两层的线性模型模拟了数据内真实的非线性函数。因此，多层的神经网络的本质就是复杂函数拟合。

下面来讨论一下隐藏层的节点数设计。在设计一个神经网络时，输入层的节点数需要与特征的维度匹配，输出层的节点数要与目标的维度匹配。而中间层的节点数，却是由设计者指定的。因此，“自由”把握在设计者的手中。但是，节点数设置的多少，却会影响到整个模型的效果。如何决定这个自由层的节点数呢？目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值，通过切换这几个值来看整个模型的预测效果，选择效果最好的值作为最终选择。这种方法又叫做Grid Search（网格搜索）。

训练

下面简单介绍一下两层神经网络的训练。
　　
　　在Rosenblat提出的感知器模型中，模型中的参数可以被训练，但是使用的方法较为简单，并没有使用目前机器学习中通用的方法，这导致其扩展性与适用性非常有限。从两层神经网络开始，神经网络的研究人员开始使用机器学习相关的技术进行神经网络的训练。例如用大量的数据（1000-10000左右），使用算法进行优化等等，从而使得模型训练可以获得性能与数据利用上的双重优势。

机器学习模型训练的目的，就是使得参数尽可能的与真实的模型逼近。具体做法是这样的。首先给所有参数赋上随机值。我们使用这些随机生成的参数值，来预测训练数据中的样本。样本的预测目标为yp，真实目标为y。那么，定义一个值loss，计算公式如下。

loss = (yp - y)2

这个值称之为损失（loss），我们的目标就是使对所有训练数据的损失和尽可能的小。

如果将先前的神经网络预测的矩阵公式带入到yp中（因为有z=yp），那么我们可以把损失写为关于参数（parameter）的函数，这个函数称之为损失函数（loss function）。下面的问题就是求：如何优化参数，能够让损失函数的值最小。

此时这个问题就被转化为一个优化问题。一个常用方法就是高等数学中的求导，但是这里的问题由于参数不止一个，求导后计算导数等于0的运算量很大，所以一般来说解决这个优化问题使用的是梯度下降算法。梯度下降算法每次计算参数在当前的梯度，然后让参数向着梯度的反方向前进一段距离，不断重复，直到梯度接近零时截止。一般这个时候，所有的参数恰好达到使损失函数达到一个最低值的状态。

在神经网络模型中，由于结构复杂，每次计算梯度的代价很大。因此还需要使用反向传播算法。反向传播算法是利用了神经网络的结构进行的计算。不一次计算所有参数的梯度，而是从后往前。首先计算输出层的梯度，然后是第二个参数矩阵的梯度，接着是中间层的梯度，再然后是第一个参数矩阵的梯度，最后是输入层的梯度。计算结束以后，所要的两个参数矩阵的梯度就都有了。

反向传播算法可以直观的理解为下图。梯度的计算从后往前，一层层反向传播。前缀E代表着相对导数的意思。

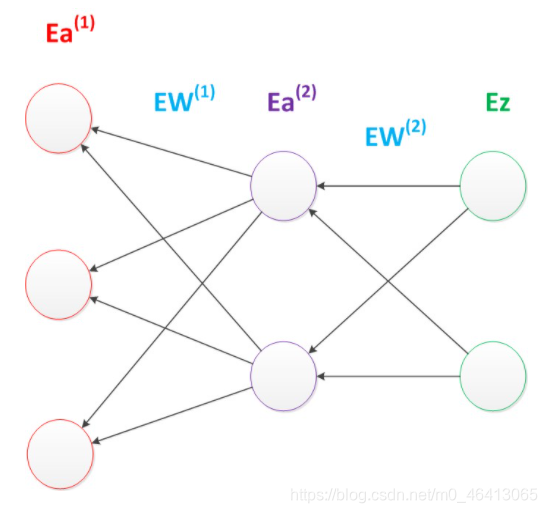
反向传播算法的启示是数学中的链式法则。在此需要说明的是，尽管早期神经网络的研究人员努力从生物学中得到启发，但从BP算法开始，研究者们更多地从数学上寻求问题的最优解。不再盲目模拟人脑网络是神经网络研究走向成熟的标志。正如科学家们可以从鸟类的飞行中得到启发，但没有必要一定要完全模拟鸟类的飞行方式，也能制造可以飞天的飞机。

优化问题只是训练中的一个部分。机器学习问题之所以称为学习问题，而不是优化问题，就是因为它不仅要求数据在训练集上求得一个较小的误差，在测试集上也要表现好。因为模型最终是要部署到没有见过训练数据的真实场景。提升模型在测试集上的预测效果的主题叫做泛化（generalization），相关方法被称作正则化（regularization）。神经网络中常用的泛化技术有权重衰减等。

影响

两层神经网络在多个地方的应用说明了其效用与价值。10年前困扰神经网络界的异或问题被轻松解决。神经网络在这个时候，已经可以发力于语音识别，图像识别，自动驾驶等多个领域。

历史总是惊人的相似，神经网络的学者们再次登上了《纽约时报》的专访。人们认为神经网络可以解决许多问题。就连娱乐界都开始受到了影响，当年的《终结者》电影中的阿诺都赶时髦地说一句：我的CPU是一个神经网络处理器，一个会学习的计算机。

但是神经网络仍然存在若干的问题：尽管使用了BP算法，一次神经网络的训练仍然耗时太久，而且困扰训练优化的一个问题就是局部最优解问题，这使得神经网络的优化较为困难。同时，隐藏层的节点数需要调参，这使得使用不太方便，工程和研究人员对此多有抱怨。

90年代中期，由Vapnik等人发明的SVM（Support Vector Machines，支持向量机）算法诞生，很快就在若干个方面体现出了对比神经网络的优势：无需调参；高效；全局最优解。基于以上种种理由，SVM迅速打败了神经网络算法成为主流。

Vladimir Vapnik

神经网络的研究再次陷入了冰河期。当时，只要你的论文中包含神经网络相关的字眼，非常容易被会议和期刊拒收，研究界那时对神经网络的不待见可想而知。

多层神经网络（深度学习）

p.s. 在这里只论述普通的多层神经网络。

2006年，Hinton在《Science》和相关期刊上发表了论文，首次提出了“深度信念网络”的概念。与传统的训练方式不同，“深度信念网络”有一个“预训练”（pre-training）的过程，这可以方便的让神经网络中的权值找到一个接近最优解的值，之后再使用“微调”(fine-tuning)技术来对整个网络进行优化训练。这两个技术的运用大幅度减少了训练多层神经网络的时间。他给多层神经网络相关的学习方法赋予了一个新名词–“深度学习”。
　　很快，深度学习在语音识别领域暂露头角。接着，2012年，深度学习技术又在图像识别领域大展拳脚。Hinton与他的学生在ImageNet竞赛中，用多层的卷积神经网络成功地对包含一千类别的一百万张图片进行了训练，取得了分类错误率15%的好成绩，这个成绩比第二名高了近11个百分点，充分证明了多层神经网络识别效果的优越性。
　　在这之后，关于深度神经网络的研究与应用不断涌现。

Geoffery Hinton

结构

我们延续两层神经网络的方式来设计一个多层神经网络。

在两层神经网络的输出层后面，继续添加层次。原来的输出层变成中间层，新加的层次成为新的输出层。

依照这样的方式不断添加，我们可以得到更多层的多层神经网络。公式推导的话其实跟两层神经网络类似，使用矩阵运算的话就仅仅是加一个公式而已。

在已知输入a(1)，参数W(1)，W(2)，W(3)的情况下，输出z的推导公式如下：

g(W(1) * a(1)) = a(2);
g(W(2) * a(2)) = a(3);
g(W(3) * a(3)) = z;

多层神经网络中，输出也是按照一层一层的方式来计算。从最外面的层开始，算出所有单元的值以后，再继续计算更深一层。只有当前层所有单元的值都计算完毕以后，才会算下一层。有点像计算向前不断推进的感觉。所以这个过程叫做“正向传播”。

下面讨论一下多层神经网络中的参数。

首先我们看第一张图，可以看出W(1)中有6个参数，W(2)中有4个参数，W(3)中有6个参数，所以整个神经网络中的参数有16个（这里我们不考虑偏置节点，下同）。

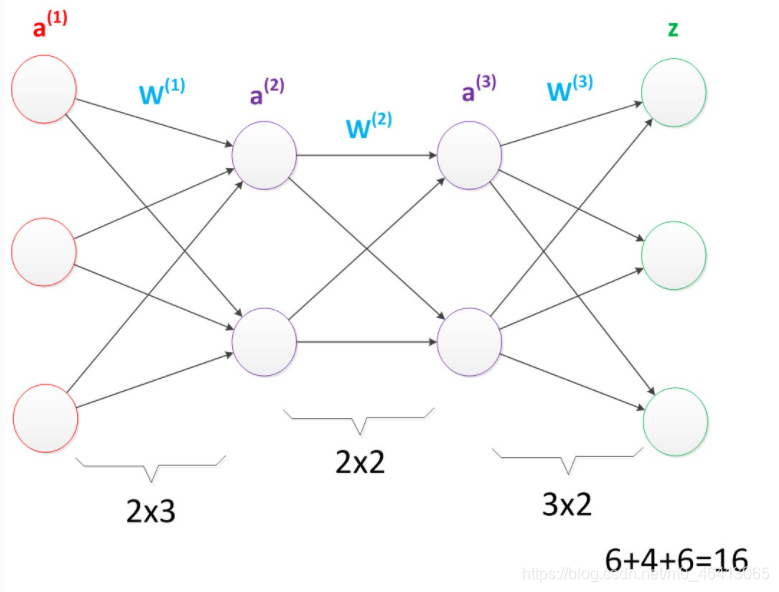多层神经网络（较少参数）

假设我们将中间层的节点数做一下调整。第一个中间层改为3个单元，第二个中间层改为4个单元。

经过调整以后，整个网络的参数变成了33个。

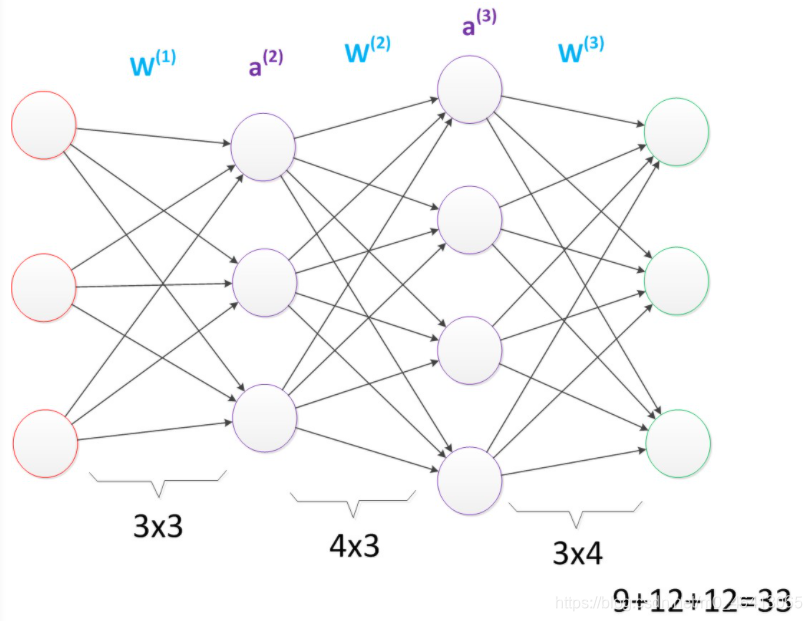
多层神经网络（较多参数）

虽然层数保持不变，但是第二个神经网络的参数数量却是第一个神经网络的接近两倍之多，从而带来了更好的表示（represention）能力。表示能力是多层神经网络的一个重要性质，下面会做介绍。

在参数一致的情况下，我们也可以获得一个“更深”的网络。

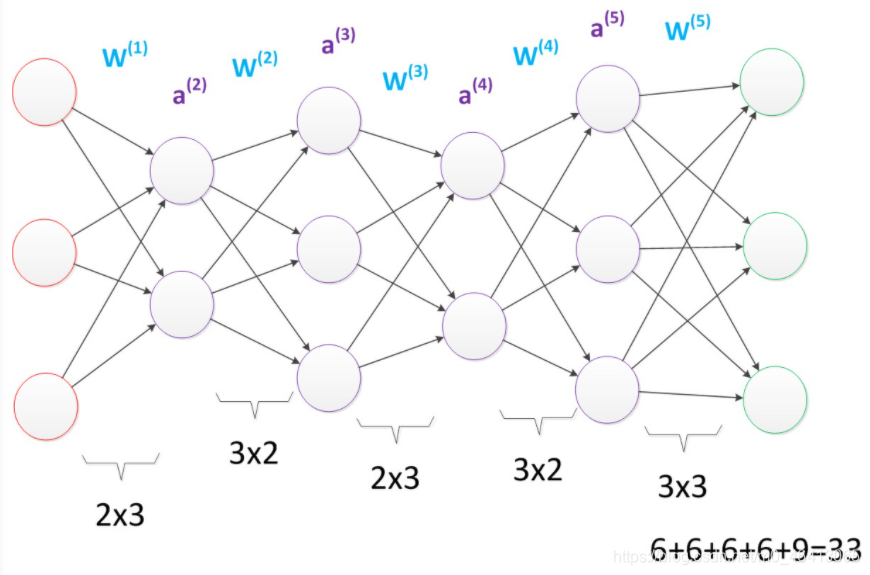
多层神经网络（更深的层次）

上图的网络中，虽然参数数量仍然是33，但却有4个中间层，是原来层数的接近两倍。这意味着一样的参数数量，可以用更深的层次去表达。

效果

与两层层神经网络不同。多层神经网络中的层数增加了很多。

增加更多的层次有什么好处？更深入的表示特征，以及更强的函数模拟能力。

更深入的表示特征可以这样理解，随着网络的层数增加，每一层对于前一层次的抽象表示更深入。在神经网络中，每一层神经元学习到的是前一层神经元值的更抽象的表示。例如第一个隐藏层学习到的是“边缘”的特征，第二个隐藏层学习到的是由“边缘”组成的“形状”的特征，第三个隐藏层学习到的是由“形状”组成的“图案”的特征，最后的隐藏层学习到的是由“图案”组成的“目标”的特征。通过抽取更抽象的特征来对事物进行区分，从而获得更好的区分与分类能力。

关于逐层特征学习的例子，可以参考下图。

多层神经网络（特征学习）

更强的函数模拟能力是由于随着层数的增加，整个网络的参数就越多。而神经网络其实本质就是模拟特征与目标之间的真实关系函数的方法，更多的参数意味着其模拟的函数可以更加的复杂，可以有更多的容量（capcity）去拟合真正的关系。

通过研究发现，在参数数量一样的情况下，更深的网络往往具有比浅层的网络更好的识别效率。这点也在ImageNet的多次大赛中得到了证实。从2012年起，每年获得ImageNet冠军的深度神经网络的层数逐年增加，2015年最好的方法GoogleNet是一个多达22层的神经网络。

在最新一届的ImageNet大赛上，目前拿到最好成绩的MSRA团队的方法使用的更是一个深达152层的网络！关于这个方法更多的信息有兴趣的可以查阅ImageNet网站。

训练

在单层神经网络时，我们使用的激活函数是sgn函数。到了两层神经网络时，我们使用的最多的是sigmoid函数。而到了多层神经网络时，通过一系列的研究发现，ReLU函数在训练多层神经网络时，更容易收敛，并且预测性能更好。因此，目前在深度学习中，最流行的非线性函数是ReLU函数。ReLU函数不是传统的非线性函数，而是分段线性函数。其表达式非常简单，就是y=max(x,0)。简而言之，在x大于0，输出就是输入，而在x小于0时，输出就保持为0。这种函数的设计启发来自于生物神经元对于激励的线性响应，以及当低于某个阈值后就不再响应的模拟。

在多层神经网络中，训练的主题仍然是优化和泛化。当使用足够强的计算芯片（例如GPU图形加速卡）时，梯度下降算法以及反向传播算法在多层神经网络中的训练中仍然工作的很好。目前学术界主要的研究既在于开发新的算法，也在于对这两个算法进行不断的优化，例如，增加了一种带动量因子（momentum）的梯度下降算法。

在深度学习中，泛化技术变的比以往更加的重要。这主要是因为神经网络的层数增加了，参数也增加了，表示能力大幅度增强，很容易出现过拟合现象。因此正则化技术就显得十分重要。目前，Dropout技术，以及数据扩容（Data-Augmentation）技术是目前使用的最多的正则化技术。

影响

目前，深度神经网络在人工智能界占据统治地位。但凡有关人工智能的产业报道，必然离不开深度学习。神经网络界当下的四位引领者除了前文所说的Ng，Hinton以外，还有CNN的发明人Yann Lecun，以及《Deep Learning》的作者Bengio。

前段时间一直对人工智能持谨慎态度的马斯克，搞了一个OpenAI项目，邀请Bengio作为高级顾问。马斯克认为，人工智能技术不应该掌握在大公司如Google，Facebook的手里，更应该作为一种开放技术，让所有人都可以参与研究。马斯克的这种精神值得让人敬佩。

Yann LeCun（左）和 Yoshua Bengio（右）

多层神经网络的研究仍在进行中。现在最为火热的研究技术包括RNN，LSTM等，研究方向则是图像理解方面。图像理解技术是给计算机一幅图片，让它用语言来表达这幅图片的意思。ImageNet竞赛也在不断召开，有更多的方法涌现出来，刷新以往的正确率。

总结

对上面的用下面两个图总结一下：

从单层神经网络，到两层神经网络，再到多层神经网络，下图说明了，随着网络层数的增加，以及激活函数的调整，神经网络所能拟合的决策分界平面的能力逐渐增强。

神经网络的发展背后的外在原因可以被总结为：更强的计算性能，更多的数据，以及更好的训练方法。

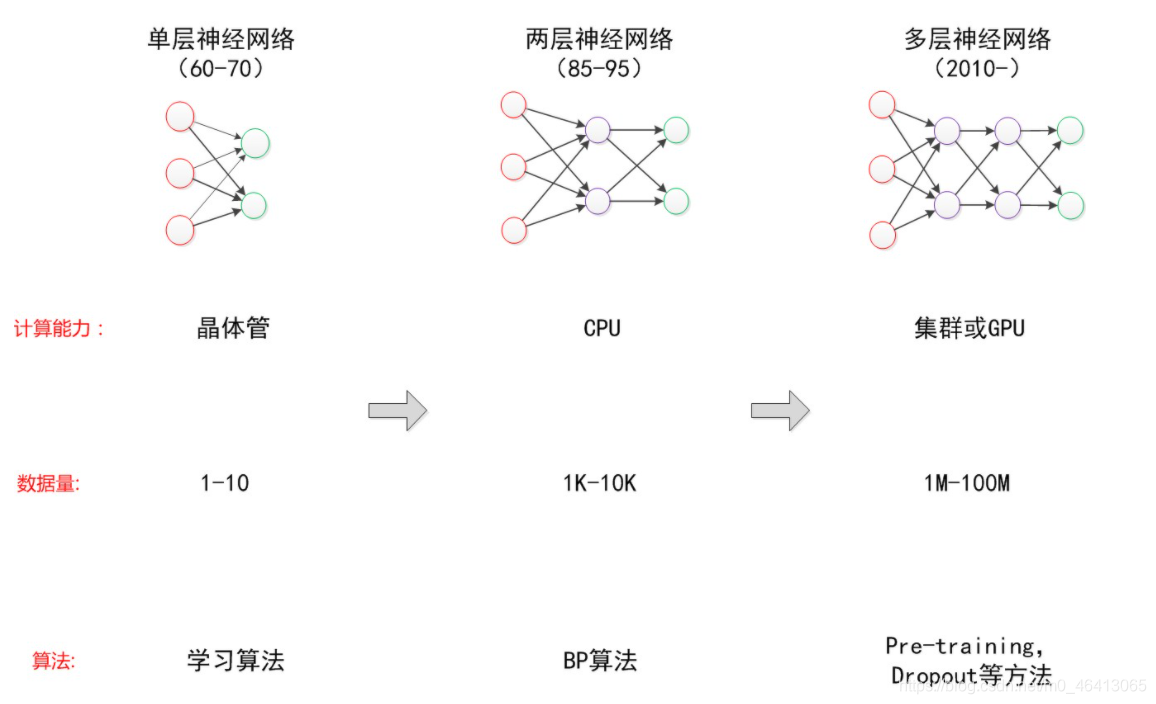
上面引用了博主目前看过写的最好的神经网络的文章内容，接下来回归李宏毅老师的课程：

李宏毅老师定义

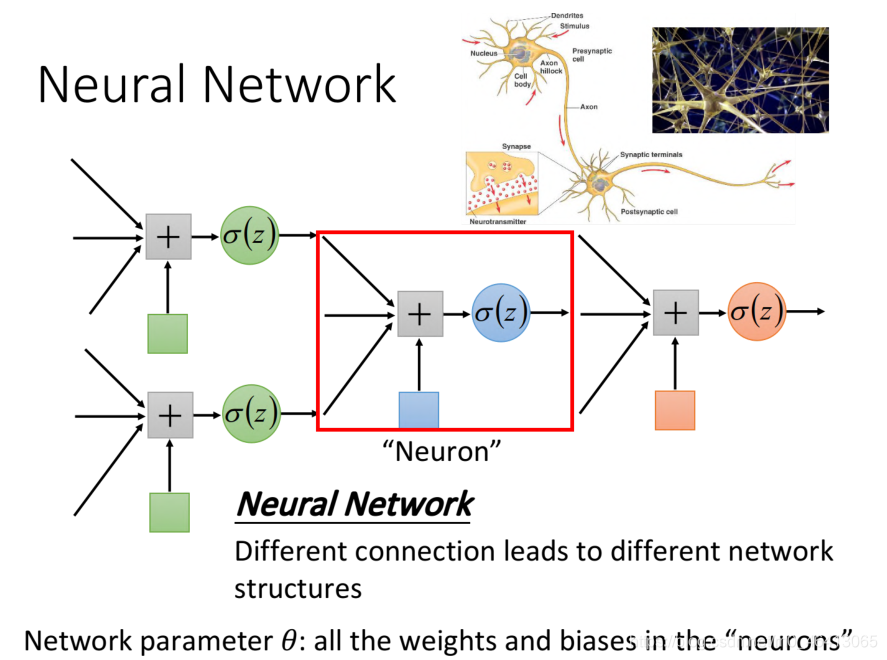
李老师把多个Logistic Regression前后connect在⼀起称之为neural network，⼀个Logistic Regression称之为neuron，neural network⾥的每⼀个Logistic Regression都有⾃⼰的weight和bias，这些weight和bias集合起来，就是这个network的parameter，我们⽤θ来描述

Fully Connect Feedforward Network(全连接前馈⽹络)

接下来李老师介绍了一种最常见的神经网络模型Fully Connect Feedforward Network(全连接前馈⽹络)

解释下名词

• Fully connected： layer和layer之间，所有的neuron都是两两连接
• Feedforward： 传递的⽅向是从layer 1->2->3，由前往后传，且没有反馈（feedback）
  （不会根据输出结果对输入结果的影响来进一步调整输出结果）

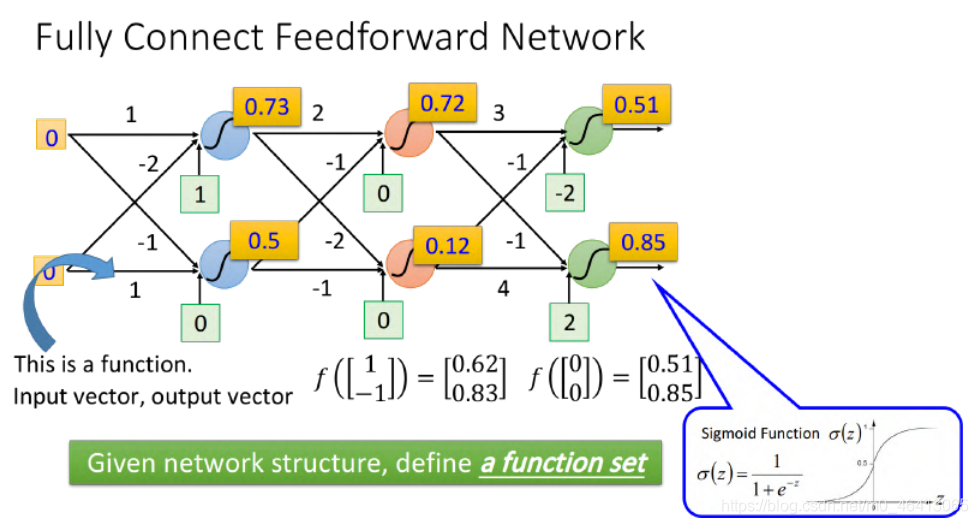
在这里李宏毅点明了神经网络和function的关系：

• ⼀个确定参数θ（weight和bias已知）的neural network是⼀个确定的function
• 一个未确定参数，但确定了结构的network structure是了⼀个function set(model)
  （设置不同的参数，它就变成了不同的function，把这些可能的function集合起来，我们就得到了⼀个function set）

好处是⽤neural network决定function set的时候，这个function set是⽐较⼤的，它包含了很多原来你做Logistic Regression、做linear Regression所没有办法包含的function

这种由神经网络确定的function的input是⼀个vector，output是另⼀个vector，这个vector⾥⾯放的是样本点的feature，vector的dimension就是feature的个数

下图中，每⼀排表⽰⼀个layer，每个layer⾥⾯的每⼀个球都代表⼀个neuron，layer和layer之间neuron是 两两互相连接 的，layer 1的neuron output会连接给layer 2的每⼀个neuron作为input

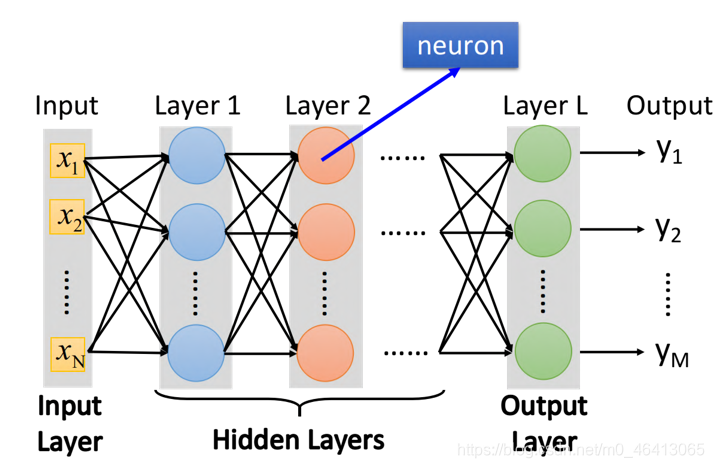
在这里我介绍一下关于神经网络的一些名词：

• input layer(输⼊层)：input某个feature的vector的地⽅
  (严格来说input layer其实不是⼀个layer，它跟其他layer不⼀样，不是由neuron所组成的)
• output layer(输出层)：最后那个layer L，由于它后⾯没有接其它东西了，所以它的output就是整个network的output
• hidden layer(隐藏层)：除输入层和输出层以外的其他层，对layer 1的每⼀个neuron来说，它的input就是input layer的每⼀个dimension
• DNN(Deep Neural Network)：有很多层layers的neural network

那所谓的deep，是什么意思呢？有很多层hidden layer，就叫做deep，具体的层数并没有规定，现在只要是neural network base的⽅法，都被称为Deep Learning，下图是⼀些model使⽤的hidden layers层数举例:

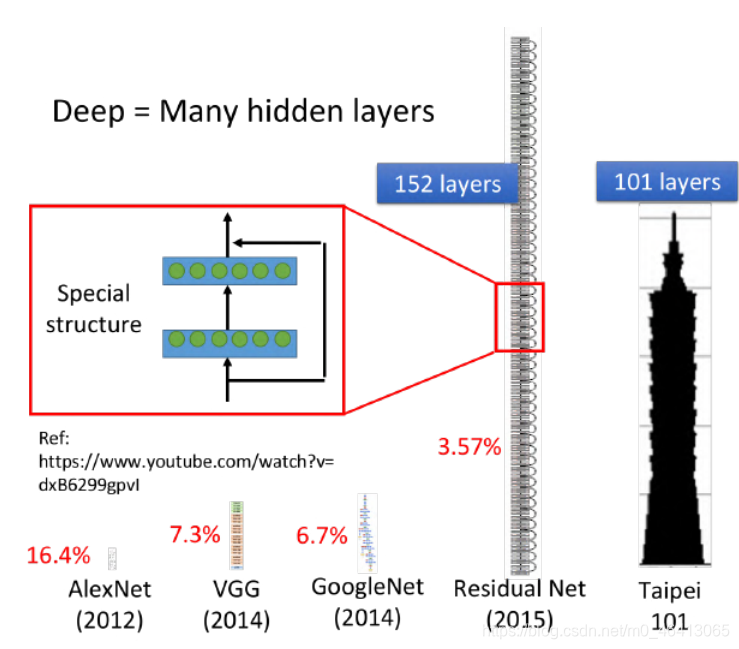
你会发现使⽤了152个hidden layers的Residual Net，它识别图像的准确率⽐⼈类还要⾼当然它不是使
⽤⼀般的Fully Connected Feedforward Network，它需要设计特殊的special structure才能训练这么深的network

激励函数

• activation function(激励函数)：在神经网络中，隐层和输出层节点的输入和输出之间具有函数关系，这个函数称为激励函数（Activation Function）。

这里就激励函数延申一下：

• 激励函数在神经网络的作用：将多个线性输入转换为非线性的关系。 不使用激励函数的话，神经网络的每层都只是做线性变换，多层输入叠加后也还是线性变换。因为线性模型的表达能力不够，激励函数可以引入非线性因素。

什么？还不够形象？博主在这里引用我看过最形象的解释：

无激励函数的神经网络

神经网络最简单的结构就是单输出的单层感知机，单层感知机只有输入层和输出层，分别代表了神经感受器和神经中枢。下图是一个只有2个输入单元和1个输出单元的简单单层感知机。图中x1、w2代表神经网络的输入神经元受到的刺激，w1、w2代表输入神经元和输出神经元间连接的紧密程度，b代表输出神经元的兴奋阈值，y为输出神经元的输出。我们使用该单层感知机划出一条线将平面分割开，如图所示：

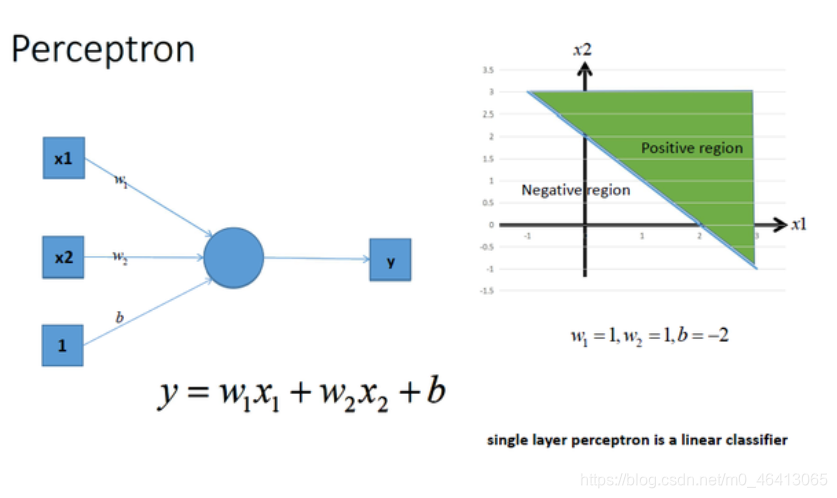
同理，我们也可以将多个感知机（注意，不是多层感知机）进行组合获得更强的平面分类能力，如图所示：

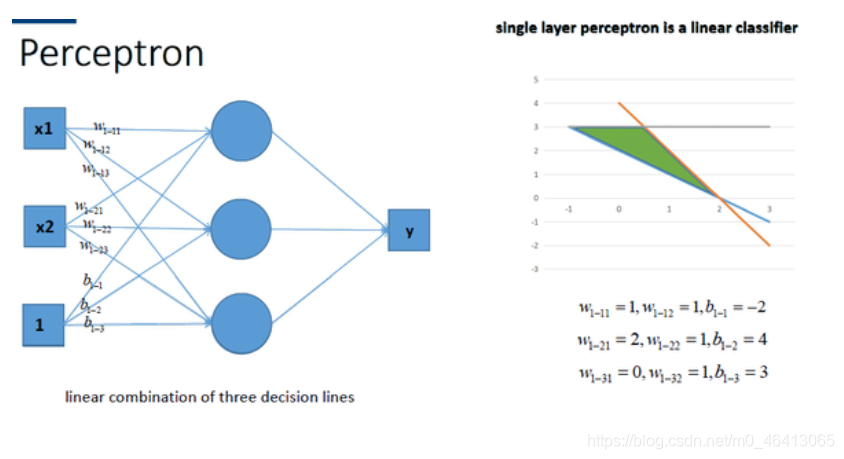
再看看包含一个隐层的多层感知机的情况，如图所示：

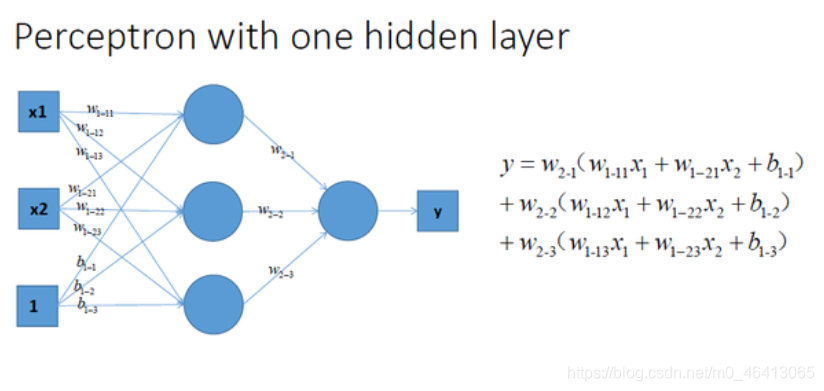
仔细看的话不难发现，上面三种没有激励函数的神经网络的输出是线性方程，其在用复杂的线性组合来逼近曲线。

有激励函数的神经网络

我们在神经网络每一层神经元做完线性变换以后，加上一个非线性激励函数对线性变换的结果进行转换，那么输出就是一个不折不扣的非线性函数了，如图所示：

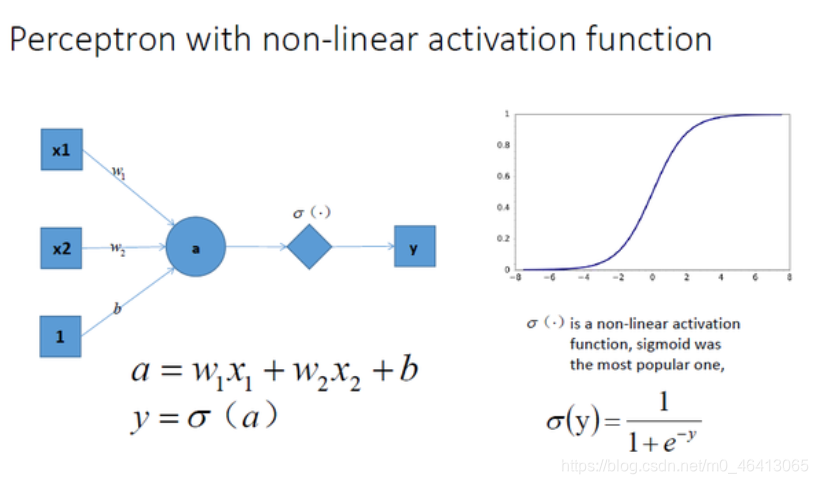
拓展到多层神经网络的情况, 更刚刚一样的结构, 加上非线性激励函数之后, 输出就变成了一个复杂的非线性函数了，如图所示：

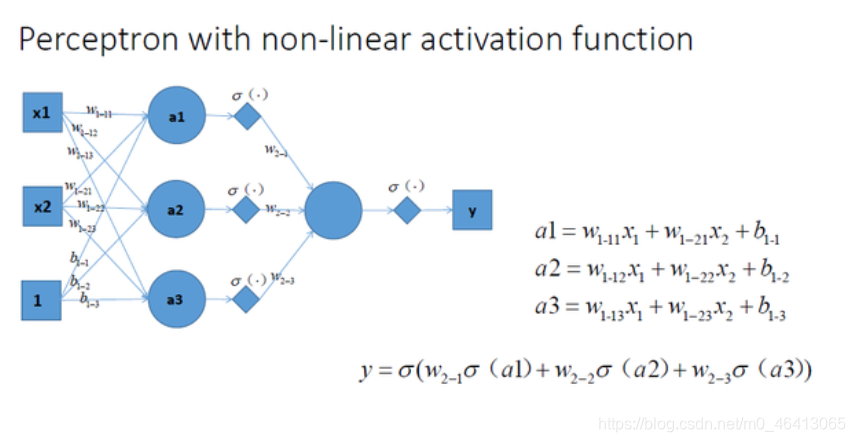
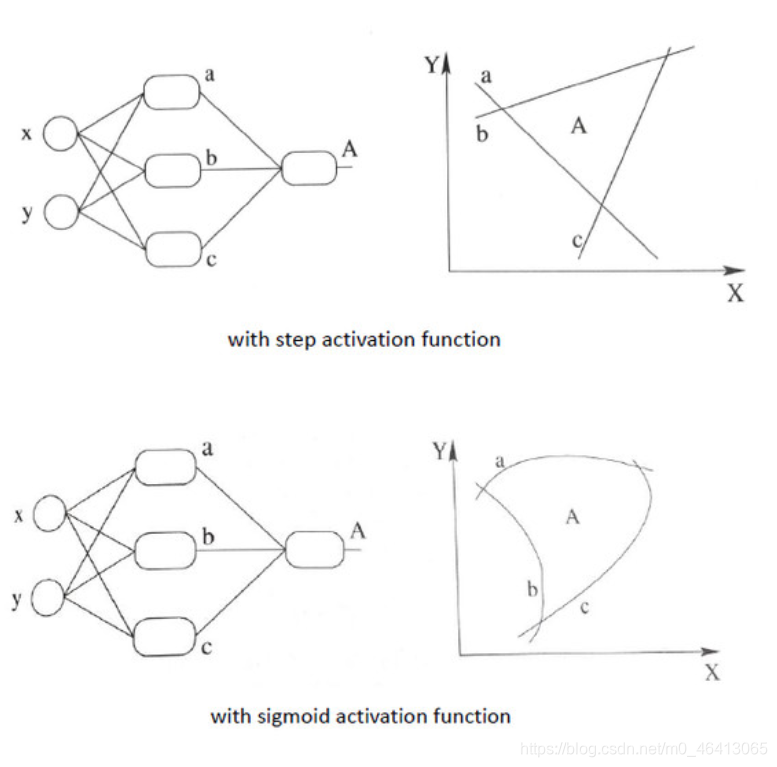
加入非线性激励函数后，神经网络就有可能学习到平滑的曲线来分割平面，而不是用复杂的线性组合逼近平滑曲线来分割平面。 这就是为什么我们要有非线性的激活函数的原因。如下图所示说明加入非线性激活函数后的差异，上图为用线性组合逼近平滑曲线来分割平面，下图为平滑的曲线来分割平面：

友情提示：
这里的激励函数不⻅得⼀定是sigmoid function，还可以是其他function(sigmoid function是从Logistic Regression迁移过来的，现在已经较少在Deep learning⾥使⽤了，具体的常用激活函数，我总结为思维导图如下：

Activation Function Mindmap(干货！！！)

Matrix Operation

network的运作过程，我们通常会⽤Matrix Operation来表⽰，以下图为例，假设第⼀层hidden layers的两个neuron，它们的weight分别是w1=1,w2=2,w1’=-1,w2’=1，那就可以把它们排成⼀个matrix： [ 1 − 2 − 1 1 ] \left[ \begin{matrix} 1 & -2 \\ -1 & 1 \\ \end{matrix} \right] [1−1​−21​]
⽽我们的input⼜是⼀个2*1的vector： [ 1 − 1 ] \left[ \begin{matrix} 1 \\ -1 \\ \end{matrix} \right] [1−1​]将w和x相乘，再加上bias的vector： [ 1 − 1 ] \left[ \begin{matrix} 1 \\ -1 \\ \end{matrix} \right] [1−1​]就可以得到这⼀层的vector z，再经过activation function得到这⼀层的output：
(activation function可以是很多类型的function，这⾥还是⽤Logistic Regression迁移过来的sigmoid function作为运算)

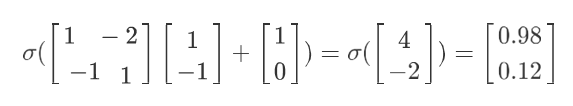
这⾥我们把所有的变量都以matrix的形式表⽰出来
Wⁱ的matrix：

• 每⼀⾏对应的是⼀个neuron的weight
• ⾏数就是feature的个数
  (也是neuron的个数，neuron的本质就是把feature transform到另⼀个space)

input x，bias b和output y都是⼀个列向量

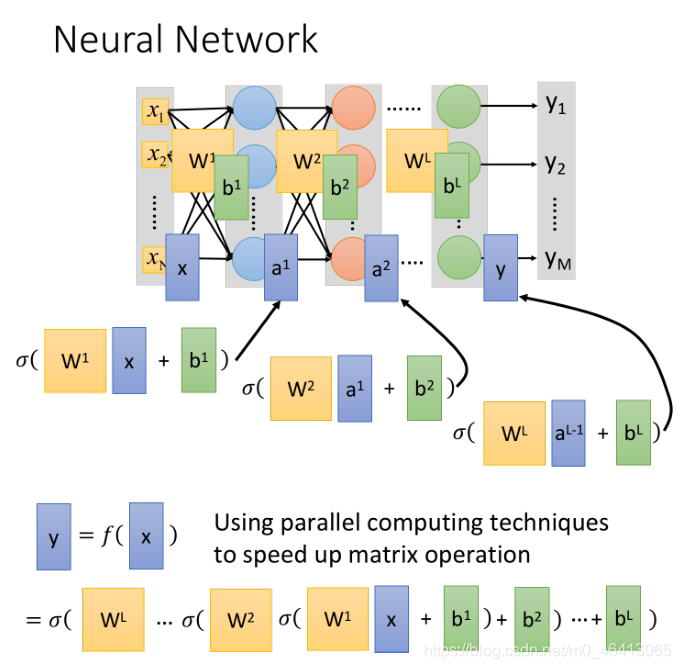
为什么非要表示成矩阵的形式呢？GPU对matrix的运算是⽐CPU要来的快的，所以我们写neural network的时候，习惯把它写成matrix operation，然后call GPU来加速它

Output Layer

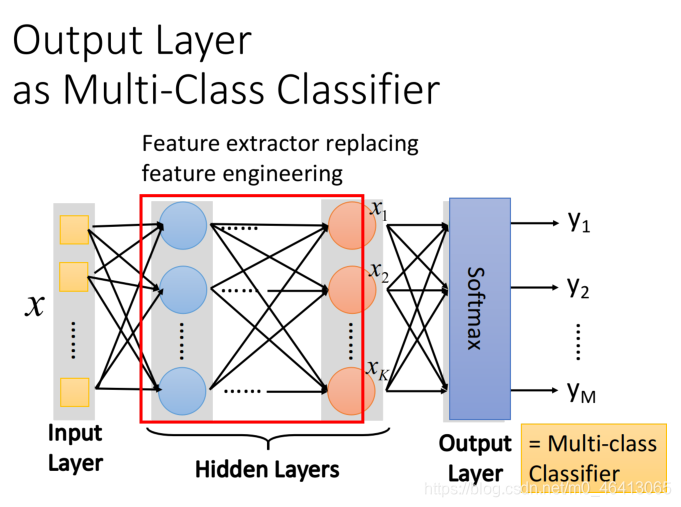
• hidden layers -> feature extractor(特征提取器)
  这个feature extractor就replace了我们之前⼿动做feature engineering，feature transformation这些事情，经过这个feature extractor得到的 就可以被当作⼀组新的feature

• output layer->Multi-class classifier
  拿经过feature extractor转换后的那⼀组⽐较好的feature(能够被很好地separate)进⾏分类的

由于我们把output layer看做是⼀个Multi-class classifier，所以我们会在最后⼀个layer加上softmax

Backpropagation（反向传播）

其实Backpropagation就是DL中的gradient decent算法
因为network parameters θ=w1,w2,…,b1,b2,…⾥⾯可能会有将近million个参数,所以我们引入这种比较有效率的gradient decent算法，使得在计算这个近百万维的gradient的vector的时候更有效率

Chain Rule

Backpropagation⾥⾯的公式推演，唯⼀需要的就只有Chain Rule(链式法则)
在这里，博主又找了一篇博客来给你们回顾一下:

1 复合函数

已知函数y=f(u)，当u表示为u=g(x)时,y作为x的函数就可以表示为y=f(g(x))这样的嵌套结构，这种嵌套结构的函数，就称为f(u)、g(x)的复合函数。

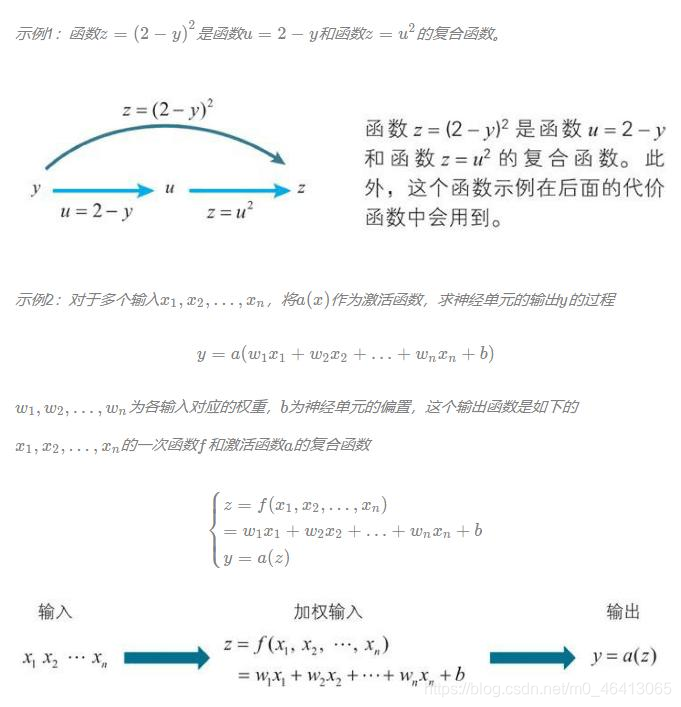
2 链式法则

2.1 单变量函数链式法则

已知单变量函数y=f(u)，当uu表示为单变量函数u=g(x)时，复合函数f(g(x))的导函数可以如下简单地求出来。

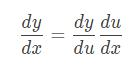
上面这个公式称为单变量函数的复合函数求导公式，也称为链式法则。

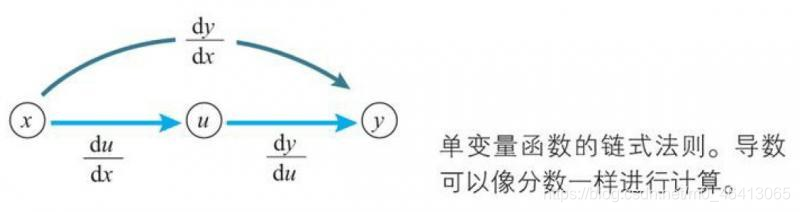
公式的右边，如果将dx、dy、du都看作一个单独的字母，那么公式的左边可以看作将右边进行简单的约分的结果，这个看法总是成立的。通过将导数用dx、dy等表示，我们可以这样记忆链式法则：复合函数的导数可以像分数一样使用约分。但是这个约分的法则不适用于dx、dy的平方等情形。

下面我们来试试对sigmoid与wx+b的复合函数进行求导吧

2.2 多变量函数链式法则

在多变量函数的情况下，链式法则的思想也同样适用。只要像处理分数一样对导数的式子进行变形就行了，但是事情并没有想的那么简单，因为必须要对相关的全部变量应用链式法则。

让我们来看看两个变量的情形。变量z为u、v的函数，如果u、v分别为x、y的函数，则z为x、y的函数，此时下方的多变量函数的链式法则成立。

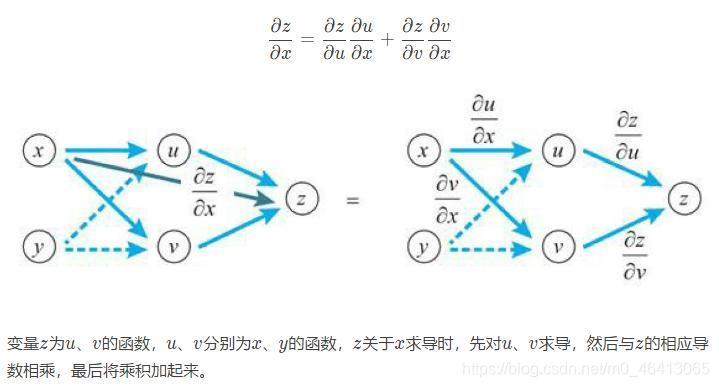
变量z为u、v的函数，u、v分别为x、y的函数，z关于x求导时，先对u、v求导，然后与z的相应导数相乘，最后将乘积加起来。

z关于y求导时，也是如此。下方式子依旧成立。

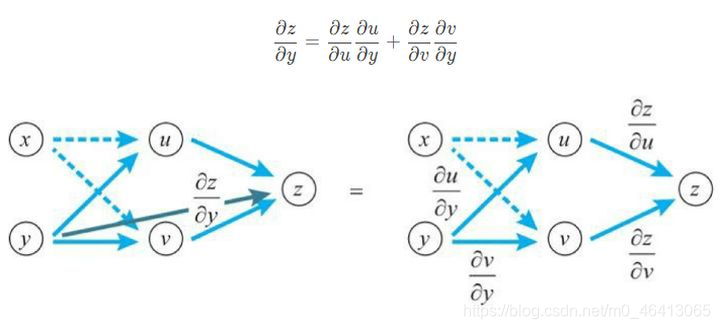
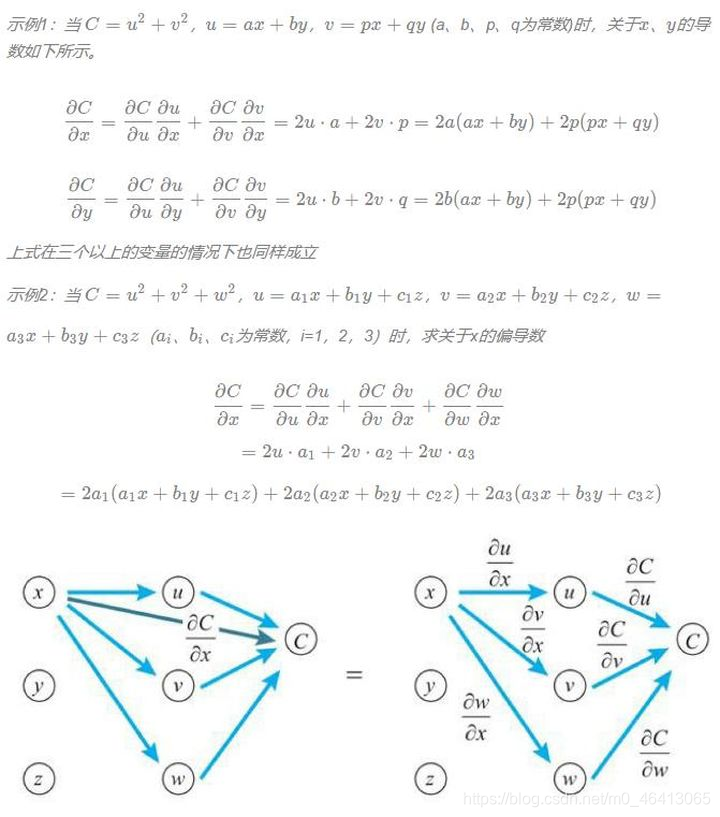
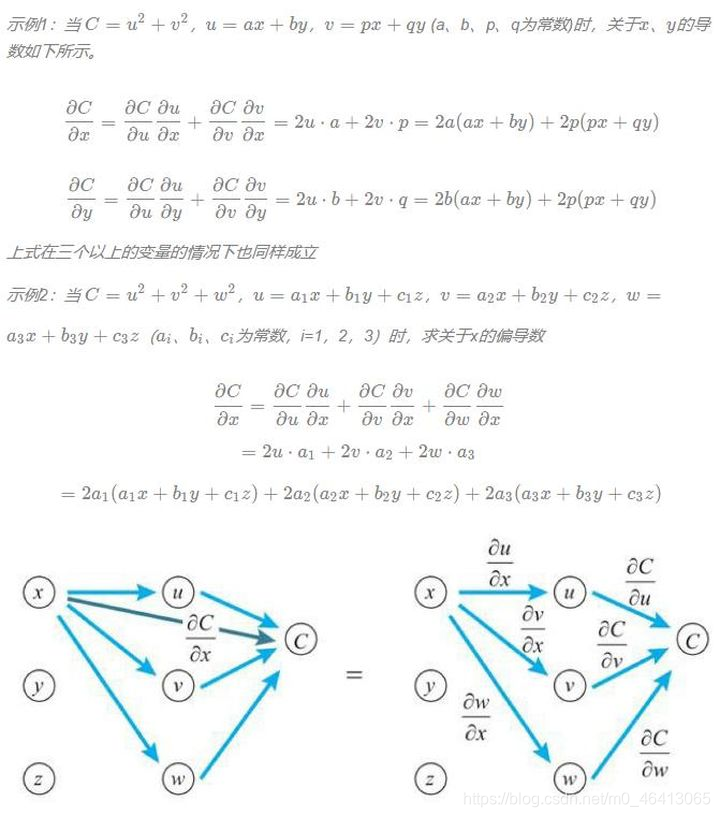
李宏毅老师回顾的Chain Rule试是这样的：

对整个neural network，我们定义了⼀个loss function：

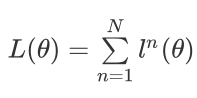
它等于所有training data的loss之和

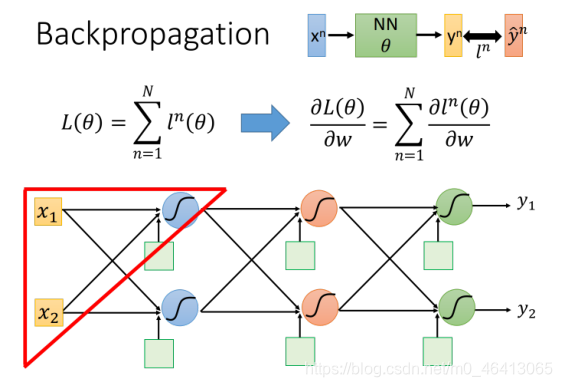
我们把training data⾥任意⼀个样本点xⁿ代到neural network⾥⾯，它会output⼀个yⁿ，我们把这个output跟样本点本⾝的label标注的target y ^ n \hat{y}^n y^​n作cross entropy，这个交叉熵定义了output 和target之间的距离 ，如果cross entropy⽐较⼤的话，说明output和target之间距离很远，这个network的parameter的loss是⽐较⼤的，反之则说明这组parameter是⽐较好的然后summation over所有training data的cross entropy lⁿ(θ)，得到total lossL(θ) ，这就是我们的loss function，⽤这个L(θ)对某⼀个参数w做偏微分，表达式如下：

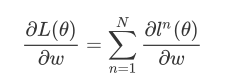
Backpropagation Mindmap（干货！！！）

我把整个流程总结为如下思维导图：

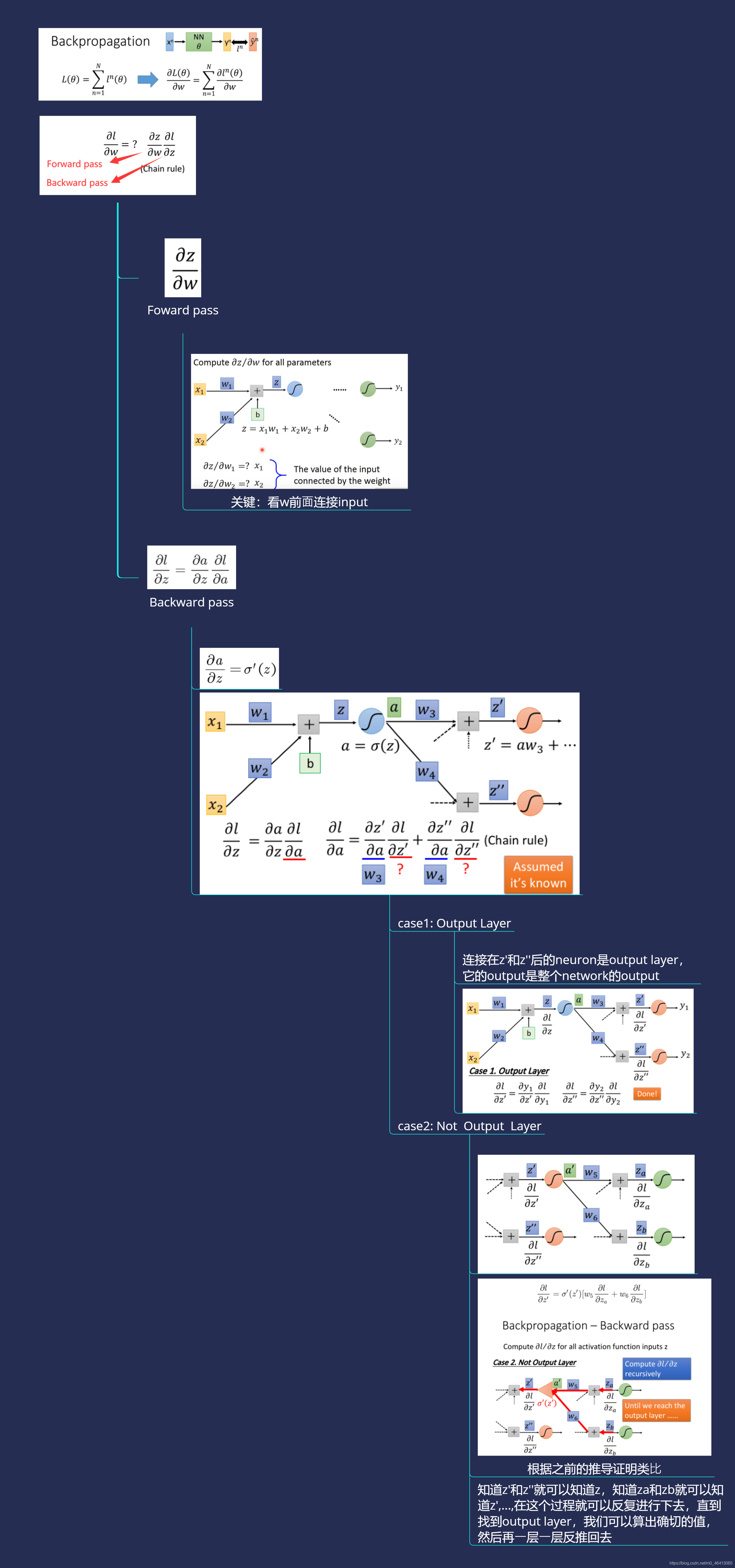
上面说到知道z’和z’‘就可以知道z，知道za和zb就可以知道z’,…,在这个过程就可以反复进行下去，直到找到output layer，我们可以算出确切的值，然后再⼀层⼀层反推回去。

但是转念一想，每次要算⼀个微分的值，都要⼀路往后⾛，⼀直⾛到network的output，如果写成表达式的话，⼀层⼀层往后展开，感觉会是⼀个很可怕的式⼦。
但是！有没有想过换⼀个⽅向计算会怎样呢？

从output layer的 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l​开始算，你就会发现它的运算量跟原来的network的Feedforward path其实是⼀样的。

假设现在有6个neuron，每⼀个neuron的activation function的input分别是z1、z2、z3、z4、z5、z6
，我们要计算l对这些z的偏微分，按照原来的思路，我们想要知道z1的偏微分，就要去算z3和z4的偏微分，想要知道z3和z4的偏微分，就⼜要去计算两遍z5和z6的偏微分，因此如果我们是从z1、z2的偏微分开始算，那就没有效率。
但是，如果反过来先去计算z5和z6的偏微分的话，这个process，就突然之间变得有效率起来了。

Summary
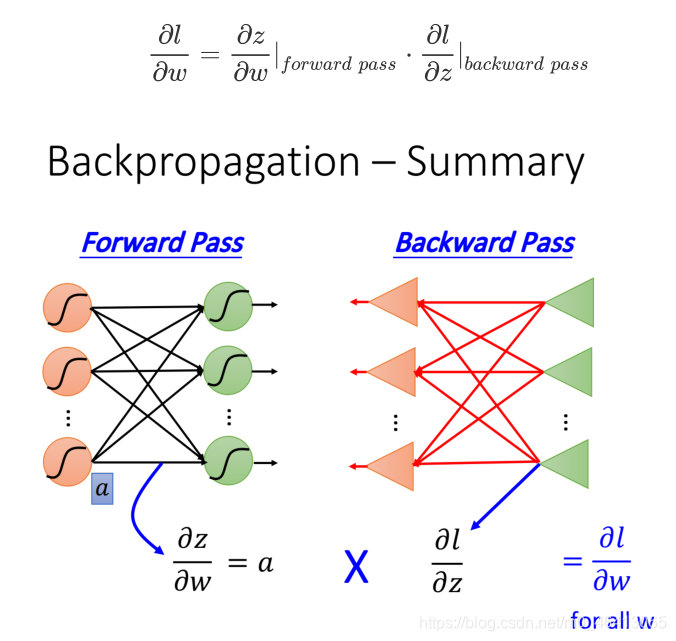
最后，我们来总结⼀下Backpropagation是怎么做的

• Forward pass： 每个neuron的activation function的output，就是它所连接的weight的 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z​

• Backward pass： 建⼀个与原来⽅向相反的neural network，它的三⻆形neuron的output就是 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l​

• 把通过forward pass得到的 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z​和通过backward pass得到的 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l​乘起来就可以得到l对w的偏微分

参考文章

Deep Learning 神经网络基础
神经网络浅讲:从神经元到深度学习
通俗理解神经网络之激励函数(Activation Function)
深度学习数学基础之链式法则