目录
1.小红的子串1.题目链接2.算法原理详解 && 代码实现 2.kotori和抽卡1.题目链接2.算法原理详解 && 代码实现 3.ruby和薯条1题目链接2.算法原理详解 && 代码实现
1.小红的子串
1.题目链接
小红的子串2.算法原理详解 && 代码实现
解法:前缀和思想 + 滑动窗口 求种类个数在[1, count]区间内⼦串的个数:滑动窗⼝两次滑动窗口:利⽤前缀和的思想,求种类个数在[l, r]区间内⼦串的个数,等于求[1, r]区间内个数[1, l - 1]区间内个数 #include <iostream>#include <string>using namespace std;int n = 0, l = 0, r = 0;string str;long long Find(int x){ if(x == 0) { return 0; } int left = 0, right = 0; int hash[26] = { 0 }, kinds = 0; long long ret = 0; while(right < n) { if(hash[str[right] - 'a']++ == 0) { kinds++; } while(kinds > x) { if(hash[str[left] - 'a']-- == 1) { kinds--; } left++; } ret += right - left + 1; // 字符的个数等于新多出来的字串的个数 right++; } return ret;}int main(){ cin >> n >> l >> r >> str; cout << Find(r) - Find(l - 1) << endl; return 0;}2.kotori和抽卡
1.题目链接
kotori和抽卡2.算法原理详解 && 代码实现
解法:代入概率公式 --> C n m ∗ p m ∗ ( 1 − p ) n − m C_n^m * p^m * (1-p)^{n-m} Cnm∗pm∗(1−p)n−m#include <iostream>using namespace std;int main(){ // Cnm int n = 0, m = 0; cin >> n >> m; double ret = 1.0; for(int i = n; i >= n - m + 1; i--) { ret *= i; } for(int i = m; i >= 2; i--) { ret /= i; } for(int i = 0; i < m; i++) { ret *= 0.8; } for(int i = 0; i < n - m; i++) { ret *= 0.2; } printf("%.4lf", ret); return 0;}3.ruby和薯条
1题目链接
ruby和薯条2.算法原理详解 && 代码实现
解法一:排序 + 二分
解法二:排序 + 滑动窗口 + 前缀和
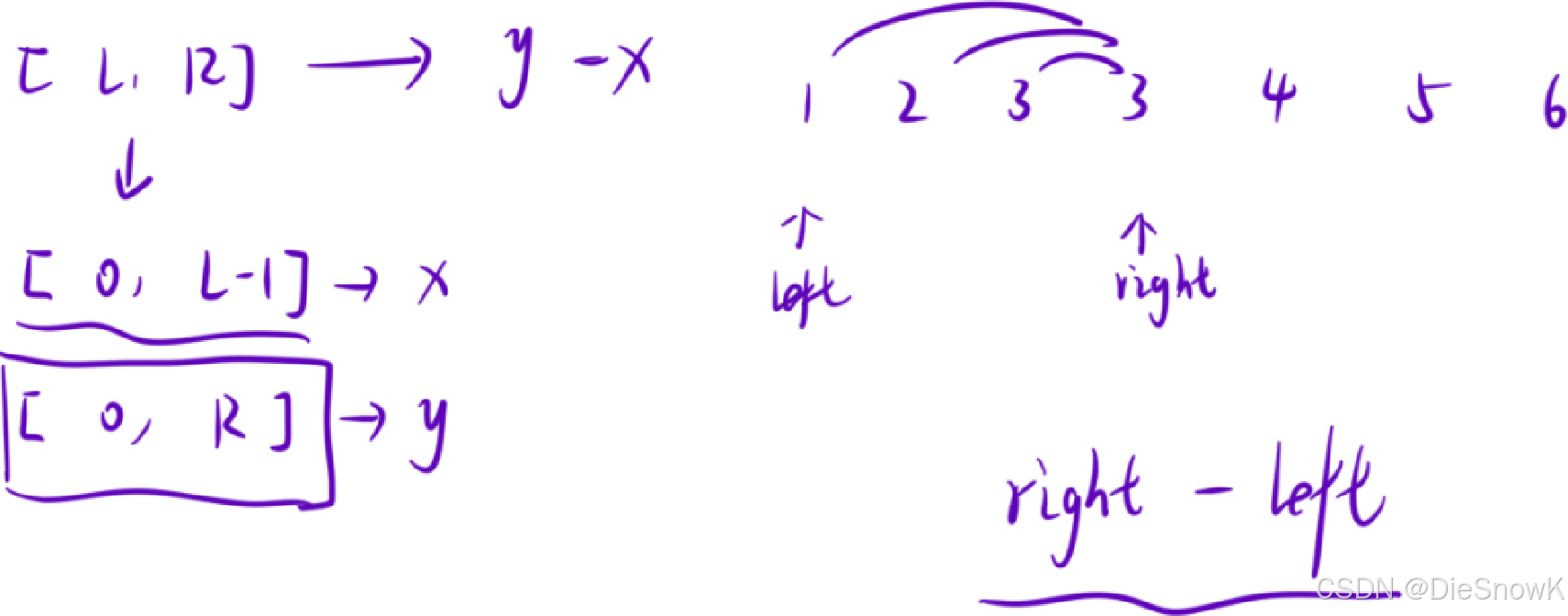
#include <iostream>#include <algorithm>#include <vector>using namespace std;int n = 0, l = 0, r = 0;vector<int> arr;// 找出差值在[0, x]之间一共有多少对long long Find(int x){ int left = 0, right = 0; long long ret = 0; while(right < n) { while(arr[right] - arr[left] > x) { left++; } ret += right - left; right++; } return ret;}int main(){ cin >> n >> l >> r; arr.resize(n, 0); for(auto& x : arr) { cin >> x; } sort(arr.begin(), arr.end()); cout << Find(r) - Find(l - 1) << endl; return 0;}