参考视频:simulink1.1simulink简介_哔哩哔哩_bilibili
一、离散模块库中的模块概览
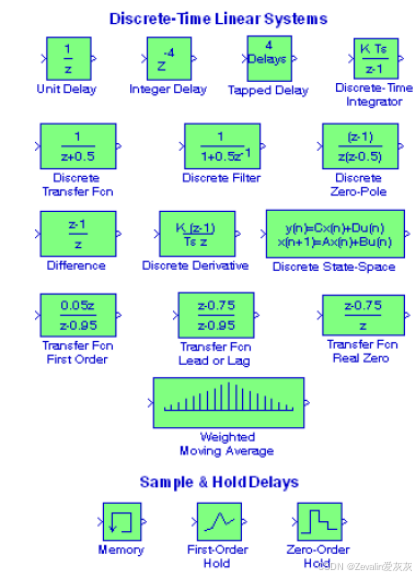
二、几种延迟模块
1、Unit Delay单位延迟模块
(1)在数学领域中,单位延迟模块相当于操作算子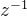 ,该操作算子是构成离散系统的基础。
,该操作算子是构成离散系统的基础。
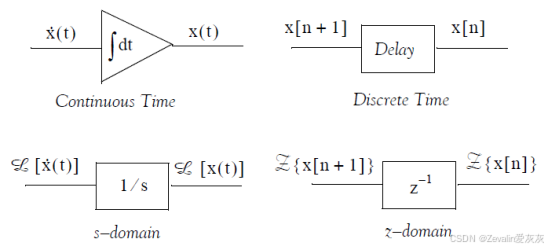
(2)在simulink中,Unit delay单位延迟模块可实现输入信号延迟一个采样周期输出的功能。
(3)下例中的正弦信号发生器需要更改为基于采样的离散形式(默认是基于时间的连续形式),采样时间(Sample time)为0.1秒,信号每个周期的采样次数为50次。
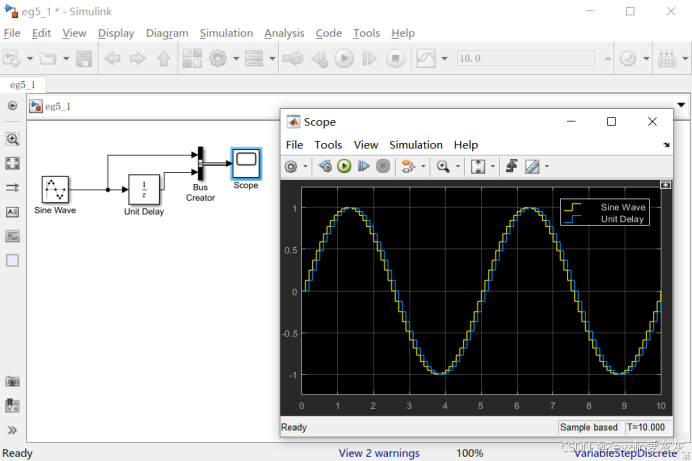
2、Integer Delay积分延迟模块
(1)积分延迟模块算是单位延迟模块的扩展,它可以设置延时参数,以采样周期为单位,延时参数是多少,积分延迟模块就实现输入信号延迟多少个采样周期(可认为积分延迟模块由若干个单位延迟模块串联构成)。
(2)有些版本的simulink只有Variable Integer Delay可变积分延迟模块,实际上这个模块已经集成了积分延迟模块的功能,它在积分延迟模块的基础上让延时参数由外部输入信号决定,如果想直接在模块属性中设定延时参数,将下图所示的“Source”设置为“Dialog”即可。
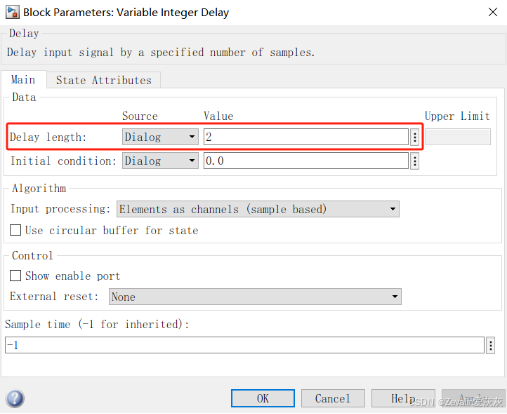
(3)下例中的正弦信号发生器需要更改为基于采样的离散形式(默认是基于时间的连续形式),采样时间(Sample time)为0.1秒,信号每个周期的采样次数为50次。
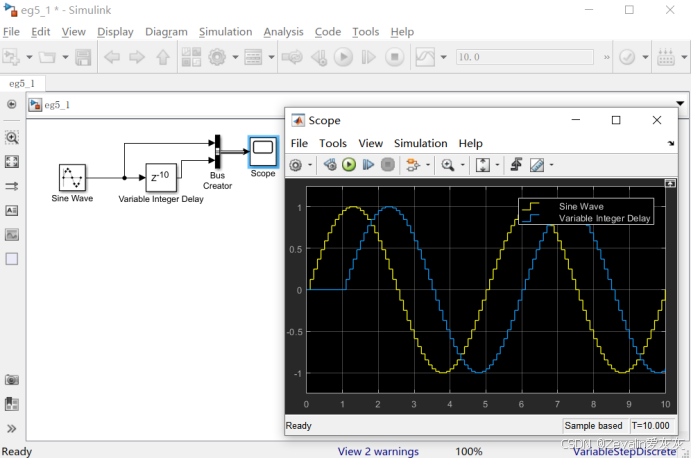
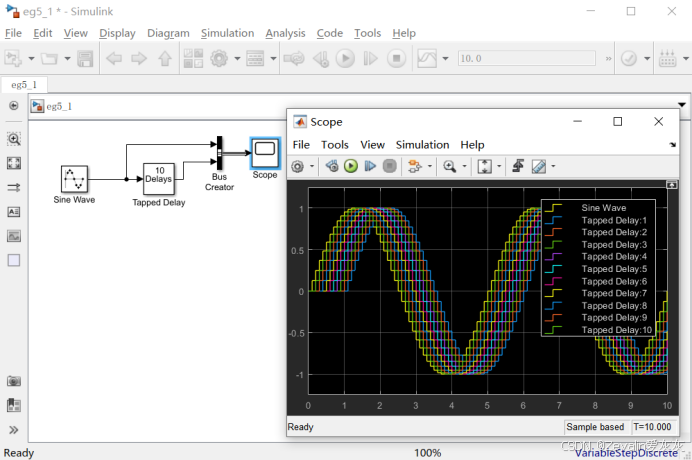
3、Tapped Delay抽头延迟模块
(1)抽头延迟模块可将输入延迟指定数量(延时参数)的采样周期,并为每个延迟版本(不同版本所延迟的采样周期不同)提供一个输出信号(这些输出信号通过同一根信号线输出,所以它们同时还面临排序问题,信号根据延迟的采样周期数量排序,可选择“最老”或者“最新”延迟版本排在前面)。
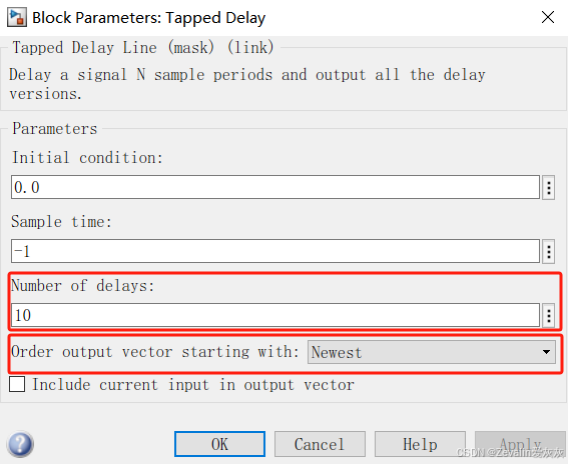
(2)下例中的正弦信号发生器需要更改为基于采样的离散形式(默认是基于时间的连续形式),采样时间(Sample time)为0.1秒,信号每个周期的采样次数为50次。
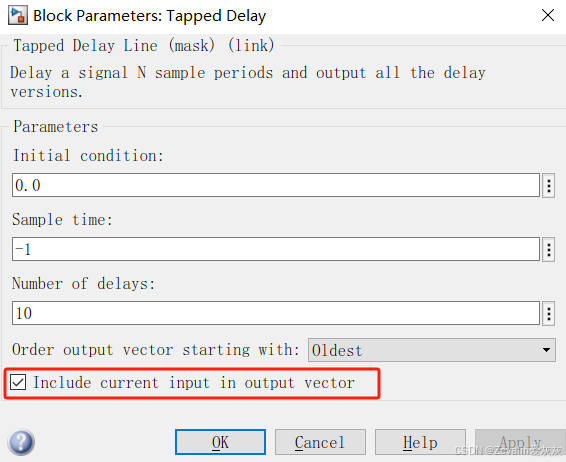
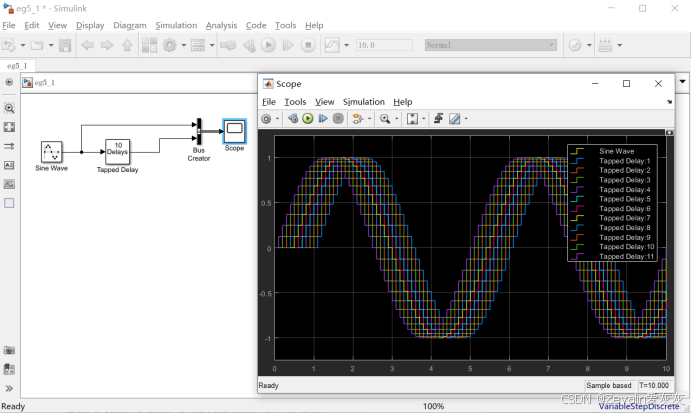
(3)可以选择包含当前输入在输出向量中,也就是在为每个延迟版本提供输出信号的基础上,再为没经过延迟处理的输入信号提供一个输出信号。
三、离散传递函数、零极点、状态空间模块
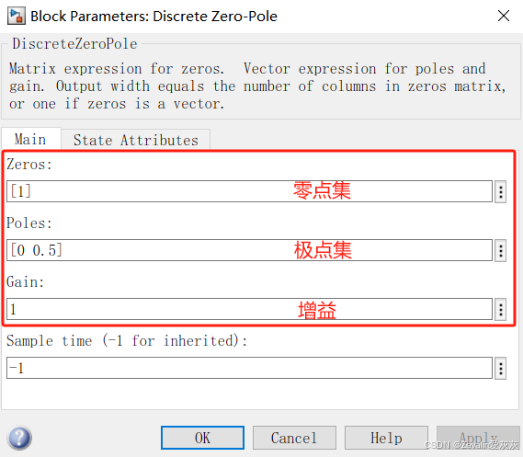
1、Discrete Zero-Pole离散零极点增益模块
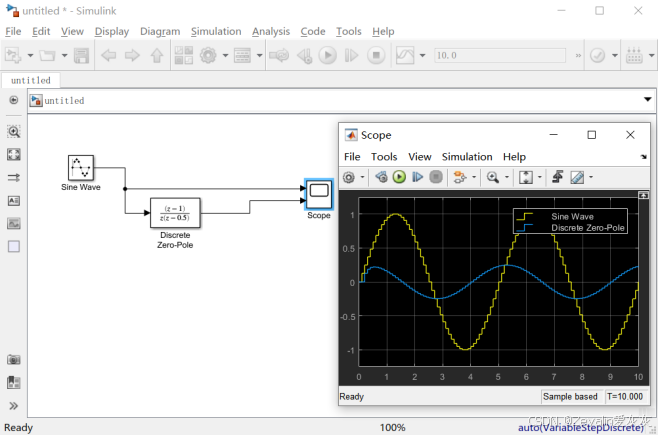
离散零极点增益可用来描述离散传递函数,它可以和离散传递函数互相转换,用零极点增益表示时能很方便地看出其对应离散传递函数的零点、极点和增益。
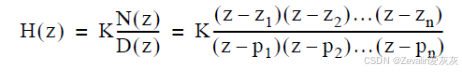
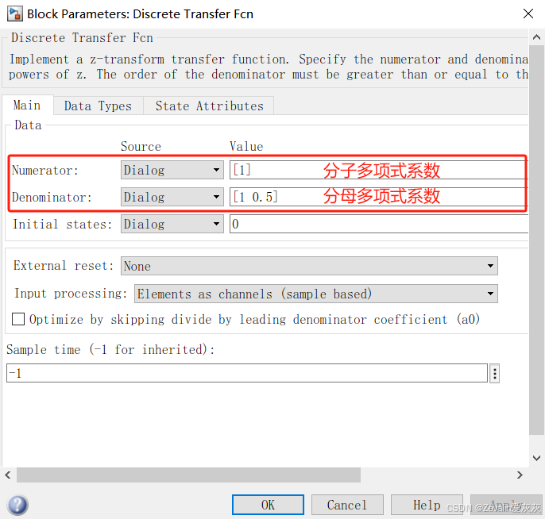
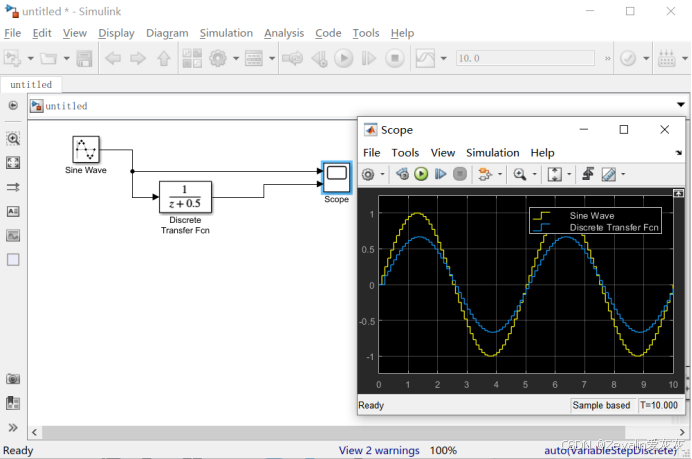
2、Discrete Transfer Fcn离散传递函数模块
离散传递函数模块可以模拟离散传递函数,它只有一个输入端口和一个输出端口,双击模块可以设置传递函数分子和分母的多项式系数(非最高次项若系数为0,切记不要省略)。
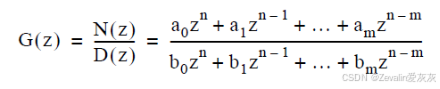
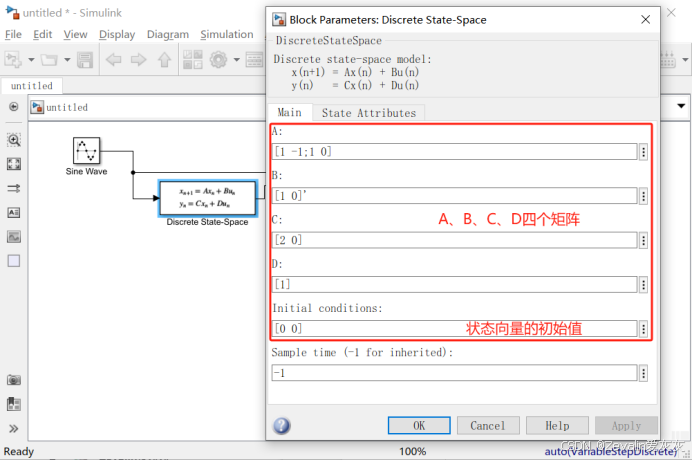
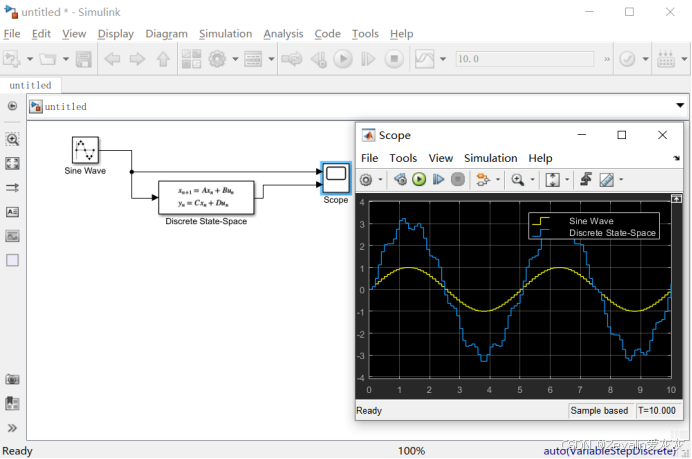
3、Discrete State-Space离散状态空间模块
使用状态空间法求出离散传递函数对应的四个矩阵后,可以直接将输入信号接进离散状态空间模块,该模块将会根据四个矩阵对应的离散传递函数输出求解结果。
4、tf、zpk、ss函数
(1)tf、zpk、ss这三个函数可以实现离散传递函数在一般形式、零极点增益形式和状态空间形式(含四个矩阵的结构体表示)之间互相切换。
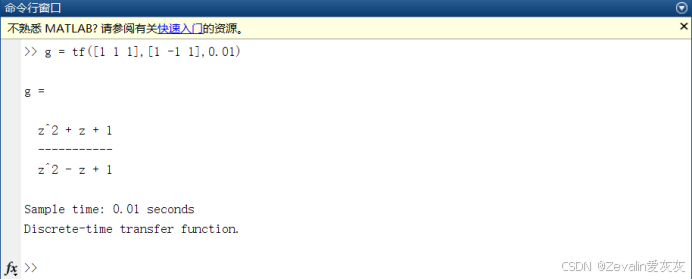
(2)tf函数构造一般形式离散传递函数:只要在第一个参数输入传递函数分子多项式系数矩阵,在第二个参数输入传递函数分母多项式系数矩阵,在第三个参数输入采样时间间隔,即可构造出一般形式离散传递函数。
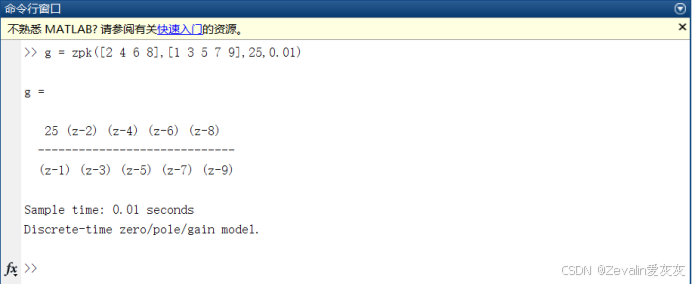
(3)zpk函数构造零极点增益形式离散传递函数:该函数的第一个参数是零点集,第二个参数是极点集,第三个参数是增益,第四个参数是采样时间间隔,zpk函数根据这四个参数构造出零极点增益形式离散传递函数。
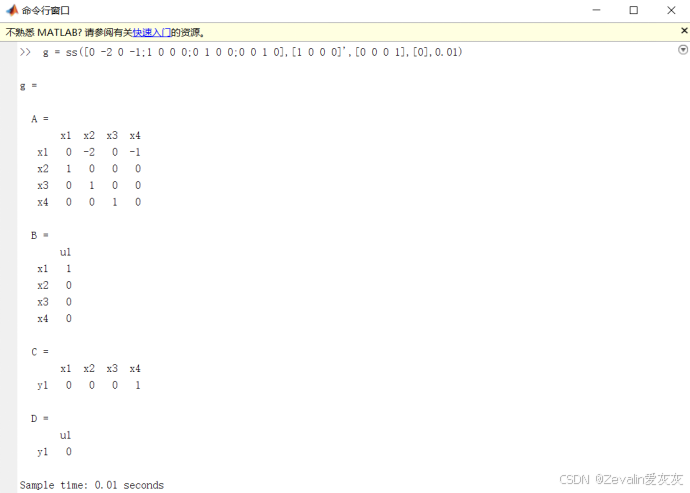
(4)ss函数构状态空间形式离散传递函数:将A、B、C、D四个矩阵依次作为ss函数的参数,最后一个参数是采样时间间隔,ss函数会根据这五个参数构造出离散状态空间形式传递函数,以含四个矩阵的结构体形式返回。
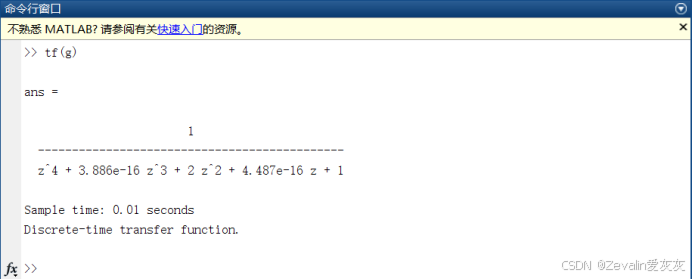
(5)tf函数、zpk函数和ss函数,它们的参数还可以是一般形式、状态空间形式(含四个矩阵的结构体表示)或者零极点增益形式的离散传递函数,执行的功能是将离散传递函数转化为另一种表现形式,比如将含四个矩阵的结构体作为tf函数的参数,tf函数会根据这个结构体构造出一般形式的离散传递函数。(下图中的传递函数g与上图相同)
四、离散滤波器模块
1、Discrete Filter离散IIR(无限脉冲响应)滤波器模块
(1)双击模块,可以在“Main”一栏中设置分子多项式系数和分母多项式系数、以及初始状态和采样时间(采样时间填写“-1”,表示继承输入信号来源模块的采样时间)。
(2)当指定分子多项式系数和分母多项式系数时,需要注意的是多项式各项是按照底数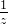 、指数从0开始逐次加1进行排列的,也就是
、指数从0开始逐次加1进行排列的,也就是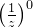 、
、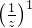 、
、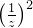 ……
……
(3)举例:使用以下传递函数进行滤波。
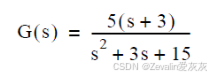
①将连续传递函数转换为离散传递函数(借助billinear函数)。
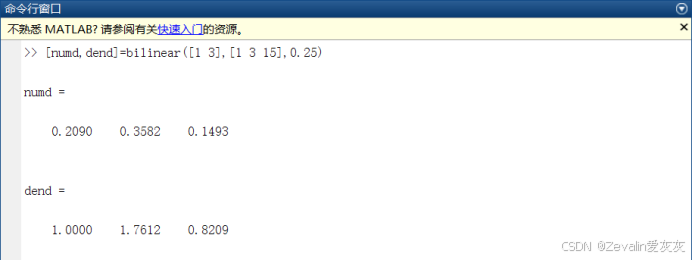
②搭建模型,离散滤波器模块中的传递函数分子多项式系数和分子多项式系数直接填写bilinear返回的两个向量即可。
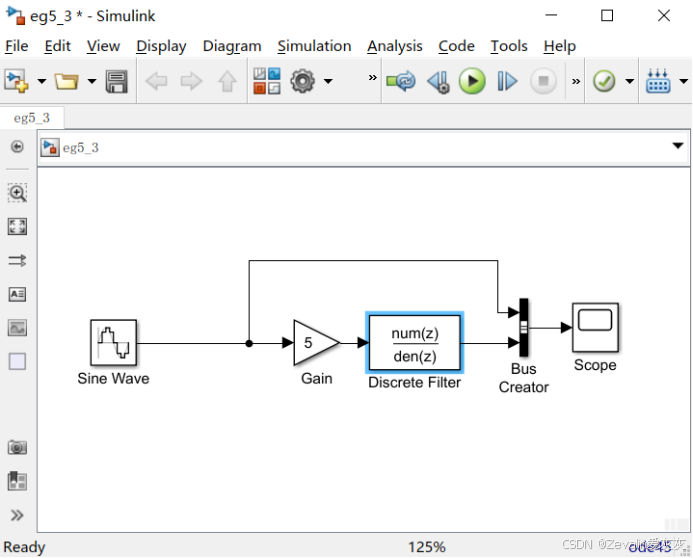
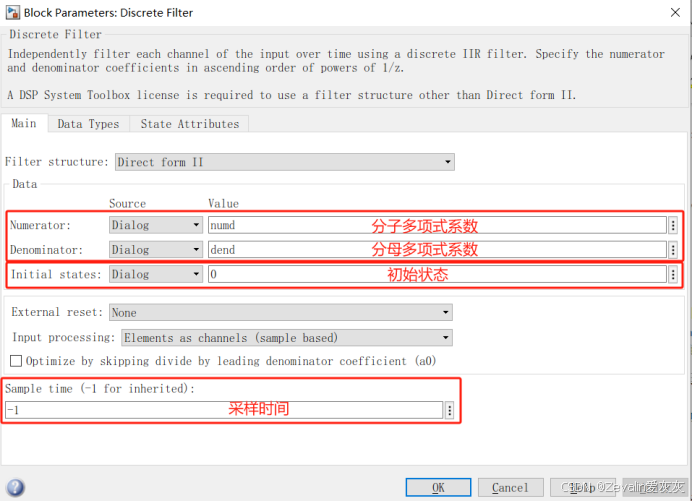
③仿真结果如下图所示。
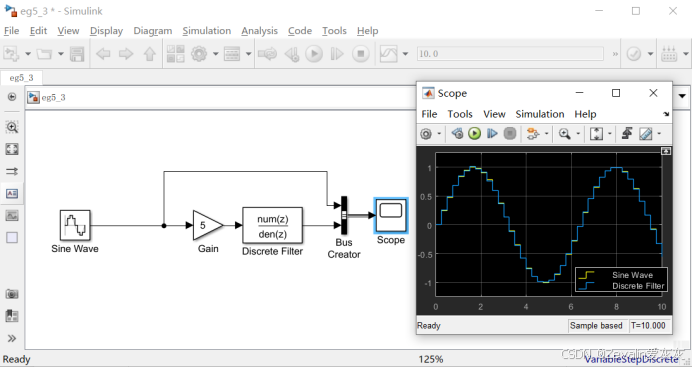
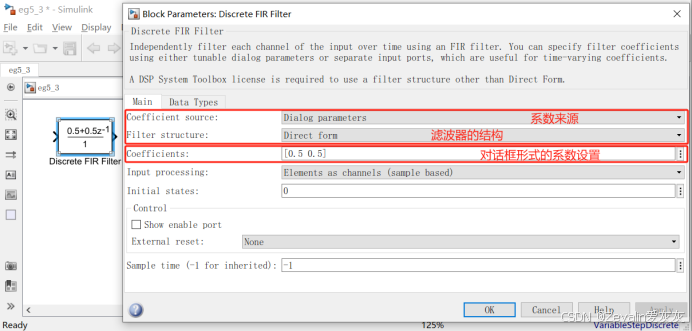
2、Discrete FIR Filter离散FIR滤波器模块
(1)离散FIR滤波器模块可以选择滤波器的结构,默认情况下是直接形式(Direct form),如果想选择其它形式,首先必须安装相应的信号处理工具箱。
(2)系数来源可以以对话框(Dialog parameters,适合时不变系数)的方式进行调整,也可以输入端口(Input port,适合时变系数)的方式进行调整。
五、差分及离散微积分
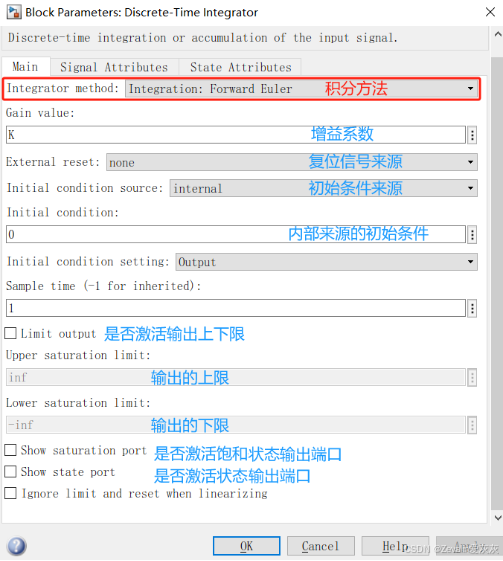
1、Discrete-Time Integrator离散时间积分模块
(1)离散时间积分模块可构建离散时间积分器,其中T为步长,值可以自取,积分方法可采取前向欧拉法、后向欧拉法和梯形法(梯形法的表达式如下所示)三种。
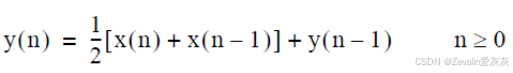
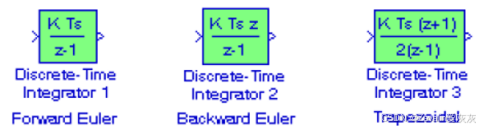
(2)离散时间积分模块可构建离散时间累加器,其中T为步长,值固定为1,累加方法可采取前向欧拉法、后向欧拉法和梯形法三种。


2、Difference差分模块
(1)差分模块的作用是计算当前输入信号值与上一采样时间点输入信号值的差,将其作为输出信号输出。
(2)在仿真开始时,差分模块并不知道上一采样时间点的输入信号值,所以要为其设置初始条件,初始条件作为仿真开始时输入信号“上一采样时间点”的值。
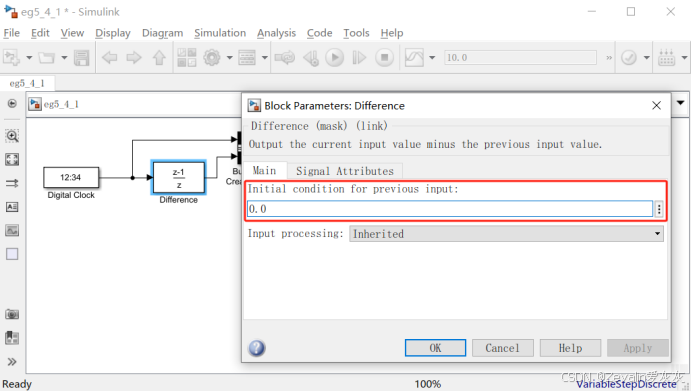
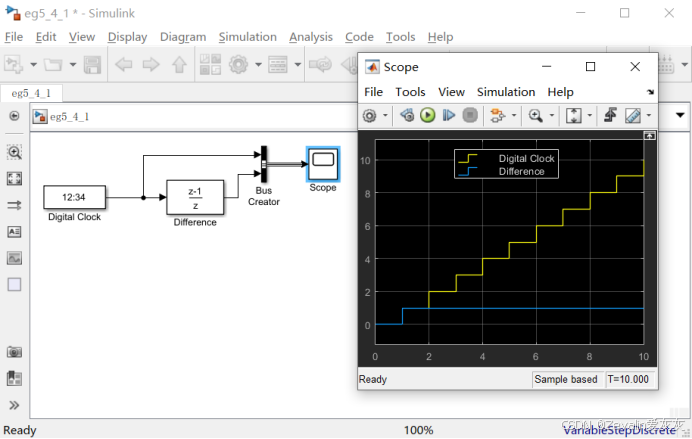
(3)下图运用了Digital Clock数字时钟模块,它能根据当前采样时刻输出当前的仿真时长,本例中令它每隔1秒采集一次当前仿真时长。
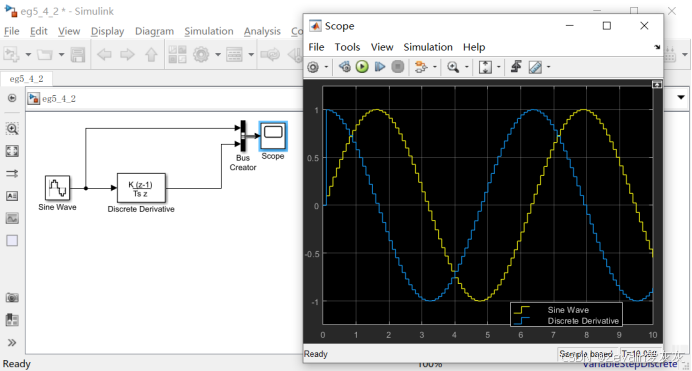
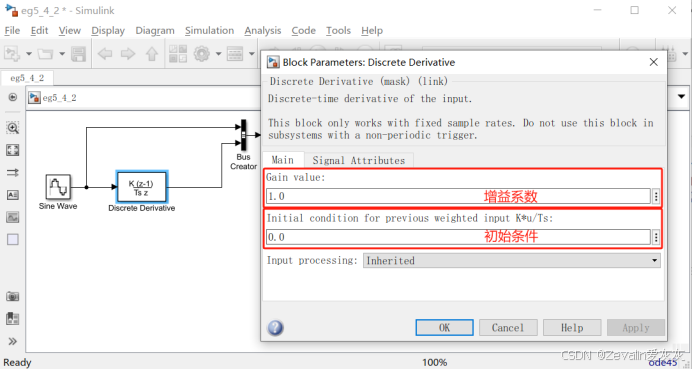
3、Discrete Derivative离散微分模块
(1)离散微分模块的作用是计算当前输入信号值与上一采样时间点输入信号值的差除以采样时间间隔,将计算结果作为输出信号输出。
(2)在仿真开始时,离散微分模块并不知道上一采样时间点的输入信号值,所以要为其设置初始条件,初始条件作为仿真开始时输入信号“上一采样时间点”的值(这里需要输入的是K*u/Ts,也就是“上一采样时间点”的值需要乘上增益系数再除以采样时间间隔)。
(3)下图是对离散正弦波进行离散微分的仿真结果。