在往期文章【技术流派】教你提高双目立体视觉系统的精度!中,博主关于立体视觉系统的精度做了一个较为具体的分析,但整体来说是定性的,本篇再次关于精度做一次定量分析,毕竟绝大部分场景下精度都始终是第一要素,定量分析更有助于系统设计和精度优化。希望看完此篇,读者能更深一步了解精度的决定因素以及它们各自对精度所影响的尺度,以及能够回答如下三个问题:
1. 双目立体视觉系统的精度由那些因素决定?
2. 各个因素对精度的决定程度一样吗?
3. X/Y/Z三个方向的精度都是一样的吗?如果不是一样,哪个方向精度更好呢?
文章目录
- Z方向精度
- XY方向精度
- X/Z精度曲线
- 参考文献
最常见的情况下,双目立体视觉的最终输出是左相机坐标系下的XYZ坐标,本篇便以这三个分量为精度分析对象。
首先,做一些变量的定义:
b b b:基线长度
f f f:焦距
x , y x,y x,y :像点坐标(以像主点为原点)
X , Y , Z X,Y,Z X,Y,Z:相机坐标系下的坐标
d d d:视差
我们先看这三个分量的求解公式:
Z
=
b
f
d
,
X
=
Z
f
x
,
Y
=
Z
f
y
Z=\frac {bf} d,X=\frac Z f x,Y=\frac Z f y
Z=dbf,X=fZx,Y=fZy
从公式可知,在硬件参数 B , f B,f B,f固定的情况下, X Y Z XYZ XYZ的值和像点坐标值直接相关, X Y Z XYZ XYZ的精度实际上是像点精度下的空间偏差值,因此我们以像点精度为基本(最小)精度单位。
假设像点 x , y x,y x,y的精度为 s x , s y s_x,s_y sx,sy,视差 d d d的精度为 s d s_d sd。通常认为 x , y x,y x,y的精度是相同的,即 s x = s y = s s_x=s_y=s sx=sy=s,而视差的精度一般来说可以用公式 s d = s x 2 s_d = \frac {s_x} {\sqrt 2} sd=2 sx来估计1。
Z方向精度
首先对于
Z
=
b
f
d
Z=\frac {bf} d
Z=dbf,自变量是
d
d
d,我们对
d
d
d求偏导,可得
∂
Z
∂
d
=
−
b
f
d
2
=
−
Z
2
b
f
\frac {\partial Z} {\partial d}=-\frac {bf} {d^2}=-\frac {Z^2} {bf}
∂d∂Z=−d2bf=−bfZ2
因此,
Z
Z
Z方向的精度可以表示为
s
Z
=
Z
2
b
f
s
d
=
Z
2
2
b
f
s
s_Z=\frac {Z^2} {bf}s_d=\frac {Z^2} {\sqrt 2bf}s
sZ=bfZ2sd=2
bfZ2s
可知 Z Z Z方向精度和 Z Z Z的平方正相关,即和物体离相机的距离的平方正相关(严格来说是 Z Z Z方向距离)。
同时,上式可以变换一种形式:
s
Z
=
Z
b
Z
f
s
d
s_Z=\frac {Z} {b}\frac {Z} {f}s_d
sZ=bZfZsd
假设 q = Z b , m = Z f q=\frac {Z} {b},m=\frac {Z} {f} q=bZ,m=fZ,则 q q q是我们所熟知的基高比的倒数, m m m是影像的尺度(即GSD,一个像素代表的空间尺寸),这个公式显示,基高比和GSD对 Z Z Z方向精度起着关键作用,更大的基高比和更小的GSD有助于提高 Z Z Z方向精度。这可以用于指导双目立体视觉系统的设计。
XY方向精度
同理,对于
X
X
X,自变量是
Z
Z
Z和
x
x
x,我们对
Z
Z
Z和
x
x
x求偏导,可得
∂
X
∂
Z
=
x
f
,
∂
X
∂
x
=
=
Z
f
\frac {\partial X} {\partial Z}=\frac x f,\frac {\partial X} {\partial x}==\frac Z f
∂Z∂X=fx,∂x∂X==fZ
X
X
X方向精度可表示为
s
X
=
(
x
f
s
Z
)
2
+
(
Z
f
s
x
)
2
s_X=\sqrt {{(\frac x f s_Z)}^2+{(\frac Z f s_x)}^2}
sX=(fxsZ)2+(fZsx)2
同理,
Y
Y
Y方向精度可表示为
s
Y
=
(
y
f
s
Z
)
2
+
(
Z
f
s
y
)
2
s_Y=\sqrt {{(\frac y f s_Z)}^2+{(\frac Z f s_y)}^2}
sY=(fysZ)2+(fZsy)2
把 s Z = Z 2 2 b f s , s x = s y = s s_Z=\frac {Z^2} {\sqrt 2bf}s,s_x=s_y=s sZ=2 bfZ2s,sx=sy=s代入公式,可得
s
X
=
1
+
(
x
Z
2
f
b
)
2
Z
f
s
=
1
+
(
X
2
b
)
2
Z
f
s
s_X=\sqrt {1+{(\frac {xZ} {\sqrt 2 fb})}^2}\frac Z f s=\sqrt {1+{(\frac X {\sqrt 2 b})}^2}\frac Z f s
sX=1+(2
fbxZ)2
fZs=1+(2
bX)2
fZs
s
Y
=
1
+
(
y
Z
2
f
b
)
2
Z
f
s
=
1
+
(
Y
2
b
)
2
Z
f
s
s_Y=\sqrt {1+{(\frac {yZ} {\sqrt 2 fb})}^2}\frac Z f s=\sqrt {1+{(\frac Y {\sqrt 2 b})}^2}\frac Z f s
sY=1+(2
fbyZ)2
fZs=1+(2
bY)2
fZs
可以看出,
s
X
s_X
sX和
s
Y
s_Y
sY是等尺度的,结合前式,
s
Z
=
Z
2
2
b
f
s
s_Z=\frac {Z^2} {\sqrt 2bf}s
sZ=2
bfZ2s
得到三个方向的精度表达式。
X/Z精度曲线
为了更清晰的观察三个方向精度随着 Z Z Z值变化的趋势,我们来做一个仿真,假设像点精度为10 μ m \mu m μm,计算并绘制 Z Z Z和 X X X方向( Y Y Y方向和 X X X方向等尺度,趋势一致)的精度曲线。
其他参数仿真数据:
f = 1100 f = 1100 f=1100 pix
x = 640 x = 640 x=640 pix
b = 200 b = 200 b=200 mm
绘制的精度曲线如下:
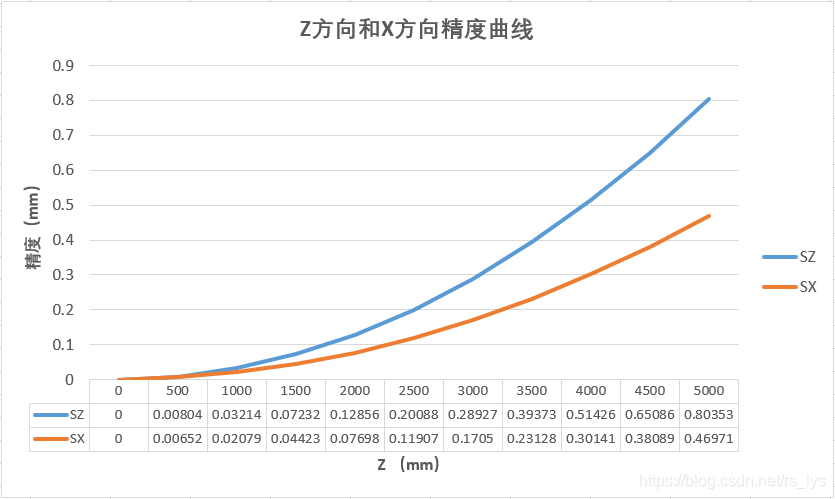
从精度计算的结果和趋势图可以看出,精度数值随着 Z Z Z的增加而变大(意味着精度越来越差),且当 Z Z Z值较大时, Z Z Z方向精度比 X ( Y ) X(Y) X(Y)方向精度要差,随着Z的增加,差距更加明显。
而当
Z
Z
Z值较小时,
Z
Z
Z方向精度反而会比
X
Y
XY
XY方向要好,我们将Z的范围减小到0~500,再绘制一条曲线图,
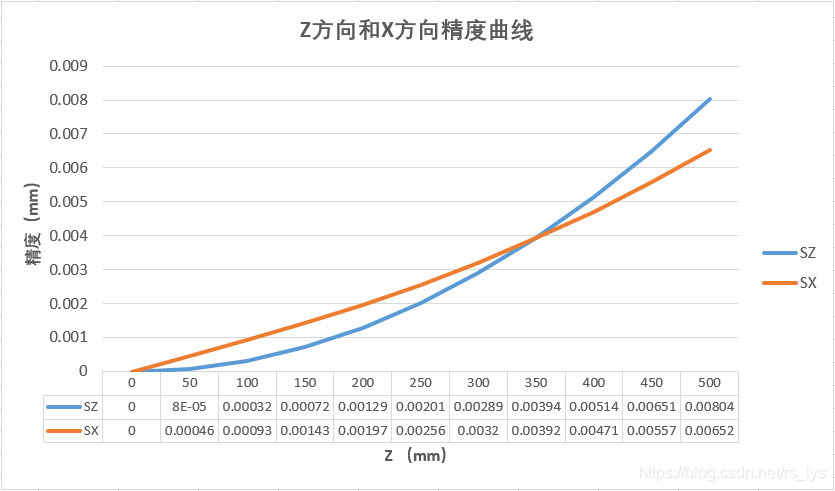
可以看到,在
Z
Z
Z小于350mm左右时,
Z
Z
Z方向精度要好于
X
X
X方向,这个临界
Z
Z
Z值是根据硬件参数和精度公式计算出的,且和像点坐标相关。
参考文献
- [1] Walker, Stewart. Close-Range Photogrammetry and 3D Imaging, 2nd Edition[J]. Photogrammetric Engineering & Remote Sensing, 2015.博主简介:
Ethan Li 李迎松(知乎:李迎松)
武汉大学 摄影测量与遥感专业博士
主方向立体匹配、三维重建
2019年获测绘科技进步一等奖(省部级)
爱三维,爱分享,爱开源
GitHub: https://github.com/ethan-li-coding
个人微信:
欢迎交流!
关注博主,更多三维重建知识科普,感谢!
博客主页:https://ethanli.blog.csdn.net
