1.盛水最多的容器
题目链接:11. 盛最多水的容器 - 力扣(LeetCode)
题目解析:
在解析题目时,我们可以把最直接的方法先列举出来,然后再根据相应的算法原理,来进行优化
思路一:暴力求解
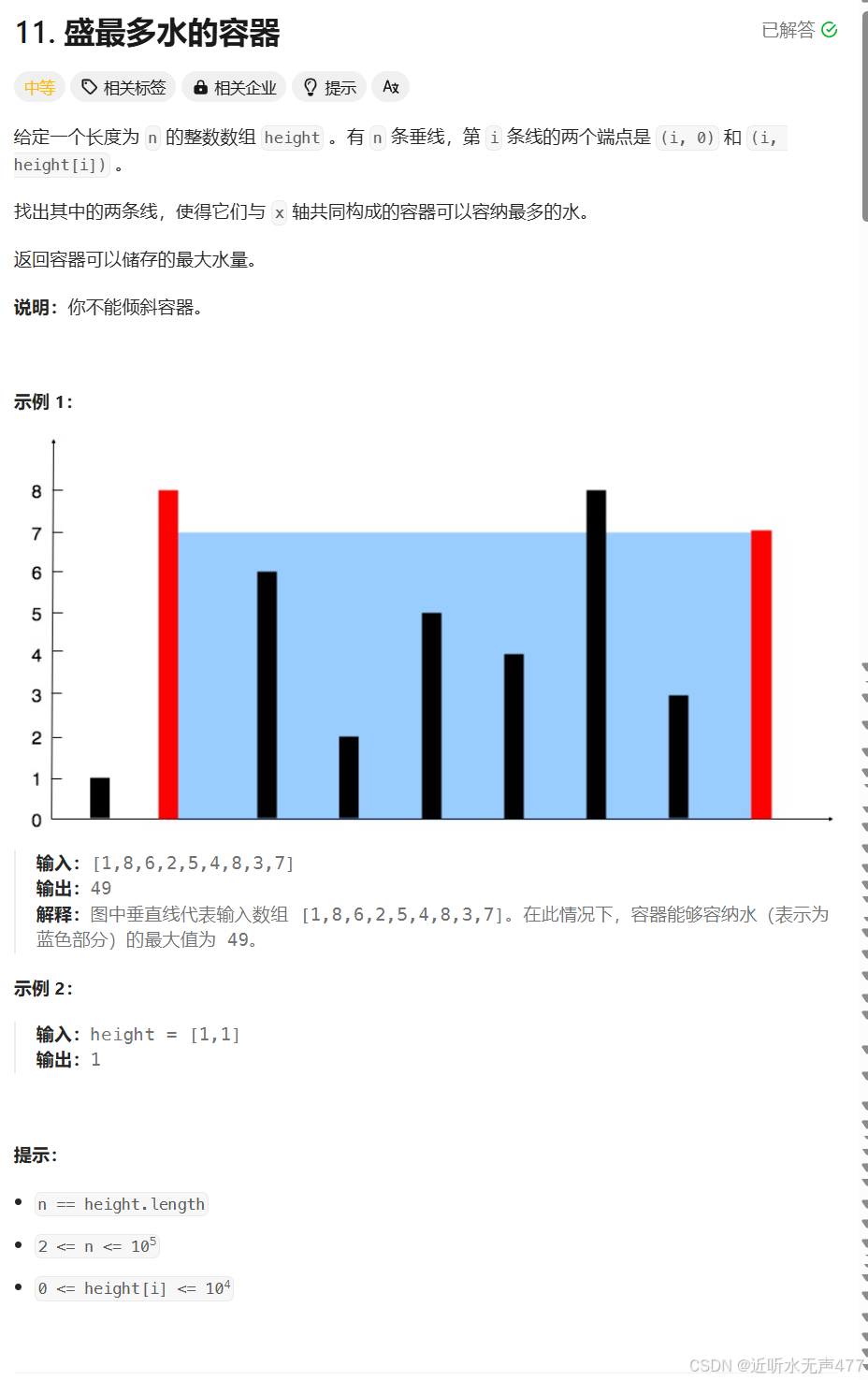
容器的容积计算方法:
假设两个指针i, j分别指向水槽班的两端,此时容器的宽度为j - i。由于容器的高度是有两个板子中的最短板来决定的,因此容积的公式为:
v = (j - i) * min(heght[i], height[j])
算法代码:
class Solution {public: int maxArea(vector<int>& height) { int ret = 0; for (int i = 0; i < height.size() ; i++) { for (int j = i + 1; j < height.size() ; j++) { ret = max(ret, (j - i) * min(height[i], height[j])); } } return ret; }};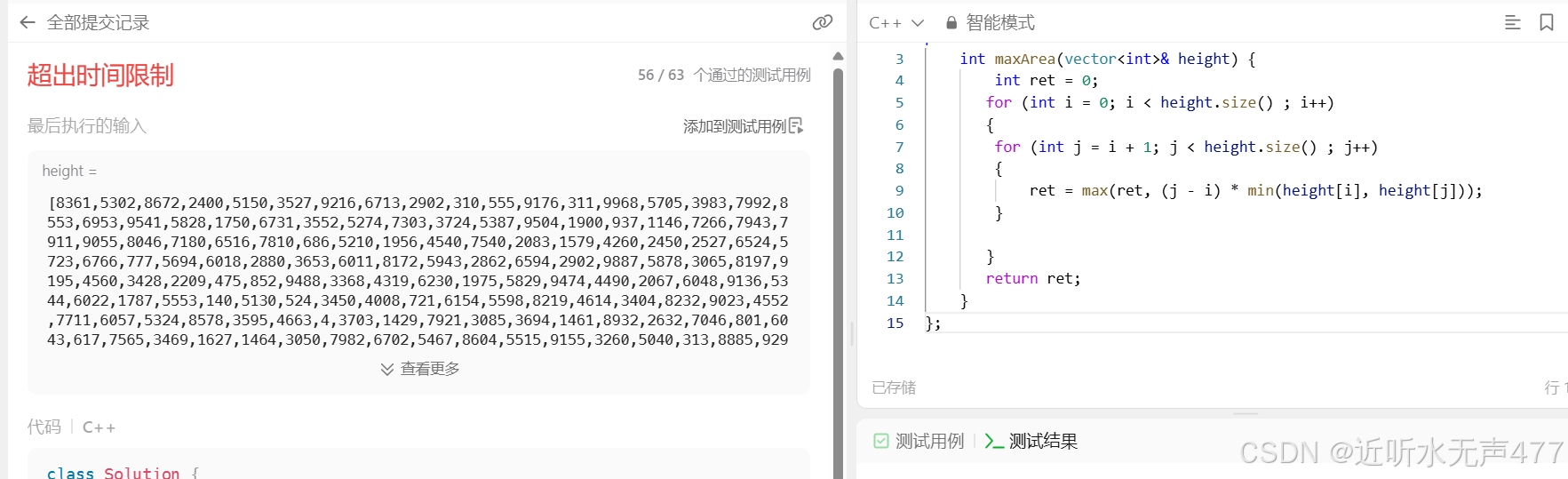
这种解法可以解决部分用例但是是超时的,我们可不可以在暴力算法的基础上进行优化呢?
解法二:对撞指针
假设现在我们有两个指针left, right分别指向容器的左右两个端点,此时容器的容积:
v = (right - left) * min(heigth[left], height[right])
容器的左边界为 height[left] ,右边界height[right]
如果此时,我们来固定一个边界,改变另一个边界,水的容积就会有以下的变换形式:
容器的宽度一定在变小。由于左边界较小,左边界就决定了水柱的高度。如果改变左边界,水柱的高度不会超过右边界,容积可能变高。如果在这种情况下去移动右边界,宽度在减小,水柱的高度也不可能高过有边界,容积就一直在减小。所以,左边界和其余边界的情况都可以直接舍去,这样就可以直接省去大量的枚举过程。
有了上面的理论基础,我们现在开始实现代码:
class Solution {public: int maxArea(vector<int>& height) { int right = height.size() - 1, letf = 0, ret = 0; while (letf < right) { ret = max(ret, (right - letf) * min(height[letf], height[right])); if (height[right] < height[letf]) right--; else letf++; } return ret; }}; 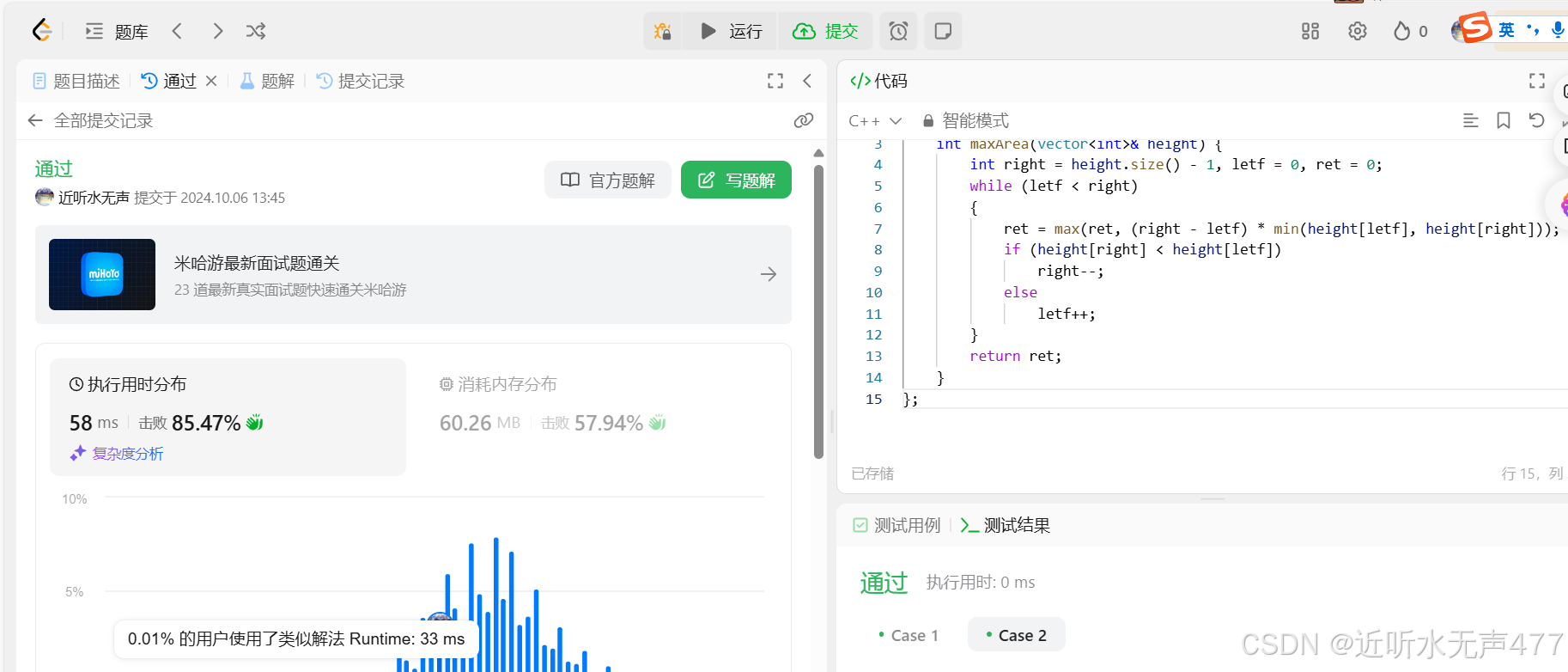
2.有效三角形的个数
题目链接: 611. 有效三角形的个数 - 力扣(LeetCode)

算法思路:
一.暴力枚举(超时)
三层for循环枚举出所有的三元数组,并判断满不满足三角形的成立条件。
这个十分的简单,我们这里就只展现一下代码:
class Solution {public: int triangleNumber(vector<int>& nums) { int ret = 0; //1.现将整个数组进行排序 sort(nums.begin(), nums.end()); //固定最大值 for (int right = nums.size() - 1; right >= 0; right--) { //固定第二大的值 for (int left = right - 1; left >= 0; left--) { for (int i = left - 1; i >= 0; i--) { if (nums[i] + nums[left] > nums[right]) ret++; } } } return ret; }};接下来,我们来优化算法:
解法二:(排序 + 双指针)
1.现将数组进行排序
根据解法一中的优化思想,我们可以固定一个最长的边,然后在比这个边小的数组中找一个二元数组的和大于最大边的,由于数组有序,我们就可以在使用对撞指针来优化。
有了上面的理论基础,我们现在就来实现代码:
class Solution {public: int triangleNumber(vector<int>& nums) { int ret = 0; sort(nums.begin(), nums.end()); //固定最大值 for (int i = nums.size() - 1; i >= 0; i--) { int left = 0, right = i - 1; while (left < right) { //nums此时是一个有序的数组,当遇到nums[left] + nums[right] > nums[i]时, //中间就会有right - left个元素符合条件 if (nums[left] + nums[right] > nums[i]) { ret += right - left; right--; } else left++; } } return ret; }};