连续小波变换是一种数学工具,用于将信号分解为构成其的小波或波形。这种变换在信号处理、图像分析、音频压缩等领域有广泛的应用。与傅里叶变换相比,连续小波变换能提供关于信号在不同时间和尺度上的详细信息,使之更适合分析非平稳信号(即信号的统计特性随时间变化的信号)。
所使用的数据来自于公开的心电信号数据库,获取网址如下:PTB Diagnostic ECG Database v1.0.0 (physionet.org)
本文使用经过预处理的心电信号(ECGs)作为分析例子,所有图片均有它所得到:在我的资源中的"processed_ecg segment_csdn "
连续小波变换的定义
连续小波变换利用一组基函数(称为小波)对信号进行分析。这些小波是由一个母小波通过平移和缩放生成的。母小波 ψ(t) 是一个平均值为零的波形,通常具有快速衰减的特性。通过调整缩放因子 a 和平移参数 b 来生成不同的小波,从而能够聚焦于信号的不同特性。小波变换可以定义为:
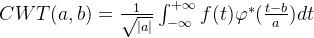
其中f(t) 是输入信号;ψ(t) 是母小波;a 是缩放参数(不等于零),控制小波的伸缩;b 是平移参数,控制小波在时间轴上的位置。
常用的母小波
Haar小波:可能是最简单的小波,适合处理具有突变点的信号;公式为:
![\varphi (t) = \left\{\begin{matrix} 1 &t\in [0, \frac{1}{2}] \\ -1 &t\in[\frac{1}{2}, 1] \\ 0&other \end{matrix}\right.](http://m.zhangshiyu.com/zb_users/upload/2024/10/20241012112108172870326814431.png)
Ricker小波:常用于边缘检测和图像处理中;公式为:
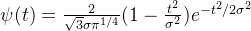
这里的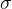 控制波形的宽度,通常取标准差的值。
控制波形的宽度,通常取标准差的值。
Daubechies小波:一系列具有更平滑特性的小波,能更好地捕捉信号的详细信息,一般使用的是db4小波;公式为:
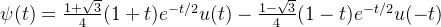
u(t)是信号与系统中的脉冲函数。
Morlet小波:结合了余弦波和高斯函数,适用于频率分析;表达式为:
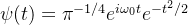
其中,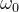 是中心频率。
是中心频率。
连续小波变换的实现
在本文使用Morlet小波作为母小波。首先我们来绘制原始V2导联信号图,绘制代码及图像如下:
import matplotlib.pyplot as pltimport jsonimport matplotlib#字体样式和大小matplotlib.rcParams['font.family'] = 'Times New Roman'matplotlib.rcParams['font.size'] = 26#加载ECG数据,请更换为自己的本地地址with open(r"F:\ecg segment_cwt_csdn.json", "r") as file: ecg_data = json.load(file)signal_data = ecg_data['data']fs = ecg_data['fs'] #加载采样频率 hz=1000# 获取V1导联的数据signal = signal_data['V2']# 创建图表并绘制V1导联plt.figure(figsize=(15, 5))plt.plot(signal)plt.title('V2 Lead ECG Signal')plt.xlabel('Time (samples)')plt.ylabel('Amplitude')plt.show()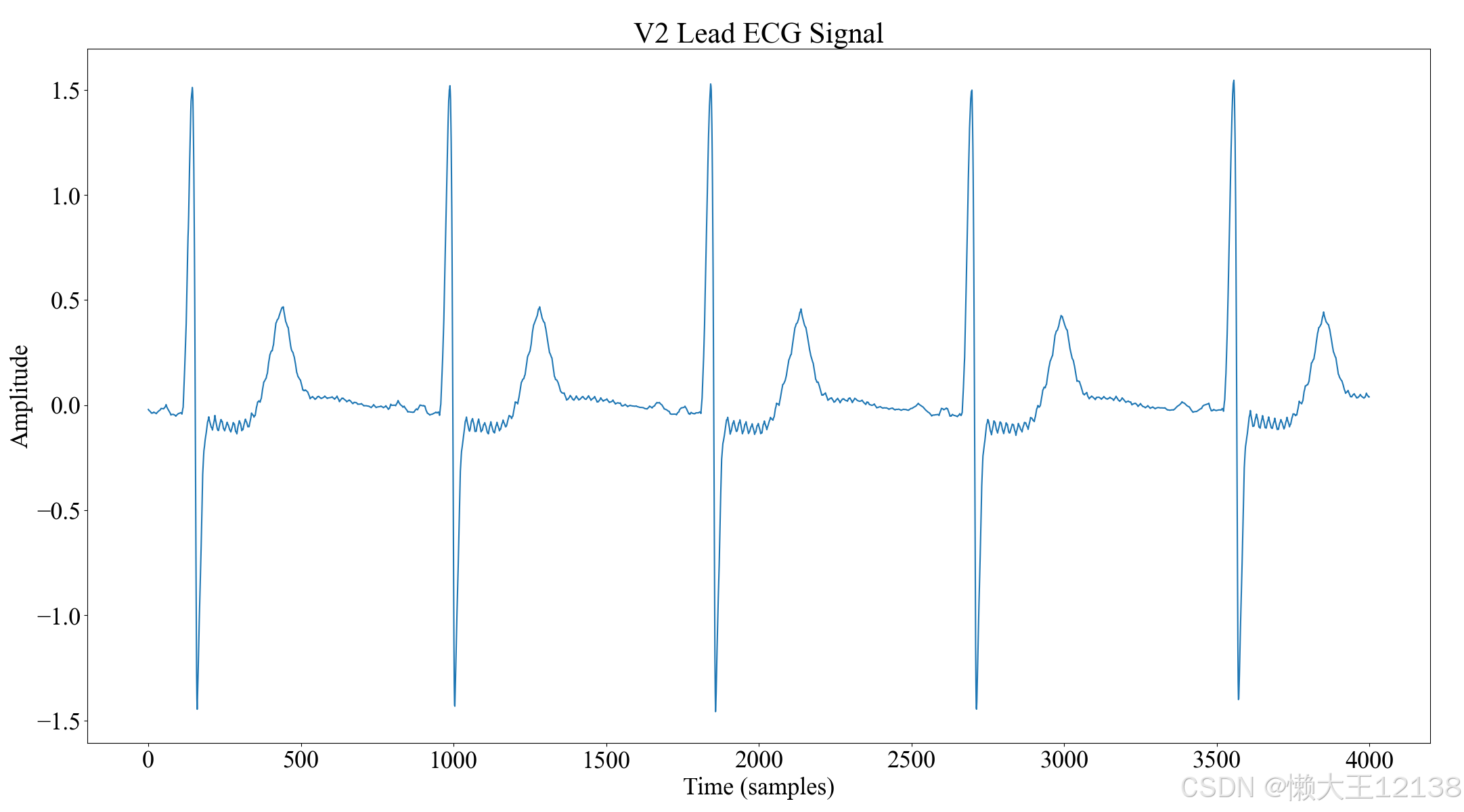
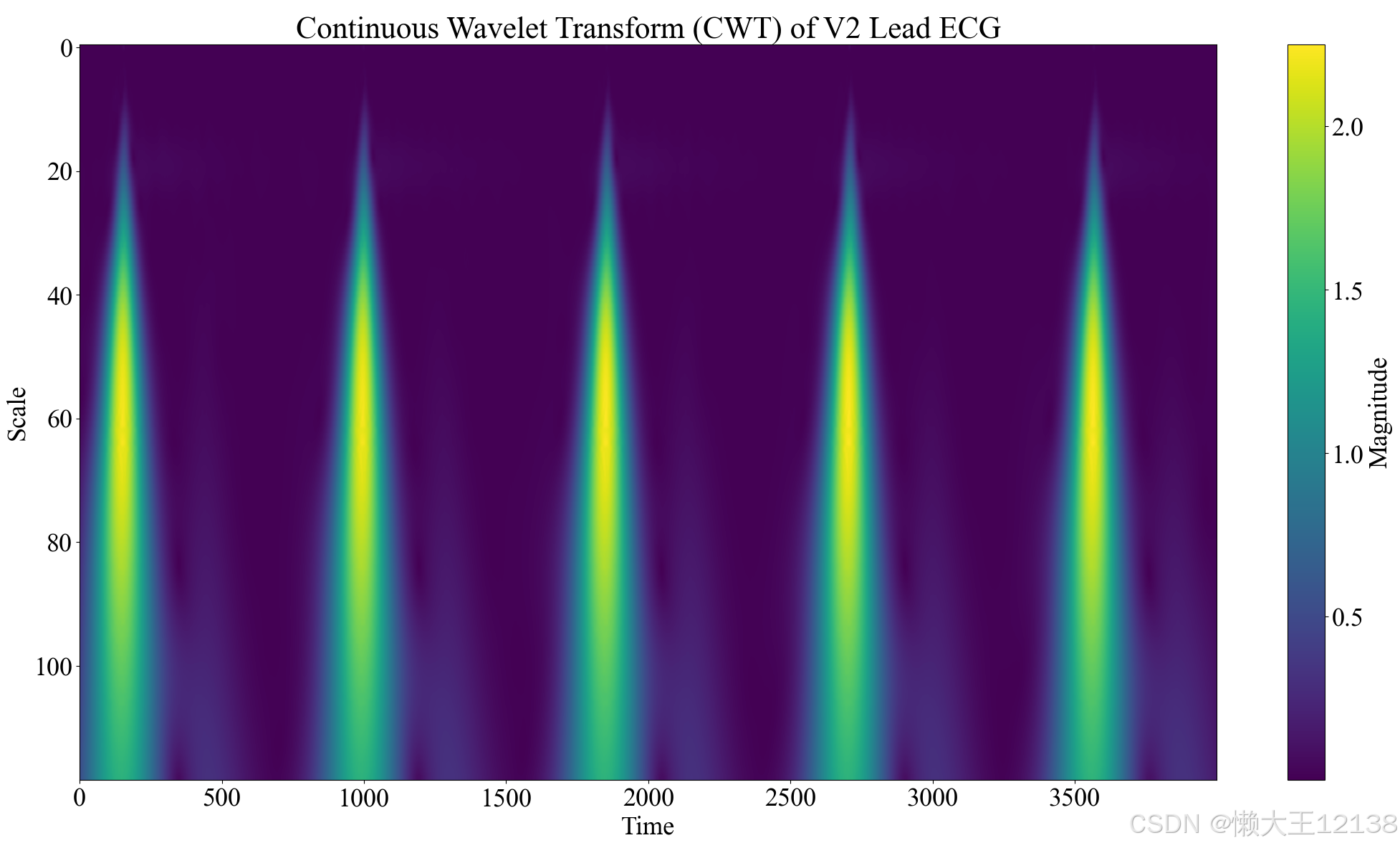
连续小波变换代码实现
import numpy as npimport matplotlib.pyplot as pltimport jsonimport pywtimport matplotlib#字体样式和大小matplotlib.rcParams['font.family'] = 'Times New Roman'matplotlib.rcParams['font.size'] = 26# 加载ECG数据,更换为自己的本地储存地址with open(r"F:\ecg segment_cwt_csdn.json", "r") as file: ecg_data = json.load(file)signal_data = ecg_data['data']#获取V2导联的数据lead_data = signal_data['V2']#定义连续小波变换def extract_cwt_features(lead_data, scales): ##cmorB-C表示带宽为B,中心频率为C的莫雷特小波; sampling_period是信号的采样频率 coefficients, frequencies = pywt.cwt(lead_data, scales, 'cmor1.5-1.0', sampling_period=1/1000) return coefficients#设置小波尺度,这里设置的尺度参数是0-119scales = np.arange(1, 120)#计算时频特征cwt_features = extract_cwt_features(lead_data, scales)#绘制处理后的CWT结果plt.figure(figsize=(12, 8))plt.imshow(np.abs(cwt_features), aspect='auto', cmap='viridis')plt.colorbar(label='Magnitude')plt.title('Continuous Wavelet Transform (CWT) of V2 Lead ECG')plt.xlabel('Time')plt.ylabel('Scale')plt.show()运行上述代码得到的时频图: