文章目录
二叉搜索树详解:基础与基本操作前言第一章:二叉搜索树的概念1.1 二叉搜索树的定义1.1.1 为什么使用二叉搜索树? 第二章:二叉搜索树的性能分析2.1 最佳与最差情况2.1.1 最佳情况2.1.2 最差情况 2.2 平衡树的优势 第三章:二叉搜索树的基本操作实现3.1 插入操作详解3.1.1 详细示例3.1.2 循环实现插入操作3.1.2.1 逻辑解析: 3.2 查找操作详解3.2.1 详细示例3.2.2 循环实现查找操作3.2.2.1 逻辑解析: 3.3 删除操作详解3.3.1 详细示例3.3.2 循环实现删除操作3.3.2.1 逻辑解析: 3.4 遍历操作详解3.4.1 中序遍历3.4.1.1 示例代码3.4.1.2 逻辑解析: 3.4.2 前序遍历3.4.2.1 示例代码3.4.2.2 逻辑解析: 3.4.3 后序遍历3.4.3.1 示例代码3.4.3.2 逻辑解析: 总结
二叉搜索树详解:基础与基本操作
? 欢迎讨论:在学习过程中,如果有任何疑问或想法,欢迎在评论区留言一起讨论。
? 点赞、收藏与分享:觉得这篇文章对你有帮助吗?记得点赞、收藏并分享给更多的朋友吧!你们的支持是我不断进步的动力!
? 分享给更多人:如果你觉得这篇文章对你有帮助,欢迎分享给更多对数据结构感兴趣的朋友,一起学习进步!
前言
二叉搜索树(Binary Search Tree, BST)是一种重要的数据结构,广泛应用于计算机科学中的数据管理和检索。它允许高效的查找、插入和删除操作,且在最佳情况下能够达到对数时间复杂度。
本文将深入探讨二叉搜索树的概念、性能分析及其基本操作,通过详细的示例和解释,帮助读者理解如何构建和操作这一数据结构。
第一章:二叉搜索树的概念
1.1 二叉搜索树的定义
二叉搜索树是一种特殊的二叉树,其具有以下特性:
节点的左子树:所有节点的值小于或等于该节点的值。节点的右子树:所有节点的值大于该节点的值。每个节点的左右子树也都是二叉搜索树。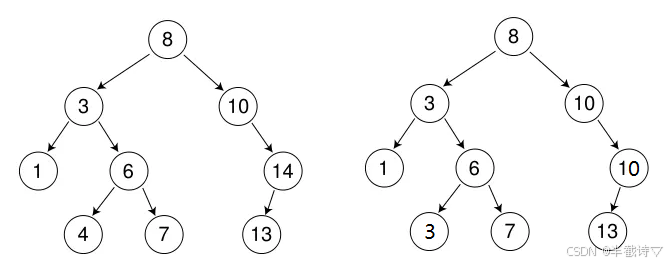
这种结构确保了我们可以有效地进行查找、插入和删除操作。
1.1.1 为什么使用二叉搜索树?
快速查找:由于节点的结构特性,查找操作可以在平均O(log N)时间内完成。动态数据支持:允许动态插入和删除数据,能够应对频繁变化的数据集。有序性:通过中序遍历,我们能够得到一个升序的序列,这对于某些算法(如排序)非常有用。 第二章:二叉搜索树的性能分析
2.1 最佳与最差情况
2.1.1 最佳情况
完全二叉树: 当树为完全平衡时,查找、插入和删除的时间复杂度均为O(log N)。例如,若插入的顺序是随机的,树可能较为平衡,此时查找、插入和删除的时间复杂度均为O(log N)。 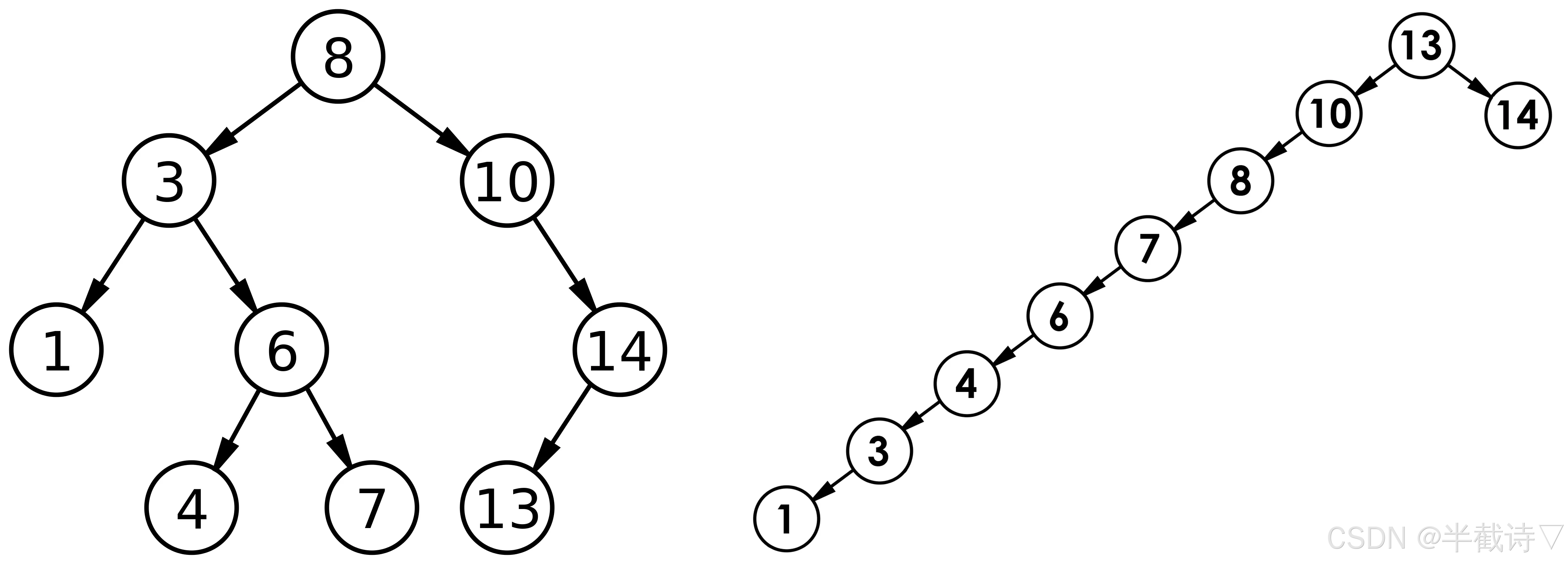
2.1.2 最差情况
退化成链表的情况: 如果数据以有序方式插入(例如:1, 2, 3, …),二叉搜索树将退化为链表,导致每次操作都需遍历整个链表,此时时间复杂度变为O(N)。 2.2 平衡树的优势
为了避免最坏情况的发生,平衡二叉树(如AVL树和红黑树)引入了旋转操作,确保在插入和删除时树的高度保持平衡。这样,在任何情况下,操作的时间复杂度均保持在O(log N)。
O(log N)的状态。 第三章:二叉搜索树的基本操作实现
3.1 插入操作详解
插入操作是构建二叉搜索树的基本步骤之一。其主要流程如下:
判断树是否为空:
如果树为空,将新节点设为根节点。这是构建树的第一步。比较并递归插入:
从根节点开始,根据节点值的大小决定向左子树还是右子树移动。找到合适位置后插入:
当找到一个空位后,将新节点插入。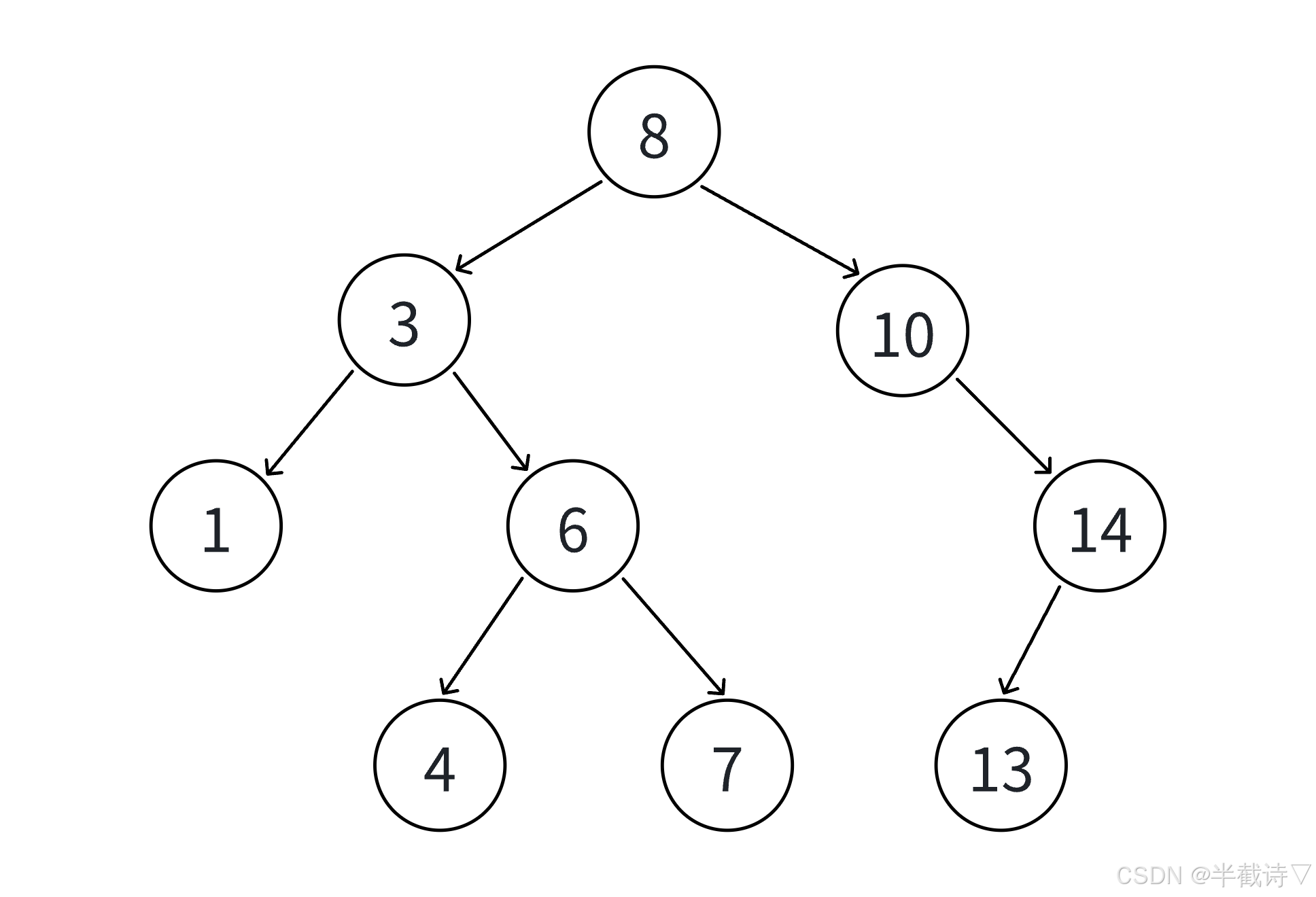
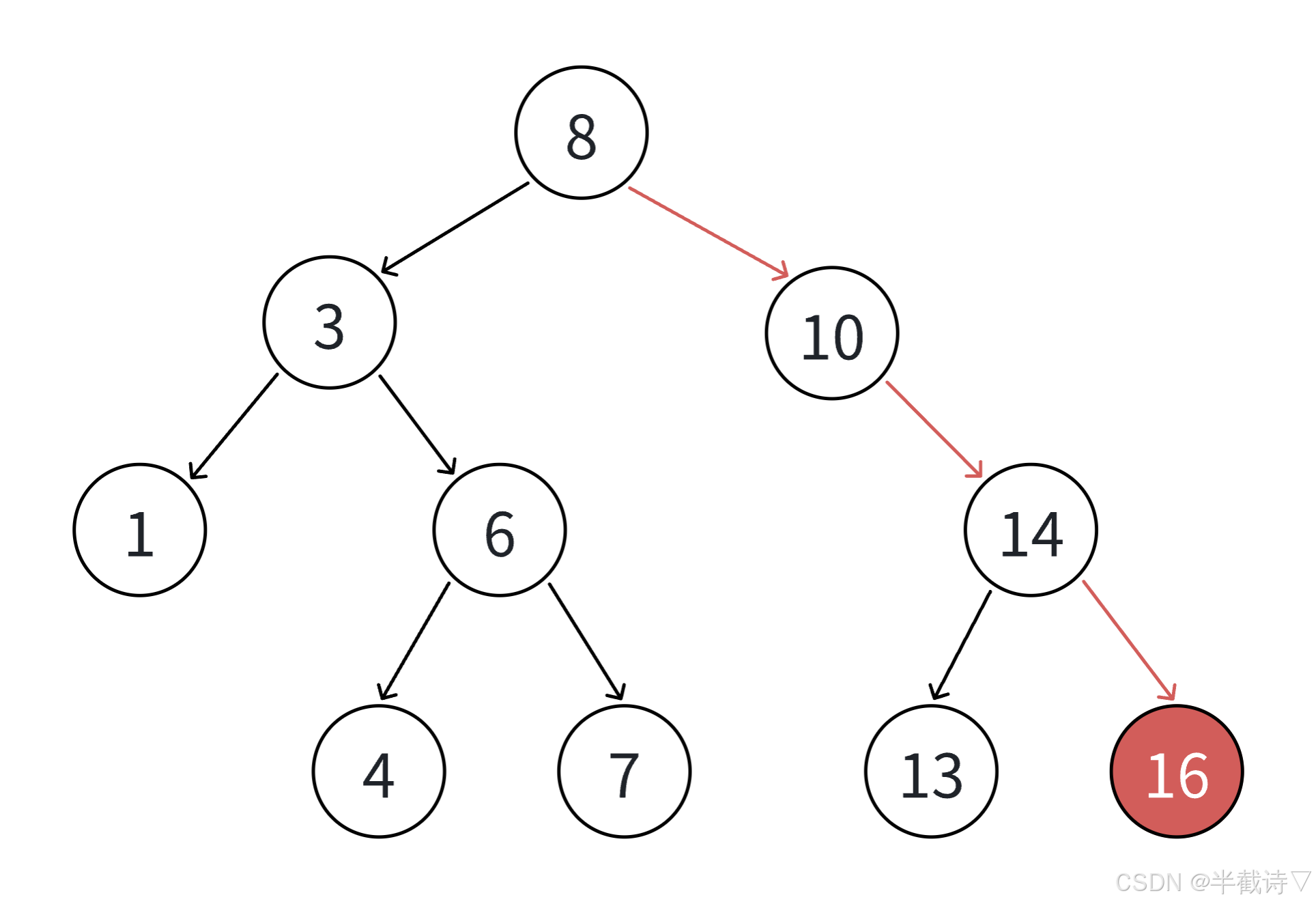
3.1.1 详细示例
让我们一步一步实现插入操作:
定义节点结构:
template<class K>class BSTNode {public: K _key; // 存储节点的值 BSTNode<K>* _left; // 左子节点 BSTNode<K>* _right; // 右子节点 BSTNode(const K& key) : _key(key), _left(nullptr), _right(nullptr) {}};定义树结构:
template<class K>class BSTree {private: BSTNode<K>* _root; // 根节点public: BSTree() : _root(nullptr) {} // 初始化树为空 bool Insert(const K& key) { if (_root == nullptr) { // 树为空 _root = new BSTNode<K>(key); // 新建根节点 return true; } return _InsertRec(_root, key); // 从根节点开始插入 }private: bool _InsertRec(BSTNode<K>* node, const K& key) { if (key < node->_key) { // 插入值小于当前节点 if (node->_left == nullptr) { // 左子节点为空 node->_left = new BSTNode<K>(key); // 创建新节点 return true; } return _InsertRec(node->_left, key); // 递归插入 } else if (key > node->_key) { // 插入值大于当前节点 if (node->_right == nullptr) { // 右子节点为空 node->_right = new BSTNode<K>(key); // 创建新节点 return true; } return _InsertRec(node->_right, key); // 递归插入 } return false; // 处理相等值的逻辑 }};3.1.2 循环实现插入操作
除了递归方式,插入操作也可以用循环实现。以下是使用循环方式的示例代码:
bool InsertIterative(const K& key) { if (_root == nullptr) { // 树为空 _root = new BSTNode<K>(key); // 新建根节点 return true; } BSTNode<K>* current = _root; BSTNode<K>* parent = nullptr; while (current != nullptr) { parent = current; // 记录父节点 if (key < current->_key) { current = current->_left; // 移动到左子节点 } else if (key > current->_key) { current = current->_right; // 移动到右子节点 } else { return false; // 找到相等值,处理逻辑 } } // 根据比较结果将新节点连接到父节点 if (key < parent->_key) { parent->_left = new BSTNode<K>(key); // 插入左子节点 } else { parent->_right = new BSTNode<K>(key); // 插入右子节点 } return true;}3.1.2.1 逻辑解析:
循环控制:使用while循环遍历树,直到找到合适的空位插入新节点。记录父节点:通过记录当前节点的父节点,以便在找到合适位置后,将新节点正确连接。 3.2 查找操作详解
查找操作使我们能够确认一个值是否存在于树中。其步骤如下:
从根节点开始比较:
判断目标值与当前节点的值大小关系。决定查找方向:
若目标值小于当前节点,则向左子树查找;若大于,则向右子树查找。终止条件:
如果找到目标值,返回成功;若当前节点为空,则说明值不存在。3.2.1 详细示例
bool Find(const K& key) { return _FindRec(_root, key); // 从根节点开始查找}private:bool _FindRec(BSTNode<K>* node, const K& key) { if (node == nullptr) return false; // 未找到 if (key == node->_key) return true; // 找到 if (key < node->_key) { return _FindRec(node->_left, key); // 向左子树查找 } else { return _FindRec(node->_right, key); // 向右子树查找 }}3.2.2 循环实现查找操作
与插入一样,查找操作也可以用循环实现。以下是循环方式的示例代码:
bool FindIterative(const K& key) { BSTNode<K>* current = _root; while (current != nullptr) { if (key == current->_key) { return true; // 找到目标值 } else if (key < current->_key) { current = current->_left; // 向左子树查找 } else { current = current->_right; // 向右子树查找 } } return false; // 未找到}3.2.2.1 逻辑解析:
循环控制:使用while循环遍历树,直至找到目标值或到达空节点。效率:循环方式避免了递归调用的开销,在处理深度较大的树时,能更有效地利用栈空间。 3.3 删除操作详解
删除操作需要考虑节点的子树情况,包括:
查找节点:首先需要找到要删除的节点。
判断情况:
没有子节点:直接删除。只有一个子节点:将父节点指向子节点。有两个子节点:选择用左子树的最大值或右子树的最小值替代删除的节点。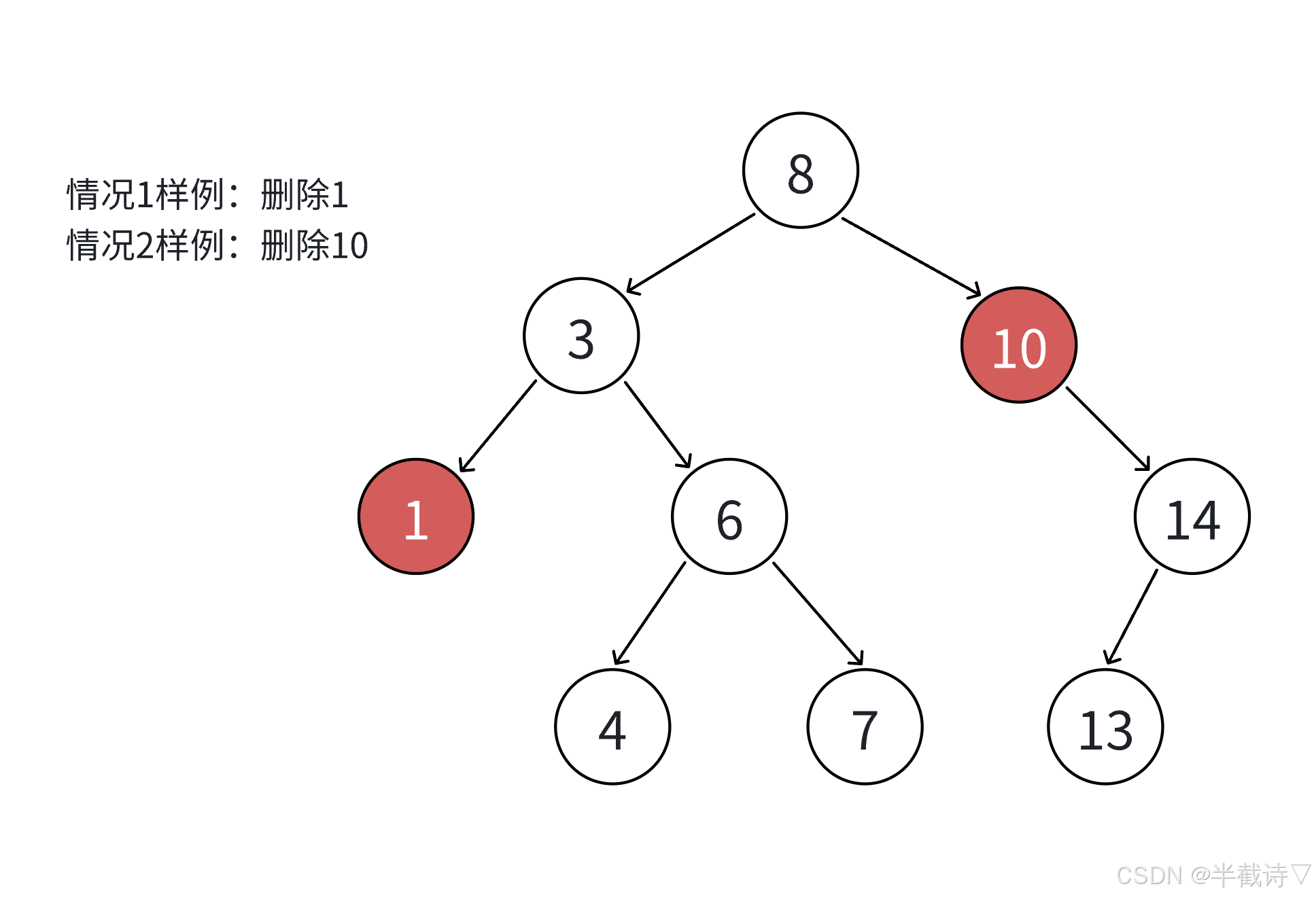
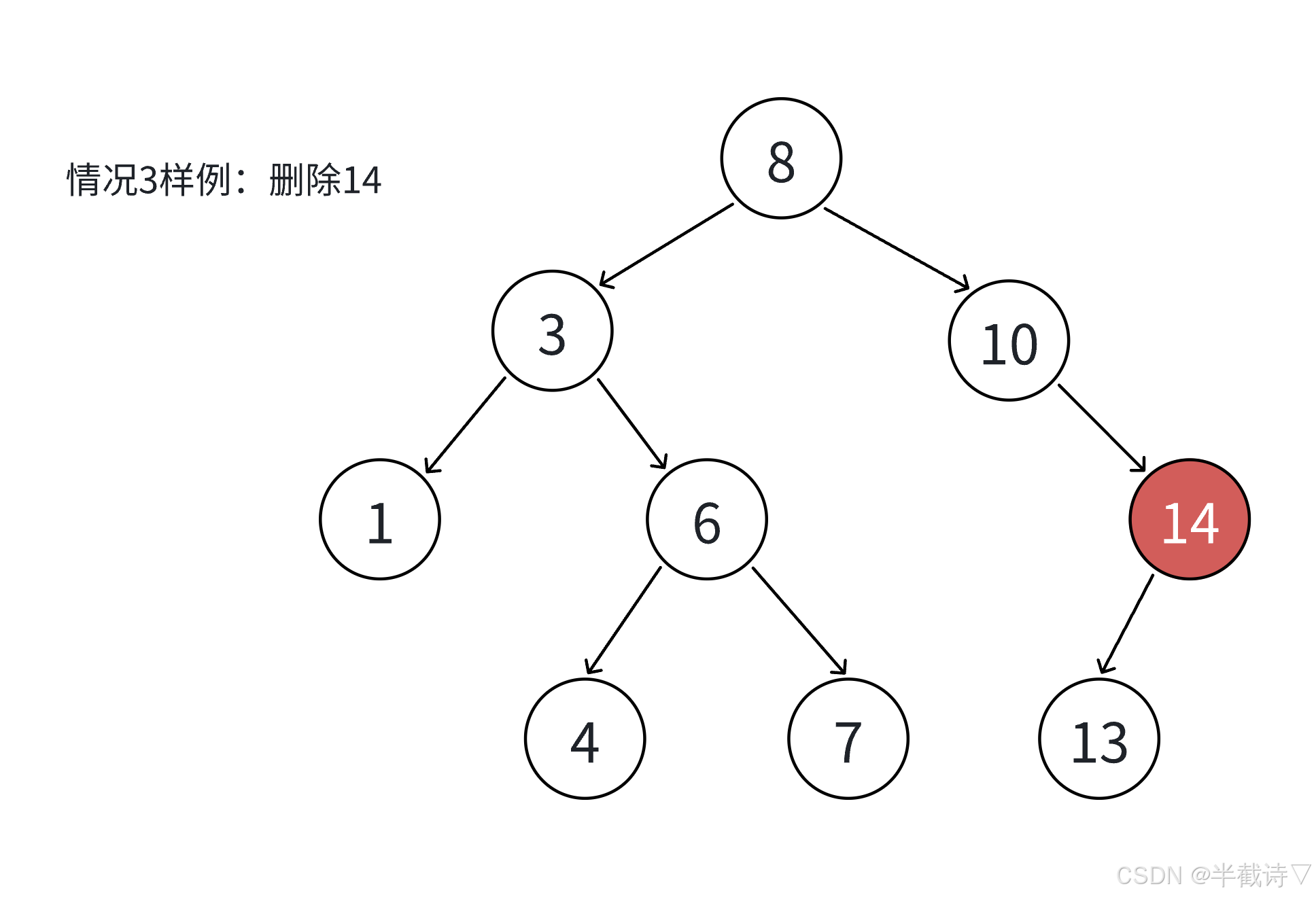
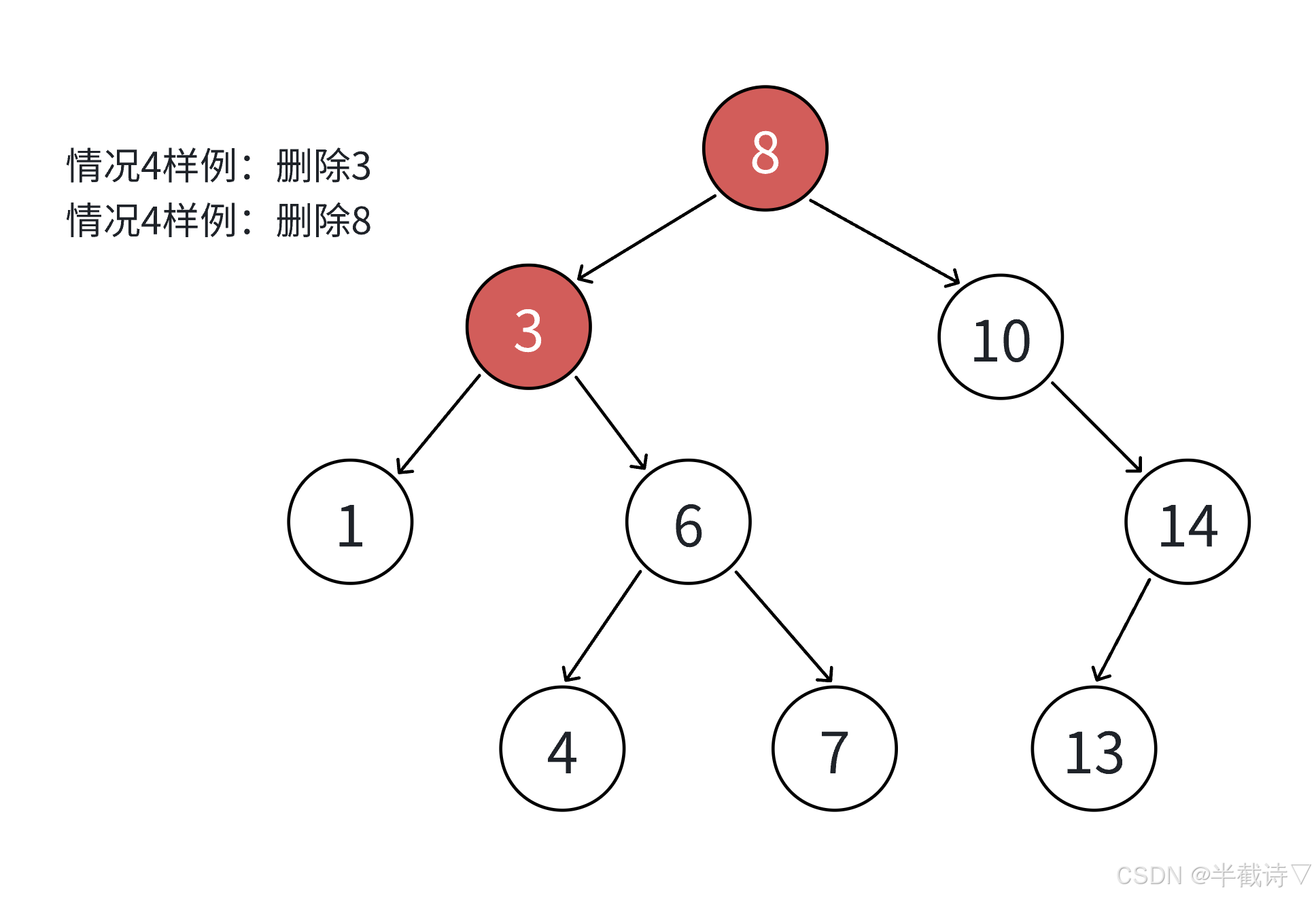
3.3.1 详细示例
bool Erase(const K& key) { return _EraseRec(_root, key); // 从根节点开始删除}private:bool _EraseRec(BSTNode<K>*& node, const K& key) { if (node == nullptr) return false; // 未找到 if (key < node->_key) { return _EraseRec(node->_left, key); // 向左子树查找 } else if (key > node->_key) { return _EraseRec(node->_right, key); // 向右子树查找 } else { // 找到要删除的节点 if (node->_left == nullptr) { BSTNode<K>* temp = node; node = node->_right; // 更新指向右子节点 delete temp; // 删除旧节点 } else if (node->_right == nullptr) { BSTNode<K>* temp = node; node = node->_left; // 更新指向左子节点 delete temp; // 删除旧节点 } else { // 找到替代节点 BSTNode<K>* temp = _FindMax(node->_left); // 左子树的最大值 node->_key = temp->_key; // 替代值 _EraseRec(node->_left, temp->_key); // 删除替代节点 } return true; }}BSTNode<K>* _FindMax(BSTNode<K>* node) { while (node->_right != nullptr) { node = node->_right; // 寻找右子树的最大值 } return node; // 返回最大节点}3.3.2 循环实现删除操作
虽然递归实现直观,但删除操作也可以用循环实现。以下是循环实现的示例代码:
bool EraseIterative(const K& key) { BSTNode<K>* current = _root; BSTNode<K>* parent = nullptr; // 找到要删除的节点和其父节点 while (current != nullptr && current->_key != key) { parent = current; if (key < current->_key) { current = current->_left; // 向左子树查找 } else { current = current->_right; // 向右子树查找 } } // 如果未找到 if (current == nullptr) return false; // 处理删除逻辑 if (current->_left == nullptr) { if (current == _root) { _root = current->_right; // 更新根节点 } else if (parent->_left == current) { parent->_left = current->_right; // 更新父节点的左指针 } else { parent->_right = current->_right; // 更新父节点的右指针 } } else if (current->_right == nullptr) { if (current == _root) { _root = current->_left; // 更新根节点 } else if (parent->_left == current) { parent->_left = current->_left; // 更新父节点的左指针 } else { parent->_right = current->_left; // 更新父节点的右指针 } } else { // 找到替代节点 BSTNode<K>* successor = _FindMin(current->_right); // 右子树的最小值 K successorKey = successor->_key; // 备份替代值 EraseIterative(successorKey); // 递归删除替代节点 current->_key = successorKey; // 替代当前节点的值 } delete current; // 删除当前节点 return true;}BSTNode<K>* _FindMin(BSTNode<K>* node) { while (node && node->_left != nullptr) { node = node->_left; // 寻找左子树的最小值 } return node; // 返回最小节点}3.3.2.1 逻辑解析:
查找节点:通过循环查找要删除的节点及其父节点。处理删除逻辑:根据节点的子树情况,选择合适的删除策略。更新指针:确保在删除节点后,正确更新父节点的指向,保持树的完整性。3.4 遍历操作详解
遍历操作是对二叉搜索树进行全面访问的方式,通常分为三种基本类型:前序遍历、中序遍历和后序遍历。每种遍历都有其特定的应用场景。
3.4.1 中序遍历
中序遍历(左-根-右)会按顺序输出树中的节点值,使得遍历结果是一个升序序列。
步骤:
先访问左子树。然后访问根节点。最后访问右子树。3.4.1.1 示例代码
void InOrderTraversal(BSTNode<K>* node) { if (node == nullptr) return; // 如果节点为空,返回 InOrderTraversal(node->_left); // 递归访问左子树 cout << node->_key << " "; // 访问当前节点 InOrderTraversal(node->_right); // 递归访问右子树}3.4.1.2 逻辑解析:
递归方式:此方法通过递归访问每个节点,确保按顺序访问。输出顺序:中序遍历确保了节点值的升序排列,对于排序需求非常有用。3.4.2 前序遍历
前序遍历(根-左-右)常用于复制树结构,因为它先访问根节点。
步骤:
先访问根节点。然后访问左子树。最后访问右子树。3.4.2.1 示例代码
void PreOrderTraversal(BSTNode<K>* node) { if (node == nullptr) return; // 如果节点为空,返回 cout << node->_key << " "; // 访问当前节点 PreOrderTraversal(node->_left); // 递归访问左子树 PreOrderTraversal(node->_right); // 递归访问右子树}3.4.2.2 逻辑解析:
根节点优先:此方法适合在需要先处理根节点的场景,例如在构建其他数据结构时。结构复制:前序遍历有助于复制树结构,因为它提供了节点的先后顺序。3.4.3 后序遍历
后序遍历(左-右-根)常用于删除树的节点,因为它先访问子节点。
步骤:
先访问左子树。然后访问右子树。最后访问根节点。3.4.3.1 示例代码
void PostOrderTraversal(BSTNode<K>* node) { if (node == nullptr) return; // 如果节点为空,返回 PostOrderTraversal(node->_left); // 递归访问左子树 PostOrderTraversal(node->_right); // 递归访问右子树 cout << node->_key << " "; // 访问当前节点}3.4.3.2 逻辑解析:
子节点优先:后序遍历确保在删除节点之前,先处理它的子节点。这种策略在清空树时非常重要。删除操作:通常用在需要在树结构被修改前完成所有子树处理的场景。总结
在这篇博客中,我们如同探险者,走进了二叉搜索树的奥秘世界,揭示了这一数据结构背后的智慧。二叉搜索树不仅是一种高效的数据存储与检索方式,更是算法与结构之美的结合。通过插入、查找和删除操作的细致分析,我们看到了效率与灵活性的完美平衡。
中序遍历所展现的有序之美、前序遍历的根节点优先以及后序遍历的从容处理,犹如乐章中的不同乐器,共同演绎出数据处理的交响曲。二叉搜索树不仅帮助我们优化程序性能,更启示我们在面对复杂问题时,保持思维的清晰与结构的严谨。
在这个快速发展的技术时代,掌握二叉搜索树的精髓,将使我们在数据的海洋中游刃有余。未来的学习旅程将更加丰富,二叉搜索树将继续为我们提供无尽的启示与灵感。
? 讨论区:如果你有任何问题,欢迎在评论区留言讨论!
? 支持一下:如果你觉得这篇文章对你有帮助,请点赞、收藏并分享给更多学习者!
以上就是关于【C++篇】数据之林:解读二叉搜索树的优雅结构与运算哲学的内容啦,各位大佬有什么问题欢迎在评论区指正,或者私信我也是可以的啦,您的支持是我创作的最大动力!❤️
