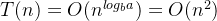一、棋盘覆盖-设计规则
在一个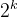 ×
×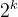 个方格组成的棋盘中,恰有一个方格与其他方格不 同,称该方格为“特殊方格”,且称该棋盘为“特殊棋盘”,在棋盘覆盖问题中,要用图1所示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
个方格组成的棋盘中,恰有一个方格与其他方格不 同,称该方格为“特殊方格”,且称该棋盘为“特殊棋盘”,在棋盘覆盖问题中,要用图1所示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
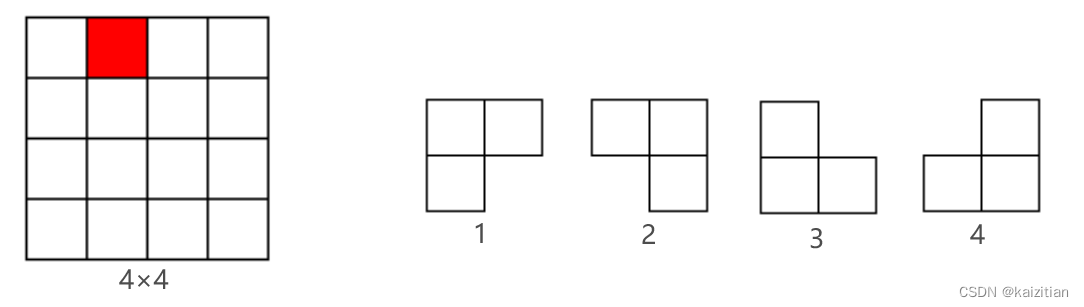
图1
二、棋盘覆盖-设计思路
棋盘覆盖采用的是分治法,分而治之。当k>0时,将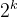 ×
×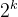 棋盘分割为4个
棋盘分割为4个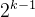 ×
×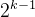 子棋盘,例如图1中4×4的棋盘,将其分割成4个2×2的子棋盘,如2图所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了 将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3 个较小棋盘的会合处,如图3所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1。
子棋盘,例如图1中4×4的棋盘,将其分割成4个2×2的子棋盘,如2图所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了 将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3 个较小棋盘的会合处,如图3所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1。
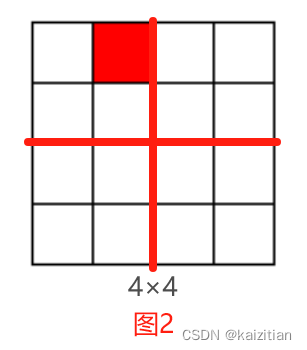
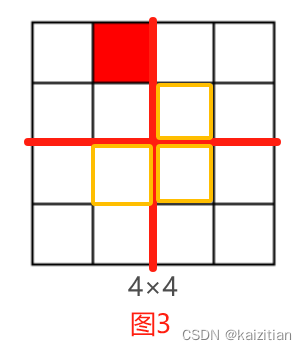
4个较小规模的棋盘问题,4个子问题规模一样,但是处理方式不一样的子问题:
左上角子问题:判断特殊方格是否在此棋盘中;如果是在此棋盘,则对此棋盘进行递归调用;如果不在此棋盘,则用t号骨牌覆盖右下角,然后再对此棋盘进行递归调用。
左下角子问题:判断特殊方格是否在此棋盘中;如果是在此棋盘,则对此棋盘进行递归调用;如果不在此棋盘,则用t号骨牌覆盖右上角,然后再对此棋盘进行递归调用。
右上角子问题:判断特殊方格是否在此棋盘中;如果是在此棋盘,则对此棋盘进行递归调用;如果不在此棋盘,则用t号骨牌覆盖左下角,然后再对此棋盘进行递归调用。
右下角子问题:判断特殊方格是否在此棋盘中;如果是在此棋盘,则对此棋盘进行递归调用;如果不在此棋盘,则用t号骨牌覆盖左上角,然后再对此棋盘进行递归调用。
三、棋盘覆盖-设计代码
//C语言#include <stdio.h>int Tile = 1; //全局变量骨牌号int Board[100][100]; //全局数组//棋盘覆盖void ChessBoard(int Tr, int Tc, int Dr, int Dc, int Size){ //Tr表示棋盘左上角的行号,Tc表示棋盘左上角的列 //Dr表示棋盘特殊方格的行号,Dc表示棋盘特殊方格的列号 //Size表示棋盘的宽 if(Size == 1) return; int t = Tile++; //L型牌骨号 int s = Size/2; //割分棋盘 //覆盖左上角的子棋盘 if(Dr < Tr + s && Dc < Tc + s){ //说明特殊方格在此棋盘中 ChessBoard(Tr,Tc,Dr,Dc,s); } else{ //说明特殊方格不在此棋盘中 //需要用t号L型骨牌覆盖右下角 Board[Tr+s-1][Tc+s-1] = t; ChessBoard(Tr,Tc,Tr+s-1,Tc+s-1,s); } //覆盖右上角的子棋盘 if(Dr < Tr + s && Dc >= Tc+s){ //说明特殊方格在此棋盘中 ChessBoard(Tr,Tc + s, Dr, Dc, s); } else{ //说明特殊方格不在此棋盘中 //需要用t号L型骨牌覆盖左下角 Board[Tr+s-1][Tc+s] = t; ChessBoard(Tr,Tc+s,Tr+s-1,Tc+s,s); } //覆盖左下角的子棋盘 if(Dr >= Tr + s && Dc < Tc + s){ //说明特殊方格在此棋盘中 ChessBoard(Tr+s,Tc,Dr,Dc,s); } else{ //说明特殊方格不在此棋盘中 //需要用t号L型骨牌覆盖右上角 Board[Tr+s][Tc+s-1] = t; ChessBoard(Tr+s,Tc,Tr+s,Tc+s-1,s); } //覆盖右下角的子棋盘 if(Dr >= Tr + s && Dc >= Tc + s){ //说明特殊方格在此棋盘中 ChessBoard(Tr+s,Tc+s,Dr,Dc,s); } else{ //说明特殊方格不在此棋盘中 //需要用t号L型骨牌覆盖左上角 Board[Tr+s][Tc+s] = t; ChessBoard(Tr+s,Tc+s,Tr+s,Tc+s,s); }}//打印数组void Func1(int Array[100][100], int Size){ int i,j; for(i=0;i<Size;i++){ for(j=0;j<Size;j++){ printf("%d\t",Array[i][j]); } printf("\n"); }}//计算数组的Size:例如k=2,则Size为4,故矩阵为4*4int Func2(int k){ int sum = 1; int i; for(i = 0; i < k; i++){ sum = sum * 2; } return sum;}int main(){ int a = 0; int b = 0; int k = 0; int Size = 0; printf("请输入棋盘大小k(注:大小是2^k*2^k):"); scanf("%d",&k); printf("输出k=%d:\n",k); Size = Func2(k); printf("输出Size=%d:\n",Size); printf("请输入特殊方格的位置:"); scanf("%d,%d",&a,&b); Board[a][b] = 0; ChessBoard(0,0,a,b,Size); Func1(Board,Size); return 0;}运行结果
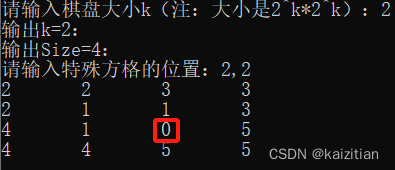
四、棋盘覆盖-时间复杂性分析
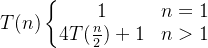
Master定理方法 :
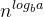

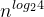

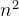 ,
,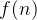

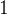

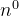
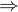
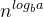
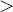
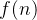
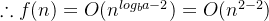 ,
,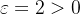
 根据Master定理规则1:
根据Master定理规则1: