数据科学学习之探索性数据分析（EDA）_初飞墨的博客

前言

本文为笔者学习图灵系列程序设计丛书的《面向数据科学家的使用统计学》的一些感悟和总结，本文撰写主要参考了该书目，希望本文对接触，学习和研究数据科学的各位能有所帮助。
首先，第一篇介绍探索性数据分析（EDA）的相关内容。

1.什么是结构化数据

在现代，尤其是这个大数据时代，我们获取数据的途径非常丰富，各种仪器（例如各种传感器）的测量值、事件、文本、图像和视频等都属于可获取的数据来源，整个物联网无时无刻不在涌出大量的信息流。如何将这些大量的原始数据转化为可操作的信息，这才是当今数据科学所面对的主要挑战。首先，就需要将非结构化的原始数据结构化，或是处于研究目的采集有效数据集。

结构化数据有两种基本类型：数值型数据(numeric data)和分类数据(categorical data)。其中，数值型数据还分为连续型和离散型两种形式，连续型数据又称区间数据和浮点型数据，即表示该数据可在一个区间内取任何值；离散型数据通常只能取整数，例如计数，所以一般又称计数型数据。分类数据（因子数据）只能从特定集合中取值，这些值表示这种数据一系列可能的分类，例如：计算机编程语言主要包括汇编语言、机器语言以及高级语言三种（类别）；中国的直辖市有北京市，上海市，天津市和重庆市。二元数据是一种特殊的分类数据，数据值只能从两个之中取其一（例如0或1，True或False），也就是一般所称的布尔型数据和逻辑性数据。有序数据（有序因子数据）是具有明确排序的分类数据，例如数值排序（1，2，3，4或5）。

注：连续型数据和离散型数据的区别：1.离散型变量是通过计数方式取得的，即是对所要统计的对象进行计数，增长量非固定的；连续型变量不是单独的整十整百的数字，其包含若干位小数且取值密集，增长量可以划分为固定的单位。2.域不同。离散型变量：离散型变量的域(即对象的集合)是离散的；连续型变量的域(即对象的集合)是连续的。3.分组方式不同。离散型变量：如果变量值的变动幅度小，就可以一个变量值对应一组，称单项式分组。如果变量值的变动幅度很大，变量值的个数很多，则把整个变量值依次划分为几个区间，各个变量值则按其大小确定所归并的区间，区间的距离称为组距，这样的分组称为组距式分组，在组距式分组中，相邻组既可以有确定的上下限，也可将相邻组的组限重叠。连续型变量：连续型变量由于不能一一列举其变量值，只能采用组距式的分组方式，且相邻的组限必须重叠。

• 我们为什么要关心数据类型的分类呢？
  首先，数据类型对于确定可视化类型、数据分析或统计模型是非常重要的。再者，更为重要的是，变量的数据类型决定了软件处理变量计算的方法。
• 因子数据或说有序因子数据也只是一组文本值或数值，那么为什么我们也需要在数据分析种明确提出它们的概念呢？
  相比于文本表示，将数据显示地标识为因子数据具有如下优点：
• 如果我们明确输入的是分类数据，那么软件就可以据此确定统计过程的工作方式，例如图表生成或模型拟合。
• 可以优化存储或索引。
• 限定了给定分类变量在软件中的可能取值，例如枚举类型。

总结：

• 在软件中，数据通常按类型分类。
• 数据类型包括连续型数据、离散型数据、分类数据和有序数据。
• 数据分类为软件指明了数据的处理方式。

2.矩形数据

矩形数据对象是数据科学分析中的典型引用结构，矩形数据对象包括电子表格、数据库表等。
矩形数据本质上是一个二维矩阵，通常称数据表中的一行为一条记录（事例、样本），一列为一个特征（属性、变量）。数据并非一开始就是矩阵形式的，非结构化数据必须先经过处理和操作才能表示为矩阵数据形式。
除了矩形数据之外，还有一些其它类型的数据：例如：时序数据，空间数据和图形（或网络）数据。（此处的空间和图形同矩形一样，均指一种数据结构。）

3.位置估计

面对大量数据的记录和特征，对它们有一个大致的了解，即总结数据特征的特性是很有必要的。其中，探索数据的一个基本步骤就是获取每个特征的“典型值”，典型值是指对数据最常出现位置的估计，即数据的集中趋势。

平均值(mean)，是最基本的位置估计量，它等于所有值的和除以值的个数，给出计算公式：
x ˉ = Σ i = 1 n x i n \bar x=\frac{\Sigma_{i=1}^n x_i} n xˉ=nΣi=1n​xi​​
对于某些数据集，我们需要对值赋予权重，进行位置估计时便需取加权均值(weighted mean)，它等于加权值的总和除以权重的总和，给出计算公式：
x ˉ w = Σ i = 1 n w i x i Σ i = 1 n w i \bar x_w=\frac{\Sigma_{i=1}^n w_ix_i}{\Sigma_{i=1}^n w_i} xˉw​=Σi=1n​wi​Σi=1n​wi​xi​​
均值虽然易于计算且方便使用，但在数据集中有离群值（极值）影响时便无法较为准确地进行位置估计，此时，中位数(median)是更好的选择。中位数是位于有序数据集中间位置的数值，是对位置更为稳健的估计量，但不同于使用所有观测值计算得到的均值，中位数仅取决于有序数据集中间位置处的值。与加权均值相似，加权中位数(weighted median)也有广泛的应用，它使得排序数据集中分别有一半的权重之和位于该值之上或之下。

若想尽可能使用所有观测值对位置有一个较为稳健的估计，我们可以使用切尾均值(trimmed mean)。它是指在数据集剔除一定数量的极值后再求均值，这样就能消除极值对均值的影响，例如在国际体育赛事中，通常会去掉一个最高分和一个最低分，就是使用了切尾均值。给出计算公式：
x ˉ = Σ i = p + 1 n − p x i n − 2 p \bar x=\frac{\Sigma_{i=p+1}^{n-p} x_i}{n-2p} xˉ=n−2pΣi=p+1n−p​xi​​
对于小规模的数据集，还有很多其他更为稳健和高效的位置估计量，在此不做介绍。

4.变异性估计

位置只是总结特性的一个维度，另一个维度是变异性(variability)，也称离差（dispersion)，它是数据集关于某个中心值偏离或散布的离散程度的一种标志，测量了数据值是紧密聚集的还是发散的。使用最广泛的变异性估计量是基于位置估计值和观测数据值之间的偏差(deviation)或者说残差(residual)，在这里，给出多种计算偏差的方式。

首先是平均绝对偏差(mean absolute deviation)，即对数据值和均值之间的偏差的绝对值计算均值。给出公式:
平 均 绝 对 偏 差 = Σ i = 1 n ∣ x i − x ˉ ∣ n − 2 p 平均绝对偏差=\frac{\Sigma_{i=1}^n \lvert x_i-\bar x \rvert}{n-2p} 平均绝对偏差=n−2pΣi=1n​∣xi​−xˉ∣​
更广为人知的变异性估计量是方差(variance)和标准偏差(standard deviation)，它们基于偏差的平方。方差是偏差平方值的均值，而标准偏差是方差的平方根。给出公式：
方 差 = s 2 = Σ ( x − x ˉ ) 2 n − 1 方差=s^2=\frac{\Sigma (x-\bar x)^2}{n-1} 方差=s2=n−1Σ(x−xˉ)2​
标 准 偏 差 = s = Σ ( x − x ˉ ) 2 n − 1 标准偏差=s=\sqrt\frac{\Sigma (x-\bar x)^2}{n-1} 标准偏差=s=n−1Σ(x−xˉ)2​ ​

注：在统计模型中，使用平方值比使用平均值更为方便，所以标准偏差比平均绝对偏差使用更为广泛，而式中使用除数n-1是因为我们使用自由度进行无偏估计。

无论是方差，标准偏差还是绝对平均偏差对离群值都是不稳建的，尤其是方差和标准偏差对极值更为敏感，为此，我们提出更为稳健的变异性估计量，中位数绝对偏差(median absolute deviation)，通常简写为MAD。给出计算公式：
M A D = 中 位 数 ( ∣ x 1 − m ∣ , ∣ x 2 − m ∣ , … , ∣ x n − m ∣ ) MAD=中位数(\lvert x_1-m \rvert,\lvert x_2-m \rvert,…,\lvert x_n-m \rvert) MAD=中位数(∣x1​−m∣,∣x2​−m∣,…,∣xn​−m∣)
我们还可以参考切尾均值计算切尾标准偏差。

注：即使数据符合正态分布，方差、标准偏差、平均绝对偏差以及中位数绝对偏差也并非是等价的估计量。事实上，标准偏差总是大于平均绝对偏差，而平均绝对偏差总是大于中位数绝对偏差。有时，中位数绝对偏差会乘上一个常数比例因子（通常是1.4826），使得在正态分布下，中位数绝对偏差与标准偏差具有相同的尺度。

另一种估计离差的方法基于对有序数据分布情况的查看。其中最基本的是测量极差(range)，或称为全距，但极差对离群值非常敏感，为避免这种情况，我们可以删除有序数据两端的值，然后再查看数据的极差，即估计百分位数(percentiles)之间的差异。其中常用的测量方法是估计第25分位数和第75分位数之间的差值，称为四分位距(interquartile range, IQR)，在此不做过多介绍。

5.探索数据分布

5.1 百分位数和箱形图

百分位数对于总结数据的整体分布十分有用，四分位数和十分位数有着广泛的应用，尤其是在总结数据尾部情况（外延范围）时，百分位数十分有用。

箱形图(boxplot)是一种快速可视化绘图，它基于百分位数来可视化数据的分布，能显示出一组数据的最大值、最小值、中位数、及上下四分位数。

import numpy as np
import pandas as pd
data=pd.Series(np.arange(0,16)).append(pd.Series(25))
data.plot(kind='box')

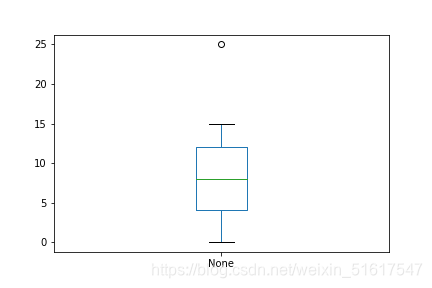
使用python绘出一个简单的箱形图，其中，箱子的顶部和底部分别是第75百分位数和第25百分位数。箱内的水平线表示的是中位数。从箱顶或箱底延伸的线段称为须(whisker)，须从最大值一直延伸到最小值，显示了数据的极差，而箱外的圈（或说点）表示的则是离群值。

5.2 频数表和直方图

变量（特征）的频数表可以将该变量的极差均匀地分割为多个等距分段，并给出落在每个分段中地数值个数。

import numpy as np
import pandas as pd
data=pd.Series(np.random.rand(10))
data.plot(kind='hist')

使用python绘出一个简单的直方图，可以观察到其中有两个组距是空的，添加空组距也是有必要的，空组距中没有值通常是很有价值的信息。尝试不同大小的组距也是非常有用的，如果组距过大，可能就会隐藏掉分布的一些重要特性；如果组距过小，那么结果就会过于颗粒化，失去查看整体图的能力。

绘制直方图需注意：1.空组距也应在直方图中。2.各组距是相等的。3.组距的数量（或组距的大小）是自定的。4.各条块相互紧邻，条块间没有任何空隙，除非存在空组距。

注：频数表和百分位数都是通过创建组距总结数据。一般情况下，四分位数和十分位数在每个组距中具有相同的计数，但每个组距的大小不同，将其称之为等计数组距，相反地，频数表中每个组距的大小相同，但其中的计数可以不同，将其称之为等规模组距。
统计学中的矩（moment）：在统计学理论中，位置和变异性分别称为分布的一阶矩和二阶矩，而分布的三阶矩和四阶矩分别被称为偏度(skewness)和峰度(kurtosis)。偏度显示了数据是偏向较小的值还是较大的值；峰度则显示了数据中具有极值的倾向性。通常情况下，我们不使用度量去测定偏度和峰度，而是通过可视化方法来发现他们。

5.3 密度估计

密度图用一条连续的线显示数据值的分布情况。可以将密度图看作由直方图平滑得到的，尽管它通常是使用一种核密度估计量从数据中直接计算得到的。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data=pd.Series(np.random.normal(0, 1, 1000))
plt.figure()
plt.subplots_adjust(wspace=0.2)
plt.subplot(1,2,1)
data.plot(kind='hist',bins=14,density=True)
data.plot(kind='kde')
plt.xlim(-4,4)
plt.subplot(1,2,2)
data.plot(kind='kde')
plt.xlim(-4,4)
plt.rcParams['figure.figsize']=(12.0,4.0)

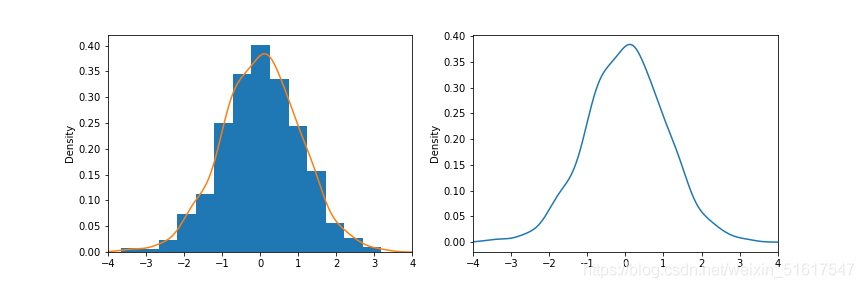
使用python绘出一个正态分布数值集的密度图和直方图的情况，可清晰的看出核密度图与直方图之间的关系，而当数据量越大时，核密度图和直方图平滑得到的曲线越相似。

data=pd.Series(np.random.normal(0, 1, 100)) #右图为data=pd.Series(np.random.normal(0, 1, 10000))
y=data.plot(kind='hist',bins=14,density=True,alpha=0.3,label='hist')
data.plot(kind='kde',label='kde')
plt.plot(np.arange(-3.6,4,0.4)-0.2,frequency_each,label='hist_line')
plt.xlim(-4,4)
plt.legend()
plt.show()

如图，分别为选取100个数据和10000个数据核密度图与取直方图组距中点的值得到的平滑曲线拟合的情况。

6.探索分类数据

6.1 众数和期望值

众数是数据集中出现次数最多的类别或值，是分类数据的一个基本汇总统计量，通常不用于数值型数据。

有些数据类别可以表示成或映射到同一尺度的离散值，也就是可以与一系列的数值相关联，那么就可以根据类别出现的概率计算出一个平均值，称之为期望值，它是一种加权均值，权重使用的是类别出现的概率。

6.2 条形图和饼图

条形图和饼图是常用来可视化分类数据的方法，条形图以条形表示每个类别出现的频数或占比情况，饼图是条形图的一种替代形式，以圆饼中的一个扇形部分表示每个类别出现的频数或占比情况。

要特别注意的是，虽然条形图与直方图非常相似，但二者之间仍存在着一些差异。在条形图中，x轴表示因子变量的不同类别，而在直方图中，x轴以数值度量的形式表示某个变量的值。另外，在直方图中，通常各个条形是相互紧邻的，条形间的间隔表示空组距（即数据中未出现的值），而在条形图中，各个条形的显示是相互独立的。

data=pd.Series(np.random.randint(1,11,20))
data.plot(kind='bar')
data.plot(kind='pie')

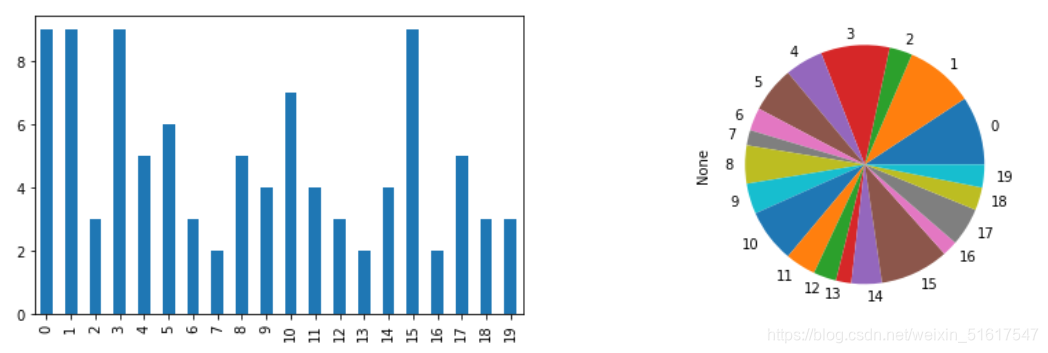
使用python绘出一些离散变量的条形图和饼图。

7.相关性

相关性，是指两个变量的关联程度。无论是在数据科学还是研究中，很多建模项目的探索性数据分析都要检查预测因子之间的相关性，以及预测因子和目标变量之间的相关性。

如果一个变量的高值随另一个变量的高值的变化而变化，并且它的低值随另一个变量的低值的变化而变化，那么称这两个变量正相关。如果一个变量的高值随另一个变量的低值的变化而变化，且反之亦然，那么称这两个变量负相关。如果一个变量的变化对另一变量没有明显影响，那么称这两个变量不相关。

首先介绍三个重要概念：

1. 相关系数(Correlation coefficient)：一种标准化的度量，用于测量数值变量之间的相关程度，取值范围在-1（完全负相关）和+1（完全正相关）之间。若其值为0，则表示两个变量之间没有相关性，需注意，数据的随机排列将会随机生成正的或负的相关系数。
2. 相关矩阵(Correlation Matrix)：将变量在一个表格中按行和列显示，表格中每个单元格的值是对应变量之间的相关性。
3. 散点图(scatter-plot)：在绘图中，x轴表示一个变量（特征）的值，y轴表示另一个变量的值，可以反映出y随x的变化而变化的大致趋势。

7.1 相关系数

皮尔逊相关系数公式：
r = Σ i = 1 N ( x i − x ˉ ) ( y i − y ˉ ) ( n − 1 ) s x s y r=\frac{\Sigma_{i=1}^ N{(x_i-\bar x)(y_i-\bar y)}}{(n-1)s_xs_y} r=(n−1)sx​sy​Σi=1N​(xi​−xˉ)(yi​−yˉ​)​
当变量的相关性是非线性的时候，相关系数就不再是一种有用的度量，此时需计算非线性相关系数来对变量的相关性来做出判断。而反映一个因变量与一组自变量(两个或两个以上)之间相关程度的指标称为复相关系数，在此不做过多介绍。

7.2 相关矩阵

在可视化方法上，我们可以使用热力图（见8.1.1）来可视化相关矩阵。

import seaborn as sns
import warnings
warnings.filterwarnings("ignore") 
from pyforest import *
wine=pd.read_csv('wine.csv')
corr = wine.corr() #相关矩阵计算方法
fig, ax = plt.subplots(figsize=(16, 12))
ax = sns.heatmap(corr,square=True,ax=ax,annot=True)
ax.set_title('Correlation coefficient')

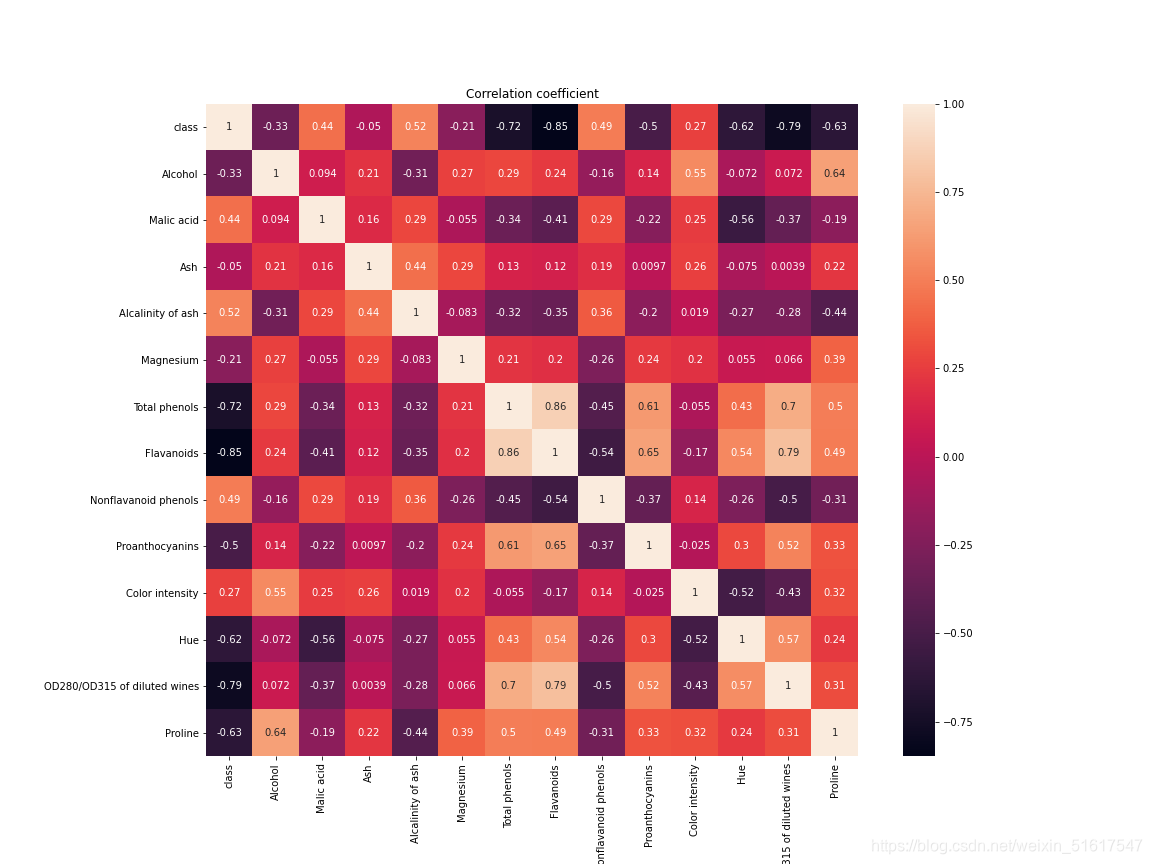
以sklearn库中的wine数据集（笔者使用时已将数据集导入到了csv文件中）为例，计算该数据集各变量（特征）之间的相关系数。

7.3 散点图

散点图是一种可视化两个测量数据变量间关系的标准方法。在散点图中，x轴表示一个变量，y轴表示另一个变量，图中的每个点对应于一条记录。

plt.scatter(wine.Alcohol,wine.Proline)

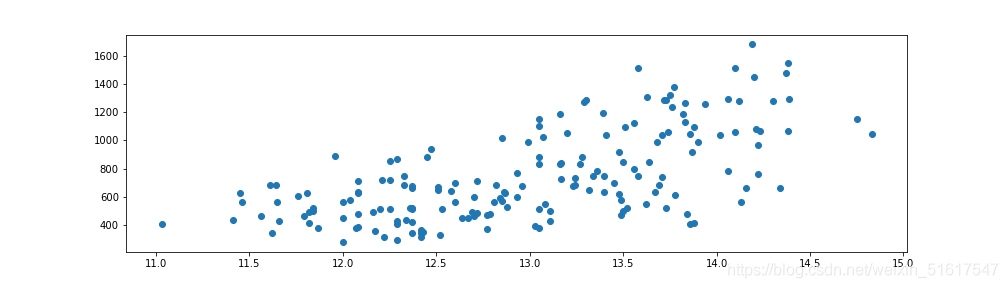
再以wine数据集中Alcohol与Proline两列为例绘出散点图。

8.探索多个变量

对一个变量进行分析称为单变量分析；对两个变量及其关系进行分析称为双变量分析，例如（线性）相关性分析；而对两个以上的变量进行分析称为多变量分析。与单变量分析一样，双变量分析不仅计算汇总统计量，而且生成可视化的展示。双变量或多变量分析的适用类型取决于数据本身，即数据是数值型数据还是分类数据。

8.1 双变量分析的可视化

多个变量的分析与可视化完全可以由双变量分析加上条件(conditioning)这个概念扩展得到，所以首先介绍几种关于两种变量的可视化方法，它们有六边形图、等势线、热力图、箱形图、小提琴图等。事实上，这些可视化方法本质上对应的都是直方图和密度图。

8.1.1 六边形图、等势线和热力图

六边形图、等势线和热力图均适用于两个数值型变量，它们所给出的都是二维密度的可视化表示。现再以wine数据集为例使用python实现可视化，简单地展示三种图像。

plt.hexbin(wine.Alcohol,wine.Proline,gridsize=30,cmap='Blues')
plt.colorbar()

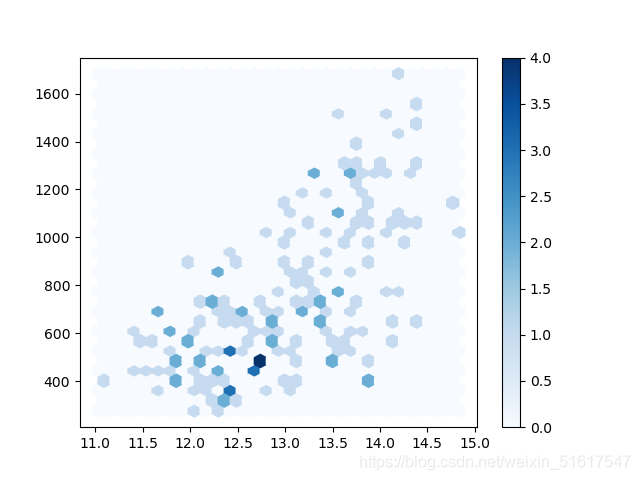
六边形图绘制的并非数据点，而是将记录（样本）分组为六边形的组距，并用不同的颜色绘制各个六边形，以显示每组中的记录数。

wine_AP=wine.loc[:,['Alcohol','Proline']]
sns.kdeplot(wine_AP)
plt.scatter(wine['Alcohol'],wine['Proline'])

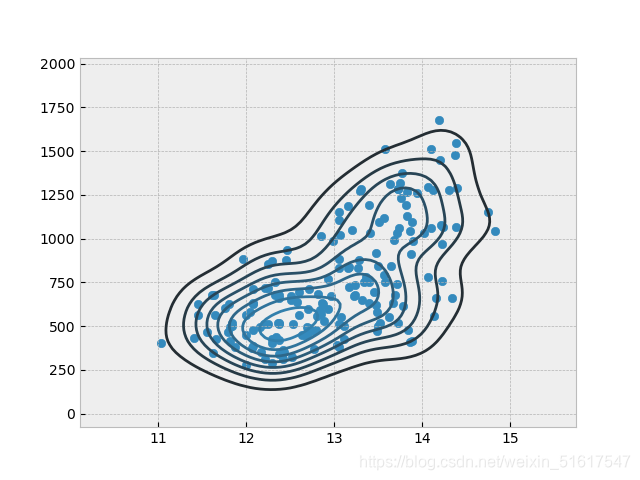
上图在散点图上绘制了一个等势线图（二维密度图），可视化了两个数值型变量之间的关系，等势线在本质上就是两个变量的地形图，每条等势线表示特定的密度值，并随着接近“顶峰”而增大。

wine_AP.set_index('Alcohol',inplace=True)
wine_AP_part=wine_AP.iloc[0:10]
sns.heatmap(wine_AP_part)

当然，一种可视化方法可以有多种用途，例如热力图还可以展现两个离散变量之间的组合关系或进行分类变量中数值型数据的相关性分析等。

8.1.2 箱形图和小提琴图

一些数值型数据是根据分类变量进行分组的，或者要同时比较多个变量的分布，可视化这类数据通常使用箱形图或小提琴图。

wine_BV=wine.loc[:,['Malic acid','Total phenols','Flavanoids','Proanthocyanins','Hue']]
sns.boxplot(data=wine_BV)

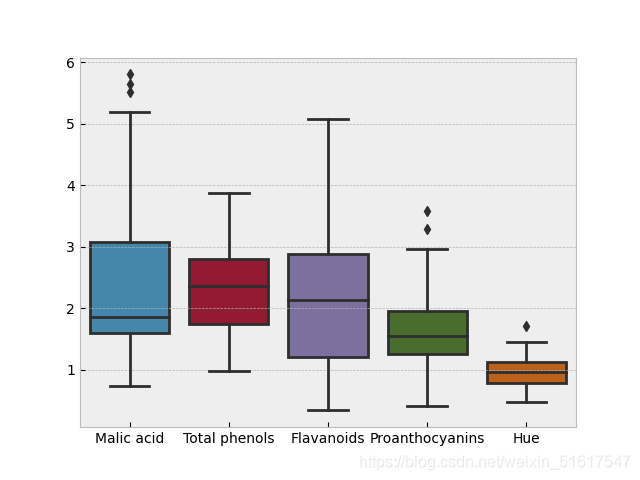
箱形图可以很直观的比较不同类别的（或不同特征的）数据分布。

sns.violinplot(data=wine_BV)

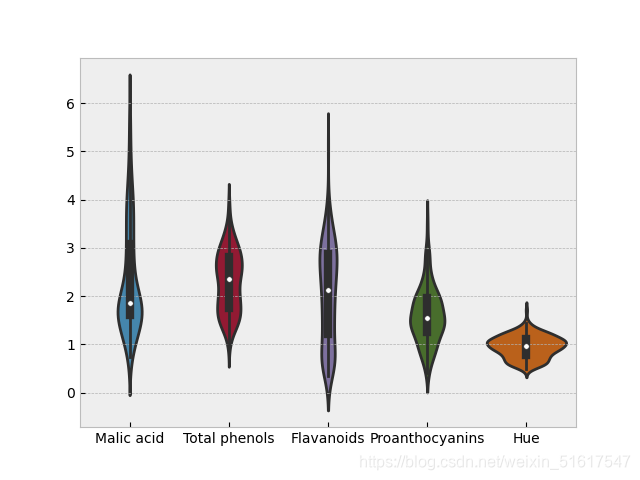
小提琴图是箱形图的一种增强表示，它以y轴为密度来绘制密度估计量的情况。绘图中对密度做镜像并反转（即核密度函数），并填充所生成的形状，由此生成了一个类似小提琴的图形。

sns.violinplot(data=wine_box,inner='quartile')

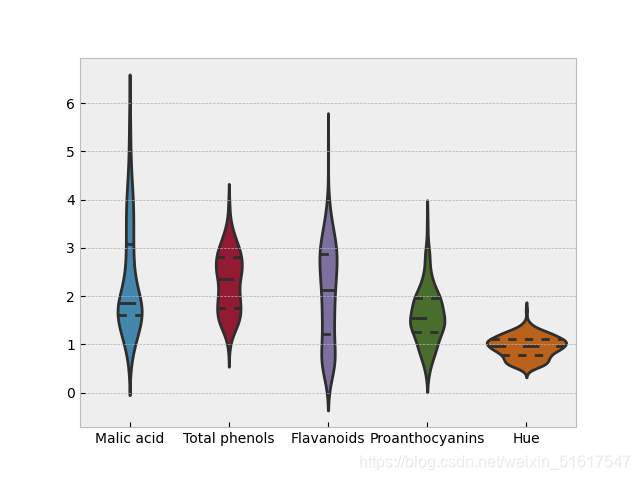
如果规定inner=‘quartile’，那么绘出的小提琴图相当图结合了箱形图，在某些情况下会有更好的效果。

8.2 多个变量的可视化

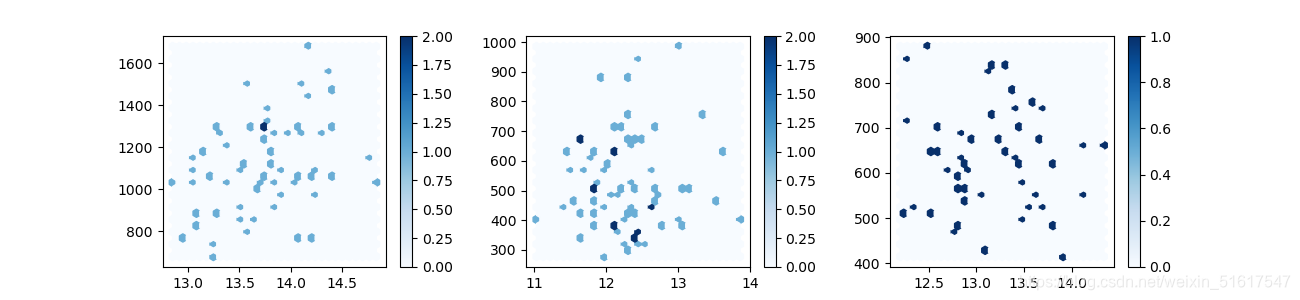
例如可视化上述数据集wine_AP（取特征Alcohol,Proline）时加入条件分别可视化不同等级（wine中的特征class,class=1,2,3）的数据，这就变成了一个多变量分析的可视化问题，我们通过建立多个子图来对比它们。例如：

wine_class1=wine.loc[wine['class']==1]
wine_class2=wine.loc[wine['class']==2]
wine_class3=wine.loc[wine['class']==3]
plt.figure()
plt.subplots_adjust(wspace=0.3)
plt.subplot(1,3,1)
plt.hexbin(wine_class1.Alcohol,wine_class1.Proline,gridsize=30,cmap='Blues')
plt.colorbar()
plt.subplot(1,3,2)
plt.hexbin(wine_class2.Alcohol,wine_class2.Proline,gridsize=30,cmap='Blues')
plt.colorbar()
plt.subplot(1,3,3)
plt.hexbin(wine_class3.Alcohol,wine_class3.Proline,gridsize=30,cmap='Blues')
plt.colorbar()
plt.rcParams['figure.figsize']=(13,3)

后记

到这里，对于探索性数据分析的简要介绍就结束了。对于任意基于数据的项目，最重要的第一步都是查看数据，这正是探索性数据分析的关键理念所在。通过总结并可视化数据，我们可以对项目获得有价值的洞悉和理解。从位置估计和变异性估计等简单度量，到探索多个变量之间的关系，我们可以借助各种技术和工具并结合python这样的语言强大的表达能力来建立丰富多样的数据探索和分析方式。

在最后，希望本文能够帮助到阅读的各位，也请大家多多关注，笔者会在后续介绍更多有关数据科学的内容以及使用python等语言进行数据分析的方法。