A题 疫苗生产问题
正太分布公式
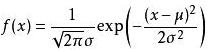
第一问是从50次时间统计出均值、方差作为正太分布的参数,最值即是公式中的x区间范围。
第一问的统计主要是得到不同疫苗在不同工序上的随机时间的正太分布公式
Matlab自带normrnd有部分问题,可以参考下下面我写的自定义函数
function [a,b]=nor(u,o,m1,m2)%u为均值,o为标准差,m1为区间最小值,m2为区间最大值b=rand;while b>1/(sqrt(2*pi)*o)b=rand;endif rand>0.5a=u+sqrt(-2*o*o*log(b*sqrt(2*pi)*o));elsea=u-sqrt(-2*o*o*log(b*sqrt(2*pi)*o));endif a<m1a=m1;endif a>m2a=m2;end
每种疫苗必须按照CJ1-CJ2-CJ3-CJ4依次加工,题目没有说几条生产线,那么就默认1条,第二问YM1-YM10各100剂已知,疫苗生产也不允许插队,就是说之后的工位也是按第一个工位的加工顺序加工疫苗。那么第二问就直接通过randperm函数生成随机序列就好。加工过程主要有两种增大时间成本的情况:第一种是YM2在CJ1加工完成后YM1还在CJ2上加工,第二种是YM1在CJ2加工完成后,YM2还在CJ1上加工。
造成了等待时间和空挡时间,因此就需要找到一个最优的加工排序方法,在第二问每种疫苗在不同工位的加工时间以附件1中平均时间为依据。加工时间案例程序如下:
T=zeros(1,4);for j=1:10T(1)=T(1)+A(chrom(i,j),1);%CJ1时间直接累加就行for k=2:4if T(k)<T(k-1)%YM2在CJ1加工完成后YM1还在CJ2上加工这种情况程序中不用体现延迟时间%第二种是YM1在CJ2加工完成后YM2还在CJ1上加工程序中需要体现延迟时间T(k)=T(k-1);endT(k)=T(k)+A(chrom(i,j),k);endend
程序设计很简单,每个个体就是randperm生成的序列,目标函数为总加工时间,优化算法就套用遗传算法就行,但交叉变异函数需要重新写下,下面是交叉变异函数案例,可以参考。
function x=jiaocha(x,n,a)if nargin < 3a=0.3;%未设置交叉率则默认为0.3endy=x(end:-1:1);b=randi(n); %生成随机交叉点if rand<ax=[x(b:end),x(1:b-1)];endfunction selchrom=bianyi(selchrom,n,a)if nargin < 3a=0.7;%未设置变异率则默认为0.7endfor i=1:length(selchrom)if rand<ab=randi(n);d=selchrom(i);c=find(selchrom==b);selchrom(i)=b;selchrom(c)=d;endEnd
第三问,时间改为满足正态分布的随机时间,但是要注意不同疫苗在不同工位加工时间的正态分布公式,其时间的区间范围由附件1中的最值决定的,随机产生时间请参阅前文自定义函数。加工时间案例如下
T=zeros(1,4);i=1;for j=1:10B(j,1)=chrom(i,j);B(j,2)=T(1);[a,b]=nor(A(chrom(i,j),1),2*S(chrom(i,j),1),Mi(chrom(i,j),1),Mx(chrom(i,j),1));D1(j,1)=a;D2(j,1)=b;T(1)=T(1)+a;%CJ1时间直接累加就行for k=2:4if T(k)<T(k-1)%YM2在CJ1加工完成后YM1还在CJ2上加工这种情况程序中不用体现延迟时间%第二种是YM1在CJ2加工完成后YM2还在CJ1上加工程序中需要体现延迟时间T(k)=T(k-1);end[a,b]=nor(A(chrom(i,j),k),2*S(chrom(i,j),k),Mi(chrom(i,j),1),Mx(chrom(i,j),1));D1(j,k)=a;D2(j,k)=b;T(k)=T(k)+a;endB(j,3)=T(end);end
本问的程序架构与第二问一致,只不过将第二问遗传算法作为外循环,对内某个个体循环进行k次蒙塔卡罗实验模拟,根据k次随机加工时间下的结果去评判这些个体的优劣,实验结束保留最优情况。
同时将模拟实验存在时间缩短5%以上个体作为优先排序条件,排序函数可以用sortrows函数实现多个从大到小或者从小到大优先级排序。
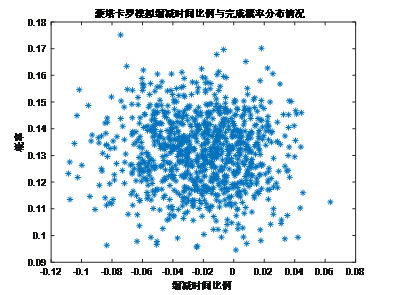
第三问还说找缩短的时间比例和最大概率之间的关系,先寻优出最优个体,然后基于该个体进行K次蒙特卡罗模拟实验,可以得到不同缩减比每次实验的分布情况,统计概率后可以通过最小二乘非线性拟合得到关系曲线和关系式。

第四问,每种类型疫苗的生产任务不可以拆分,相当于一种疫苗不间断生产,那么还是按randperm对10种不同疫苗产生随机序列用优化算法寻优,这里也需要注意下,每种疫苗其实是分成若干个100剂的且是连续加工的,全部加工完了一种疫苗后才换下一个序号的疫苗,同样采用第三问程序来做。
第五问,可以对任务进行拆分,将任务拆分并编号,同时记录疫苗种类,可以通过randperm产生随机序列,程序中将算目标函数的for循环改为while循环,终止条件为>100天,目标函数改为销售额。
B题 消防救援问题
第一问首先从附件中筛选出每年2月、5月、8月、11月中第一天三个时间段救援次数,基数是三个时间段至少5人,其他的按历史救援次数比例安排值班人员,当然这里也可以假设一次出警人数,一次出警时间,按时间点统计下历史数据中该时间段需求最多的人数,也可以结合区域的人口密度,设置不同的出警人数,可以假设的方面很多。第一问也只是说每年2月、5月、8月、11月中第一天的三个时间段各应安排多少人值班,根据历史数据统计就行,不需要进行预测。
第二问可以直接用神经网络、时间序列的方法来做,或者拆成每日用马尔可夫预测最后在按月求和。最后做下误差分析。数据不是很有规律,多尝试几种预测方法。
第三问,观察发现数据基本无规律性,比较像随机事件,本问比较科学的做法是预测次数和预测事件发生分开来做,按月的角度去预测之后每月救援的次数,预测时间的发生就不按时间点来了,直接通过马尔可夫算法(其中有转移概率矩阵,比较适合解本问)预测后续时间发生的序列,最后得到每月不同时间发生的次数。
第四问,先计算各地区2016-2020年不同事件的密度(按每周统计[事件密度指每周每平方公里内的事件发生次数]),根据图1,求与连接区域不同事件密度数据的相关性,比如拿A区事件1与B区事件1求其密度历史每周数据的相关性(皮尔逊、余弦相似度等),给出两个连接区域间相关性最强的事件是哪一类。题目说图1中空间上的相关性,应该指的是相连通的区域。
第五问,本问的各类事件密度就取每周的平均值,然后分每一类事件求其时间密度与对应区域人口密度的关系,这里就可以用简单的回归分析算法,主要是体现整体趋势。
第六问,如果是要依次新建消防站,就仅考虑当前情况,FCM算法(可以参考下我公众号的推文:算法-Matlab版-FCM聚类)以点到相应聚类中心距离之和最短为目的,本问可以借鉴该思路,除了距离外,还可以考虑平均每年出警的次数以及人口密度等因素,去构建目标函数。本问区域个数较小,可以直接枚举出来确定最优选址,每新建一个消防站重新算一下新增消防站的最佳位置即可。
C题 数据驱动的异常检测与预警问题
数据有些不连续波动且波动值很小可能是传感器短时间发生异常,这类波动视为非风险性异常,如果是连续波动且偏移量较大,并且可能还对其他传感器有一定的联动性,那么基本上可以判定为风险性异常,给大家解释下几个方面,部分传感器接收到的信号来源是一致的,也就是题目说道的联动性,由于没有历史数据支撑,也不知道各传感器的状态,可以取初始前几十行数据通过求相关性、聚类分析进行归类,归一下类别,之后如果出现异常数据联动的时候可以多一个参考,聚类步骤可有可无。还有一点,传感器一天内受天气的影响肯定很多传感器在早中晚时的数据差异比较明显,因此最好不要直接用算法检测整列数据。比较科学的做法,我们拿半小时为例,大概有120个数据。程序里每次循环向下增加一行,向上减少一行,一个时刻一个时刻的遍历下去,对于单个传感器,可以通过LOF离群度检测算法(可以参考下我公众号的推文:算法-Matlab版-LOF)
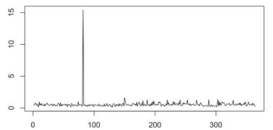
每新增一个数据就重新算一次离群度值,离群度这里可以设个临界值,高于则视为异常数据,按理说如果是正常数据都是连续的,那么离群度就不会太高,如果是出现连续几个偏差较大的数据那么就可以判断疑似风险性异常,同时可以根据与之同类的传感器数据的异常情况,如果存在异常联动那么就判定为该时刻发生风险性异常,如果不存在异常联动,就继续遍历,如果连续又增加了几个高离群度的值,那么就可以判定为风险异常。异常检测肯定是有延迟的,聚类步骤也只是辅助LOF算法尽早发现风险异常,还有种情况,数据异常时间比较长,这里可以记录下确认风险性异常前120个数据的平均值u和方差o,此时新增的数据的离群度就暂时以u和o来计算。此刻被定义为风险异常,可能在之后某一时刻工作人员恢复了数据,如何判断恢复时刻,如果出现连续几个数据小于与u<方差o那么可以视为恢复,考虑天气、时间变化的影响,这里也可以加一个容错系数p,那么就是<方差o+p视为恢复。从恢复时刻开始,前面的数据就可以摒弃了,就从恢复时刻开始一直到120个数据后再依次取下一120个数,依次遍历下去。特别提醒下不管用什么异常检测算法一定要增加恢复时刻的判断,否则遍历到后面可能会将已恢复后的数据也判断为风险性异常。
上述主要从算法设计角度写的,可以参考下,也可以更细化多增加一些判定条件,实现起来编程也确实要麻烦点。
第二问,第一问采用的是遍历采样的方式,每个传感器每个时刻都会取前120个数据,第一问也设立了恢复时刻的判定,这里百分制打分就按离群度值/历史出现最高离群度值,如果存在联动异常则打分×(1+theta)。打分模型可以自己根据第一问的算法构建,这里只是举了个简单的例子。
第三问,预测算法推荐使用粒子滤波算法(可以参考下我公众号的推文:算法-Matlab版-粒子滤波),预测算法带入的数据最好是22:00-23:00的,时间久的数据参考意义不大。然后再接着第二问算下23:00-0:00的各时间点评分
第四问,注意这里是安全性评分了,并且是对时间段所有传感器的整体情况进行评分,一般我们在企业里会有故障这一指标,在本问评分可以通过这个式子计算100*(1-故障总时长/所有设备开机时长)或者100*(1-故障设备数/该时段总设备工作数)