专栏导读
作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元类型包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3.物理场问题涉及:力学、传热学、电磁学及多物理场耦合等问题的稳态(静力学)和瞬态(动力学)求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴,快速上手有限元编程,在案例中成长,摆脱按部就班填鸭式教学。【所有专栏文章均提供视频教程和源码】《有限元编程从入门到精通30讲》视频教程与源码获取地址: https://www.bilibili.com/video/BV1kP4y1d7Zo欢迎订阅专栏,订阅用户可私聊进入有限元编程交流群(知识交流、问题解答),并获赠丰厚的有限元相关学习资料(教材、源码、视频课)专栏订阅地址:有限元编程从入门到精通_suoge223的博客-CSDN博客导读
本文主要讲解如何利用Matlab通过有限元编程实现框架结构在地震作用下弹性时程分析,重点介绍了Newmark-Beta求解方法(隐式方法)和瑞丽阻尼矩阵的基本原理及算法流程,并通过Matlab程序介绍了Newmark-Beta方法的和瑞丽阻尼矩阵的程序实现过程,其中框架结构采用铁木辛柯梁单元,其有限元方程的建立过程可参考往期博文《Matlab梁单元有限元编程:铁木辛柯梁VS欧拉梁讲解》。最终程序求解得到框架结构整体的位移时程,并通过震动动画进行展示,如下图所示。
【本案例 源码】 获取:https://mbd.pub/o/bread/mbd-ZZ2UlJxq
【本案例 视频+源码+课件】 获取:https://www.fangzhenxiu.com/course/5647124/
【有限元合集课】【视频+源码+课件】 获取:https://www.fangzhenxiu.com/course/5190666/
框架结构地震作用下的动画
一、时间积分的隐式与显式方法
时间积分法瞬态求解器用于求解各类满足下述方程的瞬态物理问题:
![]()
如结构动力学问题等,其求解过程与时间相关,求解结果为物理量随时间变化的历程。其中,M、C、K为对应物理问题系数矩阵,如结构动力学问题的结构质量矩阵、阻尼矩阵和刚度矩阵; u,u˙,u¨ 为对应物理问如结构动力学问题的结构位移、速度和加速度;f为对应物理问题的外部作用,如结构动力学问题的外部动力荷载。在时间积分技术中,当前时间步的未知值是基于前一个时间步的已知值计算得出的。根据计算过程和应用,时间积分技术可以分为两种类型:隐式和显式。让我们通过以下显示的位移(u)和速度(u')方程,在时间步(tn+1)上讨论这两种技术之间的差异。 在隐式时间积分方法中,未知时间步的变量是通过使用未知时间步(tn+1)处的斜率(u',u'')来计算的。由于位移、速度和加速度在时间步(tn+1)上是未知的,因此不能直接求解这些方程。比较典型的隐式时间积分法是Newmark-beta法,将在后文重点介绍。
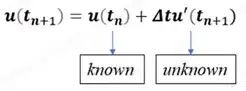
在显式方法中,我们使用已知时间步的斜率(u',u'')来计算未知时间步(tn+1)处的变量。由于位移、速度和加速度在时间步(tn)上是已知的,因此可以直接求解这些方程。中心差分法是典型的显示求解算法,在求解瞬t+dt时的位移U时,只需t+dt时刻以前的状态变量Ut,和U(t-dt),然后计算出有效质量矩阵,有效载荷矢量,即可求出U(t+dt),故称此解法为显式算法。时间步长的选择直接关系到数值算法的稳定性和计算时间。中心差分法的实质是用差分代替微分,并且对位移和加速度采用线性外插,这就限制了步长不可能过大,否则结果可能失真,显式方法可参考博文《Matlab中心差分法求解单自由度系统受迫振动》。本文重点介绍newmark-beta隐式方法

对于线性问题,上述两种方法从计算效率上没有明显的差别,但是对于非线性问题,隐式算法涉及迭代求解会影响计算效率。
二、Newmark-Beta求解方法(隐式)
有限元计算分析软件的时间积分法瞬态求解器采用 作为求解方法。本文以结构动力时程分析问题为例,对 法进行介绍。 结构动力时程问题的基本方程如下:
![]()
其中,M、C、K分别是结构的质量、阻尼和刚度矩阵;u(t),u_dot(t),u_ddot(t)分别是结构任意时刻的位移、速度和加速度响应;f(t)是结构受到的随时间变化的外部激励。为求得各时间点的结构响应, 法对结构响应作如下假定:

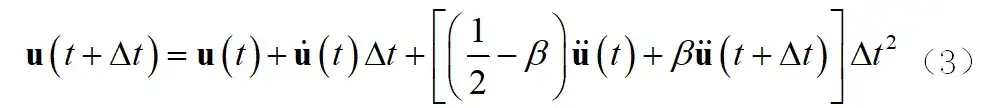
其中, 和 是根据所需积分精度和稳定性来确定的参数, 为积分时间步长。 由式(3)得到:
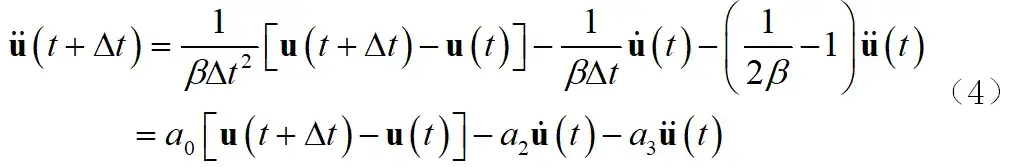
将式(4)代入式(2)并整理得到:

将式(3)、(4)、(5)代入时刻的方程(1)并整理得到:

将式(6)整理后得到:
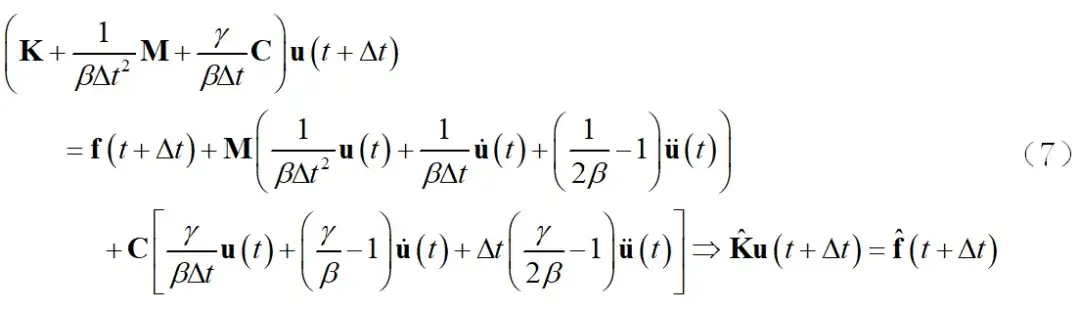
其中:
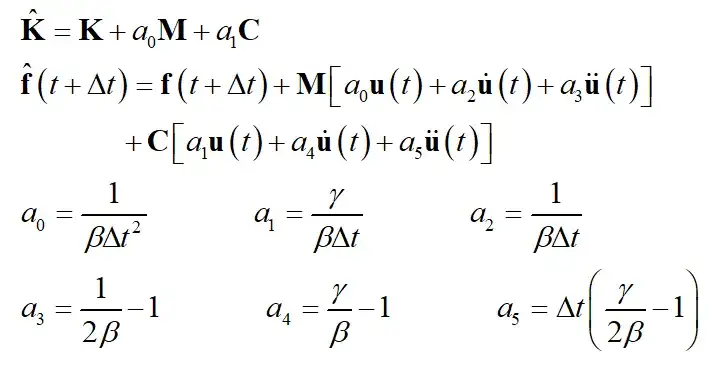
由式(4)、(2)得到:

其中:
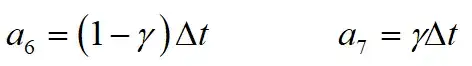
通过上述推导可知,对于一个结构,只要确定了结构的初始状态(t=0时刻的结构响应)和外部激励,就可以通过公式(7)、(8)和(9),利用t时刻的结构响应,将结构 时刻的动力方程转化为一个等效的静力平衡方程(7),从而计算得到 时刻结构的各个响应,进而逐步积分得到整个结构的动力响应。对每一时刻等效静力平衡方程(7)的求解,可直接采用静力学求解器进行求解,本质依然是求刚度矩阵的逆矩阵。
三、阻尼矩阵的建立
本文时程分析采用Rayleigh阻尼阵形式(瑞利阻尼矩阵)即
![]()
其中[M]和[K]分别是系统的质量矩阵和刚度矩阵;a0为与质量成比例的系数;a1为与刚度成比例的系数。 在瑞丽阻尼系统中,第i阶振型的阻尼比为

若定义第i,j阶振型的阻尼比,并列上式可以得到:
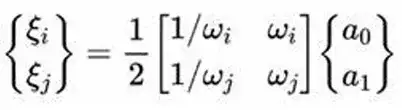
反解可以得到a0,a1的表达式
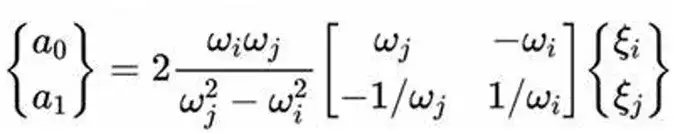
因此在程序中定义瑞丽阻尼矩阵时需要对系统进行模态分析,得到响应各阶模态的频率。带入上式进行a0,a1的计算,进而得到阻尼矩阵。
四、Newmark-Beta程序算法及源码
基于上一节的计算原理可以提炼出编程所需的算法流程,具体如下所示。

与上述newmark-beta算法对应的Matlab代码如下:
function[uu,vv,aa,ttt]=NewmarkBeta1(t,dt,delta,beta,M,C,K,acc_x,Constr)n=length(t);beta=0.25;gamma=0.5;a0=1/(beta*dt^2);a1=gamma/(beta*dt);a2=1/(beta*dt);a3=1/(2*beta)-1;a4=gamma/beta-1;a5=(dt/2)*(gamma/beta-2);a6=dt*(1-gamma);a7=dt*gamma;uu(:,1)=zeros(size(M,1),1);;%位移初始值vv(:,1)=zeros(size(M,1),1);%速度初始值aa(:,1)=zeros(size(M,1),1);%加速度初始值P(:,1)=zeros(size(M,1),1);%荷载初始值P1(:,1)=zeros(size(M,1),1);%等效荷载初始值%I=ones(size(M,1),1);;%6*1单位阵I=zeros(size(M,1),1);;%6*1单位列向量fori=1:size(K,1)/3I(3*(i-1)+1)=1;%确定惯性力施加的自由度endK1=K+a0*M+a1*C;%形成等效刚度矩阵fori=1:n-1P(:,i+1)=-M*I*acc_x(i+1);%t(i+1)时刻结构的荷载P1(:,i+1)=P(:,i+1)+M*(a0*uu(:,i)+a2*vv(:,i)+a3*aa(:,i))+C*(a1*uu(:,i)+a4*vv(:,i)+a5*aa(:,i));%t(i+1)时刻结构的等效荷载uu(:,i+1)=(K1)\P1(:,i+1);%t(i+1)时刻结构的位移aa(:,i+1)=a0*(uu(:,i+1)-uu(:,i))-a2*vv(:,i)-a3*aa(:,i);%t(i+1)时刻结构的加速度vv(:,i+1)=vv(:,i)+a6*aa(:,i)+a7*aa(:,i+1);%t(i+1)时刻结构的速度ttt(i+1)=dt*(i-1);end