PID 控制（比例-积分-微分控制，Proportional-Integral-Derivative Control）是一种广泛使用的反馈控制策略，用于自动控制系统中。PID 控制器通过调整系统的控制输入，以使系统的输出能够稳定在目标值上。
一、PID 控制器的工作原理
PID 控制器基于三个基本的控制机制：
1.1 比例控制（Proportional Control, P）：
功能：通过比例控制项，控制器输出与偏差（目标值与当前值之间的差）成正比。
作用：增加比例增益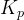
可以提高系统响应速度，但过高的比例增益可能导致系统震荡或不稳定。
1.2 积分控制（Integral Control, I）：
功能：通过积分控制项，累计过去的偏差，消除稳态误差。
作用：积分增益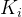
可以消除系统的长期稳态误差，但过高的积分增益可能引起系统超调或振荡。
1.3 微分控制（Derivative Control, D）：
功能：通过微分控制项，预测偏差的未来趋势，增加系统的稳定性和响应速度。
作用：微分增益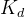
可以改善系统的瞬态响应，减少过冲和振荡，但对噪声较为敏感。
二、PID 控制器的综合公式
PID 控制器的输出是比例、积分和微分控制的组合：
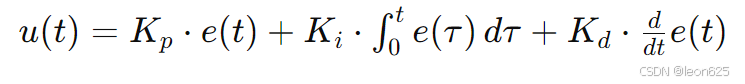
其中：
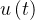是控制器的输出。
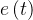是当前时刻的偏差（目标值与实际值之间的差）。
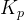是比例增益。
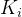是积分增益。
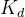是微分增益。 三、PID 控制器的调节
PID 控制器的性能很大程度上取决于比例、积分和微分增益的设置。常见的调节方法包括：
手动调节：逐步调整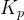
,
,
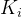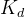的值，观察系统响应，并根据实际情况进行调整。Ziegler-Nichols 方法：通过系统的临界增益和临界振荡周期来确定 PID 参数。自动调节：使用算法和软件工具自动计算 PID 参数，以优化系统性能。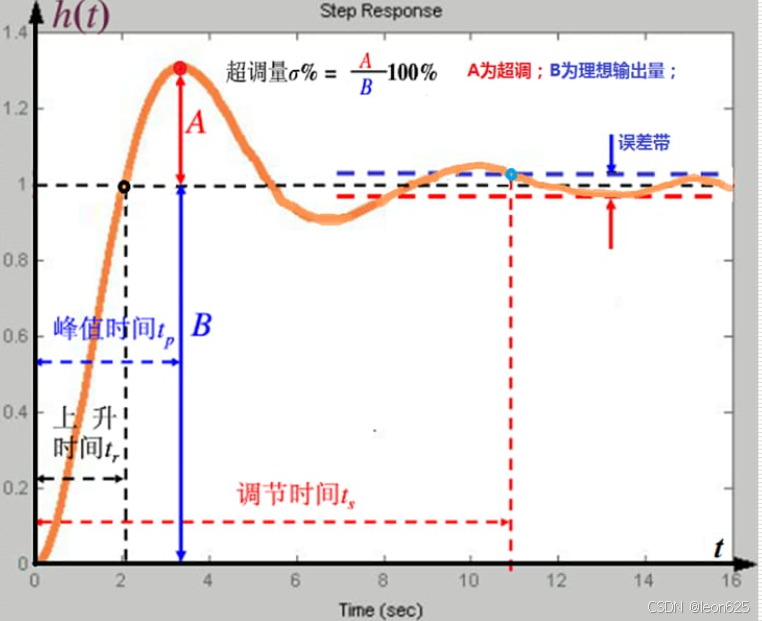 
四、PID 控制器的优缺点
4.1 优点：
简单性：PID 控制器设计简单，易于理解和实现。适用范围广：适用于各种线性和非线性系统的控制。实时控制：能够快速响应系统的变化，实现实时控制。4.2 缺点：
调节复杂性：PID 参数的调节可能需要经验和时间，尤其是在复杂系统中。对噪声敏感：微分项对噪声敏感，可能需要进行噪声滤波。不能处理系统建模错误：PID 控制器对系统模型的变化不敏感，可能在系统特性变化时表现不佳。五、应用领域
PID 控制器被广泛应用于各个领域，包括：
工业自动化：用于控制温度、压力、流量等。机器人控制：用于机器人运动控制、路径跟踪等。航天工程：用于飞行器姿态控制、轨迹跟踪等。家电产品：用于温控、速度控制等。六、MATLAB仿真程序
% PID控制器MATLAB仿真程序% 系统参数a = 0.1; % 系统的时间常数b = 1; % 系统增益dt = 0.01; % 仿真时间步长T = 10; % 仿真总时间time = 0:dt:T; % 时间向量% PID参数初始化Kp = 1; % 比例增益Ki = 0.1; % 积分增益Kd = 0.01; % 微分增益% 初始化变量y = zeros(size(time)); % 系统输出e = zeros(size(time)); % 误差u = zeros(size(time)); % 控制输入error_integral = 0; % 积分项prev_error = 0; % 上一个误差% 设定点setpoint = 1;% 仿真for i = 2:length(time) % 计算误差 e(i) = setpoint - y(i-1); % PID控制器计算 error_integral = error_integral + e(i) * dt; error_derivative = (e(i) - prev_error) / dt; % 控制输入 u(i) = Kp * e(i) + Ki * error_integral + Kd * error_derivative; % 系统更新（Euler方法） y(i) = y(i-1) + dt * (-a * y(i-1) + b * u(i)); % 更新误差 prev_error = e(i);end% 绘制结果figure;subplot(3,1,1);plot(time, y, 'b', time, setpoint*ones(size(time)), 'r--');title('System Output');xlabel('Time (s)');ylabel('Output');legend('Output', 'Setpoint');subplot(3,1,2);plot(time, e, 'g');title('Error');xlabel('Time (s)');ylabel('Error');subplot(3,1,3);plot(time, u, 'k');title('Control Input');xlabel('Time (s)');ylabel('Control Input');七、总结
PID 控制器是一种经典且有效的控制策略，通过比例、积分和微分三部分的调节，能够提供稳定的控制输出。虽然其设计和调节相对简单，但在实际应用中需要根据系统的具体需求进行调整，以实现最佳性能。