引言
GLM扩展了传统的线性回归模型,使其能够处理更复杂的数据类型和分布
文章目录
引言一、广义线性模型1.1 定义1.2 广义线性模型的组成1.2.1 响应变量(Response Variable)1.2.2 链接函数(Link Function)1.2.3 线性预测器(Linear Predictor) 1.3 常见的广义线性模型1.3.1 线性回归1.3.2 逻辑回归1.3.3 泊松回归 1.4 GLM的特性1.5 广义线性模型的拟合1.6 应用场景1.7 优点1.7.1 灵活性1.7.2 广泛的分布选择1.7.3 链接函数的多样性1.7.4 非恒定方差的适应性1.7.5 易于理解和解释1.7.6 统计推断的可用性1.7.7 软件支持 1.8 缺点1.8.1 假设的严格性1.8.2 对异常值敏感1.8.3 计算复杂性1.8.4 过度拟合的风险1.8.5 难以处理高维数据1.8.6 不适用于某些复杂关系1.8.7 模型选择的挑战 1.9 总结 二、广义线性模型在python中的实例2.1 实现GLM的基本步骤2.1.1 使用 `statsmodels` 实现 GLM2.1.1.1安装 `statsmodels`2.1.1.2 使用 `statsmodels` 实现逻辑回归(Logistic Regression) 2.1.2 使用 `scikit-learn` 实现 GLM2.1.2.1 安装 `scikit-learn`2.1.2.2 使用 `scikit-learn` 实现逻辑回归
一、广义线性模型
1.1 定义
广义线性模型(Generalized Linear Models,简称GLM)是一种用于描述响应变量与一组解释变量之间关系的高级统计模型
1.2 广义线性模型的组成
1.2.1 响应变量(Response Variable)
在GLM中,响应变量可以是连续的或离散的,并且可以遵循不同的概率分布。这与传统线性模型中响应变量必须是连续且正态分布的限制不同
1.2.2 链接函数(Link Function)
链接函数是GLM的核心组成部分,它建立了线性预测器(解释变量的线性组合)和响应变量的期望值之间的联系。链接函数的选择取决于响应变量的分布类型
1.2.3 线性预测器(Linear Predictor)
线性预测器是解释变量的线性组合,通常表示为 η = X β \eta = X\beta η=Xβ,其中 X X X是设计矩阵, β \beta β是参数向量
1.3 常见的广义线性模型
1.3.1 线性回归
当响应变量是连续的且遵循正态分布时,GLM退化为传统的线性回归模型,此时链接函数是恒等函数
1.3.2 逻辑回归
当响应变量是二进制的(0-1变量)时,通常使用逻辑回归。在这种情况下,响应变量遵循二项分布,链接函数通常是logit函数
1.3.3 泊松回归
当响应变量是计数数据时,泊松回归是适用的。响应变量遵循泊松分布,链接函数通常是自然对数函数
1.4 GLM的特性
灵活性:GLM可以处理各种类型的响应变量,包括连续、二元、计数和多分类数据非恒定方差:GLM允许响应变量的方差依赖于其均值,这是通过方差函数(Variance Function)来实现的非线性:通过选择适当的链接函数,GLM可以模拟非线性关系1.5 广义线性模型的拟合
GLM的拟合通常涉及以下步骤:
选择合适的概率分布和链接函数来描述响应变量使用最大似然估计(Maximum Likelihood Estimation,MLE)或其他优化方法来估计模型参数进行模型诊断和假设检验,以确保模型的有效性和可靠性1.6 应用场景
GLM在多个领域都有广泛的应用,包括:
生物统计学和流行病学金融和经济学社会科学和市场营销生态学和环境科学1.7 优点
1.7.1 灵活性
GLM可以处理多种类型的响应变量,包括连续、二元、计数和多分类数据,适应不同的数据结构和分布
1.7.2 广泛的分布选择
通过选择不同的概率分布,GLM能够适应不同的数据类型和分布特性,如正态分布、二项分布、泊松分布等
1.7.3 链接函数的多样性
GLM允许使用不同的链接函数,这使得模型可以模拟复杂的非线性关系
1.7.4 非恒定方差的适应性
GLM可以处理响应变量的方差随着均值变化的情况,这在许多实际问题中很常见
1.7.5 易于理解和解释
GLM保留了线性模型的许多解释性,如参数的线性组合,使得模型结果易于理解和交流
1.7.6 统计推断的可用性
GLM提供了参数估计、假设检验和置信区间等统计推断工具,有助于模型的验证和解释
1.7.7 软件支持
大多数统计软件和编程语言都提供了GLM的实现,如R、Python、SAS、SPSS等,便于用户使用
1.8 缺点
1.8.1 假设的严格性
GLM依赖于一系列假设,如响应变量的分布、链接函数的正确选择、方差函数的形式等。如果这些假设不满足,模型的准确性和可靠性会受到影响
1.8.2 对异常值敏感
GLM对异常值和离群点敏感,这些数据点可能会对模型参数估计产生较大影响
1.8.3 计算复杂性
对于某些复杂的模型,尤其是当数据量大或者模型参数多时,GLM的计算可能会变得复杂和耗时
1.8.4 过度拟合的风险
在模型选择过程中,如果包含过多的解释变量或者使用了过于复杂的链接函数,可能会导致过度拟合
1.8.5 难以处理高维数据
在处理高维数据(解释变量远多于观测值)时,GLM可能会遇到变量选择和模型解释的困难
1.8.6 不适用于某些复杂关系
GLM虽然比传统线性模型更灵活,但仍然无法捕捉某些非常复杂的数据关系,如非线性、非参数关系等
1.8.7 模型选择的挑战
选择合适的概率分布和链接函数需要领域知识和经验,对于初学者来说可能是一个挑战
1.9 总结
广义线性模型是一种强大的统计工具,适用于多种数据分析场景,但其有效性和可靠性取决于正确应用模型和满足其假设条件。通过广义线性模型,研究人员和数据分析专家能够更好地理解和预测复杂的数据关系,从而在各个领域做出更准确的决策和预测。
二、广义线性模型在python中的实例
在Python中,广义线性模型(GLM)可以通过多个库实现,其中最常用的是statsmodels和scikit-learn
2.1 实现GLM的基本步骤
2.1.1 使用 statsmodels 实现 GLM
statsmodels 是一个强大的Python库,提供了广泛的统计模型估计和测试功能
2.1.1.1安装 statsmodels
如果还没有安装statsmodels,可以使用以下命令安装:
pip install statsmodels2.1.1.2 使用 statsmodels 实现逻辑回归(Logistic Regression)
import statsmodels.api as smimport statsmodels.formula.api as smfimport pandas as pdimport numpy as np# 设置随机种子以获得可重复的结果np.random.seed(0)# 创建一个包含两个解释变量的数据集n_samples = 100x1 = np.random.normal(loc=0, scale=1, size=n_samples)x2 = np.random.normal(loc=0, scale=1, size=n_samples)# 基于解释变量生成一个二进制响应变量# 使用logistic函数模拟真实世界中响应变量的生成z = 1 + 2 * x1 + 3 * x2 + np.random.normal(loc=0, scale=1, size=n_samples)p = 1 / (1 + np.exp(-z))y = np.random.binomial(n=1, p=p)# 创建DataFramedata = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})# 显示数据集的前几行# print(data.head())# 我们有一个数据集data,其中包含一个二进制响应变量y和一个或多个解释变量x1, x2, ...# 使用公式接口glm_model = smf.glm('y ~ x1 + x2', data=data, family=sm.families.Binomial()).fit()# 打印模型摘要print(glm_model.summary())# 获取参数估计params = glm_model.params# 进行预测predictions = glm_model.predict(data[["x1", "x2"]])输出结果:

family=sm.families.Binomial()指定了响应变量遵循二项分布,这是逻辑回归的典型设置glm函数还允许指定其他分布,如Poisson(泊松分布)或Gaussian(正态分布) 2.1.2 使用 scikit-learn 实现 GLM
scikit-learn 是一个流行的Python机器学习库,它提供了许多预定义的模型和工具
2.1.2.1 安装 scikit-learn
如果还没有安装scikit-learn,可以使用以下命令安装:
pip install scikit-learn2.1.2.2 使用 scikit-learn 实现逻辑回归
以下是一个使用scikit-learn库实现逻辑回归的完整代码示例。这个例子将使用之前生成的数据集,其中包含两个特征和一个二进制目标变量。
from sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import accuracy_score, classification_reportimport pandas as pdimport numpy as npfrom sklearn.datasets import make_classification# 设置随机种子以获得可重复的结果np.random.seed(0)# 使用make_classification生成数据集X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2, random_state=0, n_clusters_per_class=1)# 将特征和目标变量转换为DataFramedata = pd.DataFrame(X, columns=['feature1', 'feature2'])data['target'] = y# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split( data[['feature1', 'feature2']], data['target'], test_size=0.2, random_state=0)# 创建逻辑回归模型log_reg = LogisticRegression()# 拟合模型log_reg.fit(X_train, y_train)# 进行预测y_pred = log_reg.predict(X_test)# 计算准确率accuracy = accuracy_score(y_test, y_pred)print(f'准确率: {accuracy:.2f}')# 输出分类报告print(classification_report(y_test, y_pred))# 输出模型参数print(f'截距: {log_reg.intercept_}')print(f'系数: {log_reg.coef_}')输出结果:
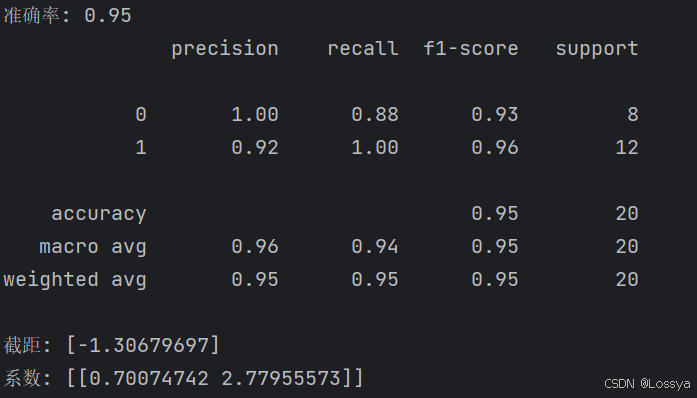
这段代码做了以下几件事情:
使用make_classification函数生成一个合成数据集将数据集划分为训练集和测试集创建一个LogisticRegression对象使用训练集数据拟合模型使用测试集数据评估模型的性能,包括准确率和分类报告打印出模型的截距和系数 请注意,这里使用了train_test_split函数来将数据集划分为训练集和测试集,比例为80%训练数据和20%测试数据
accuracy_score用于计算模型在测试集上的准确率,而classification_report提供了关于模型性能的更详细的报告,包括精确度、召回率和F1分数