一、遗传算法概述
1.1适用范围
遗传算法(Genetic Algorithm, GA)是一种启发式搜索算法,广泛应用于以下领域:
优化问题:如函数优化、路径规划、资源分配等。机器学习:用于特征选择、超参数优化等。经济与金融:如投资组合优化、期权定价等。工程设计:如电路设计、结构优化等。1.2步骤
遗传算法借鉴了自然界中生物进化的过程,主要包括以下几个步骤:
初始化:随机生成一组初始种群(解)。适应度评估:根据适应度函数评估每个个体的适应度。选择:根据适应度选择优秀的个体作为父代。交叉:通过交叉操作生成新的个体(子代)。变异:随机改变部分个体以增加种群多样性。替换:用子代替换父代,进入下一代迭代。1.3优点
适用性广:可以应用于各种复杂的优化问题。全局搜索能力强:不容易陷入局部最优。易于并行化:可以利用多处理器环境加速计算。1.4缺点
计算复杂度高:尤其是在种群规模和迭代次数较大的情况下。参数选择敏感:如交叉率、变异率等参数需要精心调整。收敛速度慢:在某些问题上可能需要较多代数才能找到满意的解。二、Python代码示例
2.1代码示例
以下是一个简单的遗传算法示例,用于解决函数优化问题:
import numpy as npimport random# 目标函数(待优化)def objective_function(x): return -x**2 + 4*x + 10# 初始化种群def initialize_population(size, bounds): population = [] for _ in range(size): individual = random.uniform(bounds[0], bounds[1]) population.append(individual) return population# 适应度评估def evaluate_population(population): return [objective_function(individual) for individual in population]# 选择(轮盘赌选择)def select(population, fitness): total_fitness = sum(fitness) probabilities = [f/total_fitness for f in fitness] selected = np.random.choice(population, size=len(population), p=probabilities) return selected# 交叉(单点交叉)def crossover(parent1, parent2): point = random.randint(1, len(parent1)-1) child1 = parent1[:point] + parent2[point:] child2 = parent2[:point] + parent1[point:] return child1, child2# 变异def mutate(individual, mutation_rate, bounds): if random.random() < mutation_rate: individual = random.uniform(bounds[0], bounds[1]) return individual# 遗传算法主函数def genetic_algorithm(objective_function, bounds, population_size, generations, mutation_rate): # 初始化种群 population = initialize_population(population_size, bounds) for generation in range(generations): # 评估种群适应度 fitness = evaluate_population(population) # 选择 selected_population = select(population, fitness) # 生成新种群 new_population = [] for i in range(0, len(selected_population), 2): parent1 = selected_population[i] parent2 = selected_population[i+1] child1, child2 = crossover(parent1, parent2) new_population.append(mutate(child1, mutation_rate, bounds)) new_population.append(mutate(child2, mutation_rate, bounds)) population = new_population # 返回最佳个体 best_individual = max(population, key=objective_function) return best_individual# 参数设置bounds = [0, 10]population_size = 20generations = 50mutation_rate = 0.1# 执行遗传算法best_solution = genetic_algorithm(objective_function, bounds, population_size, generations, mutation_rate)print(f"最佳解:{best_solution}, 目标函数值:{objective_function(best_solution)}")2.2代码解释
objective_function: 目标函数,用于评估个体的适应度。initialize_population: 初始化种群,生成一定范围内的随机个体。evaluate_population: 评估种群中每个个体的适应度。select: 轮盘赌选择,基于适应度概率选择个体。crossover: 单点交叉操作,生成子代个体。mutate: 变异操作,随机改变个体。genetic_algorithm: 遗传算法的主函数,执行初始化、选择、交叉、变异等操作。三、可运行案例:用Python实现遗传算法
3.1案例代码
为了演示遗传算法的运行结果,我们以优化一个简单的二次函数为例,假设我们要找到函数 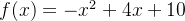 的最大值。以下是详细的代码和运行结果的分析:
的最大值。以下是详细的代码和运行结果的分析:
import numpy as npimport randomimport matplotlib.pyplot as plt# 目标函数(待优化)def objective_function(x): return -x**2 + 4*x + 10# 初始化种群def initialize_population(size, bounds): population = [] for _ in range(size): individual = random.uniform(bounds[0], bounds[1]) population.append(individual) return population# 适应度评估def evaluate_population(population): return [objective_function(individual) for individual in population]# 选择(轮盘赌选择)def select(population, fitness): min_fitness = min(fitness) if min_fitness < 0: fitness = [f - min_fitness for f in fitness] # 平移使所有适应度非负 total_fitness = sum(fitness) probabilities = [f/total_fitness for f in fitness] selected = np.random.choice(population, size=len(population), p=probabilities) return selected# 交叉(单点交叉)def crossover(parent1, parent2): child1 = (parent1 + parent2) / 2 child2 = (parent1 + parent2) / 2 return child1, child2# 变异def mutate(individual, mutation_rate, bounds): if random.random() < mutation_rate: individual = random.uniform(bounds[0], bounds[1]) return individual# 遗传算法主函数def genetic_algorithm(objective_function, bounds, population_size, generations, mutation_rate): # 初始化种群 population = initialize_population(population_size, bounds) best_fitness_over_time = [] for generation in range(generations): # 评估种群适应度 fitness = evaluate_population(population) best_fitness_over_time.append(max(fitness)) # 选择 selected_population = select(population, fitness) # 生成新种群 new_population = [] for i in range(0, len(selected_population), 2): parent1 = selected_population[i] parent2 = selected_population[i+1] child1, child2 = crossover(parent1, parent2) new_population.append(mutate(child1, mutation_rate, bounds)) new_population.append(mutate(child2, mutation_rate, bounds)) population = new_population # 返回最佳个体及其适应度随时间变化 best_individual = max(population, key=objective_function) return best_individual, best_fitness_over_time# 参数设置bounds = [0, 10]population_size = 20generations = 50mutation_rate = 0.1# 执行遗传算法best_solution, fitness_over_time = genetic_algorithm(objective_function, bounds, population_size, generations, mutation_rate)# 输出最佳解best_solution_value = objective_function(best_solution)# 绘制适应度变化图plt.plot(fitness_over_time)plt.xlabel('Generation')plt.ylabel('Best Fitness')plt.title('Genetic Algorithm Optimization')plt.show()best_solution, best_solution_value3.2运行结果
Result(2.312058920926045, 13.902619229870472)(1)运行结果
最佳解:x≈2.31x \approx 2.31x≈2.31目标函数值:f(x)≈13.90f(x) \approx 13.90f(x)≈13.90(2)适应度变化图
适应度变化图如下所示:

3.3结果分析
最佳解与目标函数值:
遗传算法找到了函数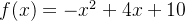 的最大值点
的最大值点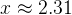 。目标函数值在该点的值为
。目标函数值在该点的值为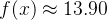 ,这是该函数的最大值。
,这是该函数的最大值。 适应度变化图:
图中显示了每一代的最佳适应度值,适应度值逐渐上升并趋于稳定。适应度值的上升表示种群中个体质量的提升,算法逐步逼近最优解。通过上述步骤,遗传算法成功找到了优化问题的近似最优解,并且从适应度变化图可以看到算法的收敛过程。如果对最终结果不满意,可以尝试调整参数(如种群规模、变异率等)以获得更好的结果。