
文章目录
一、 AVL的概念二、AVL树的实现1. AVL树结构定义2. 插入1)插入遍历逻辑控制2)插入什么时候需要控制平衡?3)旋转逻辑 总结
今天我们开始学习AVL树???
<( ̄︶ ̄)↗[GO!] <( ̄︶ ̄)↗[GO!] <( ̄︶ ̄)↗[GO!]
一、 AVL的概念
定义与特性:AVL树是最早发明的自平衡二叉查找树,是一棵空树或具备以下特性的二叉搜索树:其左右子树均为AVL树,且左右子树高度差的绝对值不超过1。因此,AVL树是一棵高度平衡的二叉搜索树,通过控制高度差实现平衡。
命名由来:AVL树得名于其发明者G. M. Adelson-Velsky和E. M. Landis,他们是两位前苏联科学家,于1962年在论文《An Algorithm for the Organization of Information》中提出了这一概念。
平衡因子的引入:在AVL树中,每个结点都有一个平衡因子(Balance Factor),定义为右子树高度减去左子树高度。其取值范围为-1、0、1。虽然AVL树并不强制要求平衡因子,但平衡因子便于观察和维护树的平衡状态,如同风向标的作用。
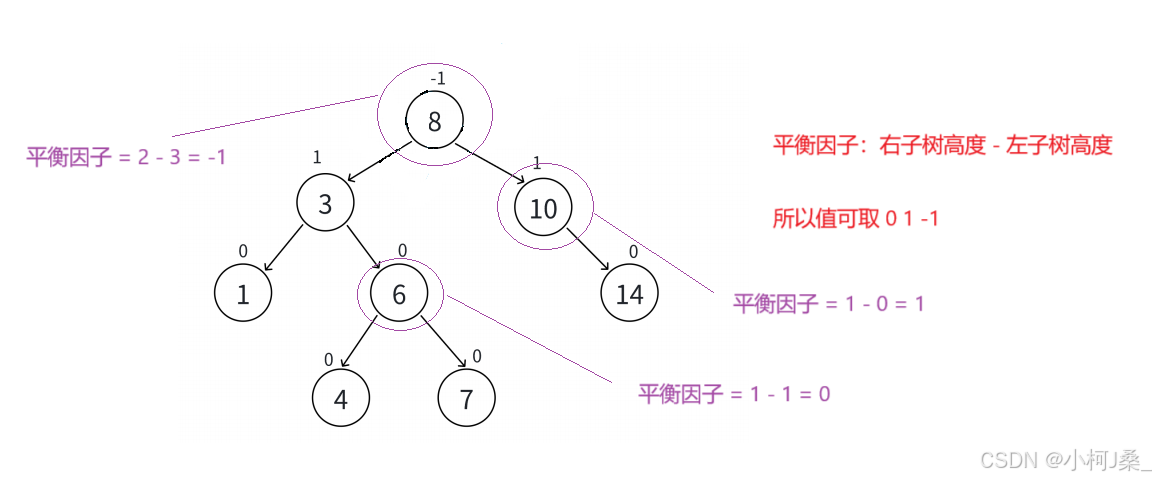
高度差要求的原因:AVL树的高度差要求不超过1,而非严格为0,因为在某些情况下(例如树包含2个或4个节点时),高度差为0无法实现,而高度差为1是最佳平衡状态。

二、AVL树的实现
1. AVL树结构定义
#pragma once#include<iostream>using namespace std;template<class K, class V>struct AVLTreeNode{pair<K, V> _kv; // 数据的存储AVLTreeNode<K, V>* _left; // 左孩子AVLTreeNode<K, V>* _right; // 右孩子AVLTreeNode<K, V>* _parent; // 父结点AVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}};template<class K, class V>class AVLTree{typedef AVLTreeNode Node;public:private:Node* _root = nullptr;};2. 插入
1)插入遍历逻辑控制
首先,第一部分,与set,map的插入是一样的,小于往右走,大于往左走。
bool insert(const pair<K, V>& kv){// 树为空,直接插入然后返回if (_root = nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){// 小于往左走if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first) // 大于往右走{parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);// 链接if (cur->_kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 通过平衡因子控制平衡return true;}2)插入什么时候需要控制平衡?
接下来就是控制平衡的逻辑
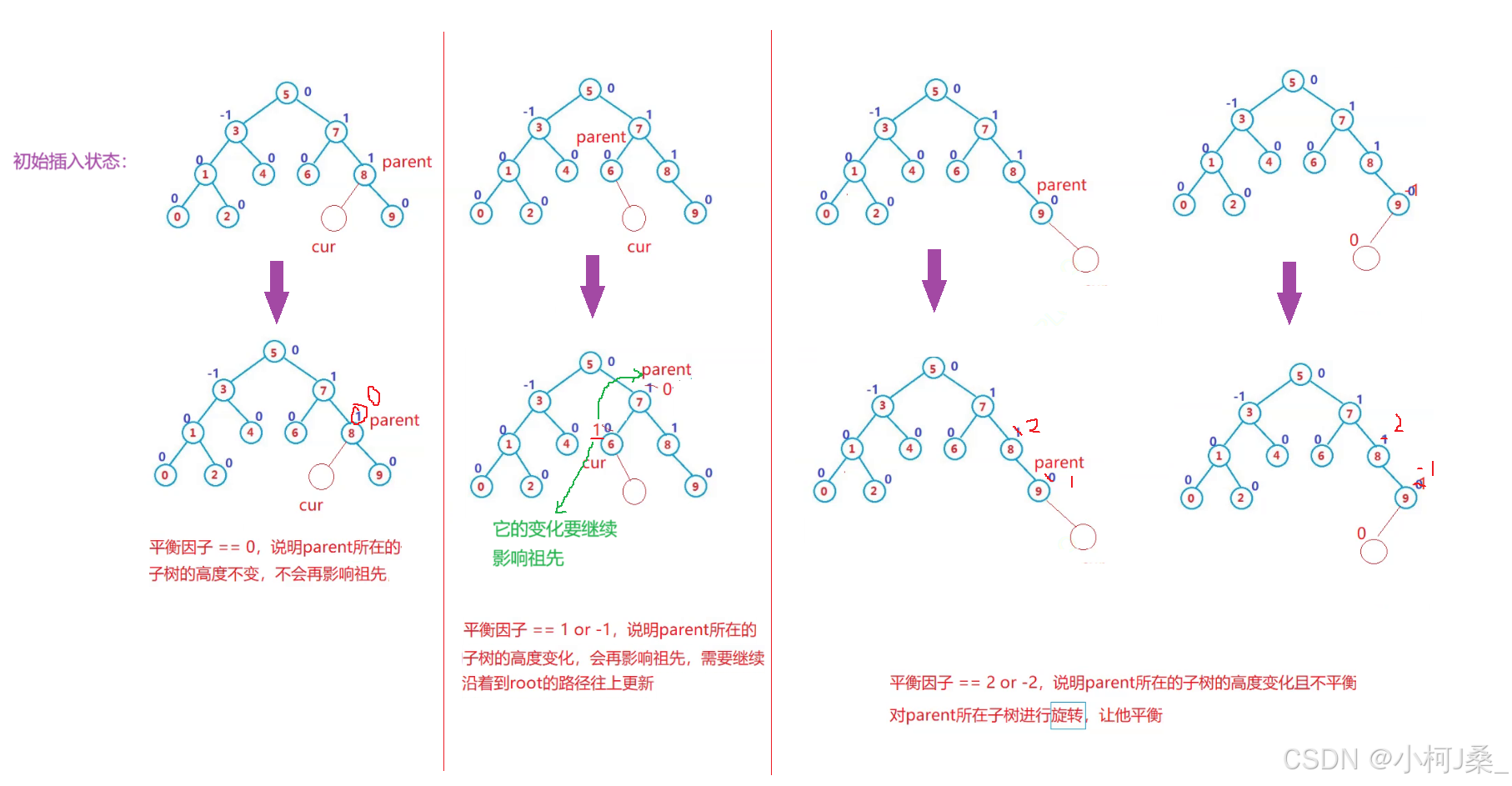
接下来,一张图,带你搞明白这里所有的逻辑!!!
控制平衡逻辑总结:
新增在左,parent平衡因子减减新增在右,parent平衡因子加加更新后parent平衡因子 == 0,说明parent所在的子树的高度不变,不会再影响祖先,不用再继续沿着到 root 的路径往上更新更新后parent平衡因子 == 1 or -1,说明parent所在的子树的高度变化,会再影响祖先,需要继续沿着到root的路径往上更新更新后parent平衡因子 == 2 or -2,说明parent所在的子树的高度变化且不平衡,对parent所在子树进行旋转,让他平衡更新到根节点会停止,也就是parent == nullptr 我们有如下这几种情况:
控制代码如下:
// 通过平衡因子控制平衡while (parent) // 如果parent为空,就停止{if (cur == parent->_left){parent->_bf--; // 如果新加入的结点在左侧,父亲平衡因子减1}else{parent->_bf++; // 如果新加入的结点在右侧,父亲平衡因子加1}if (parent->_bf == 0){break; // 父亲平衡因子为0,更新结束}else if (parent->_bf == 1 || parent->_bf == -1){// 继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要进行旋转调整}else{assert(false);}}3)旋转逻辑
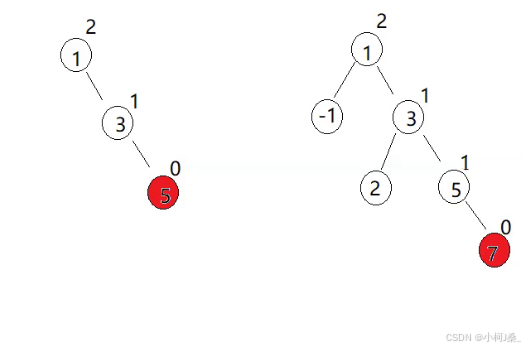
本篇文章我们先来看这样的一种情况,剩下的情况我们下次进行解析:
比如我们要进行左单旋,旋转如下这种情况:
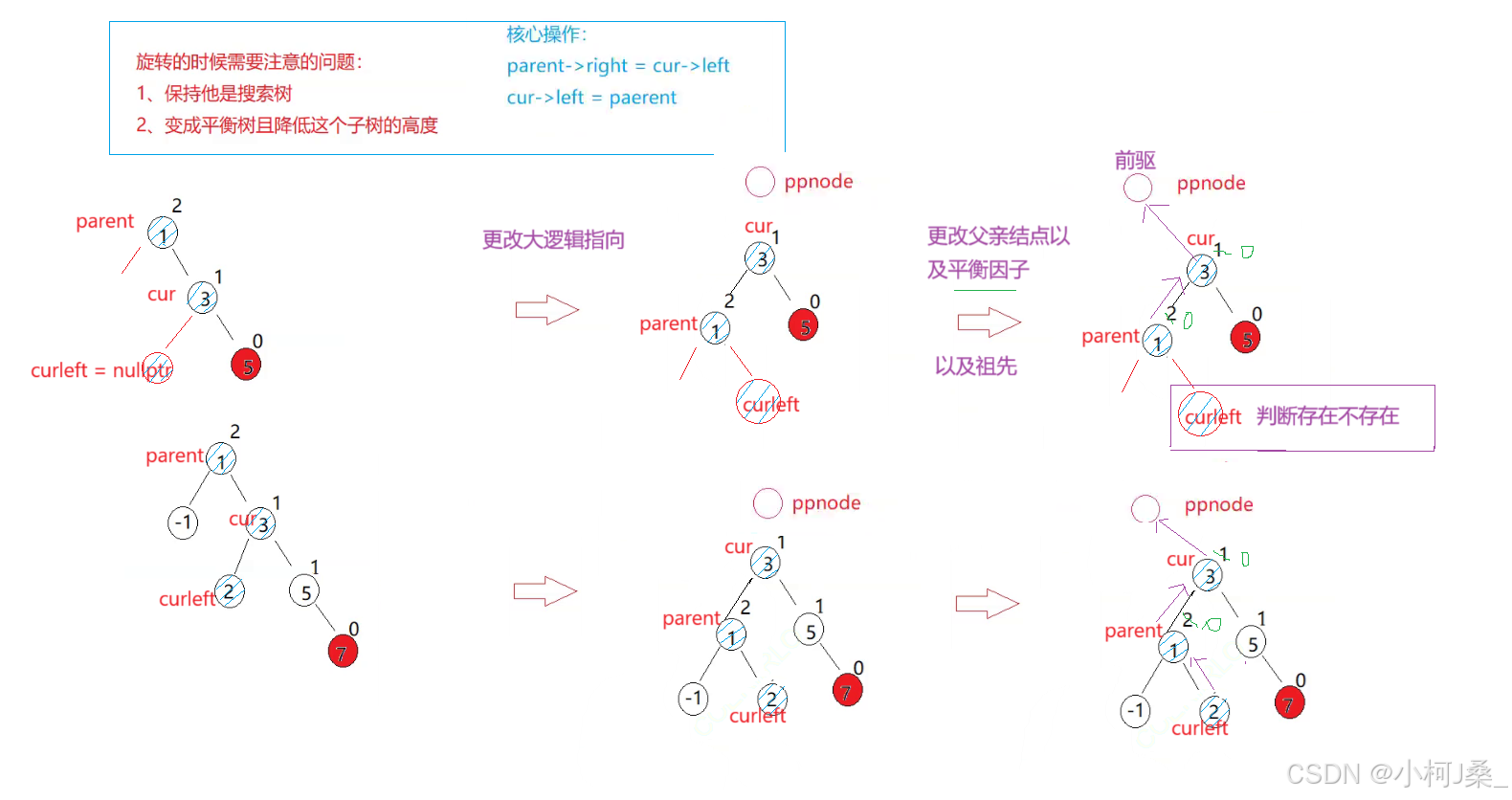
旋转的时候需要注意的问题 !
核心操作:
parent->right = cur->left
cur->left = parent
// 左单旋void Rotatel(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;// 重新链接parent->_right = curleft;if (curleft) // 如果curleft存在{curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left = parent){ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}// 更改平衡因子parent->_bf = cur->_bf = 0;}总结
到这里我们AVL第一部分就结束啦!!!
小小总结一下~???
AVL树是一种自平衡的二叉搜索树,以其发明者G. M. Adelson-Velsky和E. M. Landis命名。它通过严格控制左右子树的高度差(绝对值不超过1)保持平衡,从而显著提升增删查改操作的效率。每个节点的平衡因子帮助判断树的平衡状态,其范围为-1、0、1,便于观察与维护。虽然严格的高度平衡(差为0)在某些情况下不可实现,但AVL树的高度接近完全二叉树,因此效率可以稳定在 (O(log n))。这种高度平衡的设计,使AVL树成为效率优于普通二叉搜索树的重要数据结构。
