前言
注意,本文自10.12日起,正在每周2次更新的过程中,包括已写的部分也在不断修改(以增加更多技术细节、更加通俗易懂)
预计11月下旬完成第一版,12月底修订到第二版——具体修订记录详见本文文末..
可能是去年写或讲的关于ChatGPT原理的文章和课程,影响力太大了
导致自从OpenAI o1出来后,每过两天,就有朋友问,“校长 o1啥时候出解读或课程”,实在是各个大模型项目上的事情太多,加之近期一直在抠机器人(比如本博客内连发了五篇机器人相关的文章,再不刻意强插一下比如o1,真的很难停下来)
但,今天又有朋友来问,故,准备并行开写o1了
一开始,我主要是看的这几个资料
OpenAI o1的技术blog张俊林老师的Reverse-o1:OpenAI o1原理逆向工程图解GitHub上的o1论文列表,以及我自己挖掘到的一系列paper,以下是逐一出现在本文中的其中几篇1) 22年1月,Google,思维链的开山之作
Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
2) 23年4月,Google deepmind等机构,代码层面上让模型学会自我调试
《Teaching Large Language Models to Self-Debug》
3) 24年2月,斯坦福、Google等,如何通过CoT让模型学会解决复杂的数学问题
《Chain of Thought Empowers Transformers to Solve Inherently Serial Problems》,
4) 23年5月,让模型学会拆解问题
《Tree of Thoughts (ToT): Deliberate Problem Solving with Large Language Models》
5) 23年5月,OpenAI,《Let's Verify Step by Step》
6) 24年5月,通过结果监督的手段达到过程监督的效果
《Training Large Language Models for Reasoning through Reverse Curriculum Reinforcement Learning》
7) 22年3月,斯坦福、Google,可以迭代利用少量的推理示例和一个没有推理过程的大型数据集,以逐步增强执行更复杂推理的能力
《STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning》
8) 24年3月,斯坦福,语言模型可以教会自己在说话前先思考,即先想好再回答
《Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking》
9) 24年7月,来自Carnegie Mellon University、UC Berkeley、3MultiOn的研究者们提出了一种名为递归自省的方法——RISE
《Recursive introspection: Teaching language model agents how to self-improve》
10) 24年9月下旬,Google开发了一种不需要这些要求的有效自我纠正方法,称为通过强化学习进行自我纠正(Self-Correction via Reinforcement Learning,简称SCoRe)
《Training Language Models to Self-Correct via Reinforcement Learning》
11) 24年8月份,来自UC Berkeley、Google DeepMind的研究者证明在加强模型的推理能力方面,延长思考时间比单纯增加模型参数更有效
《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters》
12) 24年9月初,《Planning In Natural Language Improves LLM Search For Code Generation》
13) 24年5月,《Monte Carlo Tree Search Boosts Reasoning via Iterative Preference Learning》公号或某乎上的一些o1文章上交团队的一个o1复现
但随着本文越写越深,挖出来的相关资料也越来越多,我会竭尽所能,确保本文具备以下两大特征
尽可能在本文中把o1的所有重要细节都一次性说清楚如果实在有些细节因为篇幅而没法面面俱到的,我也会尽可能提供相关的论文供相关的读者进一步深入在行文过程中,对每一个结论都不做随意的主观猜测
由于OpenAI实在是不够开放,一个技术报告完全是啥都没说,所以很容易引发各种猜测、推测,虽然我没法完全百分百知晓o1的所有技术细节,但本文会尽可能做到一切结论都有科学而严谨的权威论文做佐证
且在实在必须做一定的推测时,也可能确保是合理、有信服力的猜测,而非主观想象
至于,为何要写OpenAI o1呢,简言之,就是能力强大
其在物理、化学和生物学的具有挑战性的基准任务上的表现与博士生相似且它在数学和编码方面表现出色。在国际数学奥林匹克 (IMO) 资格考试中,GPT-4o 仅正确解决了 13% 的问题,而推理模型得分为 83%,并在 Codeforces 比赛中达到了第 89 个百分位
第一部分 如何让模型学会思考并分解问题
1.1 如何让模型学会自我调试、解决复杂数学问题
说到o1的原理,根据OpenAI o1的技术报告显示
在于大规模强化学习算法教会o1如何在高质量高效数据(data-efficient)的训练过程中利用其CoT(chain of thought)的能力进行有效思考。且他们发现,随着强化学习的更多赋能(训练时间计算)和思考时间的增加(测试时间计算),o1 的性能会持续提高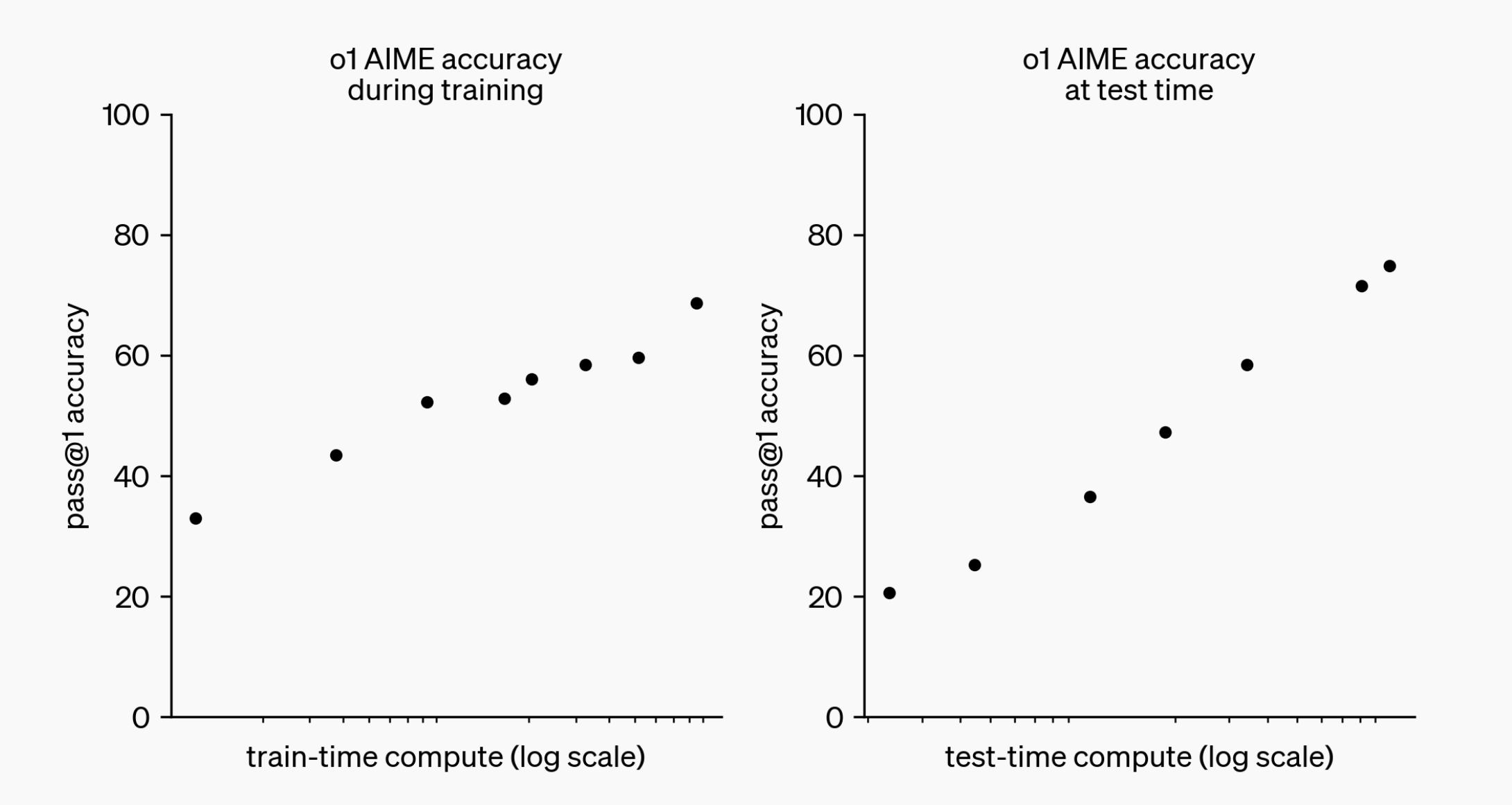
Similar to how a human may think for a long time before responding to a difficult question, o1 uses a chain of thought when attempting to solve a problem.
相当于在面对一个不是很轻松的问题时,模型会像人类一样,尽可能思考全面,以想出一个万全之策那如何思考出来万全之策呢,OpenAI的策略是通过强化学习,让o1 学会优化其思维链并改进所使用的策略
Through reinforcement learning, o1 learns to hone its chain of thought and refine the strategies it uses.
接下来关键点来了
1) 它学会了识别并纠正自己的错误,即It learns to recognize and correct its mistakes.
2) 将复杂的步骤分解成更简单的步骤,即It learns to break down tricky steps into simpler ones.
3) 并在当前方法无效时尝试不同的解决方式,即It learns to try a different approach when the current one isn’t working.
每一点都是职场精英人士的优秀特征啊,总之,整个过程显著提升了模型的推理能力
至于什么是CoT,特援引此文《ChatGPT技术原理解析:从RL之PPO算法、RLHF到GPT4、instructGPT》中“2.4.3 基于思维链(Chain-of-thought)技术下的prompt,是后来OpenAI o1的关键技术之一的”这段内容
为让大语言模型进一步具备解决数学推理问题的能力,22年1月,谷歌大脑团队的Jason Wei、Xuezhi Wang等人提出了最新的Prompting机制——Chain of Thought(简称CoT)
简言之就是给模型推理步骤的prompt,让其学习人类如何一步步思考/推理,从而让模型具备基本的推理能力,最终可以求解一些简单甚至相对复杂的数学推理能力其对应的论文为,通过此篇论文《Chain-of-Thought Prompting Elicits Reasoning in Large Language Models》该论文全部作者包括Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Brian Ichter, Fei Xia, Ed Chi, Quoc Le, Denny Zhou
PS,上面的最后一位作者Denny zhou是Google deepmind推理团队的首席科学家
以下是一个示例(下图左侧为standard prompting,下图右侧为基于Cot的prompt,高亮部分为chain-of-thought),模型在引入基于Cot技术的prompt的引导下,一步一步算出了正确答案,有没有一种眼前一亮的感觉?相当于模型具备了逻辑推理能力
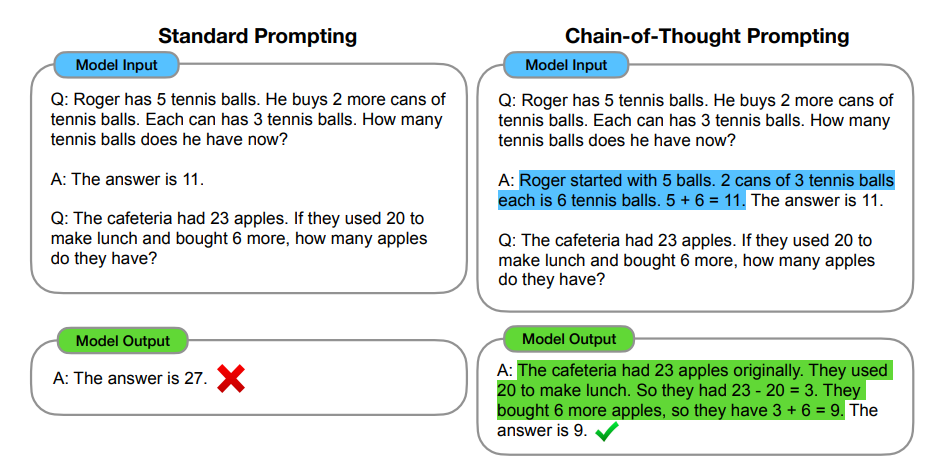
1.1.1 代码层面上让模型学会自我调试:Teaching LLM to Self-Debug by23年4月
23年4月份,来自Google deepmind、UC Berkeley的研究者们Xinyun Chen, Maxwell Lin, Nathanael Schärli, Denny Zhou(此人是Founder and lead of the Reasoning Team in Google DeepMind, 这是其个人主页:https://dennyzhou.github.io/ ),发布了此篇论文:Teaching Large Language Models to Self-Debug
在这项工作中,他们提出了自我调试方法,教大模型通过少样本提示来调试其预测的代码。且无需额外的模型训练,自我调试指导模型执行代码,然后根据代码及其执行结果生成反馈信息。与之前利用人为反馈进行代码修复的工作不同(那些工作中的反馈信息解释了代码错误及其修复方法)具体如下图所示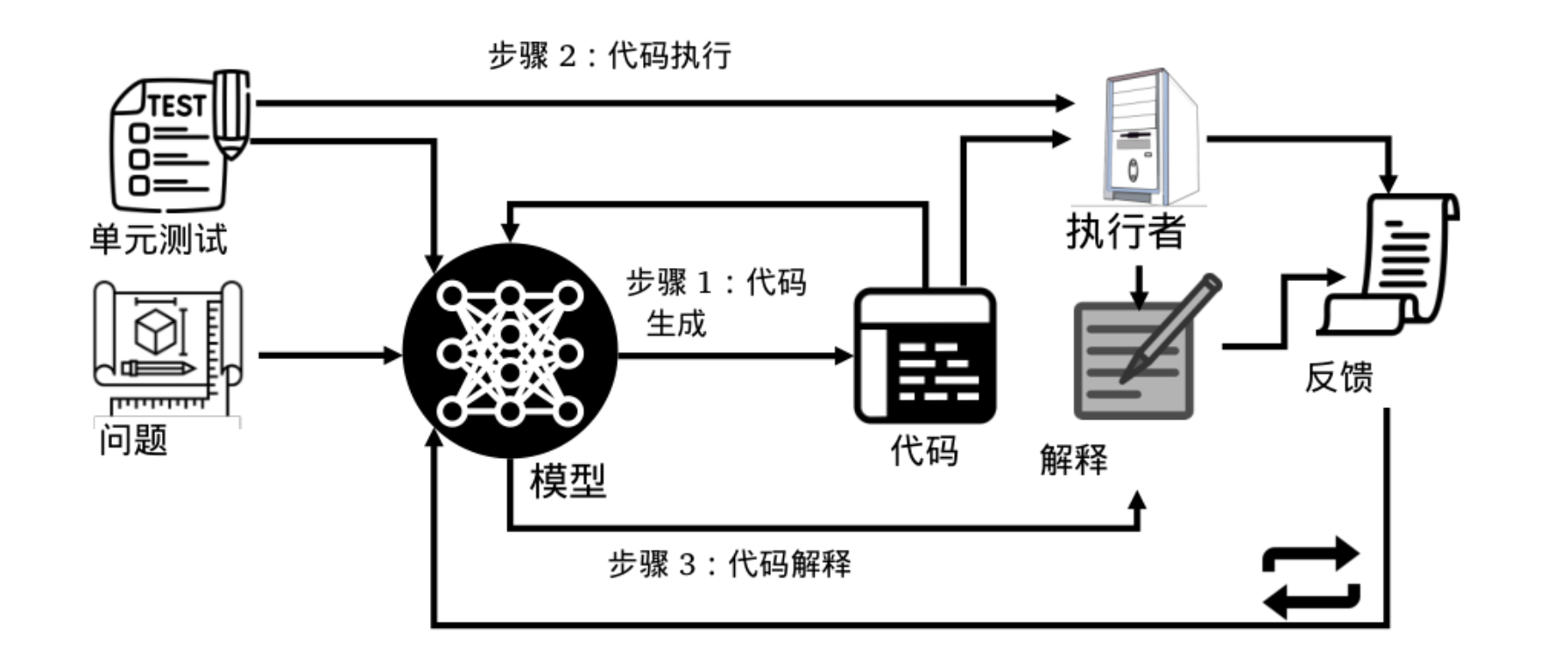
在有单元测试可用的代码翻译和文本到Python生成任务中,SELF-DEBUGGING显著提高了基线准确率,最高可达12%
总之,一次自我调试包含3个步骤:生成、解释和反馈
在生成步骤中,给定问题描述,模型预测候选程序在解释步骤中,模型被提示以语义上有用的方式处理预测结果,例如用自然语言解释预测,或为预测的代码创建一个示例输入的执行跟踪最后,在反馈步骤中,会生成一条关于预测代码正确性的反馈信息。这可以通过询问模型本身来确定,也可以通过单元测试外部生成当然,调试过程在反馈信息表明预测正确时终止,或者达到允许的最大调试次数时终止
接下来,再讨论下可以自动获取和生成的不同类型的自我调试反馈
简单反馈最简单的自动反馈形式是一个仅仅指示代码正确性的句子,而不提供更多详细信息,这省略了完整自我调试过程中的解释步骤
例如,在文本到SQL的生成中,少样本提示为所有正确的SQL查询提供反馈信息“上面的SQL预测是正确的!”,而对于错误的预测则是“上面的SQL预测是错误的。请修正SQL。”单元测试反馈(UT)
对于问题描述中包含单元测试的代码生成任务,除了利用代码执行来检查代码的正确性之外,我们还可以将执行结果纳入反馈中,这为调试提供了更丰富的信息
下图展示了一个示例单元测试反馈信息(左对齐的块是模型预测,右对齐的块包含输入的C++代码和基于代码执行的反馈信息)
 直观地查看运行时错误和失败单元测试的执行结果也有助于人类程序员更有效地调试。说明了只要有单元测试可用,利用它们可以持续提升自我调试性能代码解释反馈(Expl)
直观地查看运行时错误和失败单元测试的执行结果也有助于人类程序员更有效地调试。说明了只要有单元测试可用,利用它们可以持续提升自我调试性能代码解释反馈(Expl)尽管最近有令人鼓舞的进展表明,大型语言模型可以生成批评以避免产生有害的模型输出,并在一些自然语言任务上提高其性能,但先前的工作尚未展示模型生成反馈在代码生成中的有效性
另一方面,大型语言模型已被证明能够以文本和代码格式描述其生成的问题解决方案执行跟踪反馈(Trace)
除了解释代码本身,人类程序员通常还通过模拟执行过程来理解代码的语义意义。之前关于代码修复的研究表明,在执行跟踪上训练修复模型可以提高调试性能
因此,当单元测试可用时,作者会检查另一种解释反馈格式,其中LLM被指示逐行解释中间执行步骤。请注意,执行跟踪和逐行解释都来自模型生成,而不是代码执行,因此跟踪反馈不需要比纯代码解释反馈更多的信息;即,不需要访问中间执行状态
以下是一个用于文本到 SQL 生成的自我调试提示示例,其中SQL 查询、解释和反馈均由模型预测(当返回的表格有超过 2 行时,提示中仅包含前 2 行)

1.1.2 如何通过CoT让模型学会解决复杂的数学问题 by24年2月
24年2月,当时来自斯坦福大学、芝加哥丰田技术研究所、谷歌的研究者们Zhiyuan Li, Hong Liu, Denny Zhou, Tengyu Ma,发布了这篇论文《Chain of Thought Empowers Transformers to Solve Inherently Serial Problems》
在该论文中,作者展示了配备CoT的Transformer——允许Transformer在回答问题之前自回归地生成一系列中间token——可以解决固有需要串行计算的复杂问题(假设复杂性理论中的一些知名猜想)We then show that transformers equipped withCoT—allowing the transformer to auto-regressively generate a sequence of intermediate tokens before answering the questions—can solve complex prob-lems that inherently require serial computations (assuming well-known conjectures in complexity theory).直观地说,没有CoT,Transformer进行的串行计算数量受限于深度(在此工作中被视为一个固定常数),而有了T个中间步骤,可能的串行计算数量增加到T
Intuitively, without CoT, the number of serial computations conducted by the transformeris bounded by the depth (which is considered as a fixed constant for this work), whereas with T in termediate steps, the number of serial computations possible is boosted to T.
注意,随着序列长度的增加,T可以轻松增加,而深度是依赖于架构的一个固定数值
Note that T caneasily increase as the sequence length increases where the depth is a fixed number that depends onthe architecture
// 待更
1.2 如何让模型学会分解问题
1.2.1 Decomposed Prompting: A Modular Approach for Solving Complex Tasks
22年10月,Decomposed Prompting: A Modular Approach for Solving Complex Tasks
概述:提出了一种名为Decomposed Prompting的方法,通过将复杂任务分解为更简单的子任务,并将这些子任务委托给专门处理这些子任务的LLMs。该方法的模块化结构允许每个提示针对其特定的子任务进行优化,并在必要时进一步分解
// 待更
1.2.2 Tree of Thoughts (ToT): Deliberate Problem Solving with Large Language Models
23年5月,Tree of Thoughts (ToT): Deliberate Problem Solving with Large Language Models
// 待更
1.3 如何让模型学会一步一步的自我验证:结合结果监督与过程监督
1.3.1 Let's Verify Step by Step(含ORM、PRM的介绍)
首先,我们来回顾下语言生成的整个过程
在每个时间步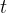 ,策略语言模型
,策略语言模型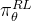 由参数
由参数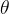 参数化的策略接收一个状态
参数化的策略接收一个状态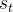 ,该状态由输入prompt和到目前为止生成的文本组成
,该状态由输入prompt和到目前为止生成的文本组成然后,策略的行动
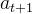 是在该状态
是在该状态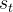 的条件下生成下一个token,其概率为
的条件下生成下一个token,其概率为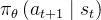
之后,环境返回一个奖励
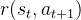 ,状态以转移概率
,状态以转移概率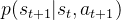 转移到
转移到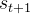 强化学习的目标是找到一个最优策略,以最大化轨迹
强化学习的目标是找到一个最优策略,以最大化轨迹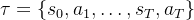 上的累积奖励(即回报),其中
上的累积奖励(即回报),其中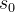 是初始状态(即提示),
是初始状态(即提示),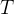 是动作的长度
是动作的长度策略梯度的一般形式给出如下
![\mathbb{E}_{\tau \sim \pi_{\theta}^{\mathrm{RL}}}\left[\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}^{\mathrm{RL}}\left(a_{t} \mid s_{t-1}\right) R\left(s_{t-1}, a_{t}\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120127173259368723008.png)
其中
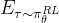 表示在从策略
表示在从策略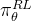 采样的轨迹分布下的期望
采样的轨迹分布下的期望且其中回报
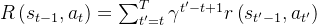 是从时间步骤
是从时间步骤 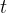 开始的奖励的折现和,折现因子为
开始的奖励的折现和,折现因子为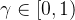
通过这个梯度,可以进行梯度上升来优化模型。如果回报是有利的,动作的选择概率会通过增加来“增强”如果给定一个数据集
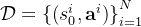 ,其中包含
,其中包含 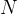 对输入
对输入 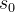 和人类生成的输出序列
和人类生成的输出序列 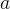 ,其中
,其中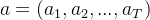 ,整个轨迹为
,整个轨迹为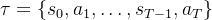
策略梯度则变为
![\begin{array}{l} \mathbb{E}_{s_{0} \sim \mathcal{D}}\left[\mathbb{E}_{\tau \sim \pi_{\theta}^{\mathrm{RL}}\left(\cdot \mid s_{0}\right)}[ \right. \\ \left.\left.\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}^{\mathrm{RL}}\left(a_{t} \mid s_{t-1}\right) R\left(s_{t-1}, a_{t}\right)\right]\right] \end{array}](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120129173259368941692.png)
当然,如果你对上面的这些还不太明白,则可以看下此文《强化学习极简入门:通俗理解MDP、DP MC TC和Q学习、策略梯度、PPO》
其次,近年来,大型语言模型在执行复杂的多步推理方面有了很大提升。然而,即使是最先进的模型仍然经常会产生逻辑错误,很容易出现一步错、则步步错的情况
所以,为了训练更可靠的模型,可以
选择:结果监督的奖励模型ORMs它仅为采样序列的最终结果提供反馈
即奖励模型只给最后一个结果分配奖励分数,而其他token的分数为0
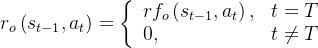
所以其可以在没有人类参与的情况下进行,针对所有待解决的问题自动得到答案或选择:过程监督的奖励模型PRMs
它为每个中间推理步骤提供反馈,即奖励模型
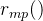 被训练用于为每个中间推理步骤分配一个奖励分数
被训练用于为每个中间推理步骤分配一个奖励分数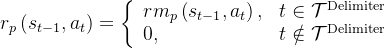
如此则能够准确指出错误发生的位置
但该PRM则需要依赖于人工标注以提供过程监督,比如告诉模型每一步的正确与否,比如下图
ORM 在最后一个标记上的预测作为解决方案的整体得分,这点大家可能并不陌生了,因为instructGPT便是这么做的(详见这篇ChatGPT原理笔记)
而PRM好像很少见,有人可能会说,在这篇ChatGPT原理笔记中,在讲到DSC的实现时,不讲到了虽然奖励模型RM的输出结果reward侧重结果监督奖励,但critic输出的价值估计value则侧重衡量过程么
举个例⼦,假定在经验数据池里,有seq=[ i am learning machine learning with julyedu ],其
KL系数,即βkl_ctl: 0.02旧策略下生成句子中不同词的对数概率
log_probs: [-12.0938, -20.1250, -1.3477, -1.8945, -0.9966, -0.5142, -1.4902]SFT策略下生成句子中不同词的对数概率
ref_log_probs: [-12.1172, -20.1406, -1.3447, -2.1699, -1.2002, -0.7905, -1.6611]KL = - kl_ctl * (log_probs - ref_log_probs)
kl_divergence_estimate: [-4.6873e-04, -3.1257e-04, 5.8591e-05, -5.5084e-03, -4.0741e-03, -5.5275e-03, -3.4180e-03]rewards = [0, 0, 0, 0, 0, 0, reward_score]
token_id为7的token作为该对话的最后1个有效token,其对应的实际经验奖励reward_score将被⽤于表示整个对话的reward
即其奖励reward_score只会是1个标量
reward_clip(reward_score)
reward_clip: -0.0826KL[最末有效token的idx] + reward_clip → KL_rewards
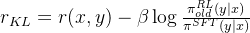
然后才有后来的优势值计算结果
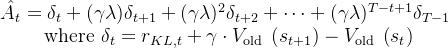
以及
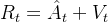
最后,再有critic输出的价值估计Value对returns的拟合
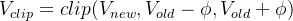
![vf\_loss = \frac{1}{2} \cdot E_{\tau \sim \pi_{old}^{RL}} E_{s_t \sim {\tau}} [\max((V_{new}(s_t)-R_t)^2, (V_{clip}(s_t)-R_t)^2)]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120130173259369098166.png)
其实不然,原因在于
prm orm本质都是奖励模型 给出实际得分评判,他们本身如果需要都可以引入“critic”prm更倾向于表达“走到这一步是好还是坏”,只看这时候如何critic本质还是价值估计 给出的都是价值预测
而且更多时候critic会更倾向于表达“给定状态和动作,最后的奖励可能是多少”,侧重关注对未来的影响
进一步,23年5月,OpenAI的这篇论文《Let's Verify Step by Step》发现过程监督在训练模型解决具有挑战性的MATH数据集的问题时,明显优于结果监督,比如过程监督模型解决了MATH测试集代表性子集中的78%问题
那如何训练PRM呢,训练模型的第一步当然是收集数据了
为了收集过程监督数据,首先向人工数据标注员提供由模型回答数学问题的逐步解决方案
在每次迭代中,他们为每个问题生成N个解决方案,,且尝试在问题级别(每个问题K个解决方案)或在整个数据集上(总共K个解决方案,不均匀分布在各个问题中)应用这种前K过滤最终,将收集的步骤级标签的整个数据集称为PRM800K。PRM800K训练集包含针对12K个问题的75K个解决方案的800K个步骤级标签他们的任务是为解决方案中的每一步分配一个正面、负面或中性的标签,如下图所示
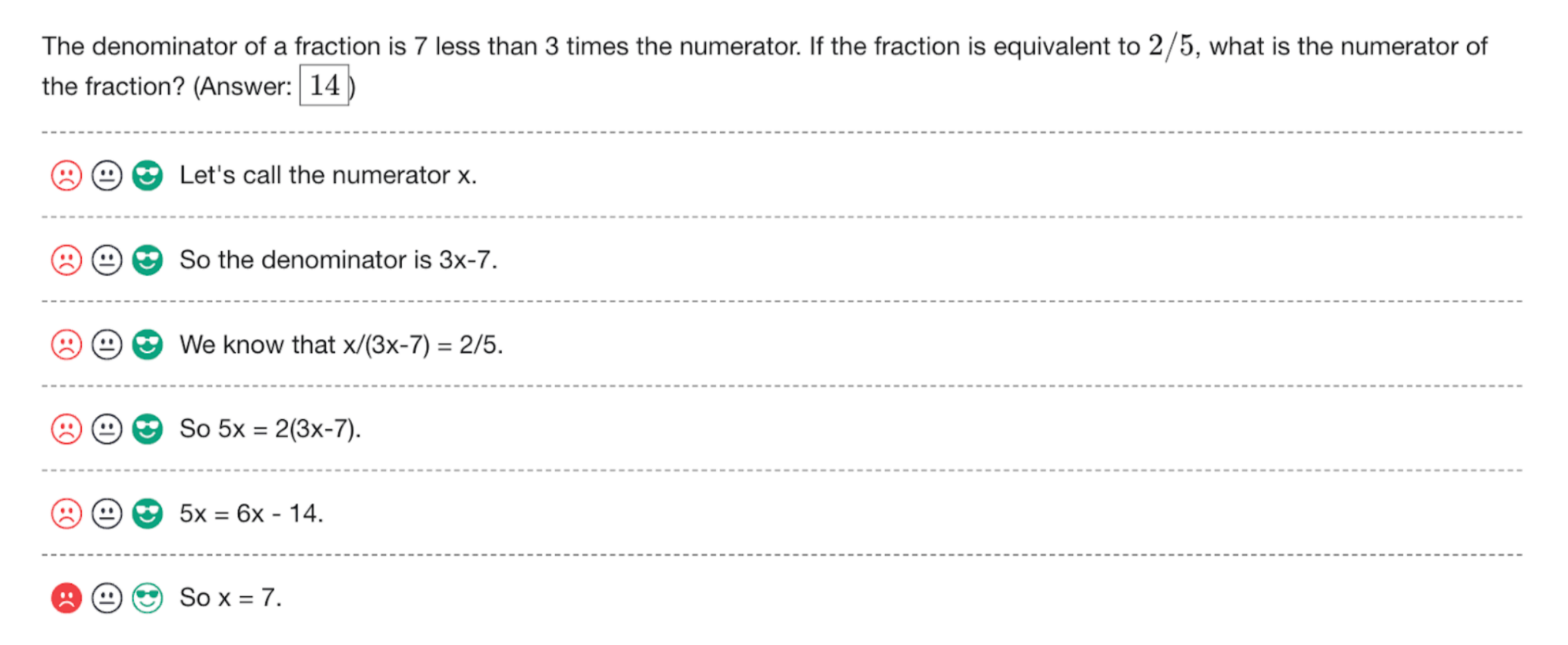
1.3.2 R3:通过结果监督的手段达到过程监督的效果 by24年5月
考虑到结果监督为最终结果提供稀疏的奖励,但不识别错误位置(没法明确哪些动作导致了成功或失败),而过程监督则提供逐步的奖励,但需要大量的人工标注

24年5月,来自复旦的研究者们(黄萱菁团队),通过此篇论文《Training Large Language Models for Reasoning through Reverse Curriculum Reinforcement Learning》提出了一种名为R3的创新方法:通过Curriculum RL进行逆向推理学习

该方法仅使用结果监督来实现大型语言模型的过程监督优势。在将RL应用于复杂推理时,核心挑战在于识别出能够获得正向奖励的动作序列,并提供适当的监督以进行优化
对于一个多跳推理问题,可以通过不同的推理路径得出一个标准答案
假设可以访问至少一个示例,即一个通往标准答案的正确推理路径,就像在监督微调中一样。当模型从初始状态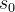 开始探索时,可能会遇到难以获得正奖励的问题
开始探索时,可能会遇到难以获得正奖励的问题
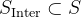 ,并让策略
,并让策略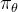 从接近目标状态的中间状态
从接近目标状态的中间状态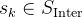 开始探索:
开始探索: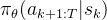 ,其中
,其中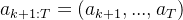
基于结果的奖励函数为最终结果提供反馈,作为在
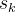 之后采取的动作的监督信号
之后采取的动作的监督信号在这种策略中,示范中
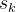 之前的轨迹(即
之前的轨迹(即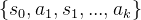 可以作为一种指导,帮助模型更容易获得正向奖励,并避免陷入无方向、低效的探索过程,如下图所示
可以作为一种指导,帮助模型更容易获得正向奖励,并避免陷入无方向、低效的探索过程,如下图所示 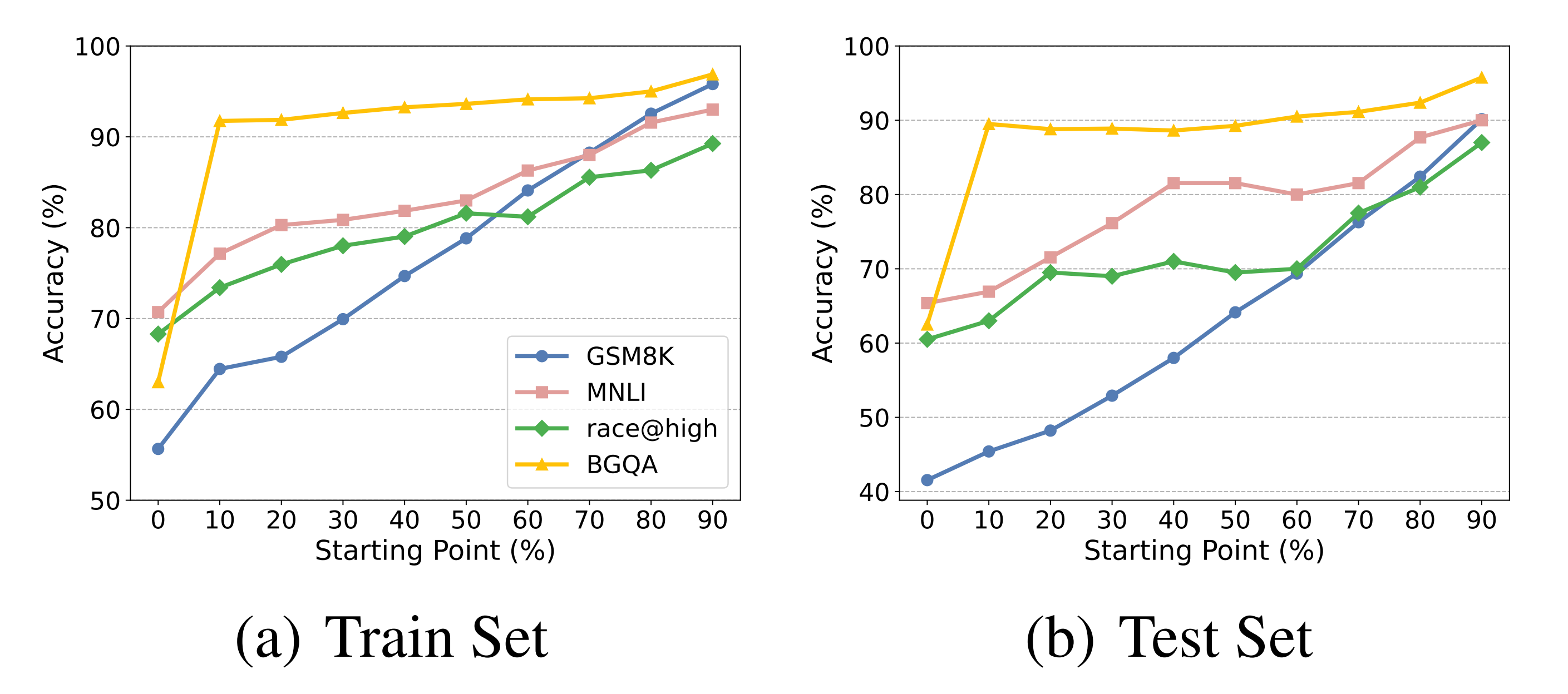
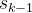 ),从而利用已经获得的知识
),从而利用已经获得的知识在每个阶段,模型面临一个容易的探索问题,因为它已经学会解决大部分剩余的部分,因此很可能成功。通过这种方式,可以形成一个逐步增加探索难度的curriculum
这使得能够为模型提供大致的逐步监督信号,现在,策略梯度可以表示为:
![\begin{array}{l} \mathbb{E}_{s_{k} \sim \mathcal{S}^{\text {Inter }}} {\left[\mathbb{E}_{\tau \sim \pi_{\theta}^{\mathrm{RL}}\left(\cdot \mid s_{k}\right)}[ \right.} \\ \left.\left.\sum_{t=k+1}^{T} \nabla_{\theta} \log \pi_{\theta}^{\mathrm{RL}}\left(a_{t} \mid s_{t-1}\right) R_{o}\left(s_{t-1}, a_{t}\right)\right]\right] \end{array}](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120134173259369475363.png)
其中,
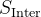 指的是从数据集
指的是从数据集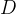 中采样的一个演示的中间状态集;
中采样的一个演示的中间状态集;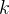 从
从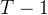 开始并逐步回退到
开始并逐步回退到 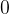 。在最后一步,模型开始从初始状态
。在最后一步,模型开始从初始状态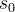 展开,这相当于原始的结果监督强化学习接下来,便可以通过PPO算法迭代策略,且设计奖励函数
展开,这相当于原始的结果监督强化学习接下来,便可以通过PPO算法迭代策略,且设计奖励函数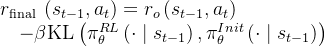
且和此文《ChatGPT原理》中3.2节介绍的DSC一样,通过广义优势估计GAE来计算优势
第二部分 自我推理验证出问题之后,如何让模型学会自我纠正
2.1 自我推理之Self-Taught Reasoner及其变体Quiet-STaR
2.1.1 STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning
22年3月,来自斯坦福、Google的研究者们(Eric Zelikman, Yuhuai Wu, Jesse Mu, Noah D. Goodman),提出了《STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning》
具体而言,作者使用少量示例提示大型语言模型自我生成推理过程,并通过对那些导致正确答案的推理进行微调,进一步提升模型的能力,然后重复这一过程,每次使用改进后的模型生成下一组训练集。这是一个协同过程,其中推理生成的改进提升了训练数据,而训练数据的改进又进一步提升了推理生成但作者发现上面这个循环最终无法解决训练集中任何新的问题,因为它没有收到针对未能解决的问题的直接训练信号为了解决这个问题,作者提出了合理化方法:对于每个模型未能正确回答的问题,他们通过提供正确答案来生成新的推理过程
这让模型能够逆向推理——给定正确答案,模型可以更容易地生成有用的推理过程
这些推理过程随后被收集为训练数据的一部分,通常可以提高整体准确性
总之,作者开发了自学推理者(Self-Taught Reasoner,简称STaR)方法,如下图所示

这是一种可扩展的自举方法,允许模型学习生成自己的推理,同时也学习解决日益复杂的问题
在该的方法中,重复以下过程:
具体实现过程如下
先有一个预训练的LLM和一个包含问题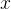 及其答案
及其答案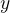 的初始数据集:
的初始数据集: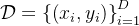
STaR的方法从一个包含中间推理过程
 的小提示集P开始:
的小提示集P开始: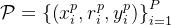
其中P≪D(例如P= 10)
类似于标准的少样本提示,然后将这个提示集合与D中的每个示例连接起来,即
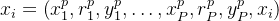 ,这鼓励模型为
,这鼓励模型为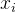 生成一个理由
生成一个理由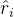 ,然后是一个答案
,然后是一个答案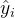
假设导致正确答案的理由比导致错误答案的理由质量更高。因此,过滤生成的理由,仅保留那些导致正确答案的理由——即
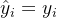 然后,在这个过滤后的数据集上微调基础模型
然后,在这个过滤后的数据集上微调基础模型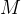 通过使用新微调的模型生成新的理由来重新开始这个过程
通过使用新微调的模型生成新的理由来重新开始这个过程不断重复这个过程,直到性能达到预期
注意,在这个过程中,一旦收集到一个新的数据集,便会从原始的预训练模型M开始训练,而不是持续训练一个模型,以避免过拟合
下图是算法概要/流程

总之,STaR可以被视为RL风格策略梯度目标的近似。要理解这一点,请注意,M可以被视为一个离散潜变量模型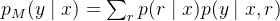 ——换句话说,
——换句话说,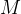 首先采样一个潜在的理性
首先采样一个潜在的理性 然后预测
然后预测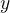
现在,给定指示器奖励函数![]() ,整个数据集上的总期望奖励为
,整个数据集上的总期望奖励为
![\begin{aligned} J(M, X, Y) & =\sum_{i} \mathbb{E}_{\hat{r}_{i}, \hat{y}_{i} \sim p_{M}\left(\cdot \mid x_{i}\right)} \mathbb{1}\left(\hat{y}_{i}=y_{i}\right), \\ \nabla J(M, X, Y) & =\sum_{i} \mathbb{E}_{\hat{r}_{i}, \hat{y}_{i} \sim p_{M}\left(\cdot \mid x_{i}\right)}\left[\mathbb{1}\left(\hat{y}_{i}=y_{i}\right) \cdot \nabla \log p_{M}\left(\hat{y}_{i}, \hat{r}_{i} \mid x_{i}\right)\right] \end{aligned}](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120138173259369825136.png)
梯度是通过策略梯度的标准对数导数技巧获得的。注意,指示函数会丢弃所有未能导致正确答案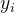 的采样理由的梯度:这是 STaR 中的过滤过程(如上面Algorithm 1 STaR第 5 行所示)。因此,STaR 通过以下方式近似
的采样理由的梯度:这是 STaR 中的过滤过程(如上面Algorithm 1 STaR第 5 行所示)。因此,STaR 通过以下方式近似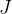
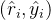 的样本,以减少此估计的方差(以可能导致对理由的偏见性探索为代价,即at the cost of potentially biasedexploration of rationales)以及在同一批数据上进行多次梯度步骤「类似于一些策略梯度算法 [25],即Proximal policy optimization algorithms——简称PPO」
的样本,以减少此估计的方差(以可能导致对理由的偏见性探索为代价,即at the cost of potentially biasedexploration of rationales)以及在同一批数据上进行多次梯度步骤「类似于一些策略梯度算法 [25],即Proximal policy optimization algorithms——简称PPO」 2.1.2 Quiet-STaR: 语言模型可以教会自己在说话前思考
24年3月,来自斯坦福的研究者(Eric Zelikman, Georges Raif Harik, Yijia Shao, Varuna Jayasiri, Nick Haber, Noah Goodman),提出此篇论文《Language Models Can Teach Themselves to Think Before Speaking》
在上一节的《自学推理者》(STaR, Zelikman et al. 2022)中,有用的思考是通过「从问答中的几个例子中推断基本原理,并从那些导致正确答案的例子中学习」来学习的In the Self-Taught Reasoner (STaR, Zelikman et al. 2022),useful thinking is learned by inferring rationales from few-shot examplesin question-answering and learning from those that lead to a correc tanswer.
这是一个高度受限的设置——理想情况下,语言模型可以学会在任意文本中推断未陈述的基本原理
This is a highly constrained setting – ideally, a language modelcould instead learn to infer unstated rationales in arbitrary text.故作者提出Quiet-STaR,这是STaR的一个推广版本,其中语言模型学习在每个token上生成理由(相当于在生成每个token时,都能生成一个为何生成当下token的“内心独白”或“理由”)以解释未来文本,从而改善其预测
We present Quiet-STaR, a generalization of STaR in which LMs learn to generate rationales at each token to explain future text, improving theirpredictions.
具体而言,Quiet-STaR的操作包括三个主要步骤,如下图所示
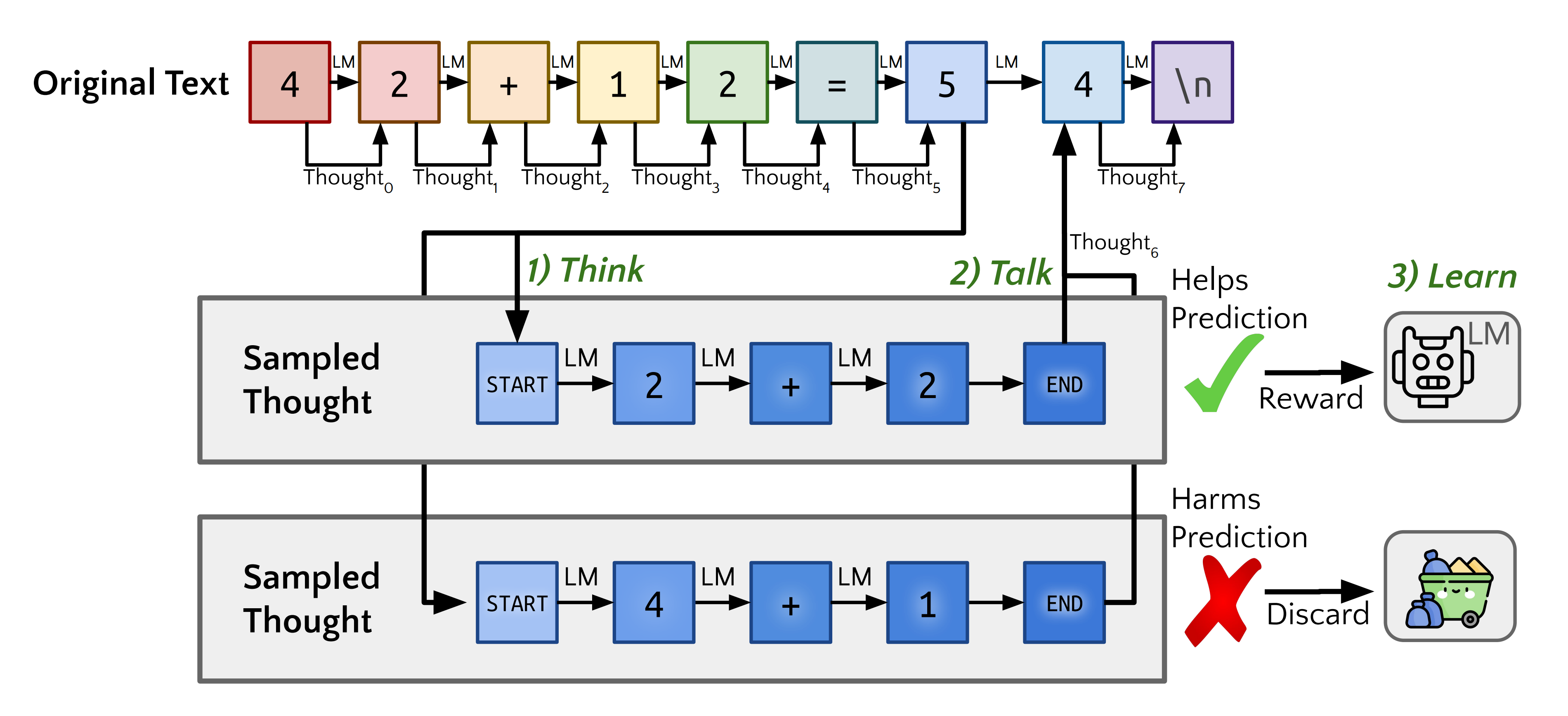
在输入序列
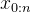 中并行处理每个标记
中并行处理每个标记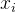 ,生成长度为
,生成长度为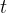 的推理:
的推理: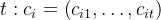 ,从而产生
,从而产生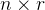 个推理候选
个推理候选插入学习到的<|startofthought|>和<|endofthought|>token来标记每个推理的开始和结束
In parallel across n tokens xi in an input sequence x0:n, we generate r rationales of length t: ci = (ci1, . . . , cit),resulting in n × r rationale candidates.
We insert learned <|startofthought|> and<|endofthought|> tokens to mark each rationale’s start and end.混合:后推理和基础预测,即Mixing post-rationale and base predictions
从每个推理后的隐藏状态输出中,作者训练一个“混合头”——一个浅层的多层感知机(MLP),生成一个权重,用于确定在多大程度上应该将基于推理后的下一个词预测的 logits 与基础语言模型预测的 logits 结合起来
由于引入了推理,这种方法在微调的早期阶段缓解了分布偏移
From the hiddenstate output after each rationale, we train a ”mixing head” – a shallow MLP produc-ing a weight determining how much the post-rationale next-token predicted logits should be incorporated compared to the base language model predicted logits. Thisapproach eases distribution shift early in finetuning, due to introducing rationales.优化理由生成,即Optimizing rationale generation
作者优化理由生成参数(开始/结束标记和语言模型权重),以增加使未来文本更可能出现的理由的概率
We optimize the rationale generation parameters (start/end tokens and LM weights) to increase the likelihoodof rationales that make future text more probable.
且使用REINFORCE为理由提供学习信号,基于它们对未来token预测的影响
为了减少方差,作者采用了一种教师强迫技巧,在损失中不仅包括预测思考之后的token的可能性,还包括预测后来的token的可能性
We use REINFORCE to providea learning signal to rationales based on their impact on future-token prediction.
To reduce variance, we apply a teacher-forcing trick to include in the loss thelikelihood of predicting not only the token after the thought but also later tokens
理论清楚了,咱们来看下代码实现

我觉得可能不少读者已经懵了,为方便大家一目了然,我给上面的代码逐行解读下(没有下面这个解读,你会觉得好难,有了这个解读,你会觉得原来这么好理解!)
准备阶段:需要一个初始的模型,一些训练数据,以及一些参数来控制训练的过程,比如学习的速度(学习率)和每次训练处理的数据量(批次大小)训练过程:反复进行训练,直到达到预定的训练步数。每一轮训练,都会取出一批数据# 训练过程,重复num_steps次
for i=0 to num_steps do
# 从输入序列 X 中抽取一个长度为 l 的批次
Sample batch of sequences X of length l
# 初始化隐藏状态
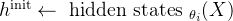 对于这批数据中的每个位置,都会做以下事情:
对于这批数据中的每个位置,都会做以下事情:# 对于序列中的每个位置
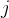 的token(使用并行和注意力掩码),都会生成推理并进行预测
的token(使用并行和注意力掩码),都会生成推理并进行预测for j=1 to l in parallel using attention mask do
首先,让模型预测接下来应该出现什么词
# 使用语言模型的头部预测下一个
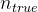 个token的概率,并计算初始的对数概率 log p_init
个token的概率,并计算初始的对数概率 log p_init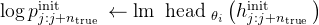
然后,让模型生成一些“思考”的内容,这些内容就像是模型在做出预测之前的“内心独白”
# 为序列X当前位置
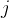 的token生成内在推理/思维
的token生成内在推理/思维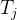 ,思维用 `<start_thought>` 和 `<end_thought>` 包裹,并生成 n_thoughts 个潜在思维
,思维用 `<start_thought>` 和 `<end_thought>` 包裹,并生成 n_thoughts 个潜在思维# 用 `<end_thought>` 标记生成思维的结束
接下来,把模型生成的“内心独白”和原始数据结合起来,再次让模型预测接下来的词
# 将生成的推理Tj与原始序列X结合,并更新隐藏状态
# 使用更新后的隐藏状态预测下一个
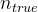 个token的概率,并计算计算带有思维的对数概率 log p_thought
个token的概率,并计算计算带有思维的对数概率 log p_thought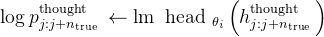 混合预测:结合模型的原始预测和带有“内心独白”的预测,得到一个综合的结果
混合预测:结合模型的原始预测和带有“内心独白”的预测,得到一个综合的结果# 使用混合头部计算一个权重,这个权重决定了原始预测和带有推理的预测在最终预测中所占的比例
 计算损失:我们会计算模型的预测和实际数据之间的差异,这个差异就是模型需要改进的地方
计算损失:我们会计算模型的预测和实际数据之间的差异,这个差异就是模型需要改进的地方# 计算混合后的对数概率,得到最终预测
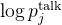

# 使用负对数似然计算损失函数,基于真实标签
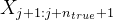 ,与最终的预测
,与最终的预测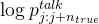 ——代表在位置 j 到 j+n_true 的预测
——代表在位置 j 到 j+n_true 的预测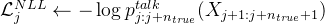 奖励机制:如果模型的预测因为加入了“内心独白”而变得更好,就会给它一些“奖励”,让它知道这样做是对的
奖励机制:如果模型的预测因为加入了“内心独白”而变得更好,就会给它一些“奖励”,让它知道这样做是对的# 计算REINFORCE奖励,这是带有推理的预测和原始预测之间的对数概率差异,我大胆估计一下,估计可能有朋友在这里不明白了,咋就
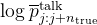 代表了模型初始状态下(没有使用思维推理推理部分)生成的对数概率,其实 伪代码么,加之
代表了模型初始状态下(没有使用思维推理推理部分)生成的对数概率,其实 伪代码么,加之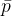 通常表示某种“基线”或“平均”值,故
通常表示某种“基线”或“平均”值,故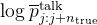 则用来代表模型在没有进行推理之前的基础预测概率了
则用来代表模型在没有进行推理之前的基础预测概率了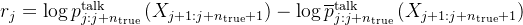
# 如果rj大于0——相当于引入思维后的预测结果比基础预测好「即
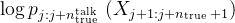 更高」,那么奖励 r_j 将是正值,表示模型得到了改进;否则,奖励为负值,表示没有改进或表现更差,使用REINFORCE奖励更新模型参数
更高」,那么奖励 r_j 将是正值,表示模型得到了改进;否则,奖励为负值,表示没有改进或表现更差,使用REINFORCE奖励更新模型参数![\nabla_\theta\mathcal{L}_j^{REINFORCE}\leftarrow-r_j 1[r_j>0]\cdot\nabla_\theta\log p_{\theta_i}(T_j|[X_{:j};<\text{start\_thought}>])](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120144173259370476790.png)
# 将NLL损失和REINFORCE损失相加,得到总损失
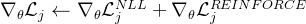 更新模型:根据损失和奖励,会调整模型的参数,让模型在下一次预测时做得更好
更新模型:根据损失和奖励,会调整模型的参数,让模型在下一次预测时做得更好# 使用梯度下降法更新模型参数
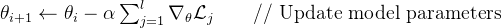
# 返回训练后的模型参数
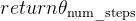
最后,重复以上步骤,直到模型训练完成
补充一下关于Quiet-STaR的三个主要步骤
首先是并行生成
Quiet-STaR的一个关键挑战是在输入序列的每个token位置高效地生成理由,简单地说,这需要对每个token进行单独的前向传递,这对于长序列来说在计算上是不可行的「A key challenge in Quiet-STaR is efficiently generating rationales at each token position in the input sequence. Naively, this would require a separate forward pass for each token,which becomes computationally intractable for long sequences」
作者首先观察到,语言模型的推理过程会为所有输入token生成下一个token的概率分布,这样就可以实现高度并行的生成We allow for highly parallel generation by first observing that an inference pass of a languagemodel produces a probability distribution over the next tokens for all input tokens.自然地,这使咱们可以从输入中的每个token中采样一个下一个token。如果已经从每个token生成了一个后继token,就无法简单地继续原来的序列
Naturally,this allows us to sample one next token from each token in the input. If one has generated asuccessor from each token, it is not possible to simply continue with the original sequence.
例如,想象一下在“the cat sat”的每个token后预测下一个token,可能会生成“yes orange saw down”——每个后继token本身都是一个合理的下一个token
For example, imagine predicting the next token after each token of “< bos > the cat sat” onemight generate “yes orange saw down” – each successor by itself is a reasonable next token
如下图所示,通过构建一种注意力掩码,使得所有思维token能够关注自身、同一思维中的所有前面思维token以及前面的文本(说白了,就是每个thought token只能看到它之前的thought token以及对应的token文本,这跟GPT在注意力掩码下的解码策略是一致的),从而可以并行生成所有思维的续写。每次推理调用用于为所有文本token生成一个额外的思维token「By constructing an attention mask that allows all thought tokens to pay attention to themselves, all preceding thought tokens with in the same thought,and the preceding text, we can generate continuations of all of the thoughts in parallel. Eachinference call is used to generate one additional thought token for all text tokens.」
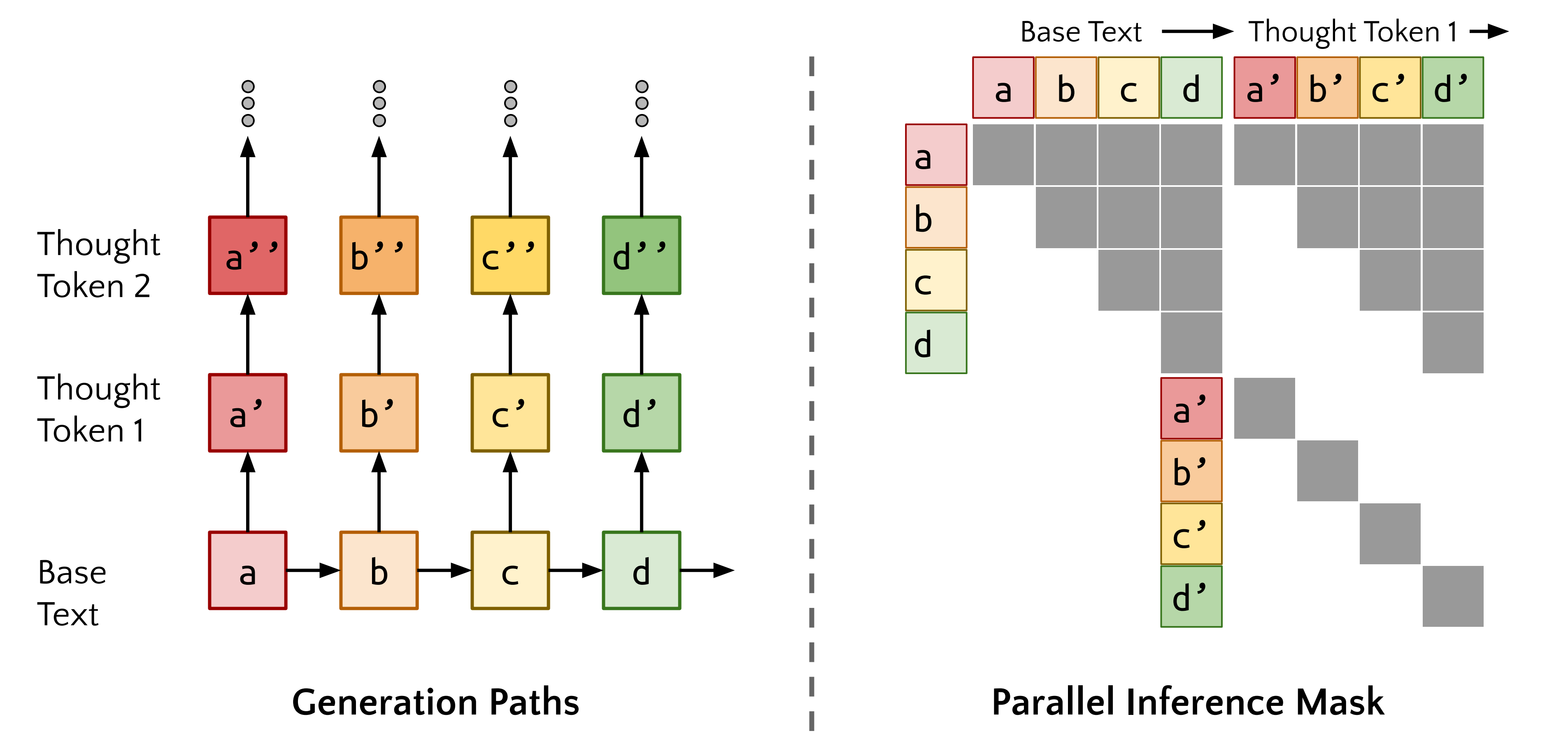
此外,这种并行化的下一个采样token过程可以任意重复多次(或者至少,直到内存耗尽为止)
// 待更
2.2(选读) 如何让模型学会自我纠错——Recursive Introspection(简称RISE,类似STaR)
注,该篇论文的可读性不太高,仅做选读,不影响整体理解
一直以来,让大模型在回答时意识到自己的错误并修正这一点上,并不容易,之前的尝试包括且不限于
prompt模型,要求他们回答时如果错了要及时自我纠正,或者要求模型尝试多次回答,或者在特定领域的问答数据上对模型进行微调但效果都不太好,除非你给模型证明它确实出错了详细证据生成展示多轮连续改进的数据(可能来自高性能模型),但发现仅仅模仿这些数据并不足以实现这种自我纠错的能力
原因在于:首先,来自不同模型的多轮数据不会展示学习者可能犯的错误类型的改进,因此与学习者无关[24]
First, multi-turn data from a different model would not show improvements in the kinds of errors the learner would make, thereby being irrelevant to the learner [24].
其次,通常从专有模型收集的多轮连续数据质量也不高,因为这些模型通常不擅长对自己的错误提出有意义的改进[21],尽管它们仍然可以对手头的问题提供有用的回答
24年7月,来自Carnegie Mellon University、UC Berkeley、3MultiOn的研究者们(Yuxiao Qu, Tianjun Zhang, Naman Garg, Aviral Kumar)提出了一种名为递归自省的方法——RISE 「其对应的论文为Recursive introspection: Teaching language model agents how to self-improve」,类似的工作不少,比如这三个:GLoRE、Generating Sequences by Learning to Self-Correct (该工作发表的比较早,其发表于22年10月底,来自Allen Institute for Artificial Intelligence等机构),以及下一节的SCoRe

RISE的目标是提高大型语言模型在给定问题的连续尝试/回合中的表现
具体来说,给定一个问题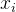 和其标准答案
和其标准答案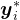 的数据集
的数据集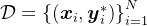 ,他们的目标是获得一个
,他们的目标是获得一个![\operatorname{LLM} \pi_{\theta}\left(\cdot \mid\left[\boldsymbol{x}, \hat{\boldsymbol{y}}_{1: t}, p_{1: t}\right]\right)](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120146173259370642975.png) ,该模型在给定问题
,该模型在给定问题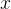 、之前模型对问题的尝试
、之前模型对问题的尝试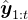 ,以及辅助指令
,以及辅助指令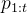 「例如,查找错误并改进回答的指令;或来自环境的额外编译器反馈」时,尽可能正确地解决给定问题
「例如,查找错误并改进回答的指令;或来自环境的额外编译器反馈」时,尽可能正确地解决给定问题
为此,将这一目标编码为以下希望优化的学习目标
![\max _{\pi_{\theta}} \sum_{i=1}^{L} \mathbb{E}_{\boldsymbol{x}, \boldsymbol{y}^{*} \sim \mathcal{D}, \hat{\boldsymbol{y}}_{i} \sim \pi_{\theta}\left(\cdot \mid\left[\boldsymbol{x}, \hat{\boldsymbol{y}}_{1: i-1}, p_{1: i-1}\right]\right)}\left[\mathbb{I}\left(\hat{\boldsymbol{y}}_{i}==\boldsymbol{y}^{*}\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120147173259370761815.png)
与标准的监督微调不同,标准的监督微调训练模型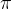 在给定
在给定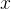 的情况下生成单一的响应
的情况下生成单一的响应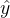 ,而上述方程则训练
,而上述方程则训练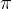 在给定其之前尝试的响应历史
在给定其之前尝试的响应历史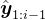 的情况下做出适当反应
的情况下做出适当反应
Unlike standard supervised fine-tuning that trains the model ?to produce a single response ˆ?given ?,Equation 3.1 trains ?to also appropriately react to a given history of responses from its own previousattempts ˆ?1:?−1
如下图所示

将单轮问题转换为多轮马尔可夫决策过程(MDP)
状态由提示prompt、先前尝试的历史记录和来自环境的可选反馈构成
动作是由大型语言模型在当前多轮交互状态下生成的响应右图:数据收集
通过展开当前模型
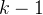 次来收集数据,随后进行响应改进,这种改进通过以下方式获得:
次来收集数据,随后进行响应改进,这种改进通过以下方式获得:(1)自蒸馏:从当前模型中采样多个响应,并使用最佳响应
(2)蒸馏:通过查询更强大的模型获得理想响应
在任一情况下,RISE随后在生成的数据上进行训练
对于上面数据改进的第一种方式——自蒸馏,具体怎么理解呢
具体而言,对于数据集中每个状态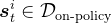 ,从策略中采样
,从策略中采样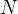 个响应
个响应![\tilde{\boldsymbol{y}}_{t}^{i}[0], \tilde{\boldsymbol{y}}_{t}^{i}[1], \cdots, \tilde{\boldsymbol{y}}_{t}^{i}[N] \sim \pi_{\theta}\left(\cdot \mid \boldsymbol{s}_{t}^{i}\right)](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120149173259370983495.png)
Concretely, for each state in the dataset, ???∈?on-policy, we sample ? responses˜???[0], ˜???[1], · · · , ˜???[?] ∼??(·|???),
并使用这些
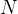 个候选响应中最好的一个(通过关联的奖励值
个候选响应中最好的一个(通过关联的奖励值![\tilde{r}_{t}^{i}[0], \cdots, \tilde{r}_{t}^{i}[N]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120149173259370945688.png) 进行衡量)来重新标记下一步
进行衡量)来重新标记下一步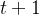 的模型响应,以形成一个改进轨迹
的模型响应,以形成一个改进轨迹and use the best response from these ?candidates (as measured bythe associated reward values ˜???[0], · · · , ˜???[?]) to relabel the model response at the next step ?+ 1 in animprovement trajectory.形式上,假设
![\tilde{\boldsymbol{y}}_{t}^{i}[m]=\arg \max _{j \in[N]} r\left(\boldsymbol{s}_{i}, \tilde{\boldsymbol{y}}_{t}^{i}[j]\right)](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120149173259370935004.png) ,那么在步骤
,那么在步骤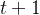 时用改进的响应及其关联的奖励值
时用改进的响应及其关联的奖励值![\tilde{r}_{t}^{i}[m]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120149173259370962735.png) 来标记数据集
来标记数据集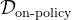 中的响应
中的响应Formally, say ˜???[?] = arg max?∈[?] ?(??, ˜???[?]), then we label the responses in the dataset ?on-policy at step ?+ 1 with the improved response and its associated reward value ˜???[?]:
![\tilde{\mathcal{D}}_{\text {on-policy }+ \text { self-distillation }}:=\left\{\left\{\left(\boldsymbol{s}_{t+1}^{i}, \tilde{\boldsymbol{y}}_{t}^{i}[m], f_{t+1}^{i}, \tilde{r}_{t}^{i}[m]\right)\right\}_{t=0}^{T-1}\right\}_{i=1}^{|\mathcal{D}|}](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120150173259371081006.png)
// 待更
2.3 Self-Correct之SCoRe:通过多轮强化学习进行自我纠正
2.3.1 什么是Self-Correct之SCoRe:对大模型通过RL进行自我纠正 by24年9月
1.1节开头说过,OpenAI o1学会了识别并纠正自己的错误,那它怎么做到的呢
之前对自我纠正LLM的尝试要么依赖于提示工程,要么依赖于专门为自我纠正而微调模型
前者通常无法进行有意义的内在自我纠正而微调方法在推理时需要运行多个模型,例如一个独立的改进模型,或依赖“教师”监督来指导自我纠正的过程使用独立的教师监督模型时,自我纠正不一定优于并行的独立尝试
24年9月下旬,Google开发了一种不需要这些要求的有效自我纠正方法,称为通过强化学习进行自我纠正(Self-Correction via Reinforcement Learning,简称SCoRe),其对应的论文为:《Training Language Models to Self-Correct via Reinforcement Learning》
其仅训练一个模型,该模型既可以对问题产生响应,也可以在没有任何预测反馈的情况下纠正错误简言之,SCoRe是一种多轮次强化学习方法,用于教大型语言模型如何纠正自己的错误且与其最接近的便是上一节介绍的递归自省——Recursive Introspection(简称RISE,类似STaR),他们利用一种类似STaR的迭代方法进行自我纠正。尽管该研究主要使用了预言式教师监督,但其仅通过五轮自我纠正训练获得的初步结果显示出微小的改进,这与在STaR中看到的结果一致Perhaps the closest tous from this set is Qu et al. (2024), which utilizes an iterative STaR-like approach self-correction. Whilethis work largely uses oracle teacher supervision, their preliminary results from training for self-correctiononly show minor improvements over five turns, consistent with the results we see for STaR.
SCoRe采用两阶段训练:
在第一阶段,通过训练纠正第二次尝试的响应,同时将第一次尝试的分布约束在接近基础模型,以产生不易行为崩溃的初始化in the first stage, it produces aninitialization that is less susceptible to behavior collapse by training to correct second-attempt responses while constraining the first-turn distribution to be close to the base model; 然后在第二阶段对两次尝试进行训练以最大化奖励「followed by training on both attempts to maximize reward in the second stage」
关键是,多轮RL的第二阶段采用了一种奖励塑形项,该项奖励的是“朝向自我纠正的进展”,而不是最终响应的正确性
the second stage of multi-turn RL employs are ward shaping term that rewards “progress” towards self-correction as opposed to the correctness of the final response
在效果上,相对于基础的Gemini模型,SCoRe的方法在MATH(Hendrycks等人,2021)的推理问题上实现了绝对15.6%的自我纠正提升,并且实现了绝对9.1%的提升
具体来说,如下图所示,表示的是自我纠正的问题设定「SCoRe不仅训练模型生成最佳可能的响应,还旨在训练模型在最后一次尝试中生成最佳最终响应。在第二轮中,可能会以指令的形式提供额外输入,要求模型自我纠正或由模型生成」
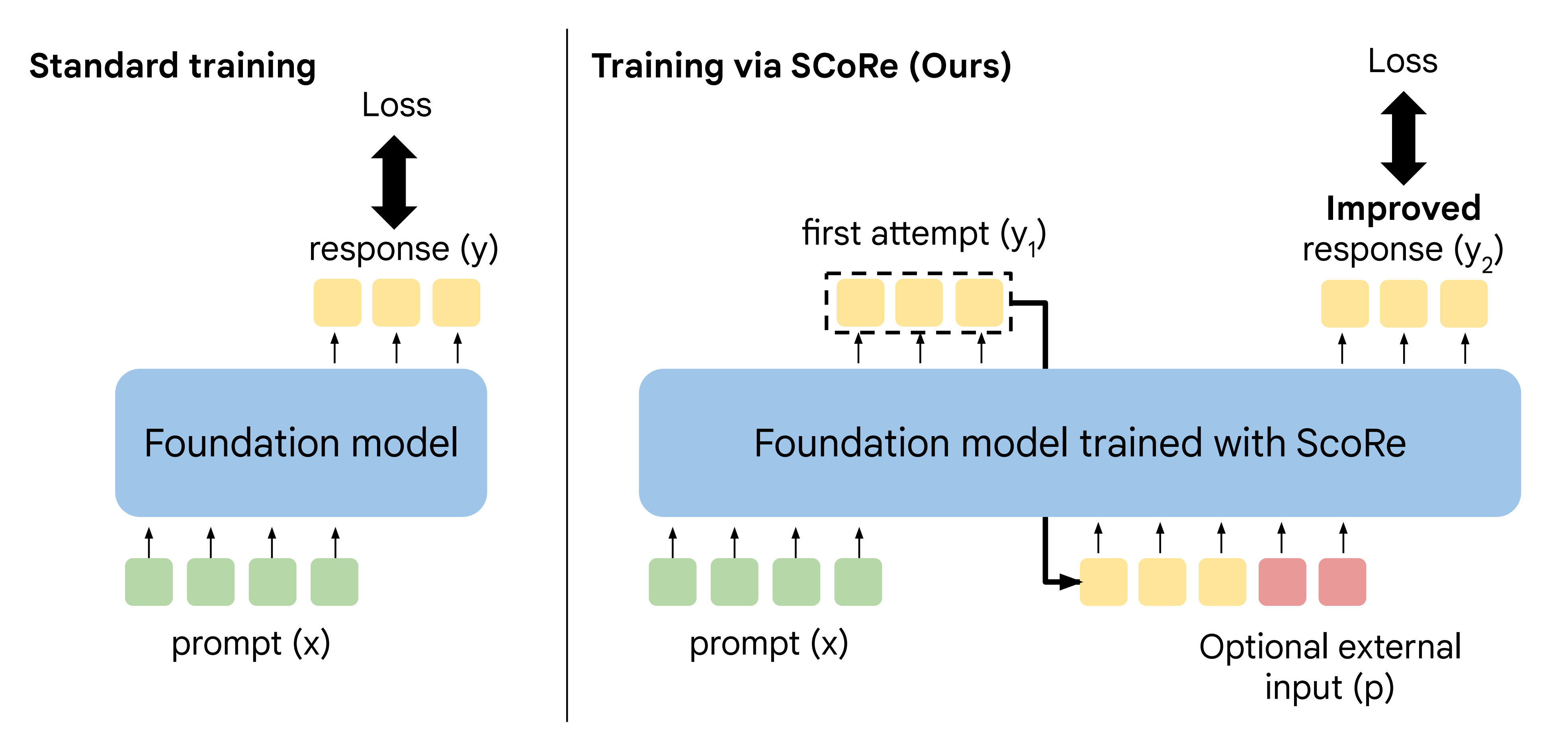
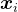 和响应
和响应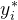 的数据集
的数据集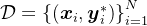 然后训练一个LLM策略
然后训练一个LLM策略![\pi_{\theta}\left(\cdot \mid\left[x, \hat{y}_{1: l}, p_{1: l}\right]\right)](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120151173259371126404.png) ,该策略在给定问题
,该策略在给定问题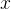 、之前模型对该问题的
、之前模型对该问题的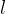 次尝试
次尝试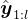 以及辅助指令
以及辅助指令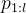 「例如,寻找错误并改进响应的指令」的情况下,尽可能正确地解决问题
「例如,寻找错误并改进响应的指令」的情况下,尽可能正确地解决问题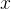
这种形式化类似于Qu等人「即上面提过的RISE,详见Recursive introspection: Teaching language model agents how to self-improve」中的多轮MDP作者还假设可以访问一个oracle奖励̂
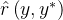 ,例如一个答案检查器「即answer checker,详见此论文:Solving math word problems with process-and outcome-based feedback,即要求语言模型生成推理步骤可以提高许多推理任务的性能,且对于正确的推理步骤,发现有必要使用基于过程的监督或来自模拟基于过程的反馈的学习奖励模型的监督」,通过将响应
,例如一个答案检查器「即answer checker,详见此论文:Solving math word problems with process-and outcome-based feedback,即要求语言模型生成推理步骤可以提高许多推理任务的性能,且对于正确的推理步骤,发现有必要使用基于过程的监督或来自模拟基于过程的反馈的学习奖励模型的监督」,通过将响应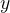 与oracle响应
与oracle响应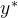 进行比较来评估其正确性
进行比较来评估其正确性We also assumeaccess to an oracle reward ̂?(?, ?∗), such as an answer checker (Uesato et al., 2022), that evaluates the correctness of response ? by comparing it with the oracle response ?∗. C
至关重要的是,不假设在测试时能访问这个oracle;相反,模型必须推断是否存在错误,并在必要时进行纠正,这在——例如数学推理问题中经常发生
接下来,需要找到一个LLM策略 ,将输入token
,将输入token  映射到输出标记□,以最大化在
映射到输出标记□,以最大化在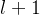 轮(
轮(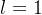 )结束时从验证器verifier获得的正确性奖励
)结束时从验证器verifier获得的正确性奖励
![\max _{\pi_{\theta}} \mathcal{E}_{\boldsymbol{x}, \boldsymbol{y}^{*} \sim \mathcal{D}, \hat{\boldsymbol{y}}_{l+1} \sim \pi_{\theta}\left(\cdot \mid\left[x, \hat{y}_{1: l}, p_{1: l}\right]\right)}\left[\sum_{i=1}^{l+1} \hat{r}\left(\hat{\boldsymbol{y}}_{i}, \boldsymbol{y}^{*}\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120153173259371310343.png)
请注意,与标准的监督微调或常见的强化学习微调流程不同——这些流程训练策略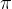 直接生成
直接生成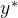 「或任何其他
「或任何其他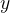 使得
使得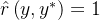 」
」
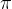 ,其中中间步骤是间接监督的,以最大化总和「Equation 1 trains ? over multiple attempts simultaneously, where intermediate turns are supervised indirectly to maximize the sum」
,其中中间步骤是间接监督的,以最大化总和「Equation 1 trains ? over multiple attempts simultaneously, where intermediate turns are supervised indirectly to maximize the sum」然后使用基础强化学习微调方法,采用了一种带有固定模型KL散度惩罚的REINFORCE策略梯度训练方法「Back to Basics: Revisiting REINFORCE Style Optimization for Learning from Human Feedback in LLMs」,这种方法广泛应用于大语言模型的强化学习微调中,主要用于单轮RLHF的场景形式上,这些方法训练策略
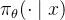 以优化以下内容,其中
以优化以下内容,其中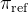 是一个参考策略
是一个参考策略 ![\max _{\theta} \mathbb{E}_{\boldsymbol{x}_{t}, \boldsymbol{y}_{t} \sim \pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{t}\right)}\left[\hat{r}\left(\boldsymbol{y}_{t}, \boldsymbol{y}^{*}\right)-\beta_{1} D_{K L}\left(\pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{t}\right)| | \pi_{\mathrm{ref}}\left(\cdot \mid \boldsymbol{x}_{t}\right)\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120154173259371432357.png)
2.3.2 SCoRe:通过多轮强化学习进行自我纠正 by24年9月
为了衡量自我纠正性能(本文中考虑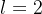 ),然后报告并分析以下指标:
),然后报告并分析以下指标:
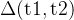 :第一次和第二次尝试之间模型准确率的净提升,衡量自我纠正的效果
:第一次和第二次尝试之间模型准确率的净提升,衡量自我纠正的效果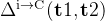 :在第一次尝试中错误但在第二次尝试中变为正确的问题的比例,衡量自我纠正能解决多少新问题
:在第一次尝试中错误但在第二次尝试中变为正确的问题的比例,衡量自我纠正能解决多少新问题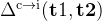 :在第一次尝试中正确但在第二次尝试中变为错误的问题的比例,衡量模型对正确答案理解的程度
:在第一次尝试中正确但在第二次尝试中变为错误的问题的比例,衡量模型对正确答案理解的程度 在对训练数据进行强化学习策略优化时,至少有两种同样好的解决方案:
(i) 学习如何从第一次尝试到第二次尝试进行改进或 (ii)学习如何在第一次尝试时就产生最佳响应,然后在第二次尝试中不进行修正虽然一个好的自我纠正策略应该最大化 accuracy@t1 和 accuracy@t2,但作者发现标准的强化学习会导致行为不再纠正——言外之意,就是标准的RL不符合作者的预期
因此,作者在 SCoRe 中的关键见解是必须更明确地鼓励自我纠正行为,这通过一个两阶段的方法来实现
第一阶段(Stage I)起到初始化的作用,在这一阶段,我们通过优化第二次尝试的准确率,同时明确地将第一次尝试的分布限制在基础模型上,来训练模型以实现两次尝试行为的解耦The first stage (Stage I) serves the role of initialization where we train the model to decouple its behavior across the two attempts by attempting to optimize second-attemptaccuracy while explicitly constraining the distribution of first attempts to the base model.接下来,阶段 II 共同优化两次尝试的奖励。为了确保阶段 II 不会退化为“直接”解决方案,作者对奖励进行偏向,以加强自我纠正的进展
From here,Stage II then jointly optimizes the reward of both attempts. To ensure that Stage II does not collapse to the “direct” solution, we bias the reward to reinforce self-correction progress
具体而言,如下图所示
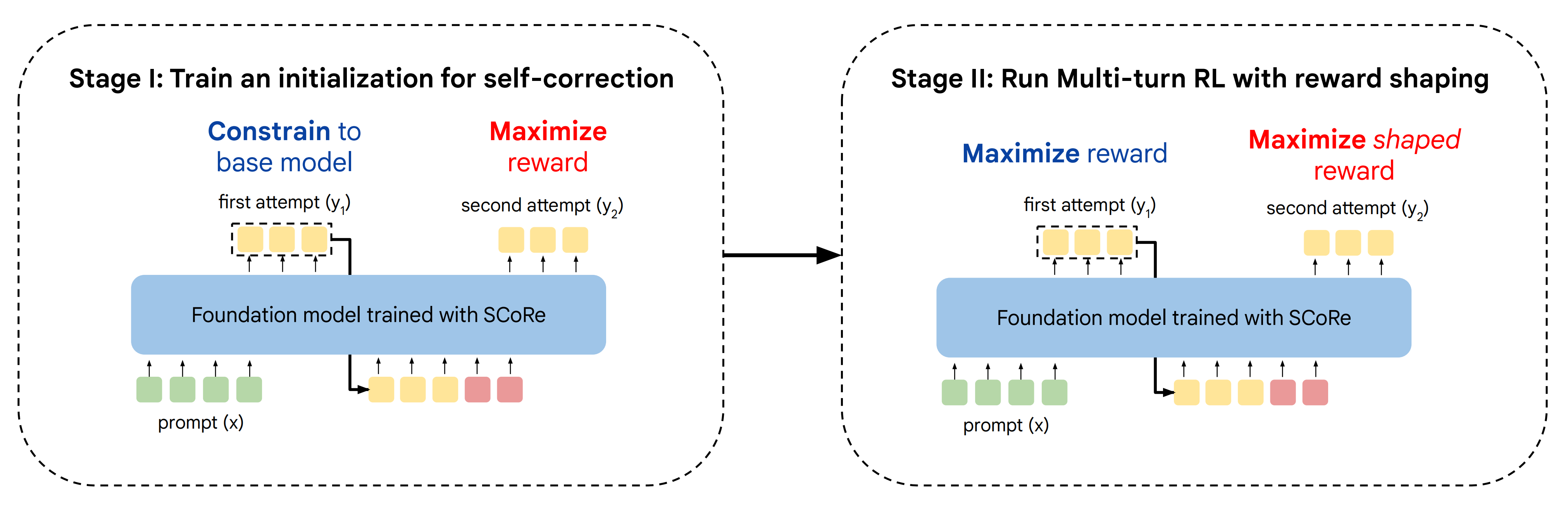
SCoRe的第一阶段目标是通过改进基础模型在第二次尝试上的覆盖率来获得一个初始化,而这种改进是基于第一次尝试的结果,以减少后续的自我纠错训练中出现行为坍塌的可能性
The goal of Stage I of SCoRe is to obtain an initialization by improving the base model’s coverage over second attempts given the first attempt, so that subsequent training for self-correction is less prone tobehavior collapse.
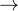 虽然这通常通过SFT来完成,但由于SFT本身也存在崩溃。因此,作者在这一阶段使用强化学习来解耦两次尝试
虽然这通常通过SFT来完成,但由于SFT本身也存在崩溃。因此,作者在这一阶段使用强化学习来解耦两次尝试为此,作者明确地微调基础模型,使其在第二次尝试时产生高奖励的响应,同时通过使用KL散度约束模型,使其第一次尝试保持接近基础模型,从而不改变第一次尝试
To do so,we explicitly fine-tune the base model to produce high-reward responses at the second attempt, whileforcing the model to not change its first attempt by constraining it to be close to the base model usinga KL-divergence
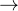 且尽管这看起来可能次优——减少第一次尝试中的错误本应带来更好的第二次尝试——但正如作者将展示的,这个阶段在减少基础模型仅仅将第一次和第二次尝试的分布简单地耦合在一起的偏见方面是至关重要的,从而在实际进行多轮RL时避免行为坍塌
且尽管这看起来可能次优——减少第一次尝试中的错误本应带来更好的第二次尝试——但正如作者将展示的,这个阶段在减少基础模型仅仅将第一次和第二次尝试的分布简单地耦合在一起的偏见方面是至关重要的,从而在实际进行多轮RL时避免行为坍塌While this may appear sub-optimal – a first attempt with fewer mistakes should leadto a better second attempt – but as we will show, this stage is critical in reducing the base model’s biastowards simply coupling the first and second-attempt distributions, thus avoiding behavior collapse when actual multi-turn RL is run
其目标为
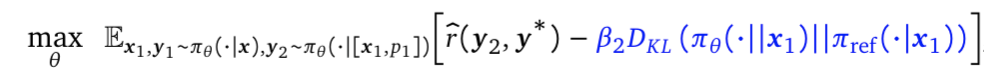
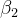 是一个超参数,旨在仅在第一次尝试时强制执行严格的KL惩罚,以避免第一次对话的response发生偏移(如上标蓝的部分所示)
是一个超参数,旨在仅在第一次尝试时强制执行严格的KL惩罚,以避免第一次对话的response发生偏移(如上标蓝的部分所示)有两个小问题需要注意一下
1) 首先是为何用KL惩罚,其实很好理解,就是让迭代中的策略
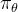 不要跟最初的策略
不要跟最初的策略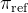 相差太远,类似ChatGPT的迭代——详见此文ChatGPT原理的「3.1.3 InstructGPT训练阶段3:如何通过PPO算法进一步优化模型的策略」
相差太远,类似ChatGPT的迭代——详见此文ChatGPT原理的「3.1.3 InstructGPT训练阶段3:如何通过PPO算法进一步优化模型的策略」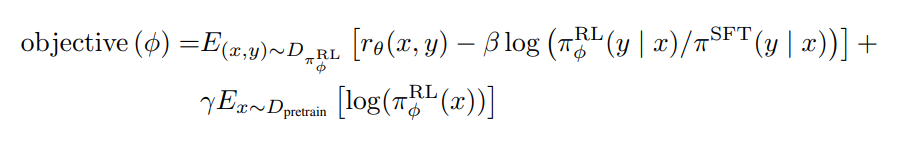
2) 此处仍然使用来自上节最后的默认KL散度惩罚——即如下所示
![\max _{\theta} \mathbb{E}_{\boldsymbol{x}_{t}, \boldsymbol{y}_{t} \sim \pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{t}\right)}\left[\hat{r}\left(\boldsymbol{y}_{t}, \boldsymbol{y}^{*}\right)-\beta_{1} D_{K L}\left(\pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{t}\right)| | \pi_{\mathrm{ref}}\left(\cdot \mid \boldsymbol{x}_{t}\right)\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120157173259371714884.png)
但权重相对较小,并且为了清晰起见在上述方程中省略
且实验证明与标准多轮强化学习相比,本阶段I在分离两个响应方面更为有效,并且导致了更好的阶段II性能阶段二:带奖励塑造的多轮次强化学习,相当于第二轮鼓励大胆尝试,并试图纠正
SCoRe的第二阶段从第一阶段初始化,现在共同优化两次尝试的性能
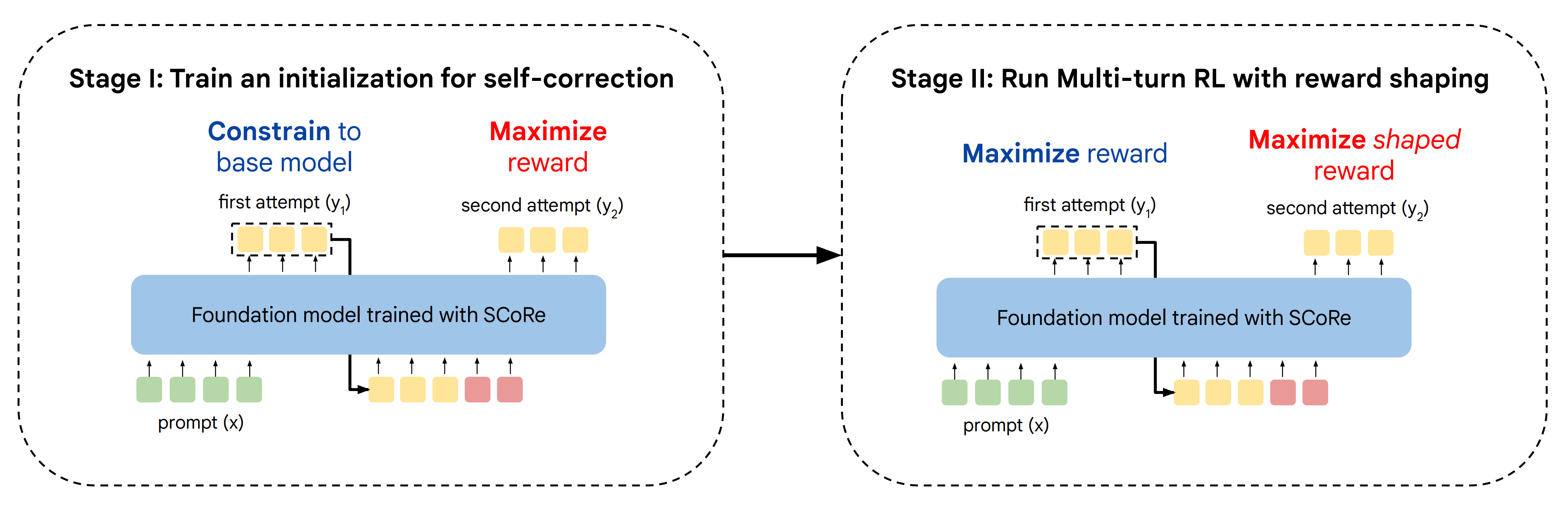
 ,定义为方程4
,定义为方程4![\max _{\theta} \mathbb{E}_{\boldsymbol{x}_{1}, \boldsymbol{y}_{1} \sim \pi_{\theta}(\cdot \mid \boldsymbol{x}), \boldsymbol{y}_{2} \sim \pi_{\theta}\left(\cdot \mid\left[\boldsymbol{x}_{1}, p_{1}\right]\right)}\left[\sum_{i=1}^{2} \hat{r}\left(\boldsymbol{y}_{i}, \boldsymbol{y}^{*}\right)-\beta_{1} D_{K L}\left(\pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{i}\right)| | \pi_{\mathrm{ref}}\left(\cdot \mid \boldsymbol{x}_{i}\right)\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120157173259371771744.png)
其中
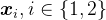 对应于作为上下文传递给模型的输入token集
对应于作为上下文传递给模型的输入token集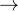 为了防止学习过程在阶段II中崩溃为非自我纠正的解决方案,需要将学习问题偏向于自我纠正
为了防止学习过程在阶段II中崩溃为非自我纠正的解决方案,需要将学习问题偏向于自我纠正To prevent the learning process from collapsing to a non self-correcting solution in Stage II,we need to bias the learning problem towards self-correction」
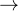 作者通过奖励塑造来实现这一点:通过奖励那些在学习期望的自我纠正行为上取得“进展”的转换
作者通过奖励塑造来实现这一点:通过奖励那些在学习期望的自我纠正行为上取得“进展”的转换We implement this via reward shaping:by rewarding transitions that make “progress” towards learning the desired self-correction behavior.
具体来说,给定从策略中采样的一个两轮回合
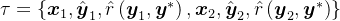
作者在方程4中
![\max _{\theta} \mathbb{E}_{\boldsymbol{x}_{1}, \boldsymbol{y}_{1} \sim \pi_{\theta}(\cdot \mid \boldsymbol{x}), \boldsymbol{y}_{2} \sim \pi_{\theta}\left(\cdot \mid\left[\boldsymbol{x}_{1}, p_{1}\right]\right)}\left[\sum_{i=1}^{2} \hat{r}\left(\boldsymbol{y}_{i}, \boldsymbol{y}^{*}\right)-\beta_{1} D_{K L}\left(\pi_{\theta}\left(\cdot \mid \boldsymbol{x}_{i}\right)| | \pi_{\mathrm{ref}}\left(\cdot \mid \boldsymbol{x}_{i}\right)\right)\right]](http://m.zhangshiyu.com/zb_users/upload/2024/11/20241126120158173259371810048.png)
的第二次尝试中修改奖励̂
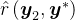 ,加入一个奖励
,加入一个奖励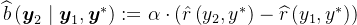
其中
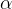 是一个理想情况下大于1.0的正常数乘数
是一个理想情况下大于1.0的正常数乘数在第二次尝试中加入这个额外奖励,通过仅强调那些改变响应正确性的转换来衡量进步的概念,并在第二次尝试中将正确响应变为不正确的转换上施加重负的惩罚
Adding thisbonus to the second attempt measures a notion of progress by only emphasizing transitions that flip thecorrectness of the response and assigns a heavy negative penalty to transitions that change a correctresponse to incorrect in the second attempt.
相当于如果第二次尝试与第一次尝试相比提高了正确性,则会在第二次尝试的奖励中添加奖励,而如果响应降低,则会施加惩罚
因此,加入这个额外奖励应该能够规范训练过程,使其不会崩溃到那个在训练集上看起来也是最优的“直接”解决方案上,而是学习自我纠正
Thus, the addition of this bonus should regularize thetraining process from collapsing on to the “direct” solution that also appears optimal on the training setbut does not learn self-correction.
这意味着模型被鼓励去探索和尝试不同的响应,即使这些尝试可能不是立即正确的,但它们有助于模型学习如何在后续的尝试中进行自我纠正和改进
且可以避免模型过早地收敛到一个固定的、可能无法适应新情况的解决方案上,而是鼓励模型发展出更加灵活和适应性强的策略
事实上,这篇论文的可读性也一般,我在Reddit看到了关于这篇论文的讨论:谷歌发布新论文:通过强化学习训练语言模型进行自我纠正,有兴趣的可以看看
第三部分 对AlphaZero技术的借鉴:Self-play RL、MCST
3.1 如何进一步加强推理能力:延长思考时间而非单纯增加模型参数
24年8月份,来自UC Berkeley、Google DeepMind的研究者发布的此篇论文《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters》证明在加强模型的推理能力方面,延长思考时间比单纯增加模型参数更有效》
毕竟人类在面对相对复杂的问题时,也会花更长时间思考,以从长计议
3.1.1 如何最优地扩展测试时的计算
// 待更
3.1.2 训练易于搜索的验证器及针对PRM的搜索方法(Best-of-N、Beam Search、Lookahead Search)
论文中提到,他们首先训练易于搜索的验证器
在PRM训练的问题上,最初,PRM训练[22,42]使用了人类众包工人的标签。虽然Lightman等人[22]发布了他们的PRM训练数据(即PRM800k数据集),但作者发现这些数据在很大程度上对我们无效
他们发现,即使是最简单的策略,例如最佳N取样,也很容易利用在该数据集上训练的PRM。作者假设这可能是由于他们数据集中GPT-4生成样本与作者PaLM 2模型之间的分布偏移所致「We found that it was easy to exploit a PRM trained on this dataset via even naïve strategies such as best-of-N sampling. We hypothesize that this is likely a result of the distribution shift between the GPT-4 generated samples in their dataset and our PaLM 2 models」总之,最终作者没有进行昂贵的过程来为他们Google的PaLM 2模型收集众包工人的PRM标签,而是采用了Wang等人[45]的的方法,在没有人工标注的情况下监督PRMs,使用通过从解决方案的每一步进行蒙特卡罗展开获得的每步正确性估计(we instead apply the approach of Wang et al. [45] to supervise PRMs without human labels, using estimates of per-step correctness obtained from running Monte Carlo rollouts from each step in the solution)因此,作者的PRM的每步预测对应于基础模型采样策略的未来奖励的估计(Our PRM’s per-step predictions there fore correspond to value estimates of reward-to-go for the base model’ssampling policy)其类似于最近的工作[31,45],且他们还与ORM基线进行了比较,但发现我们的PRM始终优于ORM
因此,本节中的所有搜索实验均使用PRM模型。关于PRM训练的更多细节见附录D
其次在答案聚合问题上,他们在测试时,可以使用基于过程的验证器对从基础模型中采样的一组解决方案中的每个步骤进行评分(At test time, process-based verifiers can be used to score each individual step in aset of solutions sampled from the base model)
为了使用PRM选择最佳N个答案,需要一个函数来聚合每个答案的每个步骤得分,以确定正确答案的最佳候选者
为此,作者首先聚合每个答案的每个步骤得分,以获得完整答案的最终得分(逐步聚合)。然后,在答案之间进行聚合以确定最佳答案(答案间聚合)
具体来说,如下处理逐步和答案间聚合
逐步聚合与其通过取乘积或最小值[22,45]来聚合每步得分,作者更倾向于使用PRM在最后一步的预测作为完整答案的得分
Rather than aggregating the per-step scores by taking the product orminimum [22, 45], we instead use the PRM’s prediction at the last step as the full-answer score.
因为,作者发现这在他们研究的所有聚合方法中表现最好(见附录E)答案间聚合
作者遵循Li等人的方法[21],应用“最佳N加权”选择而非标准的最佳N
最佳N加权选择在所有具有相同最终答案的解决方案中边缘化验证者的正确性分数,选择总和最大的最终答案
Best-of-N weighted selection marginalizes the verifier’s correctness scoresacross all solutions with the same final answer, selecting final answer with the greatest total sum
其次,在测试时通过搜索方法优化PRM
作者研究了三种搜索方法,这些方法从少样本提示的基础LLM中采样输出,下图展示了一个示例

第一,加权最佳-N:Best-of-N,从 N 个样本中选择最佳答案,并根据 PRM 最终得分选择最佳答案,如上图左侧所示
从基础LLM中独立采样N个答案,然后根据PRM的最终答案判断选择最佳答案
第二,束搜索:Beam Search,束搜索在每一步采样 N 个候选项,并根据 PRM 选择前 M 个继续搜索,如上图中部所示
束搜索通过搜索每一步的预测来优化PRM。他们的实现与BFS-V [10,48]相似
具体来说,作者考虑一个固定数量的束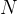 (比如上图是4)和一个束宽度
(比如上图是4)和一个束宽度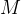 (比如上图是2),然后运行以下步骤:
(比如上图是2),然后运行以下步骤:
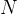 个初始预测根据PRM预测的逐步奖励估算对生成的步骤进行评分(在此设置中,由于奖励是稀疏的,这也对应于前缀的总奖励仅筛选出前
个初始预测根据PRM预测的逐步奖励估算对生成的步骤进行评分(在此设置中,由于奖励是稀疏的,这也对应于前缀的总奖励仅筛选出前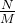 得分最高的步骤(如上图中间部分所示,筛选出第一行的第2个、第4个)现在从每个候选者中,从下一步中采样
得分最高的步骤(如上图中间部分所示,筛选出第一行的第2个、第4个)现在从每个候选者中,从下一步中采样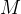 个提案,结果再次得到总计
个提案,结果再次得到总计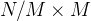 个候选前缀(如上图中间部分所示,筛选出第二行的第1个、第4个,相当于在前两行中,有两束候选,一个是2-1,一个是4-4)
个候选前缀(如上图中间部分所示,筛选出第二行的第1个、第4个,相当于在前两行中,有两束候选,一个是2-1,一个是4-4)然后再次重复步骤2-4(在第三行时,最佳的两束候选是2-1-1,4-4-4,在第四行时,最佳的唯一一束候选是4-4-3-3)
通过运行此算法,直到找到一个解决方案或达到最大光束扩展轮数(在作者的情况下为40)。他们以N个最终答案候选结束搜索,并对其应用上述的最佳N加权选择来进行最终答案预测
第三,前瞻搜索:Lookahead Search,前瞻搜索将束搜索的每一步扩展为利用 k 步前瞻,同时评估要保留和继续搜索的步骤,如下图右侧所示
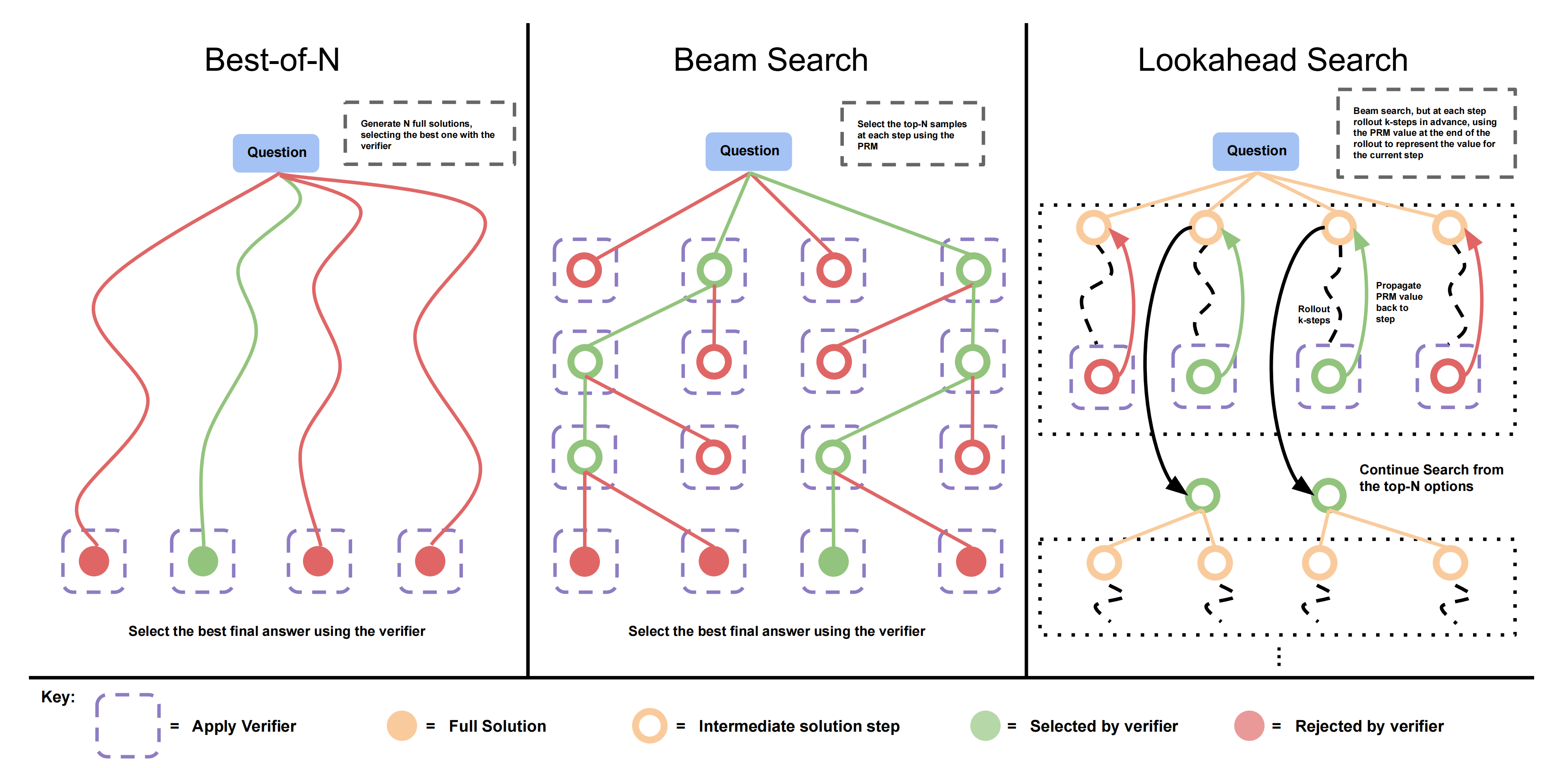
前瞻搜索修改了束搜索评估单个步骤的方式,它使用前瞻展开来提高每一步搜索过程中的PRM值估计的准确性
具体来说,在束搜索的每一步中,前瞻搜索不是使用当前步骤的PRM得分来选择TOP候选,而是进行模拟,展开到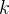 步,若达到解的终点则提前停止
步,若达到解的终点则提前停止at each step in the beam search, rather than using the PRM score at the current step to select the top candidates, lookahead search performs a simulation, rolling out up to ?steps furtherwhile stopping early if the end of solution is reached.为了最小化模拟展开中的方差,使用温度0进行展开。在此展开结束时PRM的预测用于为束搜索的当前步骤评分。换句话说,可以将束搜索视为
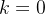 时前瞻搜索的一种特殊情况
时前瞻搜索的一种特殊情况给定一个准确的PRM,增加
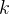 应该能在每步值估计的准确性上有所提升,当然,有得必有失,此举必然需要额外的计算还需注意,这种版本的前瞻搜索是MCTS [38]的一种特殊情况,其中MCTS中设计用于促进探索的随机元素被移除,因为PRM已经训练完成且被冻结
应该能在每步值估计的准确性上有所提升,当然,有得必有失,此举必然需要额外的计算还需注意,这种版本的前瞻搜索是MCTS [38]的一种特殊情况,其中MCTS中设计用于促进探索的随机元素被移除,因为PRM已经训练完成且被冻结Also note that this version of lookahead search is a special case of MCTS [38], where in the stochastic elements of MCTS, designed to facilitate exploration, are removed since the PRM is already trained and is frozen.
这些随机元素在学习值函数时非常有用(毕竟已经通过PRM学习了),但在想要利用而非探索的测试时刻则不太有用
These stochastic elements are largely useful for learning the value function (which we’ve already learned with our PRM),but less useful at test-time when we want to exploit rather than explore.
因此,前瞻搜索在很大程度上代表了MCTS风格方法在测试时的应用方式(Therefore, lookahead search islargely representative of how MCTS-style methods would be applied at test-time.)
3.2 如何让模型更高效的搜索可行性方案
2024年9月,《Planning In Natural Language Improves LLM Search For Code Generation》:这篇论文提出了PLANSEARCH算法,用于解决LLMs在推理时缺乏多样性导致搜索效率低下的问题
该算法通过生成多样化的观察,组合观察形成候选计划,并实现代码,从而在想法空间中增加多样性,显著提高了代码生成的性能
// 待更
3.3 AlphaZero
《Monte Carlo Tree Search Boosts Reasoning via Iterative Preference Learning》
《ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search》
AlphaZero论文为《Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm》
《Alphazero-like Tree-Search can Guide Large Language Model Decoding and Training》
// 待更
第四部分 从UCL、上交的复现工作探究小团队如何快速复现o1
// 待更
本文的修订完善记录
本文自10.12发布以来,一直在不断更新,12 13 14这三天没来得及记录,以下是从10.15日起的修订记录
10.15,反复修订此节——2.1.2 Quiet-STaR: 语言模型可以教会自己在说话前思考特别是逐行解读其伪代码10.16,反复修订以下这两节的内容
2.2(选读) 如何让模型学会自我纠错——Recursive Introspection(简称RISE,类似STaR)
2.3 Self-Correct之SCoRe:通过多轮强化学习进行自我纠正10.19,重新梳理全文结构(全文目录亦有调整),比如新增一节:1.2 如何让模型学会分解问题10.22,编写下面这几节
3.1.2 训练易于搜索的验证器及针对PRM的搜索方法(Best-of-N、Beam Search、Lookahead Search)..