个人主页:喜欢做梦
欢迎 ? 关注 ✨ 点赞 ? 收藏 ? 评论!!!
目录
1.相同的树
2.另一棵树的子树
3.翻转二叉树
4.平衡二叉树
5.对称二叉树
1.相同的树
题目:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例:

思路:判断结构和值是否相同
结构可能出现的三种情况: 节点都为null,该情况结构相同;p的节点为null,q的节点不为null;或者q的节点为null,p的节点不为null,该情况结构不同;节点都不为null,说明结构相同 ,随后判断值是否相同; 那么值是否相同:不相同返回;看其左右子树是否相同 public boolean isSameTree(TreeNode p, TreeNode q) { //结构是否相同: //结构可能出现的三种情况: //1.节点都为null if(p==null && q==null){ return true; } //2.p的节点为null,q的节点不为null;或者q的节点为null,p的节点不为null if(p==null && q!=null ||q==null && p!=null ){ return false; } //前两种结构已经判断,剩下最后一种就是都不为空,如果都不为空,说明结构相同 //那我们要判断值相不相同 if(p.val!=q.val){ return false; } //判断左右子树 return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right); }2.另一棵树的子树
题目:
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例:
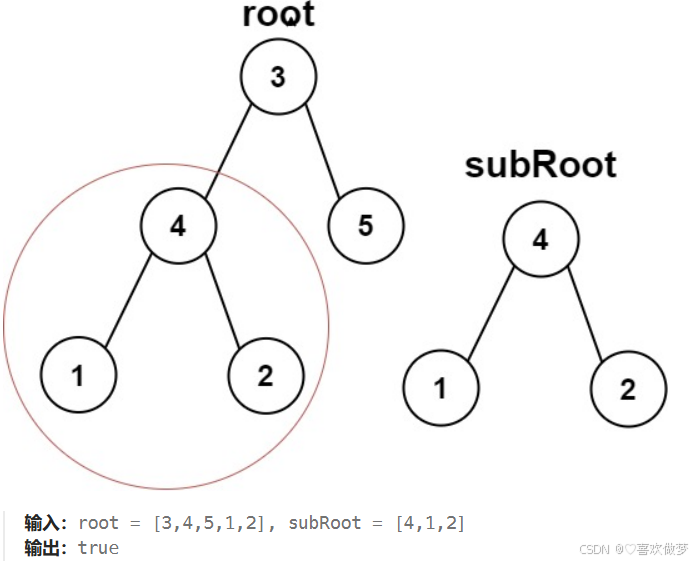
思路:
判断是不是根的子树;判断是不是左子树的子树或者子树的子树;判断是不是右子树的子树或者子树的子树; 总之:判断与根、左、右子树是不是相同的树;上面那道题,我们已经写过判断相同的树的代码,直接使用就好了;
public boolean isSameTree(TreeNode p, TreeNode q) { //结构是否相同: //结构可能出现的三种情况: //1.节点都为null if(p==null && q==null){ return true; } //2.p的节点为null,q的节点不为null;或者q的节点为null,p的节点不为null if(p==null && q!=null ||q==null && p!=null ){ return false; } //前两种结构已经判断,剩下最后一种就是都不为空,如果都不为空,说明结构相同 //那我们要判断值相不相同 if(p.val!=q.val){ return false; } return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right); } //另一棵子树的子树: //1.判断是不是根的子树; //2.判断是不是左子树的子树; //3.判断是不是右子树的子树; //总之:判断与根、左、右子树是不是相同的树 public boolean isSubtree(TreeNode root, TreeNode subRoot) { //首先判断节点是不是为null if(root==null){ return false; } //1.判断是不是根的子树; if(isSameTree(root,subRoot)){ return true; } //2.判断是不是左子树的子树; if(isSubtree(root.left,subRoot)){ return true; } //3.判断是不是右子树的子树; if(isSubtree(root.right,subRoot)){ return true; } return false; }3.翻转二叉树
题目:给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例:
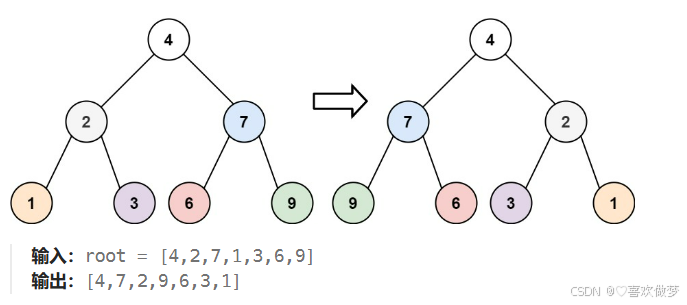
思路:
判断有无节点;将左右子树进行交换;递归左右子树的子树进行交换。 //翻转二叉树:就是将左右子树进行翻转 public TreeNode invertTree(TreeNode root) { if(root==null){ return null; } //将左右子树进行交换 TreeNode tmp=root.left; root.left=root.right; root.right=tmp; //递归左右子树 invertTree(root.left); invertTree(root.right); return root; }4.平衡二叉树
题目 :给定一个二叉树,判断它是否是 平衡二叉树
平衡二叉树 是指该树所有节点的左右子树的高度相差不超过 1。
示例:
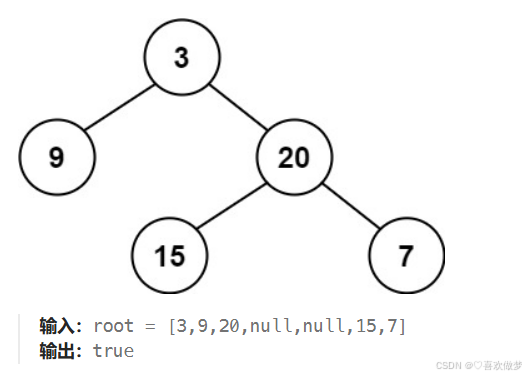
思路:
判断有无根节点,有则返回true;算出左右子树的高度;左右子树的高度相差的绝对值是否小于等于1。(高度就是取左右子树的最大值)//判断平衡二叉树: public boolean isBalanced(TreeNode root) { //判断有无根节点 if(root==null){ return true; } // 算出左右子树的高度; int leftheight=height(root.left); int rightheight=height(root.right); //左右子树的高度相差的绝对值是否小于等于1。 return Math.abs(leftheight-rightheight)<=1 &&isBalanced(root.left)&& isBalanced((root.right)); } //获取高度:取左子树和右子树中的最大高度 public int height(TreeNode root){ if(root==null){ return 0; } int leftHeight=height(root.left); int rightHeight=height(root.right); return Math.max(leftHeight,rightHeight)+1; }5.对称二叉树
题目:给你一个二叉树的根节点 root , 检查它是否轴对称。
示例:
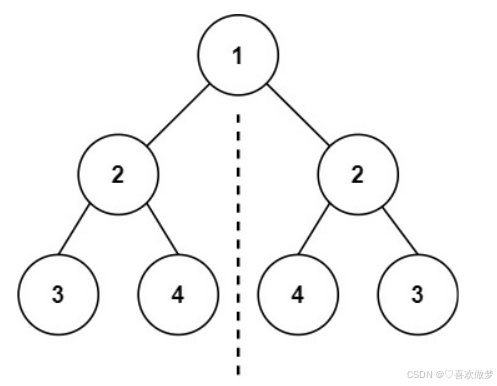
思路:
判断有无根节点,如果没有那么也是轴对称图形;判断左右子树是否对称(与判断相同的树原理相同,只是对象不一样): 判断结构;判断值;递归右子树的左子树与左子树的右子树是否相同以及左子树的左子树与右子树的右子树是否相同; public boolean isSymmetric(TreeNode root) { //判断有无根节点,如果没有那么也是轴对称图形; if(root==null){ return true; } //判断左右子树是否对称, return isSymmetricChild(root.left,root.right); } //判断左右子树是否对称:(原理同判断是否是一棵相同的树同理) //判断结构是否相同 //值是否相同 public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree) { //左右节点都为null if(leftTree==null && rightTree==null){ return true; } //左节点为null,右节点不为null;右节点为null,左节点不为null if(leftTree==null && rightTree!=null||leftTree!=null && rightTree==null){ return false; } //都不为null,判断值是否相同 if(leftTree.val!=rightTree.val){ return false; } return isSymmetricChild(leftTree.left,rightTree.right) && isSymmetricChild(leftTree.right,rightTree.left); }
今日的题目就到这里啦,下期再来!!!
