
公主请阅
容器适配器容器适配器的特点 栈和队列的模拟实现deque的介绍1. 内存开销较高2.随机访问性能略低于 vector3. 与指针或迭代器的兼容性r4. 不适合用于需要频繁中间插入和删除的场景5. 在特定平台上的实现不一致6. 缺乏shrink_to_fit支持总结 题目 priority_queue 优先级队列使用最小优先队列使用场景 priority_queue的模拟实现 仿函数的介绍仿函数的基本概念仿函数的基本用法仿函数的优点常见的仿函数应用示例:在STL中使用仿函数总结 题目155.最小栈JZ31 栈的压入、弹出序列150. 逆波兰表达式求值232. 用栈实现队列225. 用队列实现栈
容器适配器
容器适配器(Container Adapter)是C++标准模板库(STL)中的一种设计模式,专门用于提供一种经过简化和限制的接口,使得不同的容器类型可以表现出类似的行为。容器适配器不会创建新的容器,而是基于已有的容器(如 deque、vector 等)进行包装,以改变或限制其接口,从而提供不同的行为和使用方式。
STL 中常见的容器适配器有以下三种:
栈(Stack)使用 std::stack 类实现。
默认底层容器为 std::deque,也可以用 std::vector 或 std::list 替换。
栈是“后进先出” (LIFO) 数据结构,适配器屏蔽了底层容器的大部分接口,提供 push、pop 和 top 操作。
使用 std::queue 类实现。
默认底层容器为 std::deque,也可以使用其他序列容器(如 std::list)。
队列是“先进先出” (FIFO) 数据结构,适配器仅保留 push、pop 和 front、back 等接口。
使用 std::priority_queue 类实现。
默认底层容器为 std::vector,底层使用堆结构进行元素排序。
优先级队列允许快速访问和移除最高优先级的元素。适配器提供 push、pop 和 top 操作,自动按照优先级排序。
容器适配器的特点
简化接口:容器适配器通过隐藏底层容器的复杂接口,使用户能够更专注于特定的数据结构(如栈或队列)的特性。
灵活底层容器:容器适配器可以基于不同的底层容器构建,但需满足特定的要求。例如,栈可以用 deque 或 vector 作为底层容器。
与容器解耦:通过使用适配器,用户不需要关心底层容器的实现细节,只需专注于适配器提供的接口。
总体而言,容器适配器是一种设计模式,通过包装现有容器来提供定制化的数据结构接口,使程序设计更加简单和灵活。
栈和队列的模拟实现
我们通过适配器就能将栈和队列进行模拟实现了
stack.h
#pragma once#include<vector>#include<list>#include<deque>//template<class T>//class stack//{//private://T* a;//size_t _top;//size_t _capacity;//};// T(栈中存储的数据类型)和 Container(底层容器类型)/*当你在实例化这个模板类时,例如 stack<int, std::vector<int>> myStack;,编译器就会根据传入的模板参数 int 和 std::vector<int> 来推导出具体的 T 和 Container 类型。模板实例化:在编译阶段,编译器会用传递的模板参数类型 T 和 Container 来实例化这个模板类 stack,并生成相应的类定义。例如,如果你传入的是 stack<int, std::vector<int>>,编译器会生成一个 stack<int, std::vector<int>> 的具体实例,并将代码中所有的 T 替换为 int,Container 替换为 std::vector<int>。模板函数的调用:在使用这个栈的成员函数时,编译器也会根据实例化后的具体类型来判断类型。例如 _con.push_back(x); 调用时,编译器会检查 _con 是什么容器类型(在这种情况下是 std::vector<int>),从而验证 push_back 是否可以接受 int 类型的参数 x。*///T是元素的类型,这个Container是容器的类型,我们通过容器进行函数的调用操作namespace kai{//函数参数能加缺省值,那么我们的模版参数也是可以加缺省值的//如果我们没传的话就用的是缺省值,传了的话那么就用我们传的值//我们这里默认用的是一个deque的容器template<class T, class Container=deque<T>>//Container就是容器的意思,存的是底层的数据类型class stack{public:void push(const T& x){_con.push_back(x);}void pop()//不需要加参数 {_con.pop_back();//将尾部的数据pop掉}const T& top() const//返回栈顶位置数据{return _con.back();//直接返回尾部的数据,通用接口}size_t size() const{return _con.size();}bool empty() const{return _con.empty();}private:Container _con;};}queue.h
#pragma once#include<vector>#include<list>#include<deque>namespace kai{//deque既可以做栈也可以做队列的适配容器template<class T, class Container = deque<T>>//Container就是容器的意思,存的是底层的数据类型class queue//队尾入数据,队头出数据{//vector不能适配队列,这里不能头删public:void push(const T& x)//入队列--尾{_con.push_back(x);}void pop()// 出队列---头删{_con.pop_front();//将头部的数据pop掉}const T&front() const{return _con.front(); //直接返回头部的数据,通用接口}const T& back() const//返回栈顶位置数据{return _con.back();//直接返回尾部的数据,通用接口}size_t size() const{return _con.size();}bool empty() const{return _con.empty();}private:Container _con;};}test.h
#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>#include<stack>#include<queue>#include"stack.h"#include"Queue.h"using namespace std;int main(){kai::stack<int,list<int>>st;//前面是数据的类型。后面是容器的类型st.push(1);st.push(2);st.push(3);st.push(4);while (!st.empty())//不断取值直到栈为空{cout << st.top() << " ";st.pop();//头删替换下个数据}cout << endl;//这里的vector是会报错的,因为vector是不支持这里的pop的kai::queue<int, list<int>>q;//前面是数据的类型。后面是容器的类型q.push(1);q.push(2);q.push(3);q.push(4);while (!q.empty())//不断取值直到栈为空{cout << q.front() << " ";q.pop();//头删替换下个数据}cout << endl;return 0;}当你在实例化这个模板类时,例如 stack<int, std::vector> myStack;,编译器就会根据传入的模板参数 int 和 std::vector 来推导出具体的 T 和 Container 类型。
模板实例化:在编译阶段,编译器会用传递的模板参数类型 T 和 Container 来实例化这个模板类 stack,并生成相应的类定义。例如,如果你传入的是 stack<int, std::vector>,
编译器会生成一个 stack<int, std::vector> 的具体实例,并将代码中所有的 T 替换为 int,Container 替换为 std::vector。
模板函数的调用:在使用这个栈的成员函数时,编译器也会根据实例化后的具体类型来判断类型。例如 _con.push_back(x); 调用时,
编译器会检查 _con 是什么容器类型(在这种情况下是 std::vector),从而验证 push_back 是否可以接受 int 类型的参数 x。
deque的介绍
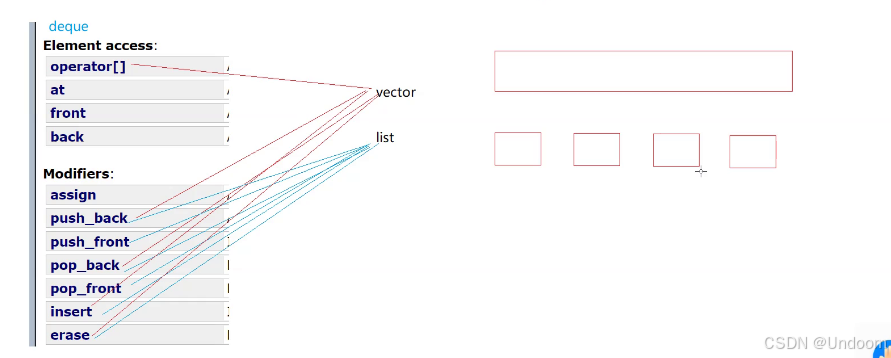
deque叫做双端队列,两端都可以进行插入删除的操作
头尾都可以支持插入删除数据的
deque的技能树点的比较满,啥都会
那么就说明deque就可以将list和vector的技能都带上
vector是一块连续的空间,list是一个个小块的空间通过指针进行连接起来的

deque的缺陷在哪里呢?
insert和erase
1.挪动后面所有数据,效率低
2.只挪动当前buffer的数据,每个buffer大小就不一样了,insert 、 erase的效率不错,但是[]的效率直线下降
deque的头尾插入删除的效率还是不错的
适当的下标访问可以使用deque
但是得大量的下标访问就不适合用deque了
所以栈和队列的适配容器是deque
deque的核心结构是迭代器进行支撑的
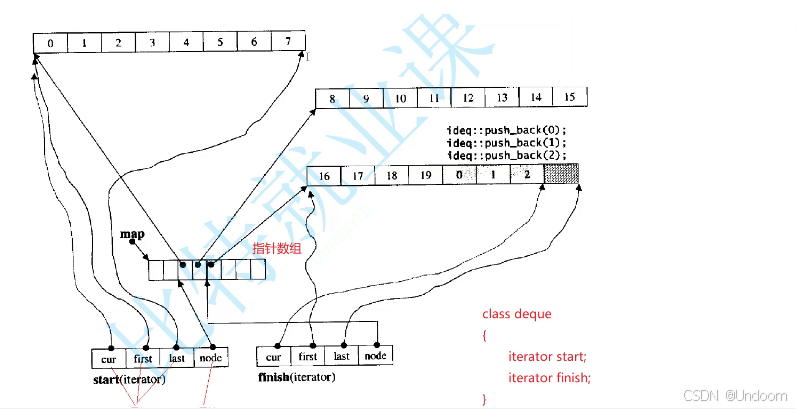
deque里面只有两个迭代器,start和finish
在 C++ 中,deque 是一种双端队列容器,允许在两端高效地插入和删除元素。尽管 deque 在某些方面具有优势,但在特定使用场景下仍然存在一些缺陷或限制:
1. 内存开销较高
deque 的内存布局并不像 vector 一样是连续的内存块,而是分段的。这使得 deque 会有额外的内存管理开销,因此其内存利用率通常比 vector 低。
对于需要大量小型数据结构的应用,deque 的内存分块可能带来一定的开销。
2.随机访问性能略低于 vector
虽然deque 支持随机访问(允许使用 operator[] 和 at),但由于 deque 是分块存储的,因此在访问元素时,尤其是访问中间位置的元素时,性能会略低于 vector,因为它需要定位具体的分块位置。 3. 与指针或迭代器的兼容性r
deque 的指针或迭代器在插入和删除操作后可能会失效,尤其是在中间插入或删除元素时。
虽然 deque 的头尾插入操作不会像 vector 一样导致整个容器重新分配,但在扩展容量时,它可能会重新配置分块,这会导致指针和迭代器失效。
4. 不适合用于需要频繁中间插入和删除的场景
deque 在头尾的插入和删除操作效率很高,但在中间位置插入或删除元素时会导致较多的数据移动,从而影响性能。因此,如果需要频繁在中间位置进行插入或删除操作,deque 不是最佳选择,list 或 std::vector(如果可以接受一定的重新分配开销)可能会更合适。 5. 在特定平台上的实现不一致
不同的编译器和标准库实现可能会对deque 采用不同的分块策略。这可能导致在不同平台上的性能和内存使用情况有所不同,从而带来一些不可预测的行为。 6. 缺乏shrink_to_fit支持
C++ 标准中没有要求deque 支持 shrink_to_fit,即使进行了删除操作,deque 可能不会自动释放不再使用的内存,导致可能的内存浪费。 总结
deque 在需要高效的双端插入和删除操作时非常有用,但在需要频繁的中间操作或更高的随机访问性能时,它的效率可能不如 vector。选择容器时应根据具体需求进行权衡,以最大限度地发挥各容器的优势。
题目
215. 数组中的第K个最大元素
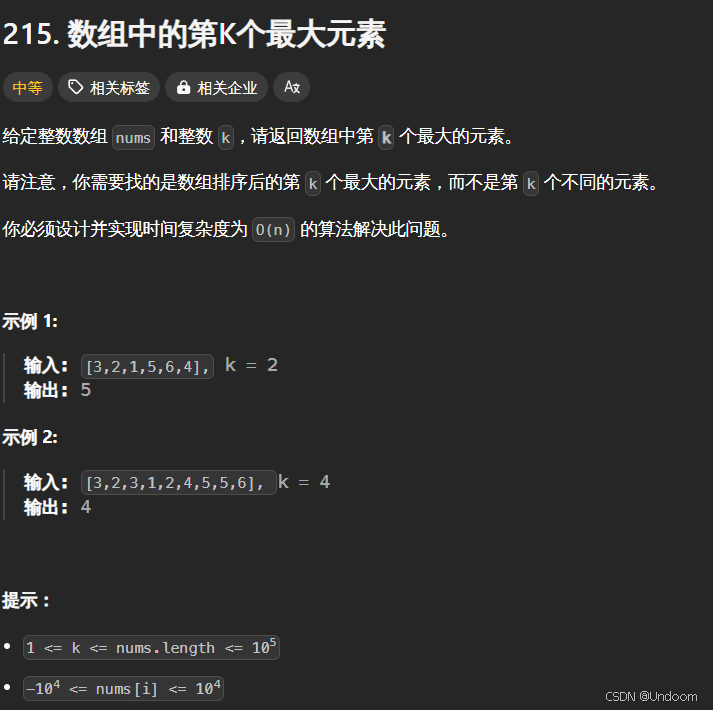
class Solution {public: int findKthLargest(vector<int>& nums, int k) { //将数组中的元素先放入到优先级队列中,默认是大堆 priority_queue<int> p(nums.begin(),nums.end()); //我们删除k-1次,那么循环结束的时候的堆顶的数据就是当前最大了的,我们直接返回堆顶数据就行了 while(--k)//--k是走k-1次,k--是走k次 { p.pop(); } return p.top(); }};priority_queue 优先级队列
默认是大的优先级最高
priority_queue 是一种基于优先级的队列数据结构,通常实现为一个堆(heap),可以支持快速插入和删除优先级最高的元素。在 priority_queue 中,元素的顺序不是按插入顺序排列的,而是根据优先级排序。通常有两种类型的优先队列:
最大优先队列:优先级最高的元素位于队列顶部(即最大值在最前面)。
最小优先队列:优先级最低的元素位于队列顶部(即最小值在最前面)。
以下是一些关于 priority_queue 的关键操作:
插入元素:将新元素插入到队列中,优先级队列会自动调整元素的位置。
访问队首元素:访问优先级最高的元素(在最大优先队列中为最大值,在最小优先队列中为最小值)。
删除队首元素:删除优先级最高的元素。
判断队列是否为空:检查队列中是否有元素。
在 C++ 标准模板库(STL)中,priority_queue 的使用非常常见,以下是一个简单的代码示例:
#include <iostream>#include <queue>int main() { std::priority_queue<int> maxQueue; // 默认是最大优先队列 // 插入元素 maxQueue.push(10); maxQueue.push(30); maxQueue.push(20); maxQueue.push(5); // 输出并删除最大元素 while (!maxQueue.empty()) { std::cout << maxQueue.top() << " "; maxQueue.pop(); } return 0;}使用最小优先队列
在 C++ 中,要创建最小优先队列,可以使用以下方式:
std::priority_queue<int, std::vector<int>, std::greater<int>> minQueue;使用场景
任务调度:例如操作系统中的任务调度器,根据任务的优先级调度执行任务。
路径查找:如 Dijkstra 算法使用优先队列来找到最短路径。
事件驱动模拟:在模拟系统中用来根据事件的优先级处理事件。
priority_queue 是一种非常高效的数据结构,适合需要频繁处理优先级数据的场景。
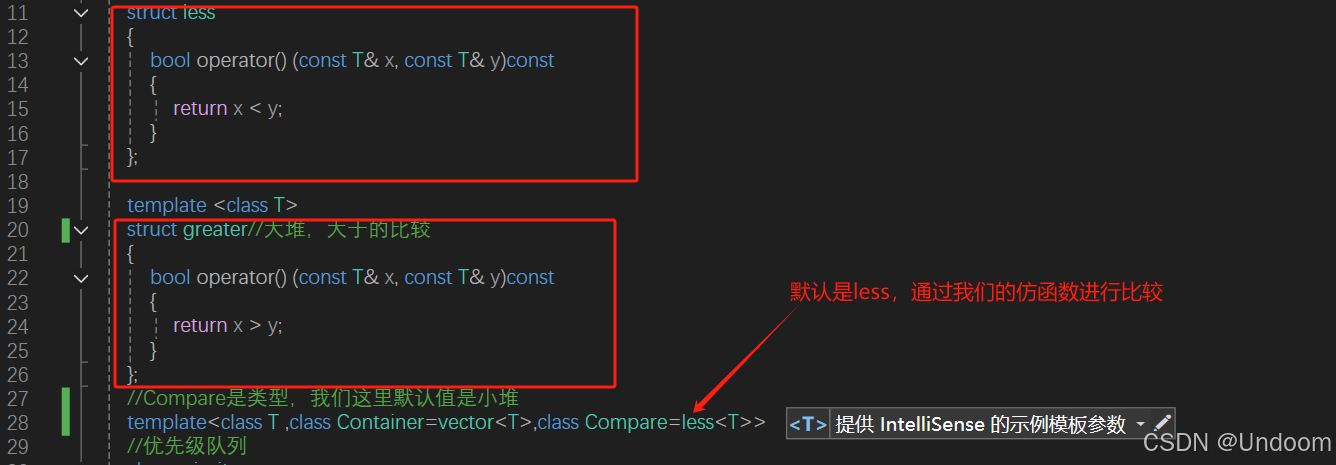
int main(){//优先级队列//优先级默认是大的优先级高//priority_queue<int> pq;//下面的就是小的优先级高了priority_queue<int,vector<int>,greater<int>> pq;//前面是数据的类型。后面是容器的类型pq.push(3);pq.push(2);pq.push(1);pq.push(4);while (!pq.empty())//不断取值直到栈为空{cout << pq.top() << " ";pq.pop();//头删替换下个数据}return 0;} priority_queue的模拟实现
#pragma once#include<vector>//默认是vector进行适配的//堆是将数组看成完全二叉树的//假设p是父亲,那么2*p+1是左孩子,2*p+2是右孩子//所以对于子节点的话,-1然后/2就能算到父亲节点的下标了namespace kai{//仿函数//对象可以像函数一样进行使用,因为他重载了operator()template <class T>struct less{bool operator() (const T& x, const T& y)const{return x < y;}};template <class T>struct greater//大堆,大于的比较{bool operator() (const T& x, const T& y)const{return x > y;}};//Compare是类型,我们这里默认值是小堆template<class T ,class Container=vector<T>,class Compare=less<T>>//优先级队列class priority_queue{public:priority_queue() = default;//default是强制生成//我们不写默认构造的话那么就会调用对应类型的默认构造函数了template<class InputIterator>//构造函数priority_queue(InputIterator first, InputIterator last)//这里传的是迭代区间:_con(first,last)//直接用这个迭代区间进行初始化的操作{//进行建堆的操作/*在构建堆(特别是最大堆或最小堆)的过程中,我们之所以从倒数第一个非叶子节点开始,是因为叶子节点本身已经是一个有效的堆。下面是具体原因和背后的逻辑:1. **叶子节点天然满足堆性质**:堆的性质要求每个节点的值满足特定条件,比如最大堆要求每个节点的值大于或等于其子节点的值,最小堆要求每个节点的值小于或等于其子节点的值。叶子节点没有子节点,自然满足堆的定义。所以我们无需对叶子节点进行任何调整。2. **从倒数第一个非叶子节点开始可以逐层调整堆**:如果我们从倒数第一个非叶子节点开始进行“下沉”操作(即调整该节点与其子节点的关系以满足堆的性质),则可以逐步调整每一层节点,从而最终得到一个完整的堆结构。这个过程叫做“自底向上”建堆,从倒数的非叶子节点开始,避免重复调整上层节点,提高了构建效率。3. **提高构建效率**:构建堆的时间复杂度是 \(O(n)\),而不是 \(O(n \log n)\),因为从倒数第一个非叶子节点开始向上调整,比从根节点开始构建效率高得多。倒数的非叶子节点数量较少,而且每个节点的调整次数随深度的增加而减少,这种方式在平均情况下只需执行有限的调整操作。4. **构建过程的稳定性**:自底向上从非叶子节点开始构建可以保证堆的结构稳定,不会因为上层节点的调整而打乱下层已经满足堆性质的节点。这保证了最终得到的是一个合法的堆。因此,从倒数第一个非叶子节点开始建堆是一种高效、合理的方式。*/for (int i = (_con.size()-1-1)/2; i >=0; i--){//这里的第一个-1是最后一个数的下标,第二个-1配合外面的/2可以找到我们的父亲节点,这个节点就是倒数第一个非叶子节点了,我们从这个开始进行建堆的操作//我们从这个位置开始进行调整,不断的调整到根节点//向下调整算法要求左右子树都是大堆的,不然是无效的AdjustDown(i);}//我们从倒数第一个非叶子节点进行建堆的操作可以保证堆的结构正确}//向上调整算法void AdjustUp(int child){Compare com;int parent = (child - 1) / 2;//算出父亲节点的下标位置while (child > 0){//if (_con[parent]<_con[child] )//父亲小于孩子,实现大堆if (com( _con[parent],_con[child]))//利用com对象进行比较大小,我们这里的默认传的是greater{//直接利用C++中的swap函数进行交换就行了swap(_con[child], _con[parent]);//将父亲节点和子节点的值进行交换的操作child = parent;//然后我们的孩子节点就跑到了父亲节点的位置了parent = (parent - 1) / 2;//然后父亲节点的位置就跑到了当前父亲节点的父亲节点那里了}else{//如果调整的过程中孩子节点的值比父亲节点的值大了,我们就直接跳出循环就行了,不进行操作了break;} }}void push(const T& x)//在堆中继续数据的插入的操作{//先插入x_con.push_back(x);//进行向上调整(小堆)AdjustUp(_con.size() - 1);//size-1就是最后一个数据的位置的下标,然后我们利用向上调整算法进行调整的操作}void AdjustDown(int parent){Compare com;size_t child = parent * 2 + 1;//通过给的父亲的位置算出左孩子的位置while (child<_con.size()){//我们这里是小堆//假设,选出左右孩子中小的那个孩子//if (child + 1 < _con.size() && _con[child]<_con[child + 1] )//如果右孩子存在的话,并且右孩子大于左孩子的话if (child + 1 < _con.size() && com(_con[child],_con[child + 1] ))//如果右孩子存在的话,并且右孩子大于左孩子的话{++child;//那么我们就将我们的孩子节点定位到右孩子的位置那里}if (com(_con[parent],_con[child] ))//如果当前孩子节点小于父亲节点的话{//我们就将小的节点往上面进行交换swap(_con[child], _con[parent]);parent = child;//然后我们父亲节点就定位到当前的孩子节点了child = parent * 2 + 1;//算出当前孩子节点的孩子节点}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);//交换堆顶数据和最后一个数据_con.pop_back();//然后将最后一个数据进行时删除的操作就行了//进行向下调整的操作,从根位置开始向下进行调整的操作AdjustDown(0);}bool empty()//判空函数{return _con.empty();}const T& top()//返回堆顶的数据{return _con[0];//就是返回根位置的数据就行了}size_t size(){return _con.size();}private:Container _con;//存放数据的容器};}仿函数的介绍
//仿函数//对象可以像函数一样进行使用,因为他重载了operator()template <class T>struct Less{bool operator() (const T& x, const T& y)const{return x < y;}};template <class T>struct Greater{bool operator() (const T& x, const T& y)const{return x > y;}};int main(){Less<int> lessFunc;cout << lessFunc(1, 2) << endl;cout << lessFunc.operator()(1, 2) << endl;return 0;}仿函数(Functor)是一种在C++和其他编程语言中使用的技术,它使得对象可以像函数一样被调用。仿函数通常通过重载 operator() 操作符来实现,使得一个对象可以像函数那样接受参数并返回结果。仿函数的主要优势在于它将函数的功能和状态封装到对象中,使得函数调用更加灵活、模块化和可扩展。
仿函数的基本概念
在C++中,可以通过重载 operator() 操作符来定义一个仿函数,使得一个对象可以像普通函数一样被调用。仿函数通常定义为一个类的成员函数,允许该类的对象具备类似函数的行为。
仿函数的基本用法
下面是一个简单的仿函数示例,通过重载 operator() 来实现一个加法仿函数:
#include <iostream>class Adder {public: int operator()(int a, int b) const { return a + b; }};int main() { Adder add; int result = add(3, 4); // 对象像函数一样被调用 std::cout << "Result: " << result << std::endl; // 输出 Result: 7 return 0;}在这个例子中,Adder 类重载了 operator() 操作符,使得其对象 add 可以像一个函数一样通过 add(3, 4) 的形式来调用,返回结果 7。
仿函数的优点
灵活性:仿函数可以携带状态,可以存储数据和维护状态,适合需要保存计算状态的场景。
性能优化:由于仿函数是类的一部分,它们可以通过内联函数进行优化,从而获得比普通函数指针更好的性能。
可定制性:可以根据需求重载多个 operator(),使得对象可以接收不同类型和数量的参数。
更符合面向对象设计:仿函数可以使用类的其他成员和方法,因此可以实现更复杂的操作和逻辑。
常见的仿函数应用
STL 算法配合使用:标准库中的许多算法,如 std::sort、std::for_each 等都可以接受仿函数作为参数。
Lambda表达式的替代:在没有Lambda表达式的C++版本中,仿函数被广泛用于类似的场景。
策略模式:在设计模式中,仿函数常用于实现策略模式,用于传递可定制的算法。
示例:在STL中使用仿函数
#include <iostream>#include <vector>#include <algorithm>class MultiplyBy { int factor;public: MultiplyBy(int f) : factor(f) {} int operator()(int value) const { return value * factor; }};int main() { std::vector<int> values = {1, 2, 3, 4, 5}; std::transform(values.begin(), values.end(), values.begin(), MultiplyBy(3)); for (int value : values) { std::cout << value << " "; // 输出 3 6 9 12 15 } return 0;}在这个例子中,我们定义了一个 MultiplyBy 仿函数类,用于将每个元素乘以一个特定因子。然后使用 std::transform 将 MultiplyBy(3) 仿函数应用于容器中的每个元素。
总结
仿函数通过重载 operator() 来赋予对象函数的能力,使得它们能够和函数指针、Lambda表达式等互相替代并发挥作用。在C++编程中,仿函数广泛应用于STL算法和其他需要灵活函数调用的场景。

class Date{public:Date(int year = 1900, int month = 1, int day = 1) : _year(year) , _month(month) , _day(day) {} bool operator<(const Date& d)const { return (_year < d._year) || (_year == d._year && _month < d._month) || (_year == d._year && _month == d._month && _day < d._day); } bool operator>(const Date& d)const { return (_year > d._year) || (_year == d._year && _month > d._month) || (_year == d._year && _month == d._month && _day > d._day); } friend ostream& operator<<(ostream& _cout, const Date& d);private: int _year; int _month; int _day;};//声明和定义分离ostream& operator<<(ostream& _cout, const Date& d){ _cout << d._year << "-" << d._month << "-" << d._day; return _cout;}struct DateLess{ bool operator() (const Date* d1, const Date* d2)//传过来的是两个指针,我们希望的是两个指针指向的值进行比较 { //我们直接进行解引用进行比较的操作 return *d1 < *d2; }};int main(){ // 大堆,需要用户在自定义类型中提供<的重载 kai::priority_queue<Date*,vector<Date*>,DateLess> q1;//优先级队列 q1.push(new Date{2024,10,23}); q1.push(new Date{2024,5,27}); q1.push(new Date{2024,11,7}); while (!q1.empty())//不断取值直到栈为空{cout << *q1.top() << " ";q1.pop();//头删替换下个数据}cout << endl;return 0; return 0;}题目
155.最小栈
题目
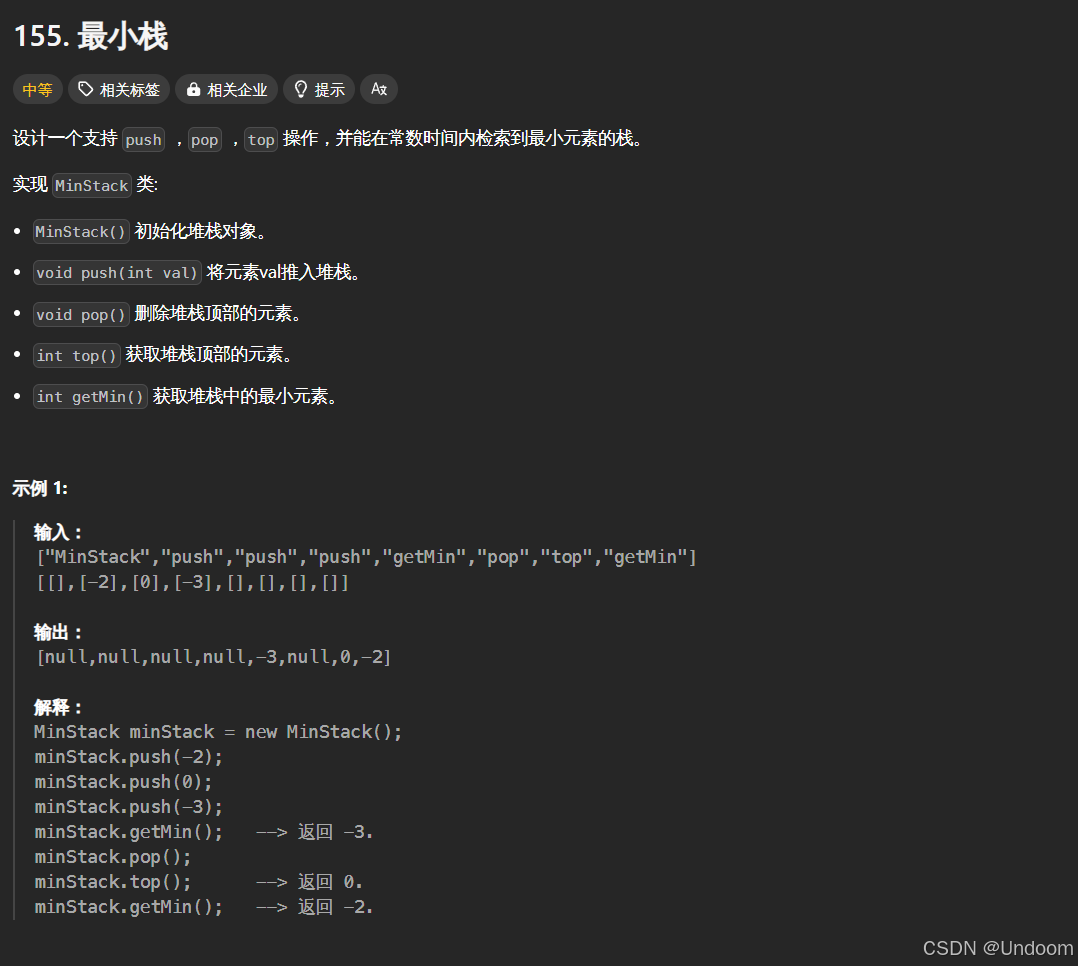
class MinStack{public: MinStack() { } void push(int val) { _st.push(val);//我们的st这个栈正常插入数据 if(_minst.empty()||val<=_minst.top())//如果_minst这个栈为空的话或者传过来的val小于等于_minst栈顶的元素的话,我们就将数据插入到minst中 { //如果这个minst这个栈是空的话,我们就进行数据的同步插入,如果这个插入数据小于我们的minst栈顶的数据的话我们就进行最小元素的更新操作,如果我们插入的元素等于我们的minst栈顶的元素的话,就是等于我们当前minst这个栈栈顶的最小元素的话,我们也是需要进行插入, _minst.push(val); } } void pop() { if(_st.top()==_minst.top()) { //如果st这个栈和minst这个栈的栈顶元素都相等的话,那么我们都需要进行删除操作的 _minst.pop(); } _st.pop();//st这个栈正常进行删除操作,我们需要对minst这个栈进行一个判断操作,如果当前两个栈的栈顶元素相同的话,那么我们就进行minst这个栈的栈顶元素的删除操作 } int top() { return _st.top();//返回我们的st这个栈的栈顶元素就行了 } int getMin() { //获取最小值的话我们就将minst这个栈的栈顶元素进行返回就行了,因为这个栈是进行插入元素中最小的元素的更新的 return _minst.top(); }private://通过两个栈我们实现了找到最小元素的功能了/*如果我们的st存入5的话,然后我们的minst记录当前的最小值存放栈中,就是存放5然后存入4,那么st存入4,minst也存入4,更新最小值然后我们st存放6,那么我们的minst更新最小值还是4然后我们放入1的话,minst更新最小值,那么就存入1了如果我们要pop我们的st栈顶元素的话,那么我们的minst同样更新最小值,那么最小值就变成上一个最小值4了这个MinStack这个类我们是不需要写默认构造的,编译器默认生成一个无参的构造这里我们的自定义类型st和minst会自动调用自己的构造函数的,我们是不需要显示写的*/ stack<int> _st; stack<int> _minst;};/** * Your MinStack object will be instantiated and called as such: * MinStack* obj = new MinStack(); * obj->push(val); * obj->pop(); * int param_3 = obj->top(); * int param_4 = obj->getMin(); */通过两个栈我们实现了找到最小元素的功能了
如果我们的st存入5的话,然后我们的minst记录当前的最小值存放栈中,就是存放5
然后存入4,那么st存入4,minst也存入4,更新最小值
然后我们st存放6,那么我们的minst更新最小值还是4
然后我们放入1的话,minst更新最小值,那么就存入1了
如果我们要pop我们的st栈顶元素的话,那么我们的minst同样更新最小值,那么最小值就变成上一个最小值4了
在我们的st这个栈在插入的时候我们的minst不断进行最小元素的更新操作
但是如果我们想:如果在st中插入的好几个数据都是重复的话那么我们的minst这个栈就显得很麻烦了
那么我们就可以将我们的minst这个栈改造下
我们可以在minst中对存入的数据进行最小值更新的同时并且进行计数的操作
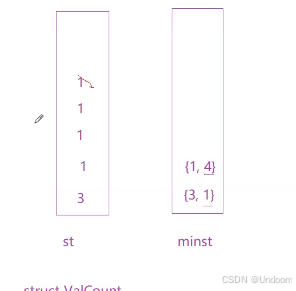
JZ31 栈的压入、弹出序列
题目
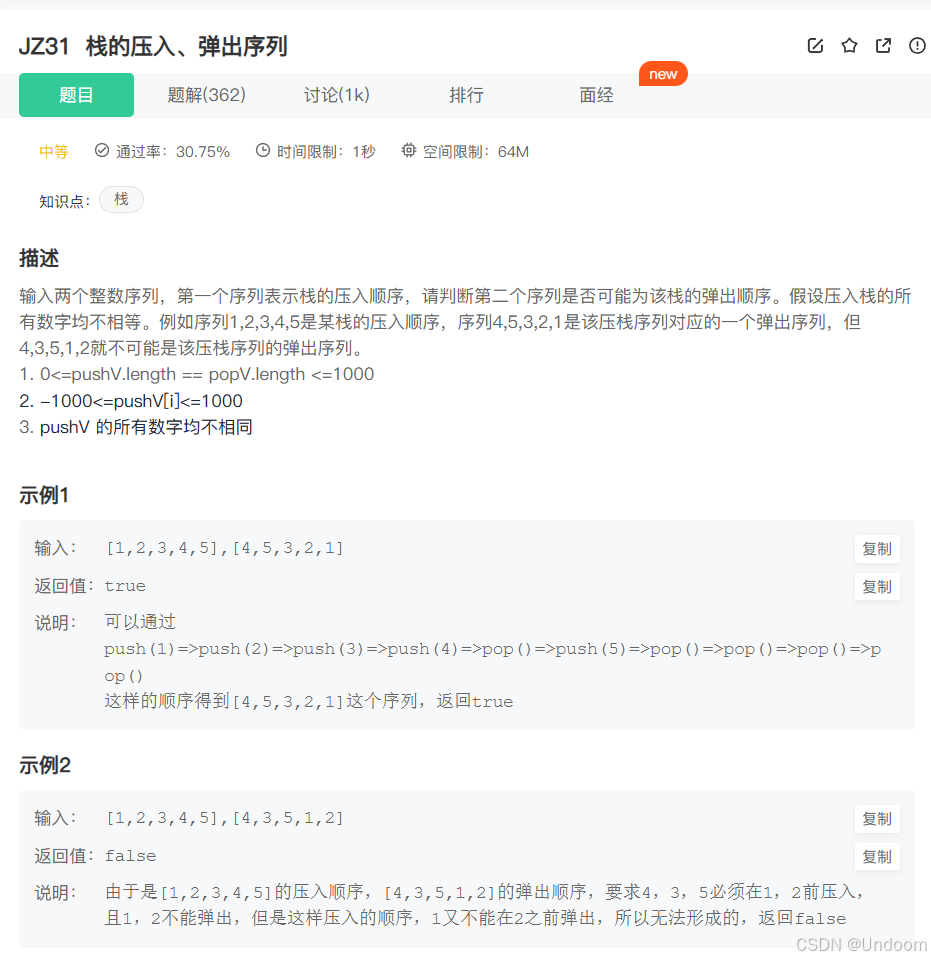

1.先入栈pushi位置的数据
2.栈顶数据跟出栈popi序列位置数据比较,如果匹配则出栈,那么popi++,如果不匹配的话,那么我们继续重复第一个操作
结束条件就是直到我们的栈是空的,匹配完了
class Solution {public: /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * * * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型 */ bool IsPopOrder(vector<int>& pushV, vector<int>& popV) { size_t pushi=0,popi=0; stack<int>st; while(pushi<pushV.size()) { //我们先往st这个栈中插入pushv中pushi指向的元素,然后pushi进行加加操作 st.push(pushV[pushi++]);//这个是我们入的数据 //入完数据之后我们进行一个比较的操作 while(!st.empty()&&popV[popi]==st.top()) { //如果这个st这个栈不是空的并且我们的popv这个数组中i指向的元素和st中的元素是相等的话,那么我们就进行出栈操作,进了st之后又出就是这个意思 popi++;//换下一个数据进行比较 st.pop();//删除当前栈的栈顶数据 } } return st.empty(); }};/*两个数组1 2 3 4 5 pushi4 3 5 1 2 popi我们先将1进行入栈,然后与popi指向的元素进行比较,不匹配,我们继续进行入栈入栈了2 3 4到了4这里,我们的pushi和篇popi指向的数据进行了匹配了然后我们删除了当前的这个4这个元素,我们将popi++,那么就指向了3然后我们还是处于循环中,我们判断的pushi和popi指向的数据是否匹配,然后此时的栈顶元素是3,匹配上了,到了然后将3删除了然后我们此时的栈顶元素是2,但是我们的popi指向了5,那么我们就出了循环,继续进行入栈的操作了,将最后的5入栈了。然后我们匹配上了,将5进行删除了然后我们在循环之中继续进行判断是否匹配,我们的此时栈顶元素是2,但是我们的popi指向的元素是1,然后我们又出循环了,然后我们进行入栈操作,但是我们的pushi已经越界了,那么就出了外循环了,然后我们的循环就终止了,然后我们判断我们的栈是不是空的,如果是空的话那么我们就返回了true,如果不是空的话那么就返回false*/如果是匹配的话,那么最后栈的空间里面肯定是空的,如果不匹配的话那么肯定是不匹配的
150. 逆波兰表达式求值
题目

class Solution {public: int evalRPN(vector<string>& tokens) { stack <int>s; for(auto &str:tokens) { //如果是操作符的话 if("+"==str||"-"==str||"*"==str||"/"==str) { //如果遇到操作符的话我们就从栈里面拿出两个数字进行操作符的运算操作 //我们先拿出来的是右操作符,然后是左操作符 int right=s.top();//拿完一个元素之后我们删除这个栈顶元素换新的元素当栈顶元素 s.pop(); int left=s.top(); s.pop(); switch(str[0]) { case '+': s.push(left+right); break; case '-': s.push(left-right); break; case '*': s.push(left*right); break; case '/': s.push(left/right); break; } } else//如果是操作数的话 { s.push(stoi(str));//stoi的作用是将字符串转换为整型,然后放到栈里面去 } } return s.top();//最后保存的就是我们的结果 }};232. 用栈实现队列
题目
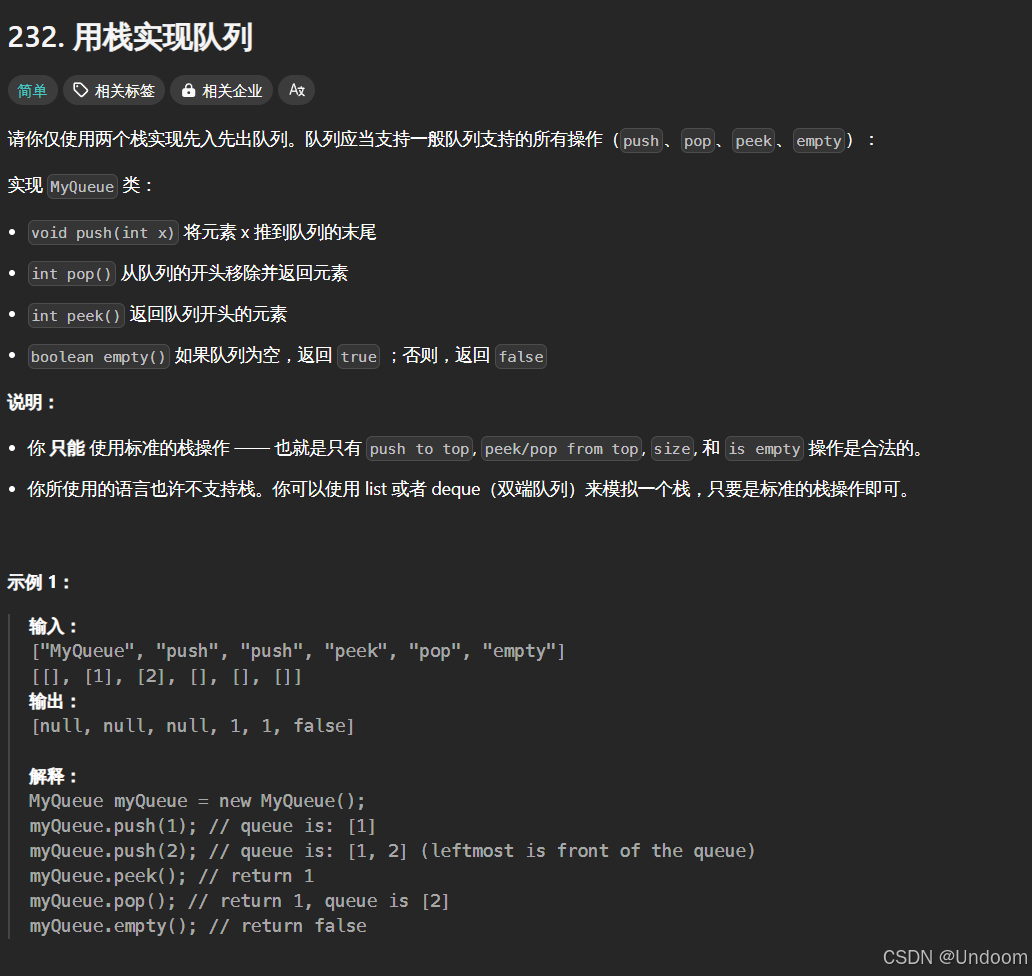
class MyQueue{private: stack<int> stackIn; stack<int> stackOut; //辅助函数,将所有元素从stackIn移动到stackOut void move() { while(!stackIn.empty())//In这个栈不是空的那么就进行循环操作 { stackOut.push(stackIn.top()); stackIn.pop(); } }public: MyQueue()//构造函数不写 {} //将元素x推入队列的末尾 ,这里我们的新元素入栈到in栈里面 void push(int x) { stackIn.push(x); } //移除队列的开头元素并返回队列开头元素 int pop() { if(stackOut.empty())//如果out这个栈为看空的话,那么我们就将in栈的元素全部移动到out的栈里面 { move();//直接利用我们上面写的辅助函数进行操作就行了 } int result=stackOut.top(); stackOut.pop(); return result;//返回out栈的栈顶元素 } //返回队列开头的元素 int peek() { if(stackOut.empty())//如果out栈是空的话,那么我们将in的元素全部移动到out的栈 { move(); } return stackOut.top(); } //如果队列是空的,返回true;否则返回false bool empty()//两个栈都是空的话那么这个队列就是空的 { return stackIn.empty()&&stackOut.empty(); }};/** * Your MyQueue object will be instantiated and called as such: * MyQueue* obj = new MyQueue(); * obj->push(x); * int param_2 = obj->pop(); * int param_3 = obj->peek(); * bool param_4 = obj->empty(); */225. 用队列实现栈
题目
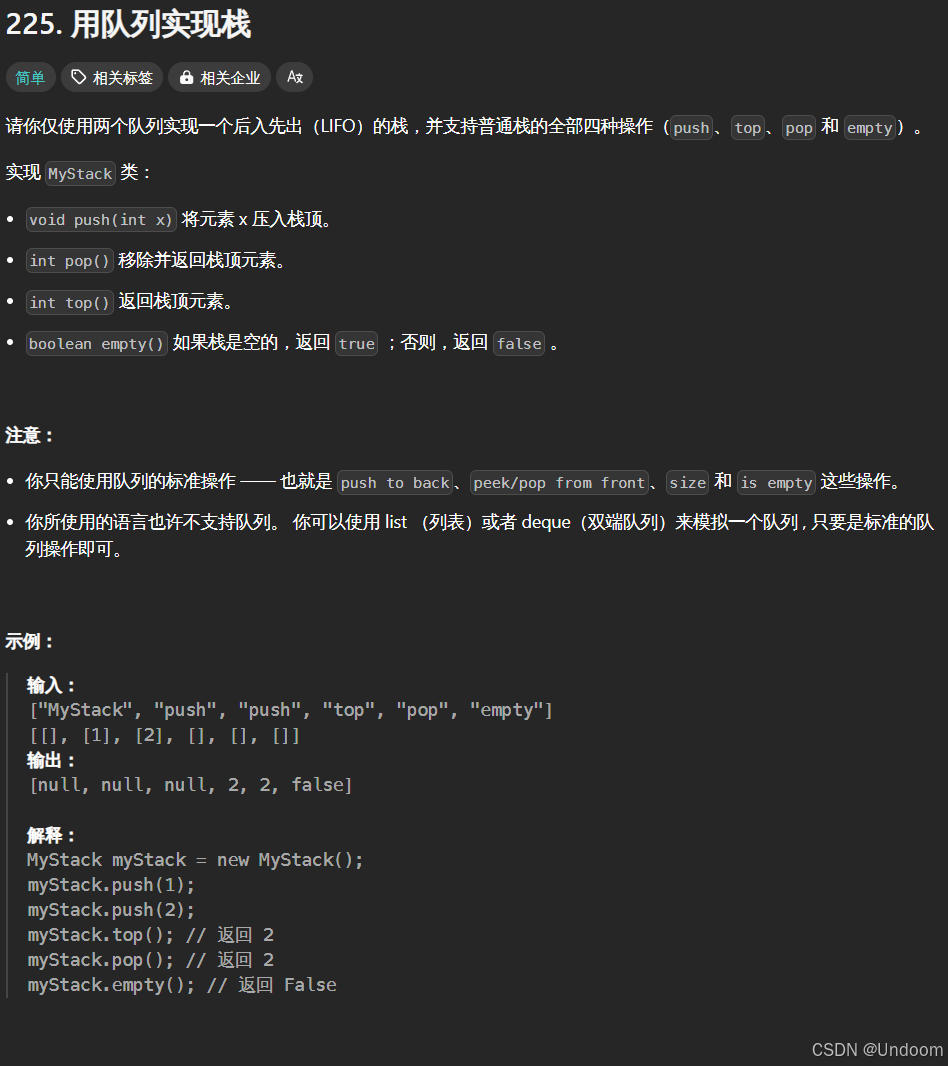
class MyStack{private: queue<int> queue1; queue<int> queue2;public: MyStack() {} //压入元素到栈顶,后入先出 void push(int x) { queue2.push(x);//先将元素插入到队列2中 while(!queue1.empty())//只要队列1中有数据就进行循环操作 { queue2.push(queue1.front()); queue1.pop(); } //将两个队列进行交换的操作 swap(queue1,queue2); } // 移除栈顶元素,栈顶元素在 queue1 的队首,因此直接 pop 并返回该元素。 int pop() { int topment=queue1.front(); queue1.pop(); return topment; } int top() { return queue1.front(); } bool empty() { return queue1.empty(); }};/** * Your MyStack object will be instantiated and called as such: * MyStack* obj = new MyStack(); * obj->push(x); * int param_2 = obj->pop(); * int param_3 = obj->top(); * bool param_4 = obj->empty(); */