前言
一、搜索二叉树
1.什么是搜索二叉树
搜索二叉树又叫做二叉排序树,它可以是一颗空树,或者是具有以下性质的树
如果它左子树不为空,左子树上所有节点的值都小于等于根节点的值如果它右子树不为空,右子树上所有节点的值都大于等于根节点的值它的左右子树也都是搜索二叉树。在搜索二叉树中,可以支持插入相同的值,也可以不支持插入相同的值;
在map/set/multimap/multidset等系列式容器底层就是搜索二叉树,其他map/set不支持数据冗余(不支持插入相同的值);multimap/multiset支持数据冗余。
这里看一下不支持数据冗余的搜索二叉树:
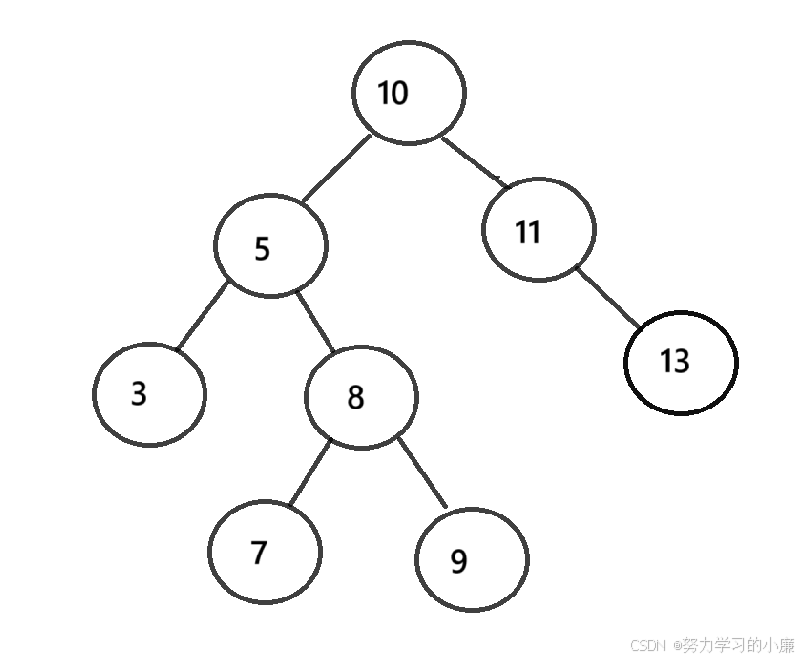
2. 搜索二叉树分析
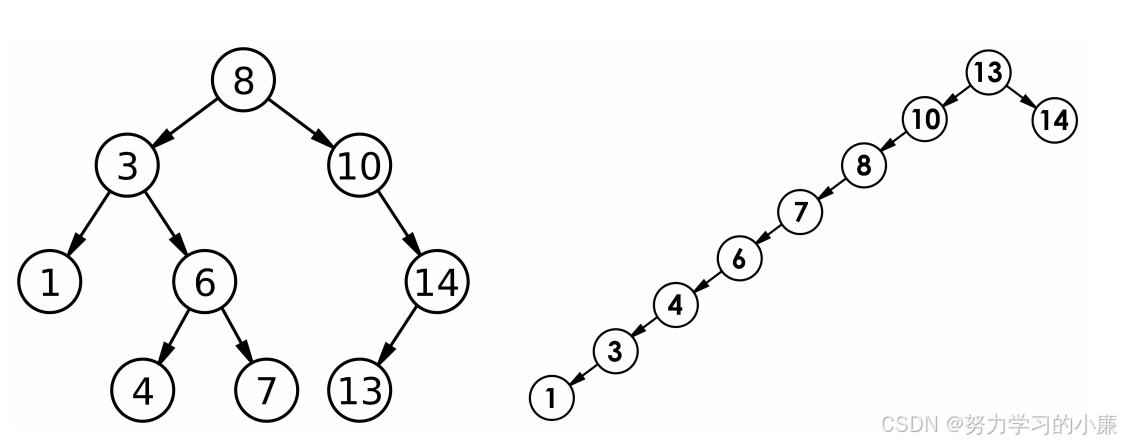
在最优情况下:搜索二叉树为完全二叉树,其高度是:log2 N
在最差情况下:搜索二叉树为单支树,其高度为N
综合而言,其时间复杂度为O(N)
而map和set底层为AVL树和红黑树,并不是简单的搜索二叉树,那样才适用于我们在内存中存储和搜索数据。
补充:
根据搜索二叉树的原理,当我们中序遍历这个二叉树时,这个数据是有序的。
左子树、根节点、右子树(左子树 < 根节点 < 右子树)。
3. 搜索二叉树的插入
根据搜索二叉树的特点,那在插入的过程中,就要根据插入的值来判断其应该插入到哪里。
如果树为空,就新创建节点,该节点节为树的根节点。如果树不为空,则根据搜索二叉树特点,从根节点遍历二叉树,比节点值大则遍历其右子树;比节点值小则遍历其左子树。如果插入相等的值,可以支持插入,也可以不支持;支持的话可以插入其左子树也可以插入其右子树。代码实现
//二叉搜索树//节点template<class T>struct BSTreeNode{T _val;BSTreeNode* _left;BSTreeNode* _right;BSTreeNode(const T& x):_key(x), _left(nullptr), _right(nullptr){}};//BSTreetemplate<class T>class BSTree{typedef BSTreeNode<T> Node;public://默认构造BSTree():_root(nullptr){}//插入bool insert(const T& x){if (_root == nullptr){_root = new Node(x);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (x > cur->_key){parent = cur;cur = cur->_right;}else if (x < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}Node* newnode = new Node(x);if (x < parent->_key){parent->_left = newnode;}else if (x > parent->_key){parent->_right = newnode;}return true;}private:Node* _root;};4. 搜索二叉树的查找
查找根插入有些相似,也是从根节点开始遍历,比节点值大就遍历其右子树;否则遍历其左子树。
从根节点开始遍历比节点值大,则遍历其右子树,比节点值下就遍历其左子树,相等则找到,返回true。遍历结束还没找到,则返回false,表示查找的值不存在。 代码实现
//查找bool find(const T& x){Node* cur = _root;while (cur){if (x > cur->_key){cur = cur->_right;}else if (x < cur->_key){cur = cur->_left;}else{return true;}}return false;}5. 搜索二叉树的删除
搜索二叉树的删除就有些复杂了,因为我们删除之后还要保持搜索二叉树的结构。
查找元素是否存在,存在就进行删除,否则返回false。
删除元素,根据删除元素所在节点的位置可以分为一下四种情况
该节点是叶子结点:其左右孩子节点都为空该节点左孩子节点为空,右孩子节点不为空该节点右孩子节点为空,左孩子节点不为空该节点左右孩子节点都不为空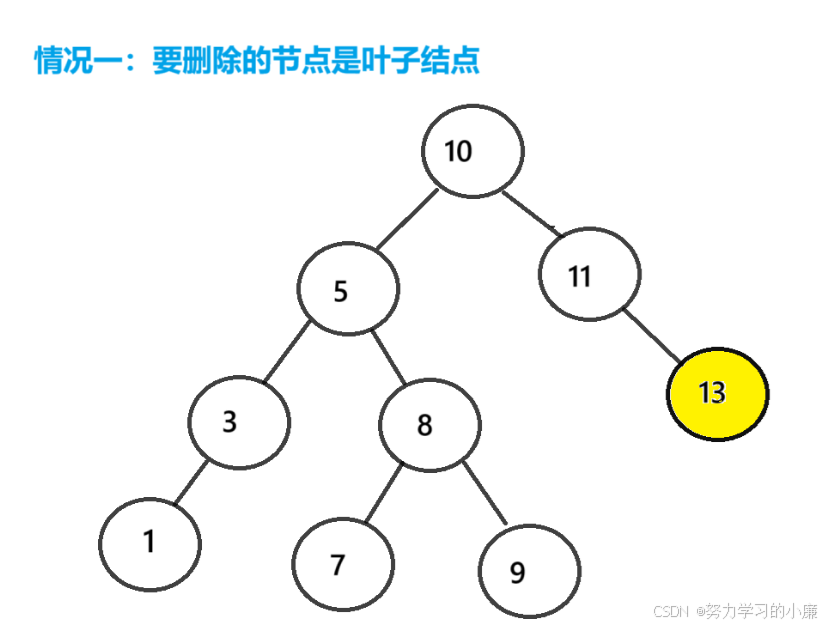
把删除节点的父节点对于的指针指向nullptr,然后删除该节点即可
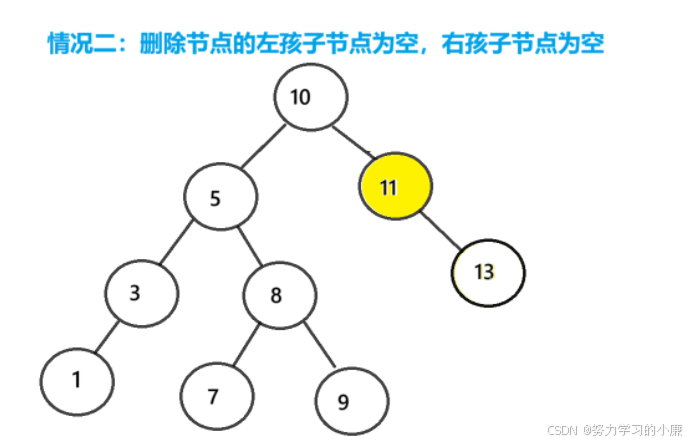
把删除节点的父节点的对应指针指向删除节点的右孩子节点,然后删除该节点即可。
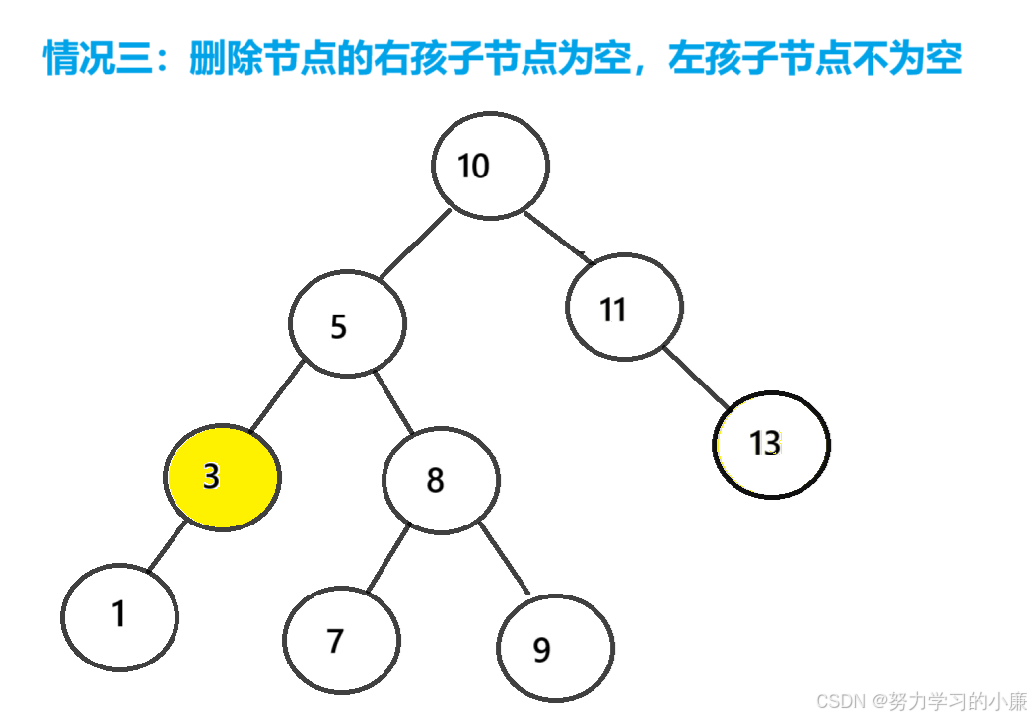
把删除节点的父节点的对应指针指向删除节点的左孩子节点,然后删除该节点即可。
我们观察这三种情况,处理的方式都有些相似,(像情况一,删除节点的左右孩子都为空,那我们也可以将它归于情况二或者情况三)
现在来看情况四:
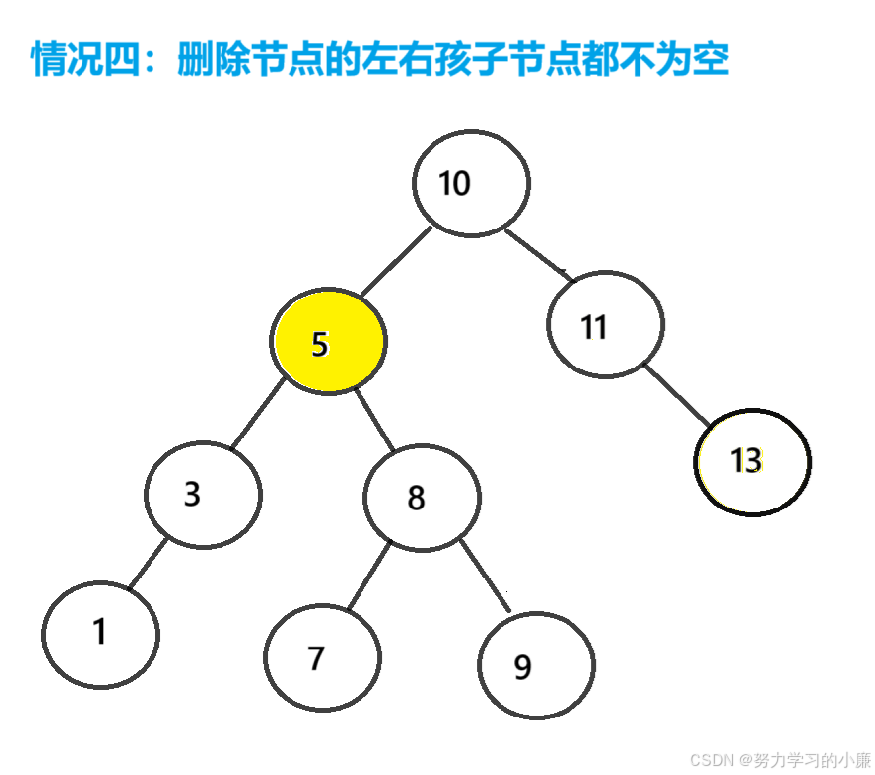
现在这种情况,我们就不能单纯的修改指针指向,然后删除了,(如果直接删除,那左右孩子节点就无处可去了);
要删除节点左右孩子节点都不为空
找到一个可以代替它的数,(可以寻找其右子树中最小的,也可以寻找其左子树中最大的)这个数的所在节点一定是以上三种情况的一种。然后将找到代替的值赋值到要删除的节点上(赋值以后要删除的节点就不用删除的,而是删除掉代替值所在的节点)这样可以说是偷梁换柱,将值给删掉了,节点的值修改成其他的了。代码实现
//删除bool erase(const T& x){Node* parent = _root;Node* cur = _root;while (cur){if (x > cur->_key){parent = cur;cur = cur->_right;}else if (x < cur->_key){parent = cur;cur = cur->_left;}else{if (cur->_left == nullptr)//左孩子为空或者左右孩子都为空{Node* del = cur;if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete del;}else if (cur->_right == nullptr) //右孩子为空{Node* del = cur;if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete del;}else //左右孩子都不为空{//在左子树中找最大的Node* left_max = cur->_left;Node* left_max_p = cur;while (left_max->_right){left_max_p = left_max;left_max = left_max->_right;}//赋值cur->_key = left_max->_key;//然后删除left_maxif (left_max_p->_left == left_max){left_max_p->_left = left_max->_left;}else{left_max_p->_right = left_max->_left;}delete left_max;}return true;}}return false;}二、搜索二叉树的key与key/value 使用
上述内容,实现的是key结构是搜索二叉树,还用key/value结构;
什么意思呢,就是key/value结构,存储的不单单是key这一个关键码,还存在一个与关键码有对于关系的元素value。
1. key结构
只有key作为关键码,只需存在key即可,key就是需要搜索到的值,在搜索时只需要判断key在不在就行了;
在key场景中不能进行修改,如果修改了就有可能破坏搜索二叉树的结构。
2. key/value结构
每一个关键码key都有与之对应的value,value可以是任何类型的对象;不仅需要存储关键码key,还需存储value,增删查改还是以key为关键字进行;key/value的搜索二叉树,支持修改value但是不支持修改key。 key/value结构这里就不实现了,实现起来与key结构十分相似;
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws