目录
一、数组基础二、数组基本操作的具体实现 2.1 向数组中添加元素(增)2.2 根据索引获取元素值(查)2.3 根据元素值去查数组(查) 2.3.1 根据值查看数组中是否存在该元素2.3.2 根据值返回元素的索引 2.4 获取数组中最大值(最小值)的索引(查)2.5 根据索引修改元素值(改)2.6 交换两个元素(改)2.7 从数组中删除元素 (删)2.8 根据元素值删除该元素(查+删)2.9 删除数组中值最大(最小)的元素(查+删) 三、动态数组 3.1 基本概念3.2 动态数组时间复杂度分析 3.2.1 添加操作O(n)3.2.2 删除操作O(n)3.2.3 修改操作O(1)3.2.4 查询操作3.2.5 总结 3.3 动态数组均摊复杂度3.4 Python列表与字典操作时间复杂度 3.4.1 列表操作时间复杂度3.4.2 字典操作时间复杂度
一、数组基础
官方定义:
将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示。
翻译:
将数据码成一排进行存放

索引可以有语义,索引也可以没有语义
数组最大的优点:快速查询,时间复杂度O(1)
数组最好应用于“索引有语义”的情况
但是并不是所有有语义的索引都适用
比如身份证号: 13131413415153
数组也可以处理没有语义的情况
我们在这一章,主要处理索引没有语义的情况数组的使用
索引没有语义,如何表示没有元素?
如何添加元素?如何删除元素?
我们可以自己定义一个Array类,来实现一些简单的功能
定义自己的数组类 :

"""数组特点: 占用一段连续的内存空间,支持随机(索引)访问,且时间复杂度为O(1) 添加元素时间复杂度:O(n) 删除元素时间复杂度:O(n)"""class Arr: def __init__(self, capacity=10): """ 构造函数 :param capacity:数组最大容量,不指定的话默认为10 """ self._capacity = capacity # 数组的有效元素数目,初始化为0 self._size = 0 # 由于python的list是动态扩展的,而我们要实现底层具有固定容量, # 占用一段连续内存空间的数组,所以用None来作为无效元素的标识 self._data = [None] * self._capacity def __getitem__(self, item): """ 让Arr类支持索引操作 :param item: 索引 :return: 该索引对应位置上的元素值 """ return self._data[item] def getSize(self): """ 返回数组有效元素的个数 :return: 数组有效元素的个数 """ return self._size def getCapacity(self): """ 返回数组的容量 :return: 数组的容量 """ return self._capacity def isEmpty(self): """ 判断数组是否为空 :return: True为空,False为非空 """ return self._size == 0 def printArr(self): """ 对数组元素进行打印 """ for i in range(self._size): print(self._data[i], end=' ') print('\nSize: %d------Capacity: %d' % (self.getSize(), self.getCapacity()))二、数组基本操作的具体实现
2.1 向数组中添加元素(增)



def add(self, index, elem): """ 向数组中添加一个元素,注意数组占用的是一段连续的内存空间, 所以在添加元素后,数组还是要保证这个特点,因此需要将后面的元素都向后挪一个位置 而且注意需要从尾部开始挪,防止元素之间的覆盖 时间复杂度:O(n) :param index:添加元素所在的索引位置 :param elem:所要添加的元素值 """ # 判断插入的位置是否无效 if index < 0 or index > self._size: raise Exception('Add Failed. Require 0 <= index <= self._size.') # 判断数组是否已经满了 if self._size == self._capacity: # 默认扩容当前容量的二倍。容量翻倍要比容量加上一个固定值要好 # 这样做均摊复杂度为O(1),具体百度。 self._resize(self._capacity * 2) # 从尾部开始挪动元素,在index处腾出一个空间 # 一定要注意,在步长为负数的情况下,区间是左开右闭的,即(index-1, self._size-1], # 所以是index-1,与正常的左闭右开区间是相反的 for i in range(self._size - 1, index - 1, -1): self._data[i + 1] = self._data[i] # 将index处赋值为elem self._data[index] = elem # 数组有效元素值加1 self._size += 1有了上面这个插入数据的一般函数,还可以写两个比较特殊的函数,在数组的头部和尾部插入元素,只要直接调用add函数就行:
def addLast(self, elem): """ 向数组尾部添加元素 时间复杂度:O(1) :param elem: 所要添加的元素 """ # 直接调用add方法,注意不用再判断合法性了 self.add(self._size, elem) def addFirst(self, elem): """ 向数组头部添加元素 时间复杂度:O(n) :param elem: 所要添加的元素 """ # 直接调用add方法 self.add(0, elem)2.2 根据索引获取元素值(查)
def get(self, index): """ 获得索引index处的元素 时间复杂度:O(1) :param index: 数组索引 :return: 数组索引处的值 """ # 判断index的合法性,注意获取值的时候索引不能等于self._size if index < 0 or index >= self._size: raise Exception('Get Failed. Index is illegal.') return self._data[index]由此可写出两个特殊函数,为获取头部和尾部元素的函数,直接调用get函数即可:
def getFirst(self): """ 获得数组首位元素的值 :return: 首位元素的值 """ # 直接调用get函数,安全可靠 return self.get(0) def getLast(self): """ 获得数组末尾元素的值 :return: 末尾元素的值 """ # 直接调用get函数,安全可靠 return self.get(self._size - 1)2.3 根据元素值去查数组(查)
2.3.1 根据值查看数组中是否存在该元素
def contains(self, elem): """ 查看数组中是否存在元素elem,最好不要传入一个浮点数 时间复杂度:O(n) :param elem: 目标元素 :return: bool值,存在为真 """ # 遍历数组 for i in range(self._size): if self._data[i] == elem: # 找到了就返回True return True # 遍历完了还没找到,返回False return False2.3.2 根据值返回元素的索引
def find(self, elem): """ 在数组中查找元素,并返回元素所在的索引。 如果数组中存在多个elem,只返回最左边elem的索引 时间复杂度:O(n) :param elem: 目标元素 :return: 元素所在的索引,没找到则返回-1(无效值) """ # 遍历数组 for i in range(self._size): if self._data[i] == elem: # 找到就返回索引 return i # 没找到就返回-1 return -1 def findAll(self, elem): """ 找到值为elem全部元素的索引 时间复杂度:O(n) :param elem: 目标元素 :return: 一个列表,值为全部elem的索引 """ # 建立一个新的数组用于存储索引值 ret_list = Arr() # 遍历数组 for i in range(self._size): if self._data[i] == elem: # 找到就将索引添加进ret_list ret_list.addLast(i) return ret_list2.4 获取数组中最大值(最小值)的索引(查)
def get_Max_index(self): """ 获取数组中的最大元素的索引,返回最大元素的索引值 如果有多个最大值,默认返回最左边的那个索引 时间复杂度:O(n) :return: 最大元素的索引 """ if self.isEmpty(): raise Exception('Error, array is Empty!') # 记录最大值的索引,初始化为0 max_elem_index = 0 # 从索引1开始遍历,一直到数组尾部 for i in range(1, self._size): # 如果当前索引的值大于最大值索引处元素的值 if self._data[i] > self._data[max_elem_index]: # 更新max_elem_index,这样它还是当前最大值的索引 max_elem_index = i # 遍历完后,将数组的最大值索引返回 return max_elem_index def get_Min_index(self): """ 获取数组中的最小元素的索引,返回最小元素的索引值 如果有多个最小值,默认返回最左边的那个索引 时间复杂度:O(n) :return: 最小元素的索引 """ if self.isEmpty(): raise Exception('Error, array is Empty!') # 记录最小值的索引,初始化为0 min_elem_index = 0 # 从索引1开始遍历,一直到数组尾部 for i in range(1, self._size): # 如果当前索引的值小于最小值索引处元素的值 if self._data[i] < self._data[min_elem_index]: # 更新min_elem_index,这样它还是当前最小值的索引 min_elem_index = i # 遍历完后,将数组的最小值索引返回 return min_elem_index2.5 根据索引修改元素值(改)
def set(self, index, elem): """ 将索引为index的元素的值设置为elem 时间复杂度:O(1) :param index: 索引 :param elem: 新的值 """ # 判断index的合法性 if index < 0 or index >= self._size: raise Exception('Set Failed. Index is illegal.') self._data[index] = elem2.6 交换两个元素(改)
def swap(self, index1, index2): """ 交换分别位于索引index1和索引index2处的元素 时间复杂度:O(1) :param index1: 索引1 :param index2: 索引2 """ # 合法性检查 if index1 < 0 or index2 < 0 or index1 >= self._size or index2 >= self._size: raise Exception('Index is illegal') # 交换元素 self._data[index1], self._data[index2] = self._data[index2], self._data[index1] 2.7 从数组中删除元素 (删)
删除指定位置的元素,删除索引为1的元素 :




def remove(self, index): """ 删除索引为index的元素。index后面的元素都要向前移动一个位置 时间复杂度:O(n) :param index: 目标索引 :return: 位于该索引的元素的值 """ # index合法性检查 if index < 0 or index >= self._size: raise Exception('Remove Failed. Require 0 <= index < self._size') # 拷贝一下index处的元素,便于返回 ret = self._data[index] # index后面的元素都向前挪一个位置 for i in range(index, self._size - 1): self._data[i] = self._data[i + 1] # 维护self._size self._size -= 1 # 最后一个元素的垃圾回收 self._data[self._size] = None # 如果当前有效元素为总容量的四分之一且还存在有效元素, # 则将容量缩减为原来的一半 if self._size and self._capacity // self._size == 4: self._resize(self._capacity // 2) return ret有了上述的一般删除函数,也可以写出两个特殊的删除函数,分别是头部和尾部的删除函数,直接调用remove就行:
def removeFirst(self): """ 删除数组首位元素 时间复杂度:O(n) :return: 数组首位元素 """ # 直接调用remove函数 return self.remove(0) def removeLast(self): """ 删除数组末尾的元素 时间复杂度:O(1) :return: 数组末尾元素 """ # 直接调用remove函数 return self.remove(self._size - 1)2.8 根据元素值删除该元素(查+删)
其实就是调用find函数与remove函数
def removeElement(self, elem): """ 删除数组中为elem的元素,如果数组中不存在elem,那么什么都不做。 如果存在多个相同的elem,只删除最左边的那个 时间复杂度:O(n) :param elem:要删除的目标元素 """ # 尝试找到目标元素(最左边的)索引 index = self.find(elem) # elem在数组中就删除,否则什么都不做 if index != -1: # 调用remove函数 self.remove(index) def removeAllElement(self, elem): """ 删除数组内所有值为elem的元素,可以用递归来写,这里用的迭代方法。 elem不存在就什么都不做 :param elem: 要删除的目标元素 """ while True: # 循环来找elem,如果还存在就继续删除 index = self.find(elem) # 若存在 if index != -1: self.remove(index) else: break2.9 删除数组中值最大(最小)的元素(查+删)
先找出最大(最小)元素的索引,再根据该索引删除该元素
def removeMax(self): """ 删除数组中的最大元素,返回最大元素的值, 如果有多个最大值,默认值删除最左边的那个 时间复杂度:O(n) :return:最大元素 """ # 直接调用remove函数删除最大值 return self.remove(self.get_Max_index()) def removeMin(self): """ 删除数组中的最小元素,返回最小元素的值, 如果有多个最小值,默认值删除最左边的那个 时间复杂度:O(2n),可以看成是O(n)的 :return:最小元素 """ # 直接调用remove函数删除最大值 return self.remove(self.get_Max_index())三、动态数组
3.1 基本概念
即数组长度可变的数组,可以根据用户需要,有效利用存储空间。
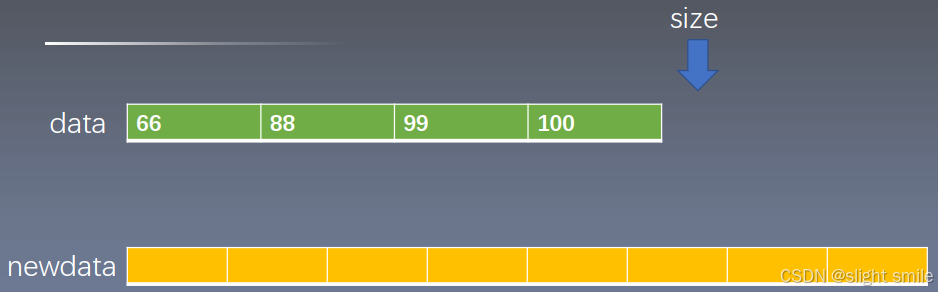
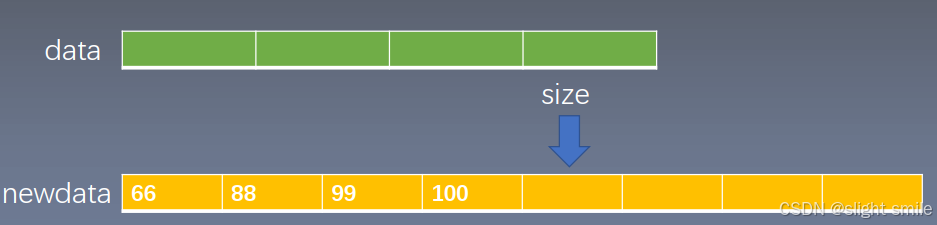
具体体现在添加元素和删除元素中,若添加元素时发现数组已经满了,则将数组长度自动扩大为原来的两倍,若删除元素后发现当前有效元素为总容量的四分之一且还存在有效元素,则将数组容量缩减至原来的一半。
add函数和remove函数中已经有所体现:
# 判断数组是否已经满了if self._size == self._capacity: # 默认扩容当前容量的二倍。容量翻倍要比容量加上一个固定值要好 # 这样做均摊复杂度为O(1),具体百度。 self._resize(self._capacity * 2) # 如果当前有效元素为总容量的四分之一且还存在有效元素,# 则将容量缩减为原来的一半if self._size and self._capacity // self._size == 4: self._resize(self._capacity // 2)再来看一下resize函数的实现:
def resize(self, new_capacity): ''' 数组容量放缩至new_capacity, :param new_capacity:新的容量 ''' # 建立一个新数组,容量为new_capacity new_arr = Arr(new_capacity) # 将当前数组的元素按当前顺序全部移动到new_arr中 for i in range(self._size): new_arr.addLast(self._data[i]) # 数组容量变为new_capacity self._capacity = new_capacity # 将new_arr._data赋值给self._data,从而完成数组的容量放缩操作 self._data = new_arr._data下面来看一下上述定义的数组类的一些基本增删改查操作:
import numpy as npnp.random.seed(7)test = Arr()print(test.getSize())print(test.getCapacity())print(test.isEmpty())for i in range(8): test.add(0, np.random.randint(5))test.printArr()test.addLast(2)test.printArr()print(test.get(3))test.set(3, 10)test.printArr()print(test.contains(10))print(test.find(4))test.findAll(1).printArr()test.remove(3)test.printArr()test.removeFirst()test.removeLast()test.printArr()test.removeElement(4)test.printArr()test.removeAllElement(3)test.printArr()for i in range(30): test.addLast(np.random.randint(10))test.printArr()print(test[3])test.swap(0, 1)test.printArr()结果如下:
010True1 0 1 4 3 3 1 4 Size: 8-----Capacity: 101 0 1 4 3 3 1 4 2 Size: 9-----Capacity: 1041 0 1 10 3 3 1 4 2 Size: 9-----Capacity: 10True70 2 6 Size: 3-----Capacity: 101 0 1 3 3 1 4 2 Size: 8-----Capacity: 100 1 3 3 1 4 Size: 6-----Capacity: 100 1 3 3 1 Size: 5-----Capacity: 100 1 1 Size: 3-----Capacity: 100 1 1 8 7 6 4 0 7 0 7 6 3 5 8 8 7 5 0 0 2 8 9 6 4 9 7 3 3 8 3 0 1 Size: 33-----Capacity: 4081 0 1 8 7 6 4 0 7 0 7 6 3 5 8 8 7 5 0 0 2 8 9 6 4 9 7 3 3 8 3 0 1 Size: 33-----Capacity: 403.2 动态数组时间复杂度分析
3.2.1 添加操作O(n)
Addlast(e) :O(1)
AddFirst(e) :O(n)
add(index,e) :O(n/2)=O(n)
最坏情况:O(n)
Resize :O(n)
3.2.2 删除操作O(n)
removelast(e): O(1)
removeFirst(e) :O(n)
remove(index,e): O(n/2)=O(n)
最坏情况:O(n)
Resize :O(n)
3.2.3 修改操作O(1)
Set(index,e) :O(1)
3.2.4 查询操作
Get(index) :O(1)
Contains(e) :O(n)
Find(e) :O(n)
3.2.5 总结
增,删 O(n)
改:已知索引O(1) 未知索引O(n)
查:已知索引O(1) 未知索引O(n)
3.3 动态数组均摊复杂度
resize复杂度分析:
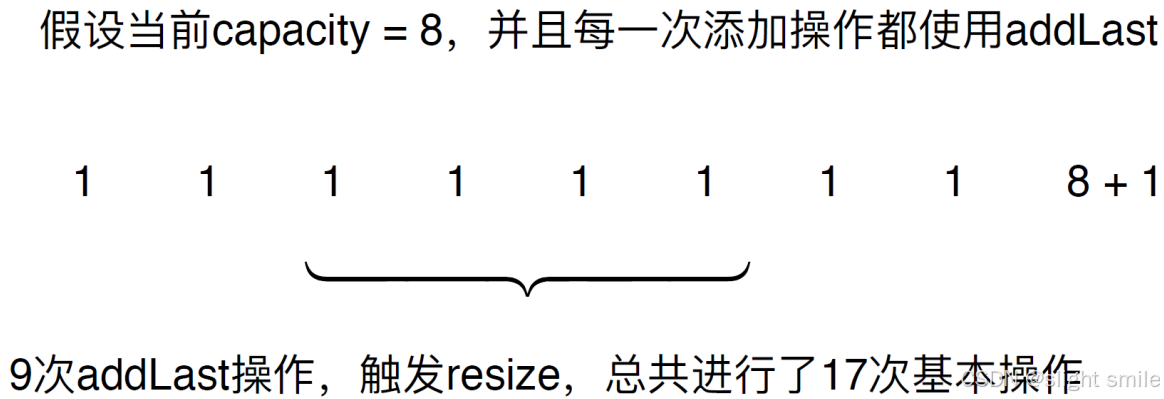
9次addlast操作,触发resize,总共进行了17次基本操作。平均,每次addlast,进行2次基本操作。
假设capacity=m, m+1次addlast,触发resize,总共进行2m+1次基本操作。平均,每次addlast,进行2次基本操作 。
均摊复杂度O(1)
3.4 Python列表与字典操作时间复杂度
3.4.1 列表操作时间复杂度
| 操作 | 操作说明 | 时间复杂度 |
|---|---|---|
| index(value) | 查找list某个元素的索引 | O(1) |
| a = index(value) | 索引赋值 | O(1) |
| append(value) | 队尾添加 | O(1) |
| pop() | 队尾删除 | O(1) |
| pop(index) | 根据索引删除某个元素 | O(n) |
| insert(index, value) | 根据索引插入某个元素 | O(n) |
| iterration | 列表迭代 | O(n) |
| contains(in) | 列表是否包含某个元素 | O(n) |
| slice[x : y] | 切片,获取x, y为O(1),获取[x : y]内的值为O(k) | O(k) |
| del slice[x : y] | 删除切片,删除后数据需要重新移动/合并 | O(n) |
| reverse | 列表翻转 | O(n) |
| sort | 排序 | O(nlogn)快排 |
3.4.2 字典操作时间复杂度
| 操作 | 操作说明 | 时间复杂度 |
|---|---|---|
| copy | 复制 | O(n) |
| get(value) | 获取 | O(1) |
| set(value) | 修改 | O(1) |
| delete(value) | 删除 | O(1) |
| contains(in) | 包含 | O(1) |
| iterration | 字典迭代 | O(n) |
因为字典的底层实现用了哈希表。