蓝桥杯真题——砍竹子（C语言）

 问题描述

这天, 小明在砍竹子, 他面前有 n 棵竹子排成一排, 一开始第 ii 棵竹子的 高度为 ​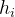.他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 H, 那么用一次魔法可以,把这一段竹子的高度都变为, 其中 [x]表示对 x 向下取整。小明想 知道他最少使用多少次魔法可让所有的竹子的高度都变为 1 。

输入格式

第一行为一个正整数 n, 表示竹子的棵数。

第二行共 n 个空格分开的正整数 ​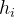, 表示每棵竹子的高度。

输出格式

一个整数表示答案。

样例输入

6

2 1 4 2 6 7

样例输出 

5

样例解释

其中一种方案：

214267

        →214262

        →214222

        →211222

        →111222

        →111111

共需要 5 步完成

评测数据规模

对于20%的数据，保证n<1000， ​<。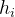

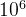对于100%的数据，保证n≤2 x ，​<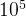

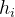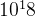
运行限制

解法代码 

#include <stdio.h>#include <stdlib.h>#include <math.h>// 定义一个二维数组来存储每个数的中间结果// 假设每个数最多经过7次操作就能降到1，所以第二维的大小设为8（索引从0到7）long long h[200001][8];// 计算给定数n经过一次操作后的结果long long sum(long long n) {    // 取当前数的一半（向下取整后加1），然后开平方根（也向下取整）    return (long long)sqrtl((long double)(n / 2 + 1));}int main(int argc, char *argv[]) {    long long n, i, j, res = 0, k;    // 读取数的数量    scanf("%lld", &n);    // 对每个数进行处理    for (i = 0; i < n; i++)     {        // 读取当前数        scanf("%lld", &h[i][0]);        // 计算当前数的所有中间值，直到该值变为1        for (j = 1; h[i][j - 1] > 1; j++)         {            h[i][j] = sum(h[i][j - 1]);            // 累加每个数所需的操作次数            res++;        }    }    // 检查相邻两个数的所有中间值，如果找到相同的中间值，则减去一次操作    for (i = 0; i < n - 1; i++)      {        for (j = 0; h[i][j] != 1; j++)        {            for (k = 0; h[i + 1][k] != 1; k++)             {                // 如果找到相同的中间值                if (h[i][j] == h[i + 1][k])                 {                    // 减去一次操作                    res--;                    // 跳出内层循环，因为已经找到了一个匹配项                    break;                }            }        }    }    // 打印出最终的结果    printf("%lld", res);    return 0;}

答案验证