【c++篇】:探秘红黑树平衡旋转原理--维持树的高度平衡之道
✨感谢您阅读本篇文章,文章内容是个人学习笔记的整理,如果哪里有误的话还请您指正噢✨
✨ 个人主页:余辉zmh–CSDN博客
✨ 文章所属专栏:c++篇–CSDN博客
文章目录
前言一.红黑树的概念和性质定义和性质节点结构与表示 二.模拟实现基本框架红黑树的插入红黑树的变色处理和平衡调整红黑树的平衡检查测试 三.完整代码文件
前言
在上一篇文章中,我们已经学习了平衡树之一的AVL树,在这篇文章中,我们将要继续学习另一个平衡树–红黑树。注意:如果想要更好地学习红黑树,建议先看一下关于二叉搜索树以及AVL树的讲解,红黑树是在这两个基础上来讲解的,有了上面两个的基础才能更好的理解和学习红黑树。
一.红黑树的概念和性质
红黑树是一种自平衡的二叉搜索树,他在计算机科学中有着广泛的应用,特别是在需要频繁插入,删除和查找的场景中。以下是关于红黑树的详细讲解:
定义和性质
红黑树是一种带有颜色属性的二叉搜索树,其中每个节点都带有红色或者黑色的颜色标志。它通过一系列的规则来确保树的平衡性,从而在插入,删除和查找操作中保持较高的效率,红黑树的性质包括:
1.每个节点要么是红色要么是黑色2.根节点是黑色3.每个叶子节点(NIL节点,在红黑树中通常表示为空节点)是黑色4.如果一个节点是红色,那他的两个子节点都是黑色,即不存在两个连续的红色节点5.从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点上面这些性质共同确保了红黑树的最长路径不会超过最短路径的二倍,从而保证了树的高度相对平衡,进而确保了插入,删除和查找操作的时间复杂度为O(log N)
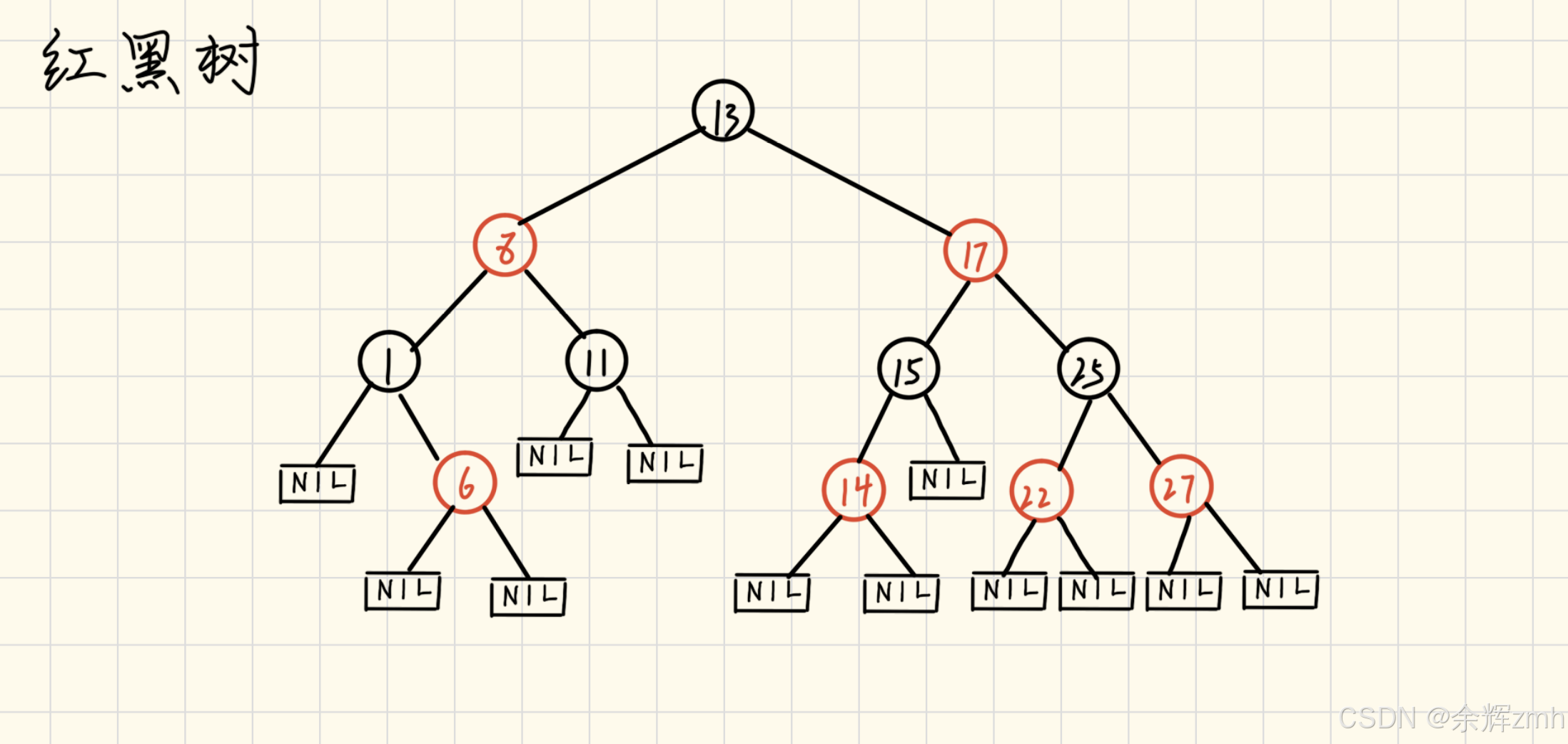
节点结构与表示
在红黑树中,每个节点通常都包含一下信息:
键值对(key,value):key值用于存储节点的值,并作为二叉搜索树的比较基值颜色(_colour):红色或者黑色,用于维护红黑树的平衡性左子节点指针(_left):指向节点的左子节点右子节点指针(_right):指向节点的右子节点父节点指针(_parent):指向节点的父节点 二.模拟实现
基本框架
代码实现:
#include<iostream>#include<utility>#include<vector>#include<time.h>using namespace std;//颜色枚举enum Colour{ RED, BLACK};//节点类封装template<class K,class V>class RBTreeNode{public: //构造函数 RBTreeNode(const pair<K,V>& kv) :_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_kv(kv) ,_col(RED) {} //成员变量 RBTree<K,V>* _left; RBTree<K,V>* _right; RBTree<K,V>* _parent; pair<K,V> _kv; Colour _col;};//红黑树类的封装template<class K,class V>class RBTree{ typedef RBTreeNode<K,V> Node;public: //构造函数 RBTree() :_root(nullptr) {} //....其他成员函数 private: //成员变量 Node* _root;};红黑树的插入
红黑树的插入和二叉搜索树的原理一样,通过基值来查找到对应的插入位置,但不同的时,在插入完后需要进行变色处理以及出现失衡时进行平衡调整,具体代码如下:
代码实现:
bool insert(const pair<K,V>& kv){ if(_root==nullptr){ _root=new Node(kv); _root->_col=BLACK; return true; } Node* parent=nullptr; Node* cur=_root; while(cur){ if(cur->_kv.first<kv.first){ parent=cur; cur=cur->_right; } else if(cur->_kv.first>kv.first){ parent=cur; cur=cur->_left; } else{ return false; } } cur=new Node(kv); cur->_col=RED; if(parent->_kv.first<kv.first){ parent->_right=cur; } else{ parent->_left=cur; } cur->_parent=parent; //变色处理以及平衡调整 //.... //插入结束后要将根节点的颜色变为黑色 _root->_col=BLACL; return true;}红黑树的变色处理和平衡调整
注意:这里只详细讲解红黑树的变色处理,以及各种平衡调整情况,关于如何旋转可以看我之前关于AVL树的文章,里面有关于旋转的详细讲解
1.parent节点在grandfather节点的左子节点
代码实现:
bool insert(const pair<int,int>& kv){ //... //插入过程 //变色处理和平衡调整 while(parent&&parent->_col=RED){ Node*grandfather=parent->_parent; //如果parent节点在grandfather节点的左子节点 if(parent==grandfather->_left){ Node* uncle=grandfather->_right; //如果uncle节点存在且节点为红色 if(uncle&&uncle->_col== RED){ //变色 parent->_col=uncle->_col=BLACK; grandfather->_col=RED; //继续往上 cur=grandfather; parent=cur->_parent; } //如果uncle节点不存在或者存在且为黑色 else{ //如果cur节点在parent节点的左子节点 if(cur=parent->_left){ //右单旋 RotateR(grandfather); //旋转后变色 grandfather->_col=RED; parent->_col=BLACK; } //如果cur节点在parent节点的右子节点 else{ //先左单旋,再右单旋 RotateL(parent); RoateR(grandfather); //旋转后变色 cur->_col=BLACK; grandfather->_col=RED; } //旋转后就是平衡了,直接结束 break; } } //如果parent节点再grandfather节点的右子节点 //.... } _root->_col=BLACK; return true;}实现原理:

2.parent节点在grandfather节点的右子节点
代码实现:
bool insert(const pair<int,int>& kv){ //... //插入过程 //变色处理和平衡调整 while(parent&&parent->_col==RED){ Node* grandfather=parent->_parent; //parent节点在grandfather节点的左子节点 //.... //parent节点在grandfather节点的右子节点 else{ Node* uncle=grandfather->_left; //如果uncle节点存在且为红色 if(uncle&&uncle->_col=RED){ //变色 parent->_col=uncle->_col=BLACK; grandfather->_col=RED; //继续往上 cur=grandfather; parent=cur->_parent; } //如果uncle节点不存在 或者 节点为黑色 else{ //如果cur节点在parent节点的右子节点 if(cur==parent->_right){ //左单旋 RotateL(grandfather); //变色 parent->_col=BLACK; grandfather->_col=RED; } //如果cur节点在parent节点的左子节点 else{ //先右单旋,再左单旋 RotateR(parent); RotateL(grandfather); //旋转后变色 cur->_colo=BLACK; grandfather->_col=RED; } break; } } } _root->_col=BLACK; return true;}实现原理:
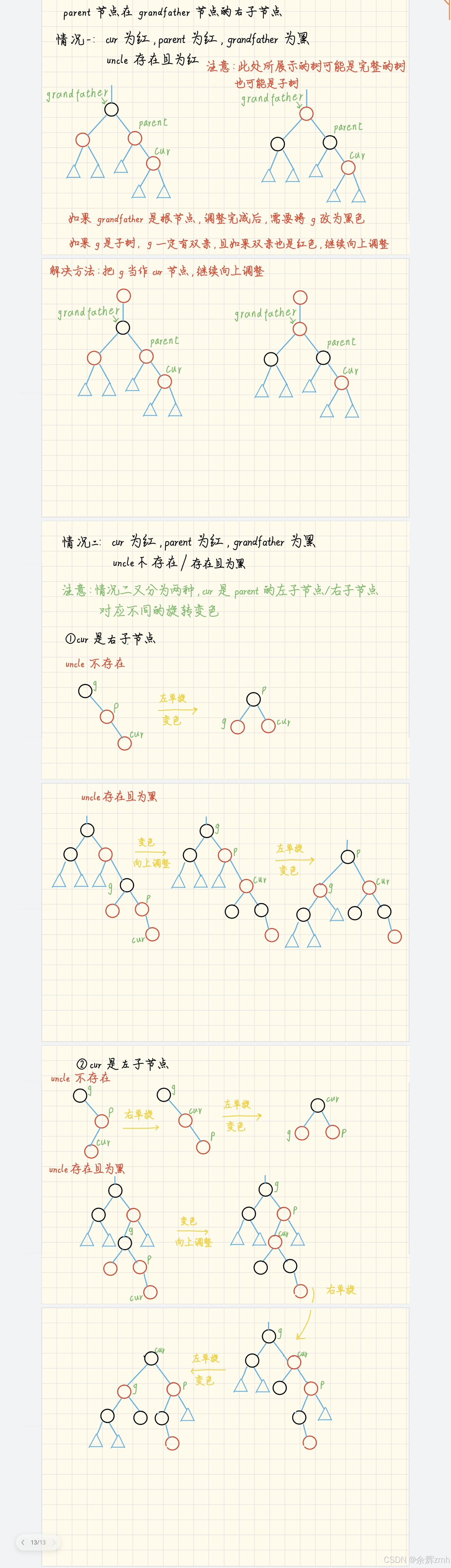
红黑树的平衡检查
代码实现://平衡检查函数bool IsBlance(){ return _IsBlance(_root);}bool CheckColour(Node* root,int blacknum,int benchmark){ //当遇到空节点时,检查该路径上黑色节点个数是否等于基准值,不等于说明出现错误 if(root==nullptr){ if(blacknum!=benchmark){ return false; } return true; } //当节点是黑色时,该路径上黑色节点个数加一 if(root->_col==BLACK){ blacknum++; } //当节点是红色时,检查父节点是否也是红色,如果是红色,说明出现连续的红色节点,出现错误 if(root->_RED&&root->_parent&&root->_parent->_col==RED){ cout<<root->_kv.first<<"RED false"<<endl; return false } //递归调用,检查左右子树 return CheckColour(root->_left,blacknum,benchmark) && CheckColour(root->_right,blacknum,benchmark);}bool _IsBlance(Node* root){ //如果是空树直接返回true if(root==nullptr){ return true; } //如果不是空树,但根节点不是黑色,出现错误 if(root->_col!=BLACK){ return false; } //设置一个基准值benchmark,从树的最左路径查找黑色节点个数作为基准值 int benchmark=0; Node* cur=root; while(cur){ if(cur->_col==BLACK){ benchmark++; } cur=cur->_left; } return CheckColour(root,0,benchmark);}AVL树一样,这里也是借用两个函数来实现平衡检查当是空树时,直接返回true,非空树时检查根节点是否是黑色,如果不是,说明出现错误之后设置一个基准值benchmark,从树的最左路径查找黑色节点个数作为基准值,调用检查函数CheckColour()检查函数中当遇到空节点时,检查该路径上黑色节点个数是否等于基准值,不等于说明出现错误当节点是黑色时,该路径上黑色节点个数加一;当节点是红色时,检查父节点是否也是红色,如果是红色,说明出现连续的红色节点,出现错误递归调用,检查左右子树 测试
测试代码:
#include"RBTree.h"//第一组数据测试void test1(){ int arr[]={16, 3, 7, 11, 9, 26, 18, 14, 15}; RBTree<int,int> t; for(auto e : arr){ t.insert(make_pair(e,e)); cout<<"Insert:"<<e<<"->"<<t.IsBlance()<<endl; }}//随机大量数据测试void test2(){ const int N=1000; vector<int> v; v.reserve(N); srand(time(0)); for(size_t i=0;i<N;i++){ v.push_back(i); } RBTree<int,int> t; for(auto e : v){ t.insert(make_pair(e,e)); } cout<<t.IsBlance()<<endl; cout<<t.Height()<<endl;}int main(){ //test1(); test2(); return 0;}测试结果:
第一组测试:
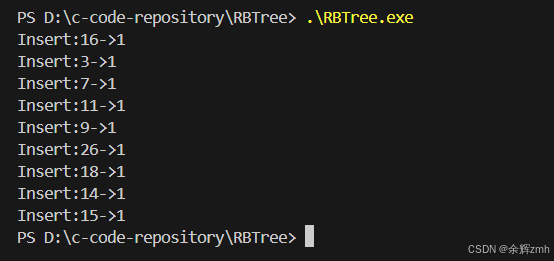
第二组测试:

三.完整代码文件
RBTree.h文件完整代码:
#include<iostream>#include<utility>#include<vector>#include<time.h>using namespace std;enum Colour { RED, BLACK};template<class K , class V>class RBTreeNode {public: //构造函数 RBTreeNode(const pair<K,V>& kv) :_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_kv(kv) ,_col(RED) {} //成员变量 RBTreeNode<K,V>* _left; RBTreeNode<K,V>* _right; RBTreeNode<K,V>* _parent; pair<K,V> _kv; Colour _col;};template<class K , class V>class RBTree { typedef RBTreeNode<K,V> Node;public: //构造函数 RBTree() :_root(nullptr) {} bool insert(const pair<K,V>& kv) { if(_root==nullptr){ _root=new Node(kv); _root->_col=BLACK; return true; } Node* parent=nullptr; Node* cur=_root; while(cur) { if(cur->_kv.first<kv.first) { parent=cur; cur=cur->_right; } else if(cur->_kv.first>kv.first) { parent=cur; cur=cur->_left; } else { return false; } } cur=new Node(kv); cur->_col=RED; if(parent->_kv.first<kv.first){ parent->_right=cur; } else{ parent->_left=cur; } cur->_parent=parent; while(parent&&parent->_col==RED){ Node* grandfather=parent->_parent; //如果parent节点在左子节点 if(parent==grandfather->_left){ Node* uncle=grandfather->_right; //如果uncle节点存在且节点为红色 if(uncle&&uncle->_col==RED){ //变色 parent->_col=uncle->_col=BLACK; grandfather->_col=RED; //继续往上 cur=grandfather; parent=cur->_parent; } //如果uncle节点不存在 或者 节点为黑色 else{ //如果cur节点在左子节点 if(cur==parent->_left){ //右单旋 RotateR(grandfather); //旋转后变色 grandfather->_col=RED; parent->_col=BLACK; } //如果cur节点在右子节点 else{ //左双旋 //先左单旋,再右单旋 RotateL(parent); RotateR(grandfather); //旋转后变色 cur->_col=BLACK; grandfather->_col=RED; } break; } } //如果parent节点在右子节点 else{ Node* uncle=grandfather->_left; //如果uncle节点存在且节点为红色 if(uncle&&uncle->_col==RED){ //变色 parent->_col=uncle->_col=BLACK; grandfather->_col=RED; //继续往上 cur=grandfather; parent=cur->_parent; } //如果uncle节点不存在 后者 节点为黑色 else{ //如果cur节点在右子节点 if(cur==parent->_right){ //左单旋 RotateL(grandfather); //变色 parent->_col=BLACK; grandfather->_col=RED; } //如果cur节点在左子节点 else{ //右双旋 //先右单旋,再左单旋 RotateR(parent); RotateL(grandfather); //旋转后变色 cur->_col=BLACK; grandfather->_col=RED; } break; } } } _root->_col=BLACK; return true; } int Height(){ return _Height(_root); } bool IsBlance(){ return _IsBlance(_root); }private: int _Height(Node* root){ if(root==nullptr){ return 0; } int leftheight=_Height(root->_left); int rightheight=_Height(root->_right); return leftheight>rightheight ? leftheight+1 : rightheight+1; } bool CheckColour(Node* root,int blacknum,int benchmark){ //如果节点是空,判断黑色节点个数是否等于基准值 if(root==nullptr){ if(blacknum!=benchmark){ return false; } return true; } //如果节点是黑色,黑色个数加加 if(root->_col==BLACK){ blacknum++; } //如果节点是红色,判断父节点是否也是红色,不能出现连续的红色节点 if(root->_col==RED&&root->_parent&&root->_parent->_col==RED){ cout<<root->_kv.first<<"RED False"<<endl; return false; } return CheckColour(root->_left,blacknum,benchmark) &&CheckColour(root->_right,blacknum,benchmark); } bool _IsBlance(Node* root){ if(root==nullptr){ return true; } //如果根节点不是黑色,返回错误 if(root->_col!=BLACK){ return false; } //设置一个基准值 int benchmark=0; Node* cur=root; while(cur){ if(cur->_col==BLACK){ benchmark++; } cur=cur->_left; } return CheckColour(root,0,benchmark); } //左单旋 void RotateL(Node* parent){ Node* cur=parent->_right; Node* curleft=cur->_left; Node* ppnode=parent->_parent; parent->_right=curleft; if(curleft){ curleft->_parent=parent; } cur->_left=parent; parent->_parent=cur; if(ppnode){ if(ppnode->_left==parent){ ppnode->_left=cur; cur->_parent=ppnode; } else{ ppnode->_right=cur; cur->_parent=ppnode; } } else{ cur->_parent=nullptr; _root=cur; } } //右单旋 void RotateR(Node* parent){ Node* cur=parent->_left; Node* curright=cur->_right; Node* ppnode=parent->_parent; parent->_left=curright; if(curright){ curright->_parent=parent; } cur->_right=parent; parent->_parent=cur; if(ppnode){ if(ppnode->_left==parent){ ppnode->_left=cur; cur->_parent=ppnode; } else{ ppnode->_right=cur; cur->_parent=ppnode; } } else{ cur->_parent=nullptr; _root=cur; } }private: Node* _root;};以上就是关于平衡树之一的红黑树平衡原理讲解,如果哪里有错的话,可以在评论区指正,也欢迎大家一起讨论学习,如果对你的学习有帮助的话,点点赞关注支持一下吧!!!


登录后可发表评论
点击登录