
文章目录
哈希概念一、直接定址法二、哈希冲突1. 哈希冲突概念引入2. 除留余数法(值的分布范围分散)3. 存在哈希冲突(闭散列-开放定址法) 三、删除与查找数据1. 删除与查找数据存在的问题2. 状态标记 四、什么时候扩容?1. 哈希表效率问题2. 负载因子 五、哈希表框架搭建六、开放定址法代码实现——插入1. 线性探测实现2. 插入扩容逻辑3. key不能取模的问题默认缺省整形的处理string的特化仿函数的使用 七、开放定址法代码实现——查找八、开放定址法代码实现——删除代码总结与运行结果
哈希概念
哈希(hash)又称散列,是⼀种组织数据的方式。从译名来看,有散乱排列的意思。本质就是通过哈希
函数把关键字Key跟存储位置建立⼀个映射关系,查找时通过这个哈希函数计算出Key存储的位置,进行快速查找。
一、直接定址法
当关键字的范围比较集中时,直接定址法就是非常简单高效的方法:
比如一组关键字都在 [0,99] 之间,那么我们开一个 100 个数的数组,每个关键字的值直接就是存储位置的下标。再比如一组关键字值都在 [a,z] 的小写字母,那么我们开一个 26 个数的数组,每个关键字的 ASCII 码减去 ‘a’ 的 ASCII 码就是存储位置的下标。也就是说,直接定址法本质就是用关键字计算出一个绝对位置或者相对位置。
小试??:
387. 字符串中的第⼀个唯⼀字符 - 力扣(LeetCode)

class Solution {public: int firstUniqChar(string s) { int arr[26] = {0}; for(auto e : s) { arr[e - 'a']++; } for(int i = 0; i < s.size(); i++) { if(arr[s[i] - 'a'] == 1) return i; } return -1; }};二、哈希冲突
1. 哈希冲突概念引入
直接定址法的缺点也非常明显:
当关键字的范围比较分散时,会造成内存浪费,甚至内存不足的情况。
假设我们只有数据范围是 [0, 9999] 的 N 个值,但需要将它们映射到一个大小为 M 的数组中(一般情况下 M >= N),
就需要借助哈希函数(hash function,简称 hf)。关键字 key 被放到数组的 h(key) 位置。
注意:h(key) 计算出的值必须在 [0, M) 之间。
存在的问题:
哈希冲突两个不同的 key 可能会映射到同一个位置,这种情况叫做哈希冲突或哈希碰撞。优化方向
理想情况下,我们希望找到一个好的哈希函数以避免冲突,但实际上冲突是不可避免的。
因此需要尽可能设计优秀的哈希函数来减少冲突次数,同时设计出有效的冲突解决方案。
2. 除留余数法(值的分布范围分散)
除留余数法就可以去解决上述值比较分散的问题:
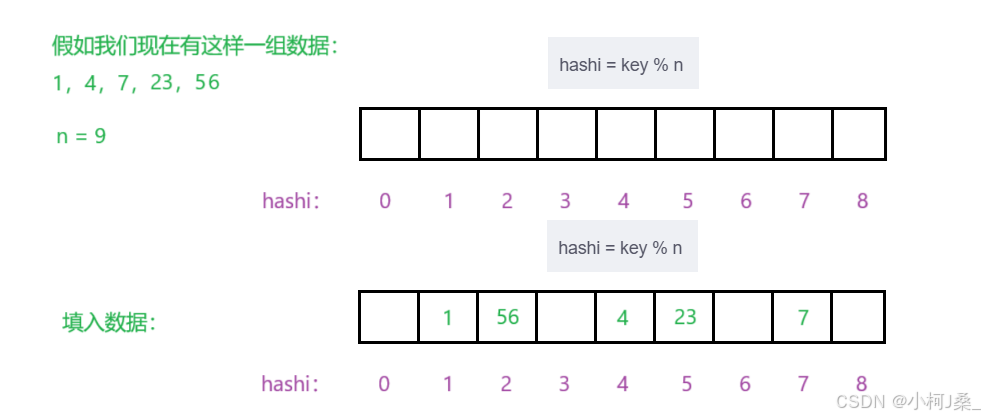
hashi = key % n
如下图:
3. 存在哈希冲突(闭散列-开放定址法)
上述方法是会出现哈希冲突的,比如要插入40,而·40 % 9 = 4,但是 4 这个位置已经有数据 4 了,因此就会发生哈希冲突。
解决哈希冲突:
闭散列-开放定址法,即:当前位置被占用了,按规则找下一个位置(占用别人的位置)
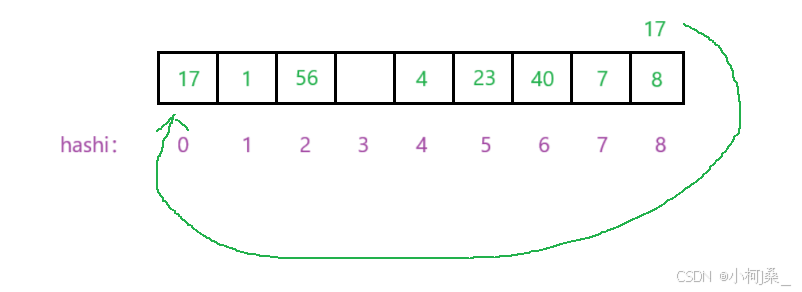
这里我们先用 1. 线性探测
还是上述的例子,比如要在当前环境下插入40:
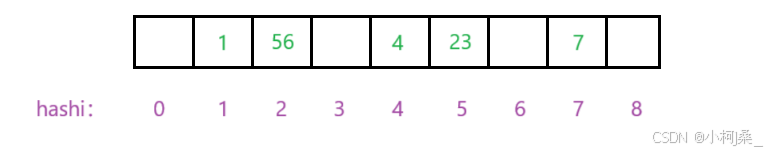
存在冲突:
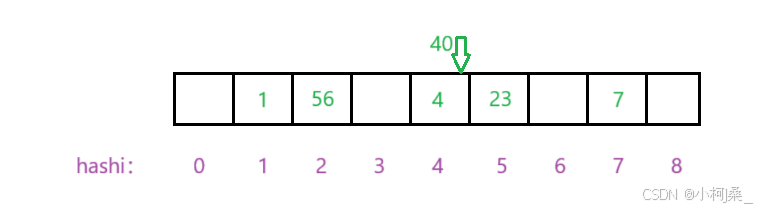
按照顺序继续向后找,直到遇到可以插入的位置:
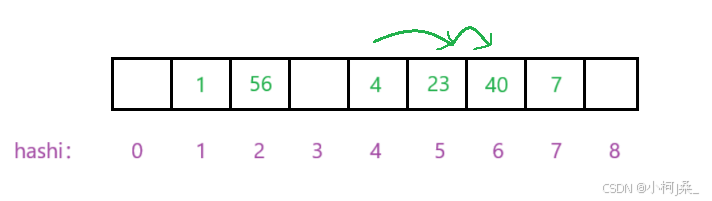
同理,我们要插入8,再插入17
三、删除与查找数据
1. 删除与查找数据存在的问题
查找数据:从data % n的位置开始查找,不为空就继续向后找,为空就停止。

2. 状态标记
如何解决上述的问题呢?
使用状态标记:
enum STATE // 状态标记
{
EXIST // 存在
DELETE // 删除
EMPTY // 空
}
每当我们删除了一个数据以后,就像该位置的数据改为 DELETE,而 DELETE 状态的数据不算在有效数据以内,查找的时候遇到该状态不停止,遇到空才停止。
而当我们新插入数据是,DELETE和EMPTY位置都可以插入数据。
这样就解决了删除和查找的问题。
四、什么时候扩容?
1. 哈希表效率问题
通过上述的观察,我们可以发现,在数据比较少的时候,不论是插入删除还是查找,我们很容易就遇到空,但是一旦数据比较到,遇到哈希冲突了之后就需要一直向后找空位置,在数据将近满了之后,查找的时间复杂度基本上就是O(n),而不在是常数级别了。
因此,每当数据达到一定数量的时候,就需要扩容!
那么如何扩容呢?
2. 负载因子
如何解决上述问题呢?
提供负载因子
假设哈希表中已经映射存储了 N 个值,哈希表的大小为 M,那么负载因子N / M(有些地方也翻译为载荷因子/装载因子等,其英文为 load factor)定义如下:
这⾥我们哈希表负载因子控制在0.7,当负载因子到0.7以后我们就需要扩容了。
五、哈希表框架搭建
接下来我们开始搭建哈希表~
#pragma once#include<vector>enum STATE{EXIST, // 存在EMPTY, // 空DELETE // 删除};template<class K, class V>struct HashData{pair<K, V> _kv;STATE _state = EMPTY; // 初始状态为空};template<class K, class V>class HashTable{public:HashTable(){_table.resize(10); }private:vector<HashData<K, V>> _table;size_t _n = 0; // 存储有效数据的个数};六、开放定址法代码实现——插入
1. 线性探测实现
这有一个要注意的点,线性探测时我们计算hashi时Key除的是capacity还是size?
答:除以size,因为我们后面要通过[ ]进行访问,而[ ]会进行assert()是否越界越size,如果除capacity,就会造成越界。
bool Insert(const pair<K, V>& kv){// 扩容// ... //// 线形探测size_t hashi = kv.first % _table.size();while (_table[hashi]._state == EMPTY){++hashi;hashi %= _table.size();}_table[hashi]._state = EXIST;_table[hashi]._kv = kv;++_n;return true;}2. 插入扩容逻辑
扩容这里有几个需要输入的点:
遍历旧表的时候,数据映射关系被改变了,因此要重新插入数据。
我们这里的逻辑是直接复用插入本身这个函数(也就是复用线性探测的逻辑),这里是不会出现死循环的,因为进入 if 判断条件就会扩容,也就是扩容了才会复用,而复用时因为已经扩容了所以不会循环下去。
新表的 _table 创建好了之后,直接利用swap进行交换就可以了,旧表伴随Insert栈帧的结束会自动释放。
// 扩容if ((double)_n / _table.size() >= 0.7){size_t newsize = _table.size() * 2;// 重新建立一个新表HashTable<K, V> newtable;newtable._table.resize(newsize);// 遍历旧表,将数据放到新表中去for (size_t i = 0; i < _table.size(); i++){if (_table[i]._state == EXIST){newtable.Insert(_table[i]._kv);}}_table.swap(newtable._table);}3. key不能取模的问题
当 key 是 string / Date 等类型时,key 不能直接取模,因此我们需要给 HashTable 增加一个仿函数。这个仿函数支持将 key 转换成一个可以取模的整数。如果 key 可以转换为整数并且不容易发生冲突,那么这个仿函数可以使用默认参数;如果这个 key 不能直接转换为整数,我们就需要自己实现一个仿函数并传给这个参数。
实现这个仿函数的要求是,尽量让 key 的每个值都参与到计算中,从而使得不同的 key 转换出的整数值尽可能不同。
string 作为哈希表的 key 非常常见,因此我们可以考虑对 string 类型进行特化处理。
// 多加一种仿函数进行控制template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable缺省参数给DefaultHashFunc< K>,它的作用是——我们默认是整形,他会返回对应的无符号整型值。
这样的好处是,如果我们传过来的是负数,也可以正常取模进行操作~
默认缺省整形的处理
template<class K>struct DefaultHashFunc{size_t operator() (const K& key){return (size_t)key;}};string的特化
因为string是一种常用的类,因此这里我们把它写成特化,对于string类怎么取出对应的数进行取模运算,还要减少冲突,有许多的大佬对这里的算法进行实现:
在哈希表中,字符串转整形是一个核心问题。为了高效地将字符串映射到整数,常用的哈希算法有几种,每种方法都具有不同的性能特点,特别是在哈希冲突的处理上。以下是几种常见的哈希算法及其基本思路:
常见的哈希算法和思路:

性能对比表格:
| 哈希算法 | 冲突概率 | 计算复杂度 | 适用场景 | 优势 | 缺点 |
|---|---|---|---|---|---|
| BKDR Hash | 中等 | O(n) | 小型字符串 | 简单、高效,适合短字符串和小哈希表 | 对大字符串可能存在较多冲突 |
| SDBM Hash | 较低 | O(n) | 字符串查找 | 较少冲突,常用于文件查找 | 较为简单,可能在某些场景下效率较低 |
| DJB2 Hash | 较低 | O(n) | 字符串查找 | 高效、低冲突,广泛应用 | 对长字符串的处理可能不如 MurmurHash |
| FNV-1a Hash | 非常低 | O(n) | 高效字符串查找 | 良好的分布性和抗碰撞能力 | 比其他方法略慢,适用于不需要极端效率的场景 |
| MurmurHash | 极低 | O(n) | 大型数据处理 | 非常高效、抗碰撞能力强 | 实现较复杂,计算开销较大 |
这里我们用BKDR的方法实现string的特化
template<>struct DefaultHashFunc<string>{size_t operator() (const string& str){// BKDRsize_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}};仿函数的使用
这里使用仿函数的时候包一层就可以了~
// 仿函数控制HashFunc hf;size_t hashi = hf(kv.first) % _table.size();七、开放定址法代码实现——查找
查找这里同样使用的是线性探测,如果不为空就一直向后查找,如果找到了并且状态为存在就返回。哈希表的数据不能轻易修改,因此我们返回的时候要返回HashData<const K, V>*,因为Key是不能i修改的,因此这里返回的时候最好也强转以下,增强代码可读性与健壮性。 HashData<const K, V>* Find(const K& key){// 线性探测HashFunc hf;size_t hashi = hf(key) % _table.size();while (_table[hashi]._state != EMPTY ){if (_table[hashi]._state == EXIST&& _table[hashi]._kv.first == key){return (HashData<const K, V>*) & _table[hashi];}++hashi;hashi %= _table.size();}return nullptr;}八、开放定址法代码实现——删除
删除复用Find就好,如果找到了就将其状态设置为DELETE。
bool Erase(const K& key){HashData<const K, V>* ret = Find(key);if (ret){ret->_state = DELETE;--_n;return true;}return false;}代码总结与运行结果
// HashTable.h#pragma once#include<vector>enum STATE{EXIST, // 存在EMPTY, // 空DELETE // 删除};template<class K, class V>struct HashData{pair<K, V> _kv;STATE _state = EMPTY; // 初始状态为空};template<class K>struct DefaultHashFunc{size_t operator() (const K& key){return (size_t)key;}};template<>struct DefaultHashFunc<string>{size_t operator() (const string& str){// BKDRsize_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{public:HashTable(){_table.resize(10); }bool Insert(const pair<K, V>& kv){// 扩容if ((double)_n / _table.size() >= 0.7){size_t newsize = _table.size() * 2;// 重新建立一个新表HashTable<K, V> newtable;newtable._table.resize(newsize);// 遍历旧表,将数据放到新表中去for (size_t i = 0; i < _table.size(); i++){if (_table[i]._state == EXIST){newtable.Insert(_table[i]._kv);}}_table.swap(newtable._table);}// 线形探测// 仿函数控制HashFunc hf;size_t hashi = hf(kv.first) % _table.size();while (_table[hashi]._state == EXIST){++hashi;hashi %= _table.size();}_table[hashi]._state = EXIST;_table[hashi]._kv = kv;++_n;return true;}HashData<const K, V>* Find(const K& key){// 线性探测HashFunc hf;size_t hashi = hf(key) % _table.size();while (_table[hashi]._state != EMPTY ){if (_table[hashi]._state == EXIST&& _table[hashi]._kv.first == key){return (HashData<const K, V>*) & _table[hashi];}++hashi;hashi %= _table.size();}return nullptr;}bool Erase(const K& key){HashData<const K, V>* ret = Find(key);if (ret){ret->_state = DELETE;--_n;return true;}return false;}private:vector<HashData<K, V>> _table;size_t _n = 0; // 存储有效数据的个数};//test.cpp#include<iostream>using namespace std;#include"HashTable.h"int main(){HashTable<int, int> ht;int a[] = { 1,111,4,7,15,25,44,9 };for (auto e : a){ht.Insert(make_pair(e, e));}ht.Erase(15);auto ret = ht.Find(4);//ret->_kv.first = 41;ret->_kv.second = 400;//HashTable<string, string, StringHashFunc> dict;HashTable<string, string> dict;dict.Insert(make_pair("sort", "排序"));dict.Insert(make_pair("left", "xxx"));auto dret = dict.Find("left");//dret->_kv.first = "xx";dret->_kv.second = "左边";string s1("xxx");string s2("xxx");DefaultHashFunc<string> hf;cout << hf(s1) << endl;cout << hf(s2) << endl;cout << hf("bacd") << endl;cout << hf("abcd") << endl;cout << hf("abbe") << endl;cout << hf("https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&rsv_idx=1&tn=65081411_1_oem_dg&wd=STATE&fenlei=256&rsv_pq=0xdd48647300054f47&rsv_t=1cd5rO%2BE6TJzo6qf9QKcibznhQ9J3lFwGEzmkc0Goazr3HuQSIIc2zD78Pt0&rqlang=en&rsv_enter=1&rsv_dl=tb&rsv_sug3=2&rsv_n=2&rsv_sug1=1&rsv_sug7=100&rsv_sug2=0&rsv_btype=i&prefixsug=STAT%2526gt%253B&rsp=5&inputT=656&rsv_sug4=796") << endl;return 0;}运行结果如下:
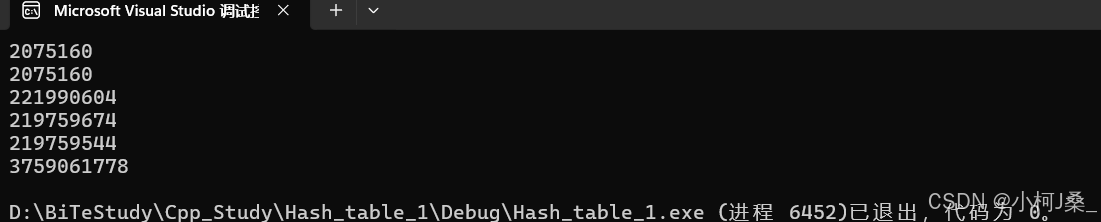
到这里就结束啦~
创作不易,求求各位观众老爷一个一键三连,谢谢大家~
