1、人工智能
内涵和外延
英文:Artificial Intelligence
定义
- 能力方面:人工智能就是用人工的方法在机器(计算机)上实现的智能,或称机器智能。
- 学科方面:是一门研究如何构造智能机器或智能系统,以模拟、延申和扩展人类智能的学科
非PPT内容:来自李德毅院士,仅供参考
内涵:包括脑认知基础、机器感知与模式识别、自然语言处理与理解、知识工程这四个方面。
外延:是机器人与智能系统——智能科学的应用技术 。这包括工业机器人、农业机器人、服务机器人等各类机器人以及智能交通、智能制造、智慧医疗、智慧城市等等。
2、知识表示方法
典型的知识表示方法
一阶谓词逻辑表示法 (PPT 2-0 38)
基本思想:一种重要的知识表示方法,它以数理逻辑为基础,是到目前为止能够表达人类思维和推理的一种最精确的形式语言。它的表现方式和人类自然语言非常接近,它能够被计算机作精确推理
举个例子 ( ∀ x ) ( ∃ y ) ( P E R S O N ( x ) → H A S F A T H E R ( x , y ) ) (\forall x)(\exists y)(PERSON(x) \rightarrow HASFATHER(x,y)) (∀x)(∃y)(PERSON(x)→HASFATHER(x,y))表示每个人(x)都有一个父亲(y)
全过程
- 用谓词演算将问题形式化。
- 在这种逻辑表示的形式上建立控制系统。
- 证明从初始状态可以达到目标状态。
优点
- 符号简单,描述易于理解
- 自然、严密、灵活、模块化
- 具有严格的形式定义
- 每项事实仅需表示一次
- 具有证明过程中所使用的推理规则
- 利用定理证明技术可从旧事实推出新事实
缺点
- 难于表示过程式和启发式知识
- 由于缺乏组织原则,利用该方法表示的知识库难于管理
- 由于是弱证明过程,当事实的数目增大时,在证明过程中决定使用哪条规则时可能产生组合爆炸
- 不具有表示不精确和不确定知识的能力
产生式表示法(规则表示法)(PPT 2-0 45)
**描述:**一组产生式在一起互相配合,协同作用,一个产生式生成的结论可以作为另一个产生式的前提,以获得问题的解决,这样的系统为产生式系统。
举个例子:IF 动物是哺乳动物 AND 吃肉 THEN 该动物是食肉动物
分类
- 按推理方向
- 前向推理:从事实到结论
- 后向推理:从目标求事实
- 双向推理:双向直到某个中间界面上两方向结果相符
- 按组织结构
- 可交换产生式系统:规则次序可交换
- 可分解产生式系统:复杂问题可分解
- 可恢复产生式系统:出现困难可撤销
优点
- 格式固定,形式单一,规则(知识单位)间相互较为独立,没有直接关系,使数据库的建立较为容易,处理较为简单的问题是可取的
- 推理方式单纯。特别是知识库与推理机是分离的,这种结构给知识库的修改带来方便,对系统的推理路径也容易做出解释
- 既可以表示确定性知识又可以表示不确定性知识,既便于表示启发性知识又便于表达过程性知识
- 既可以表示确定性知识又可以表示不确定性知识,既便于表示启发性知识又便于表达过程性知识
缺点
- 由于规则库一般都比较庞大,匹配通常是十分耗时的,这样系统的工作效率就受到影响
- 在求解复杂问题时还容易引起组合爆炸
- 适合表达具有因果关系的过程性知识,对于具有结构关系的知识无能为力
语义网络表示法
**描述:**语义网络利用结点和带标记的边构成的有向图描述事件、概念、状况、动作以及客体之间的关系。带标记的有向图能十分自然的描述客体之间的关系。
**构成:**语法、结构、过程和语义
可以很容易转化为Prolog语言,举几个例子
color(red) :红色
father_of(zzj, hht) :zzj是hht的父亲
is_a(red, color) :红色是一种颜色
优点:结构性、联想性、自索引性、自然性
缺点:非严格性、复杂性
优点
- 重要相关性能被明确地清晰地表示出来
- 基于联想记忆模型,相关事实可以从其直接相连的结点中推导出来,而不必遍历整个庞大的知识库,从而避免了组合爆炸
- 具有继承性,并易于对继承层次进行演绎
- 能够利用少量的基本概念的记号建立状态和动作的描述
缺点
- 不能保证网络操作所得结沦的有效性
- 逻辑表达不充分,无法嵌入启发式信息
- 对于网络不存在标准的术语和约定,语义解释取决于操作网络的程序
- 网络的搜索需要强有力的组织原则
框架表示法 (PPT 2-0 88)
描述:框架表示法是以框架理论为基础发展起来的一种结构化的知识表示,它适用于表达多种类型的知识。
例 下面是一个描述“大学教师”的框架:
框架名:<大学教师>
类属:<教师>
学位:(学士,硕士,博士)
专业:<学科专业>
职称:(助教,讲师,副教授,教授)
外语:语种:范围:(英,法,日,俄,德,…)
缺省:英
水平:(优,良,中,差)
缺省:良
求解问题的基本过程:
- 将问题用适当的框架表示出来。
- 与数据库中已有的框架进行匹配。
- 确定可匹配的预选框架,收集进一步信息。
- 选用适当的评价方法对预选框架进行评价,决定其是否被接受。
将框架用prolog进行表示:
frame(name("教师")),
kind_of("<知识分子>"),
work(scope("教学","科研"),default("教学")),
sex("男","女"),
reco_of_f_s("中师","高师"),
type("<小学教师>","<中学教师>","<大学教师>").
优点
- 结构性:表示知识内部结构关系和知识间特殊联系
- 深层性:多方面、多属性、分层表示知识
- 继承性:继承上层槽值
- 自然性:易于理解
缺点
- 缺乏框架的形式理论
- 缺乏过程性知识表示
- 清晰性难以保证
适用领域
- 表述数学概念及相对较窄的专业知识领域
脚本表示法 (PPT 2-0 105)
描述:脚本与框架类似,由一组槽组成,用来表示特定领域内一些事件的发生序列。
**基本思想:**把人类生活中各类故事情节的基本概念抽取出来,构成一组原子概念,确定这些原子概念间的相互依赖关系,然后把所有故事情节都用这组原子概念及其依赖关系表示出来。
脚本通常由开场条件、角色、 道具、场景和结局等几部分组成。
关于组成,举个例子:
(1) 进入条件:① 顾客饿了,需要进餐;② 顾客有足够的钱。
(2) 角色:顾客,服务员,厨师,老板。
(3) 道具:食品,桌子,菜单,钱。
(4) 场景:
场景1:进入—— ① 顾客进入餐厅;② 寻找桌子;③ 在桌子旁坐下。
场景2:点菜—— ① 服务员给顾客菜单;② 顾客点菜;③ 顾客把菜单还给服务员;④ 顾客等待服务员送菜。
场景3:等待—— ① 服务员告诉厨师顾客所点的菜;②厨师做菜,顾客等待。
场景4:吃饭—— ① 厨师把做好的荣给服务员;② 服务员把菜送给顾客;③ 顾客吃菜。
场景5:离开—— ① 服务员拿来账单;② 顾客付钱给服务员;③ 顾客离开餐厅。
(5) 结果:① 顾客吃了饭,不饿了;② 顾客花了钱;③ 老板赚了钱;④ 餐厅食品少了。
关于推理,举个例子
“昨晚,何雨到了餐厅,他订了鱼香肉丝、大米。当他要付款时发现没钱了。因为开始下雨了,所以他赶快回家了”
如果有人问:
“昨晚,何雨吃饭了吗?”
虽然在上面没有提到何雨吃没吃饭的问题,但借助于餐厅剧本,可以回答:“他吃了”。这是因为启用了餐厅剧本。情节中的所有事件与剧本中所预测的事件序列相对应,因为可以推出整个事件正常进行时所得出的结果。
应用领域
- 主要在自然语言理解方面获得了一些应用
过程表示法(PPT 2-0 116)
举个例子:如果x与y是同班同学,且z是x的老师,则z也是y的老师
BR(Teacher? z? y)
GOAL(Classmate? x y)
GOAL(Teacher z x)
INSERT(Teacher z y)
RETURN
/*
其中
BR是逆向推理标志;
GOAL表示求解子目标,即进行过程调用;
INSERT表示对数据库进行插入操作;
RETURN作为结束标志;
带"?"的变量表示其值将在该过程中求得。
*/
组成
- 激发条件
- 演绎操作
- 状态转换
- 返回
问题求解基本过程
- 每当有一个新的目标时,就从可以匹配的过程规则中选择一个执行之。在该规则的执行过程中可能会产生新的目标,此时就调用相应的过程规则并执行它。
优点
- 表示效率高
- 控制系统容易实现
缺点
- 不易修改和添加新知识
- 对某一过程进行修改时,可能印象到其他过程,对系统的维护带来不便
Petri网表示法 (PPT 2-0 127)
组成:位置、转换和标记
基本思想:用不同的位置来代表产生式规则的前提及结论,用转换来表示不同的规则强度,从而实现Petri网对产生式规则的规则集的映射。
**表示形式:**8元组
(P,T,D,I,O,f,α,β)
/*
其中:
P是位置的有限集,记为P={p1,p2,…,pn};
T是转换的有限集,记为T= {t1,t2,…,tn} ;
D是命题的有限集,记为D= {d1,d2,…,dn} ;
I是输入函数,表示从位置到转换的映射;
O是输出函数,表示从转换到位置的映射;
F是相关函数,表示从转换到0~1之间一个实数的映射,表示规则强度;
α是相关函数,表示从转换到0~1之间一个实数的映射,表示位置对应命题的可信度;
β是相关函数,表示从位置到命题的映射,表示位置所对应的命题。
*/
可信度:用[0,1]上一个实数表示,值越大表示相信为真的程度越高
对于一个产生式规则,其可信度称为强度规则
特点
- 便于描述系统状态的变化及对系统特性的分析
- 可在不同层次上变换描述,不必注意细节及相应的物理表示
- 适用于表述不确定性知识
面向对象表示法 (PPT 2-0 135)
基本特点
- 模块性
- 封装性
- 继承性
- 多态性
- 易维护性
表示方法
class <类名> [:<父类名>]
{
private :
<私有成员>
public :
<公有成员>
}
主要特点
- 继承性
- 灵活
- 易于维护
- 可重用性好
- 等等
状态空间表示法 (PPT 2-0 147)
描述:状态空间表示法是基于解答空间的问题表示和求解方法。
三元状态(S,F,G)
- 所有可能的问题初始状态集合S、操作符集合F以及目标状态集合G
过程
- 准备:描述初始状态,确定操作符集合,描述目标状态特性。
- 求解:从初始状态出发,每次加一个操作符产生新的状态描述,并递增地建立起操作符的相应实验序列,直至达到目标状态为止。
- 检验:对于求解过程中产生的新状态进行查看,确定其是否与目标状态描述相匹配。相对于最优化问题还要寻求某一准则下的最优化路径。
优点
- 思路简单,清晰明确,操作简便
缺点
- 由于它需要扩展节点,当解决复杂问题时就容易产生“组合爆炸”
适用范围
- 求解简单问题
问题归约表示法 (PPT 2-0 151)
**基本思想:**从目标出发进行逆向推理,通过一系列变换把初始问题变换为子问题集合和子—子问题集合,直至最后归约为一个平凡的本原问题集合。这些本原问题的解可以直接得到,从而解决了初始问题。
比较
- 产生式表示法与逻辑表示法。产生式表示法的主要思想是基于产生式的,其描述形式与逻辑蕴含式十分相似。如前所述,逻辑蕴含式只是产生式的一种特殊形式。然而产生式表示法较之逻辑表示法却有一个突出的优势,就是可以表示不确定性知识,因此它就具有更加广泛的应用。
- 产生式表示法与过程表示法。产生式系统也可以看成是一种过程表示方式。两者的主要区别在于:子程序表示允许子程序之间可以直接通信;而在产生式系统中,产生式规则只能通过全局数据库互相作用。
- 产生式表示法与框架表示法。产生式表示法主要用于描述事物之间的因果关系,而框架表示法则主要用于描述事物的内部结构以及事物之间的类属关系。
- **脚本结构与框架结构。**脚本结构与框架结构相比,要呆板得多,知识表示的范围也比较窄。因此,脚本无法有效表示生活当中多种多样的知识。但是,对于表达预先构思好的特定知识或顺序性动作及事件,如理解故事情节等,是非常有效的。
- 过程表示法与说明性表示方法。
- 优点
- 有利于启发式知识
- 能实现扩充逻辑的推理(如缺省推理等)
- 具有高度模块化的优点
- 能够通过类比进行推理
- 缺点
- 由于知识隐含在过程之中,因此难于修改和维护
- 固定的控制信息限定了其他可能的方法
- 优点
3、图搜索
图搜索算法过程,包括与或图
状态图搜索(PPT 3-2 41)
-
搜索:从初始节点出发,沿着与之相连的边试探地前进,寻找目标节点的过程。
-
搜索过程中经过的节点和边,按原图的连接关系,便会构成一个树型的有向图,这种树型有向图称为搜索树。
-
搜索进行中,搜索树会不断增长,直到当搜索树中出现目标节点,搜索便停止。这时从搜索树中就可很容易地找出从初始节点到目标节点的路径(解)来。
ClOSED表动态数据结构用来记录考察过的节点。
OPEN表的动态数据结构用来登记当前待考查的节点。
树式搜索算法
-
把初始节点S0放入OPEN表中。
-
若OPEN表为空,则搜索失败,退出。
-
取OPEN表中第一个节点N放在CLOSED表中;并冠以顺序编号n;
-
若目标节点Sg=N,成功退出。
-
若N不可扩展,转步2。
-
扩展N,生成一组节点,对这组子节点作如下处理:
- 删除N的先辈节点(如果有的话)。
- 对于已存在于OPEN表中的节点(如果有的话)也删除之;删除之前要比较其返回初始节点的新路径与原路径,如果新路径“短”,则修改这些节点在OPEN表中的原返回指针,使其沿新路径返回。
- 对已存在于CLOSED表的节点,作与(2)同样的处理,并且将其移出CLOSED表,放入OPEN表中重新扩展。
- 对其余子节点配上指向N的返回指针后放入OPEN表中某处,或对OPEN表进行重新排序,转步2。
零零散散的算法(深度、广度、穷举、启发、加权等)太多了,看PPT吧,但基本的思想都差不多。
h(x)启发函数
全局择优:每次找open表中全部节点里代价最小的那个进行扩展,并加入子节点
局部择优:每次只找子节点中代价最小的节点进行扩展
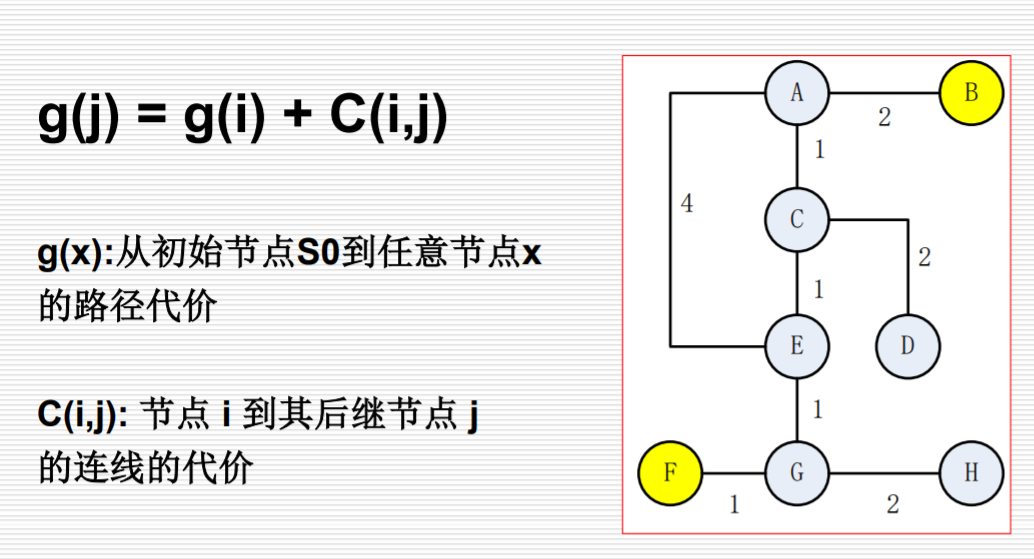
g(x)代价函数
分支限界法:每次只扩展权值最小的
最近择优法:每次只扩展子节点中权值最小的
A算法
f(x) = h(x) + g(x) :
A*算法
在A算法的基础上要求h(x)<=h*(x)
(其中h*(x)是节点x到目标节点的最小代价)
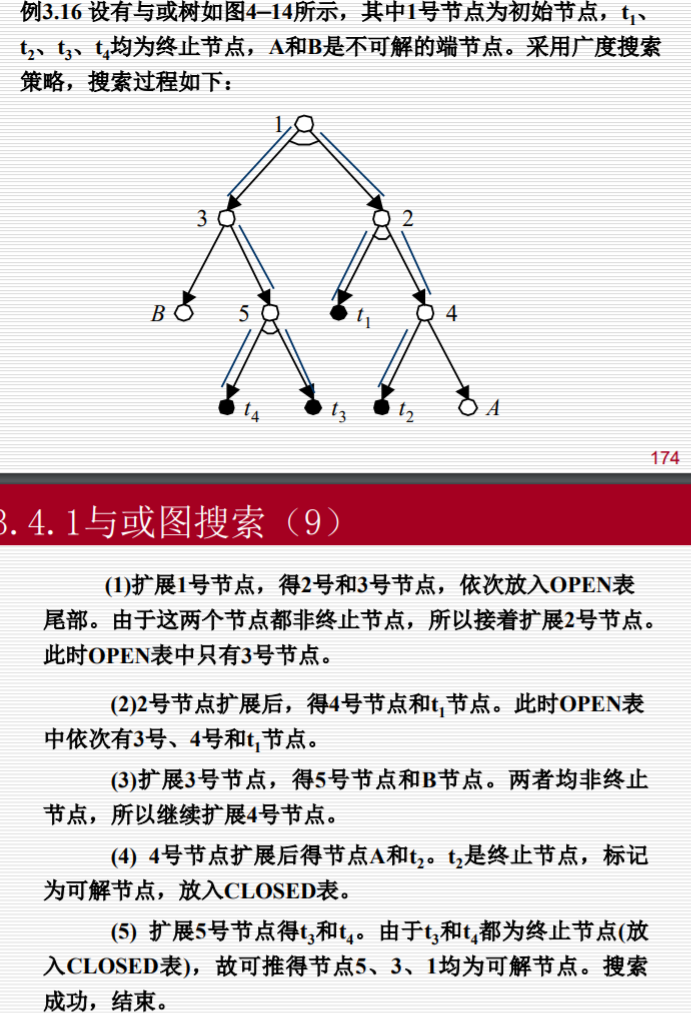
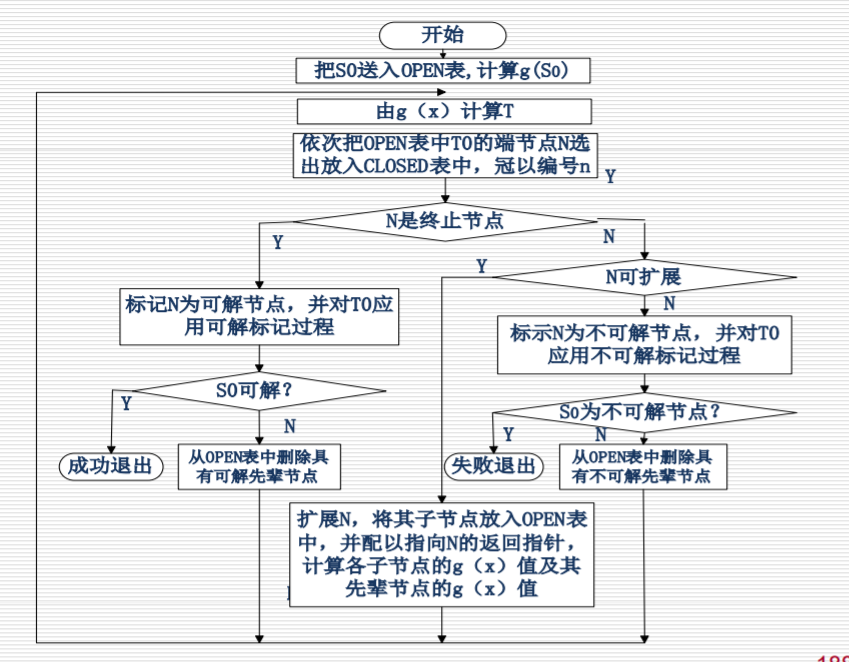
与或图搜索
广度优先搜索
- 把初始节点S0放入OPEN表。
- 把OPEN表中的第一个节点(记为节点N)取出放入CLOSED表,并冠以编号n。
- 如果节点n可扩展,则作下列工作:
- 扩展节点N,将其子节点放入OPEN表尾部,并为每个子节点配置指向父节点的指针,以备标示过程中使用。
- 考查这些节点中是否有终止节点。若有,将它们放入CLOSED表,标示这些节点为可解节点,并用可解标示过程对其先辈节点中的可解节点进行标示。 如果S0也被标示为可解节点,就得到解树,搜索成功,退出。
- 若S0不能确定为可解节点,则从OPEN表中删除具有可解先辈节点。转步2。
- 如果节点N不可扩展,则作如下工作:
- 标示节点N为不可解节点。
- 应用不可解节点标示过程对节点N的先辈节点中不可解的节点进行标示。如果初始节点S0也被标示为不可解节点,则搜索失败,退出搜索过程;
- 如果不能确定S0为不可解节点,则从OPEN表中删去具有不可解先辈的节点。转步2。

有界深度优先搜索算法
想比广度优先算法,多了一个对节点N的深度判断

启发式与或树搜索
博弈树搜索
与节点:选最小的
或节点:选最大的
4、推理
非经典推理三个改进算法的过程,包括三值逻辑
经典逻辑都是二值逻辑,即只有真(True)和假(False)两种,而非经典逻辑都是多值逻辑,如三值、四值和模糊逻辑等
多值逻辑
Kleene三值逻辑
- 三值:真T、假F、不能判定U
非单调逻辑
- 非单调就是逻辑系统中的定理随着推理的进行而并非总是递增的,就是说也可能有时要减少
- 若由某假设出发进行的推理中一旦出现不一致,即出现与假设矛盾的命题,那么允许撤消原来的假设及由它推出的全部结论
时序逻辑
- 引入时间词,如“过去”,“将来”,“有时”,“一直”等
不确定性推理=符号推演+信度计算
程度推理=符号推演+程度计算
推理结论CF的计算:CF(H)=CF(H,E)·max{0,CF(E)}
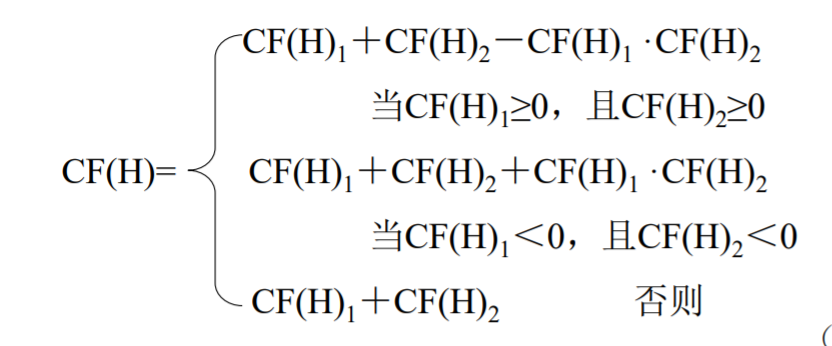
关于证据理论的例题 例8.15 (PPT 4-0 84)
贝叶斯网络
- 因果推理:因→果
- 诊断推理:果→因
- 辩解
主观贝叶斯
证据理论
基于证据理论的不确定性推理,大体可分为以下步骤:
- 建立问题的识别框架Ω;
- 给幂集2Ω定义基本概率分配函数;
- 计算所关心的子集A∈2Ω(即Ω的子集)的信任函数值Bel(A)(又称下限函数)、似真函数值Pl(A)(又称上限函数);
- 由Bel(A)、Pl(A)得出结论。
可信度方法
- 规则A→B,可信度表示为CF(B,A) (范围[-1,1])
- 还有就是一些推理计算,不展示了(PPT 4-1 114)
5、遗传算法
遗传算法的过程,原理(赌轮选择、模板定理、积木块假设),缺陷
基本思想:
- 产生初试种群
- 更具问题的目标函数构造适值函数
- 更具适值的好坏不断选择和繁殖
- 若干代后得到适应值最好的个体即为最优解

原理:
模板定理:具有低阶、短定义距以及平均适应度高于种群平均适应度的模板在子代中呈指数增长。(PPT 5-3 42)
积木块假设:遗传算法通过短定义距、低阶以及高平均适应度的模式(积木块),在遗传操作下相互结合,最终接近全局最优解。(PPT 5-3 45)
赌轮选择:各个个体被选中的概率与其适应 度函数值大小成正比。(PPT 5-3 61)
缺陷(PPT 5-2 96)
- 个体间关联性没有考虑
- 对于一些问题搜索结果往往偏离全局最优解
6、蚁群算法
蚁群算法的过程,原理,缺陷
原理:蚂蚁在寻找食物的过程中往往是随机选择路径的,但它们能感知当前地面上的信息素浓度,并倾向于往信息素浓度高的方向行进。信息素由蚂蚁自身释放,是实现蚁群内间接通信的物质。由于较短路径上蚂蚁的往返时间比较短,单位时间内经过该路径的蚂蚁多,所以信息素的积累速度比较长路径快。因此,当后续蚂蚁在路口时,就能感知先前蚂蚁留下的信息,并倾向于选择一条较短的路径前行。这种正反馈机制使得越来越多的蚂蚁在巢穴与食物之间的最短路径上行进。由于其他路径上的信息素会随着时间蒸发,最终所有的蚂蚁都在最优路径上行进。
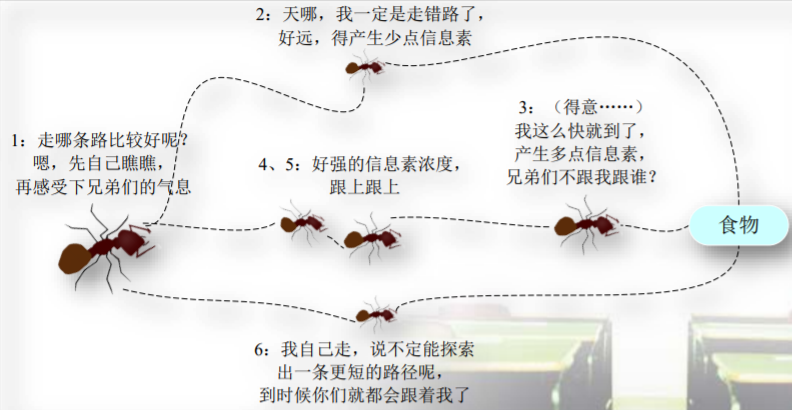
过程
-
路径构建
- 每只蚂蚁都随机选择一个城市作为其出发城市,并维护一个路径记忆向量,用来存放该蚂蚁依次经过的城市。蚂蚁在构建路径的每一步中,按照一个随机比例规则选择下一个要到达的城市。
- 长度越短、信息素浓度越大的路径被蚂蚁选择的概率越大。
-
信息素更新
-
当所有蚂蚁构建完路径后,算法将会对所有的路径进行全局信息素的更新。注意,我们所描述的是AS的ant-cycle版本,更新是在全部蚂蚁均完成了路径的构造后才进行的,信息素的浓度变化与蚂蚁在这一轮中构建的路径长度相关。
-
流程
-
在算法初始化时,问题空间中所有的边上的信息素都被初始化为τ0。
-
算法迭代每一轮,问题空间中的所有路径上的信息素都会发生蒸发,我们为所有边上的信息素乘上一个小于1的常数。信息素蒸发是自然界本身固有的特征,在算法中能够帮助避免信息素的无限积累,使得算法可以快速丢弃之前构建过的较差的路径。
-
蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素。蚂蚁构建的路径越短、释放的信息素就越多。一条边被蚂蚁爬过的次数越多、它所获得的信息素也越多。
-
迭代(2),直至算法终止。
-
-
缺陷(非PPT内容 来自https://blog.csdn.net/qq_44081582/article/details/107415925)
- 收敛速度慢
- 局部最优解问题
- 优化能力问题
- 种群多样性与收敛速度的矛盾
7、神经网络
NN 基本形态,感知器的过程
NN基本形态

当神经元i的输入信号加权和超过阈值时,输出为“1”,即“兴奋”状态;反之输出为“0”,是“抑制”状态。
NN的典型结构
- 层次型神经网络
- 前向神经网络
- 层内有互联的前向神经网络
- 有反馈的前向神经网络
- 互联型神经网络
感知器过程 PPT 5-4-1 49 + PPT 5-4-2
感知器的训练主要是反复对感知器神经网络进行仿真和学习, 最终得到最优的网络阀值和权值
- 确定我们所解决的问题的输入向量P、目标向量t,并确定各向量的维数,以及网络结构大小、神经元数目。
- 初始化:权值向量w和阀值向量b分别赋予[-1,+1]之间的随机值,并且给出训练的最大次数。
- 根据输入向量P、最新权值向量w和阀值向量b,计算网络输出向量a。
- 检查感知器输出向量与目标向量是否一致,或者是否达到了最大的训练次数,如果是则结束训练,否则转入(5)。
- 根据感知器学习规则调查权向量,并返回3)。
8、主观贝叶斯
r1: IF E1 THEN (100, 0.1) H1
r2: IF E2 THEN (50, 0.5) H2
r3: IF E3 THEN (5, 0.05) H3
( H 1 ) = 0.02 (H_1)=0.02 (H1)=0.02, P ( H 2 ) = 0.2 P(H_2)=0.2 P(H2)=0.2, P ( H 3 ) = 0.4 P(H_3)=0.4 P(H3)=0.4,计算当证据 E 1 E_1 E1, E 2 E_2 E2, E 3 E_3 E3存在或不存在时 P ( H i ∣ E i ) P(H_i | E_i) P(Hi∣Ei) 或 $P(H_i | \neg E_i) $ 的值各是多少 ( i = 1 , 2 , 3 ) (i=1, 2, 3) (i=1,2,3) ?(PPT 4-2 83)
参考书P102 例4.3
记住两个公式(分别在书P100 和 P101)
1、 P ( H ∣ E ) = L S ∗ P ( H ) ( L S − 1 ) ∗ P ( H ) + 1 P(H|E) = \frac{LS * P(H)} { (LS-1) * P(H) + 1 } P(H∣E)=(LS−1)∗P(H)+1LS∗P(H)
2、 P ( H ∣ ¬ E ) = L N ∗ P ( H ) ( L N − 1 ) ∗ P ( H ) + 1 P(H| \neg E) = \frac{LN * P(H)} { (LN-1) * P(H) + 1 } P(H∣¬E)=(LN−1)∗P(H)+1LN∗P(H)


9、单层感知器
构建一个单层感知器神经元,实现逻辑与操作。(PPT 5-4-2 8)
| x1 | x2 | d |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
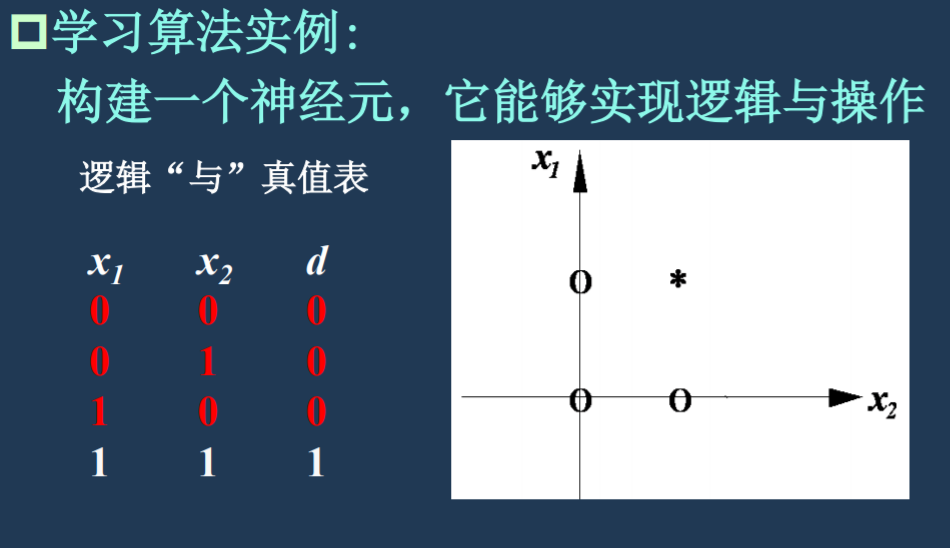

设阈值为 0.6,初始权值均为 0.1,学习率为 0.5,误差值要求为 0,神经元的激活函数为硬限幅函数,求权值 w1 与 w2。 (PPT 5-4-2 10)
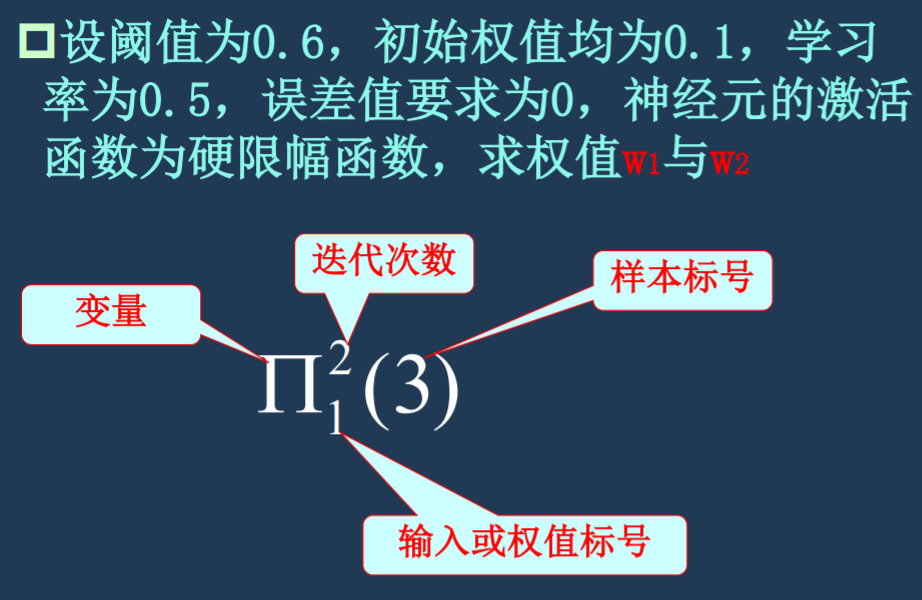




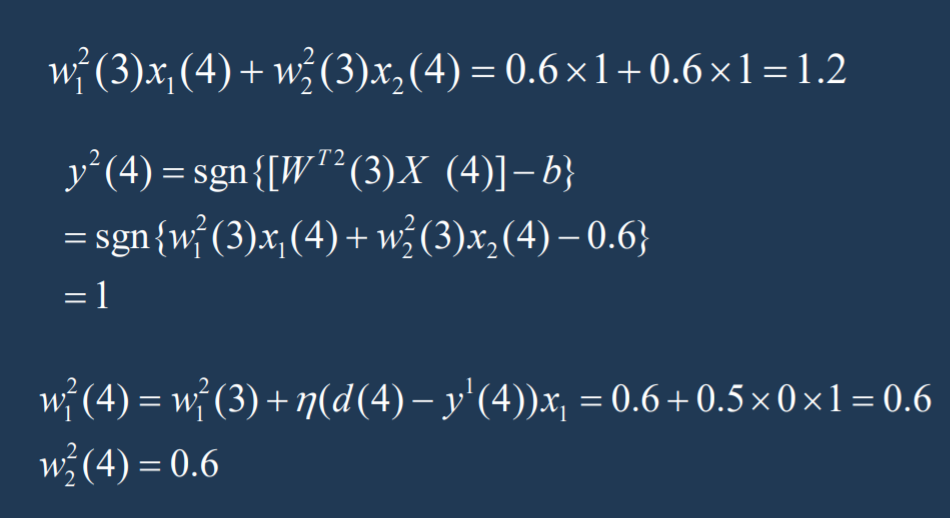

算输入:WT * X
算输出:sgn{WT*X - b}
调整权值:wi(n+1) = wi(n) + n(学习率)(d(n) - y(n))*xi
重复到输出误差为0才行
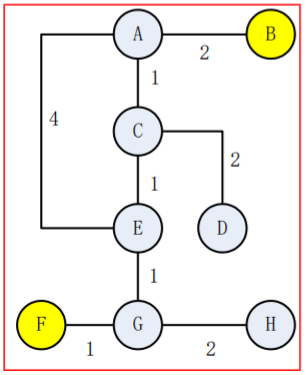
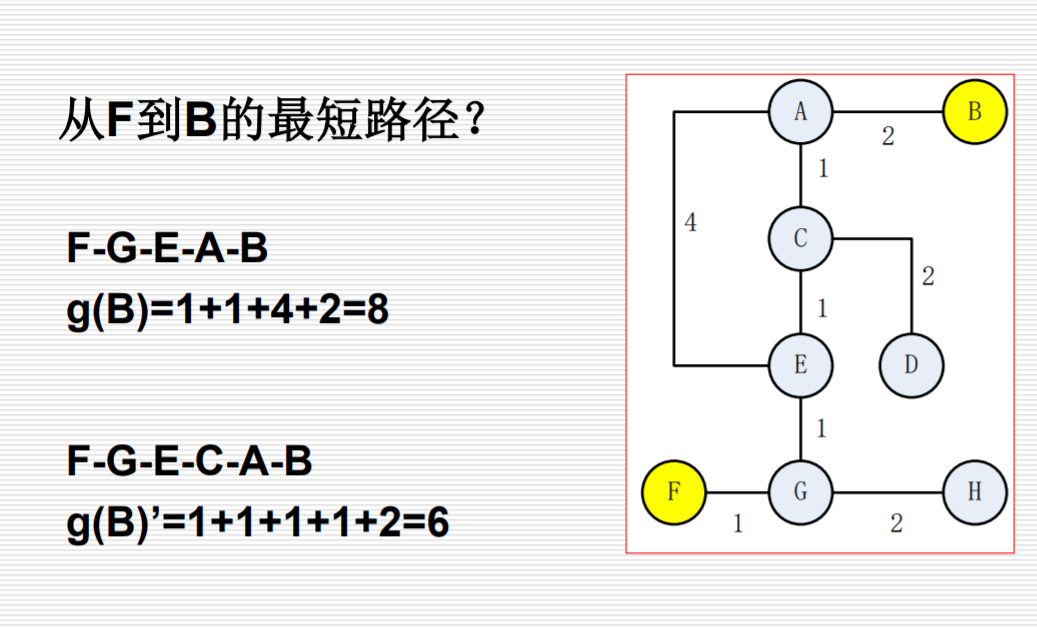
10、加权状态图搜索
加权状态图搜索,计算从 F 到 B 的最短路径,画出 open、close 表。(PPT 3-2 110)