目录
1 障碍处理与KD树2 KD树核心原理2.1 KD树的构造2.2 KD树的查找 3 仿真实现3.1 KD树基本算法3.2 ROS C++仿真
1 障碍处理与KD树
在机器人感知系统中,传感器(如激光雷达、摄像头等)会采集周围的环境数据,例如代价地图、八叉树地图等,都是环境数据的表现形式。机器人在移动过程中需要根据环境,确定当前路径上的潜在障碍物。然而,这些障碍物的数量通常非常庞大,直接遍历处理往往会产生非常高的延迟,在动态环境或高实时性任务中对下游算法非常不利。
KD树(K-Dimensional tree)是一种用于高维空间数据的高效数据结构,广泛应用于机器人障碍物感知与处理中。它的主要功能是提供快速的最近邻搜索、范围查询等操作,使机器人可以实时检测到路径上的障碍物,及时调整其运动轨迹,避免碰撞。对于复杂环境中的机器人,KD树的高效查询能力尤为重要。此外,KD树可以通过增量更新来适应这些变化,而不需要重新构建整个数据结构。这样,机器人可以持续感知并适应环境的变化,保持高效的障碍物检测和避障能力。
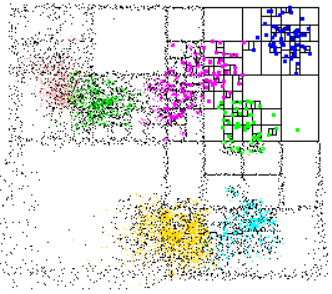
接下来通过一个案例分析KD树的原理,并展示基于ROS的实际应用效果
2 KD树核心原理
KD树是一棵空间二叉树,其中任意节点 x ∈ R k \boldsymbol{x}\in \mathbb{R} ^k x∈Rk。所有非叶子节点包含一个把空间分成两个半空间的超平面。节点的左子树组织了位于其超平面左侧的点,右子树同理。KD树不仅应用于最近邻搜索,在多维键值搜索、范围搜寻等方面也有广泛应用。
2.1 KD树的构造
KD树构造的核心是超平面的选择与划分,经典方法是随着树深度加深,轮流选择特征维度作为超平面的法向量,二分空间时只考虑样本在该维度的取值。如图所示,KD树的每个节点是二维样本,则超平面轮流以 x x x、 y y y轴为法向量,划分时小于根节点法向特征值的样本被划分到左子树,反之划分到右子树。
2.2 KD树的查找
KD树最近邻查找的核心是递归搜索。在一次迭代中,根据测试点与KD树当前节点相应特征维度的大小关系选择要搜索的子树并执行搜索。但是最近邻点不一定位于这个子树中,需要进行判断:每次查询测试点与KD树节点关系时,会更新一次最小距离 d i s t min \mathrm{dist}_{\min} distmin,最近邻点一定位于以测试点为圆心、 d i s t min \mathrm{dist}_{\min} distmin为半径的圆内;计算相应特征维距离 d i s t a x i s \mathrm{dist}_{\mathrm{axis}} distaxis,若 d i s t a x i s < d i s t min \mathrm{dist}_{\mathrm{axis}}<\mathrm{dist}_{\min} distaxis<distmin,说明当前KD树节点包含的超平面穿过了最近邻圆域,则该节点的另一子树也需要递归搜索
如图所示为KD树最近邻查找的实例。
如图(a)所示,第一次查找节点(30,40)并更新最近邻圆,由于测试点位于节点(30,40)右侧,因此需要继续查询右子树;同时最近邻圆被节点(30,40)包含的超平面 x = 30 x=30 x=30穿过,所以节点(30,40)的左侧也可能包含最近邻点,故左子树也被查询。
如图(b)所示是下一层递归时对节点(30,40)左子树根节点(5,25)的查询,由于测试点位于节点(5,25)下侧,因此需要继续查询左子树;此时最近邻圆没有更新,被节点(5,25)包含的超平面 y = 25 y=25 y=25穿过,所以节点(5,25)的上侧也可能包含最近邻点,但节点(5,25)不存在右子树,故其右子树查询退出递归。
如图(c)所示是下一层递归时对节点(5,25)左子树根节点(10,12)的查询,考虑到是叶节点,直接更新最近邻圆即可。
在节点(30,40)右子树的查询中,首先进入节点(35,45),类似地应查询其左子树,但节点(35,45)包含的超平面 y = 45 y=45 y=45没穿过最近邻圆,说明节点(35,45)右子树的所有点都在最近邻圆外部,不可能是最近邻点,可以进行剪枝,提高计算效率。
3 仿真实现
3.1 KD树基本算法
KD树的查找主要分为以下三种模式
最近邻查找
int nnSearch(const PointT& query, double* min_dist = nullptr) const{ int guess; double _min_dist = std::numeric_limits<double>::max(); _nnSearchRecursive(query, root_, &guess, &_min_dist); if (min_dist) *min_dist = _min_dist; return guess;}void _nnSearchRecursive(const PointT& query, const KDNode* node, int* guess, double* min_dist) const{ if (node == nullptr) return; const PointT& train = points_[node->idx]; const double dist = _distance(query, train); if (dist < *min_dist) { *min_dist = dist; *guess = node->idx; } const int axis = node->axis; const int dir = query[axis] < train[axis] ? 0 : 1; _nnSearchRecursive(query, node->next[dir], guess, min_dist); // if the min distance crosses the axis, the nearest neighbor maybe exist // in the other side of axis, therefore another direction should be searched const double diff = fabs(query[axis] - train[axis]); if (diff < *min_dist) _nnSearchRecursive(query, node->next[!dir], guess, min_dist);}K近邻查找
std::vector<int> knnSearch(const PointT& query, int k) const{ KnnQueue queue(k); _knnSearchRecursive(query, root_, queue, k); std::vector<int> indices(queue.size()); for (size_t i = 0; i < queue.size(); i++) indices[i] = queue[i].second; return indices;}void _knnSearchRecursive(const PointT& query, const KDNode* node, KnnQueue& queue, int k) const{ if (node == nullptr) return; const PointT& train = points_[node->idx]; const double dist = _distance(query, train); queue.push(std::make_pair(dist, node->idx)); const int axis = node->axis; const int dir = query[axis] < train[axis] ? 0 : 1; _knnSearchRecursive(query, node->next[dir], queue, k); const double diff = fabs(query[axis] - train[axis]); if ((int)queue.size() < k || diff < queue.back().first) _knnSearchRecursive(query, node->next[!dir], queue, k);}圆形近邻查找
std::vector<int> radiusSearch(const PointT& query, double radius) const{ std::vector<int> indices; _radiusSearchRecursive(query, root_, indices, radius); return indices;}void _radiusSearchRecursive(const PointT& query, const KDNode* node, std::vector<int>& indices, double radius) const{ if (node == nullptr) return; const PointT& train = points_[node->idx]; const double dist = _distance(query, train); if (dist < radius) indices.push_back(node->idx); const int axis = node->axis; const int dir = query[axis] < train[axis] ? 0 : 1; _radiusSearchRecursive(query, node->next[dir], indices, radius); const double diff = fabs(query[axis] - train[axis]); if (diff < radius) _radiusSearchRecursive(query, node->next[!dir], indices, radius);}3.2 ROS C++仿真
首先在主节点中构造KD树对象,并将代价地图的障碍信息传入KD树
rmp::common::structure::KDTree<rmp::common::geometry::Point3d> obs_kd_tree;rmp::common::geometry::Points3d obstacles;auto grid2Index = [&](int x, int y) { return x + costmap_ros_->getCostmap()->getSizeInCellsX() * y; };for (int x = 0; x < costmap_ros_->getCostmap()->getSizeInCellsX(); x++){ for (int y = 0; y < costmap_ros_->getCostmap()->getSizeInCellsY(); y++) { if (costmap_ros_->getCostmap()->getCharMap()[grid2Index(x, y)] == costmap_2d::INSCRIBED_INFLATED_OBSTACLE) { double wx, wy; costmap_ros_->getCostmap()->mapToWorld(x, y, wx, wy); obstacles.emplace_back(wx, wy); } }}obs_kd_tree.build(obstacles);rmp::common::geometry::Point3d robot_pose(start.pose.position.x, start.pose.position.y, start.pose.position.z);接着测试不同的KD树障碍物搜索算法
最近邻查找
auto idx = obs_kd_tree.nnSearch(robot_pose);Visualizer::Lines2d knn;knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>( { start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);
K近邻查找
auto obs_idx = obs_kd_tree.knnSearch(robot_pose, 10);Visualizer::Lines2d knn;for (const int idx : obs_idx){ knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>( { start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));}visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);
圆形近邻查找
auto obs_idx = obs_kd_tree.radiusSearch(robot_pose, 2.0);Visualizer::Lines2d knn;for (const int idx : obs_idx){ knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>( { start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));}visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);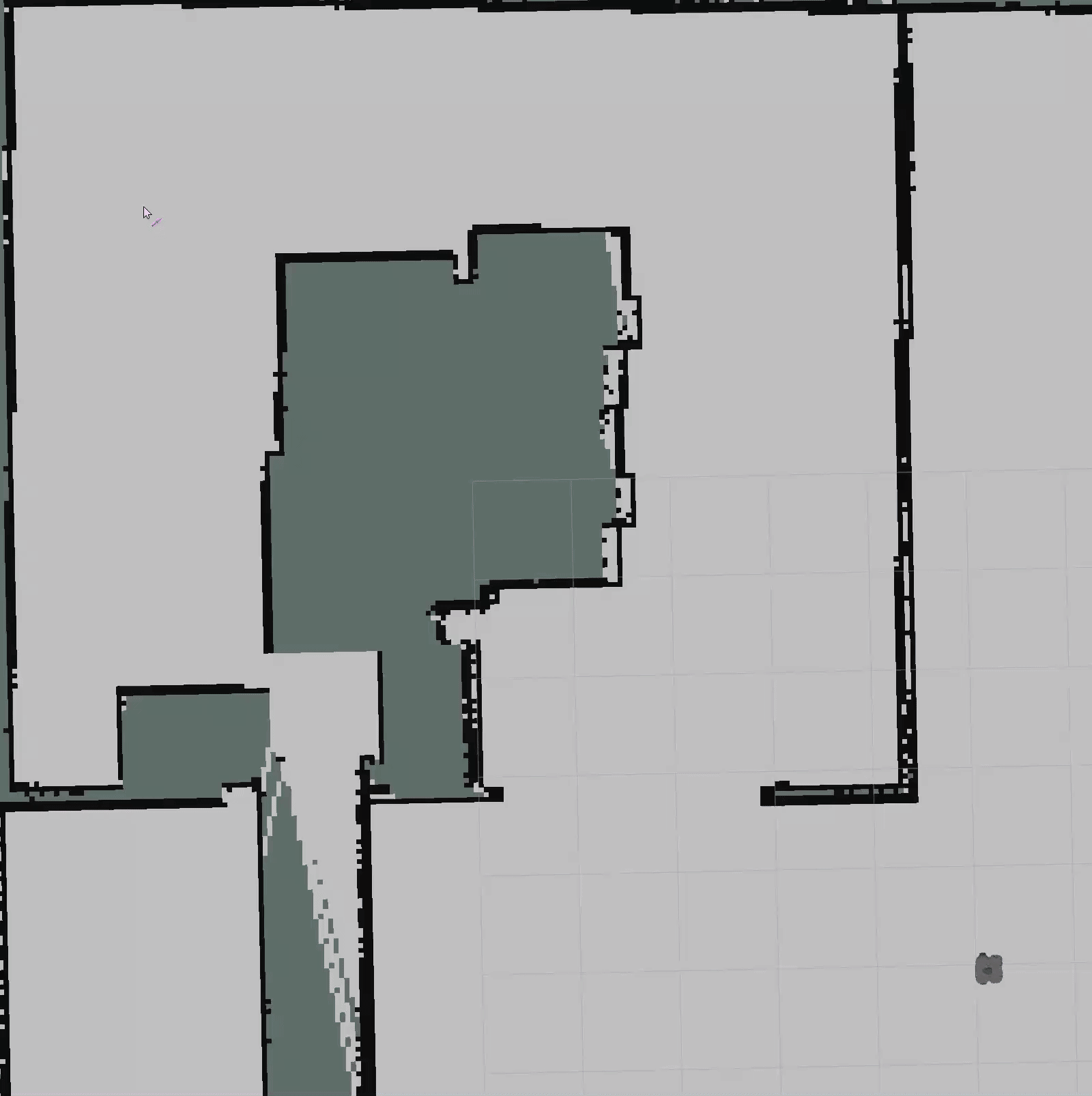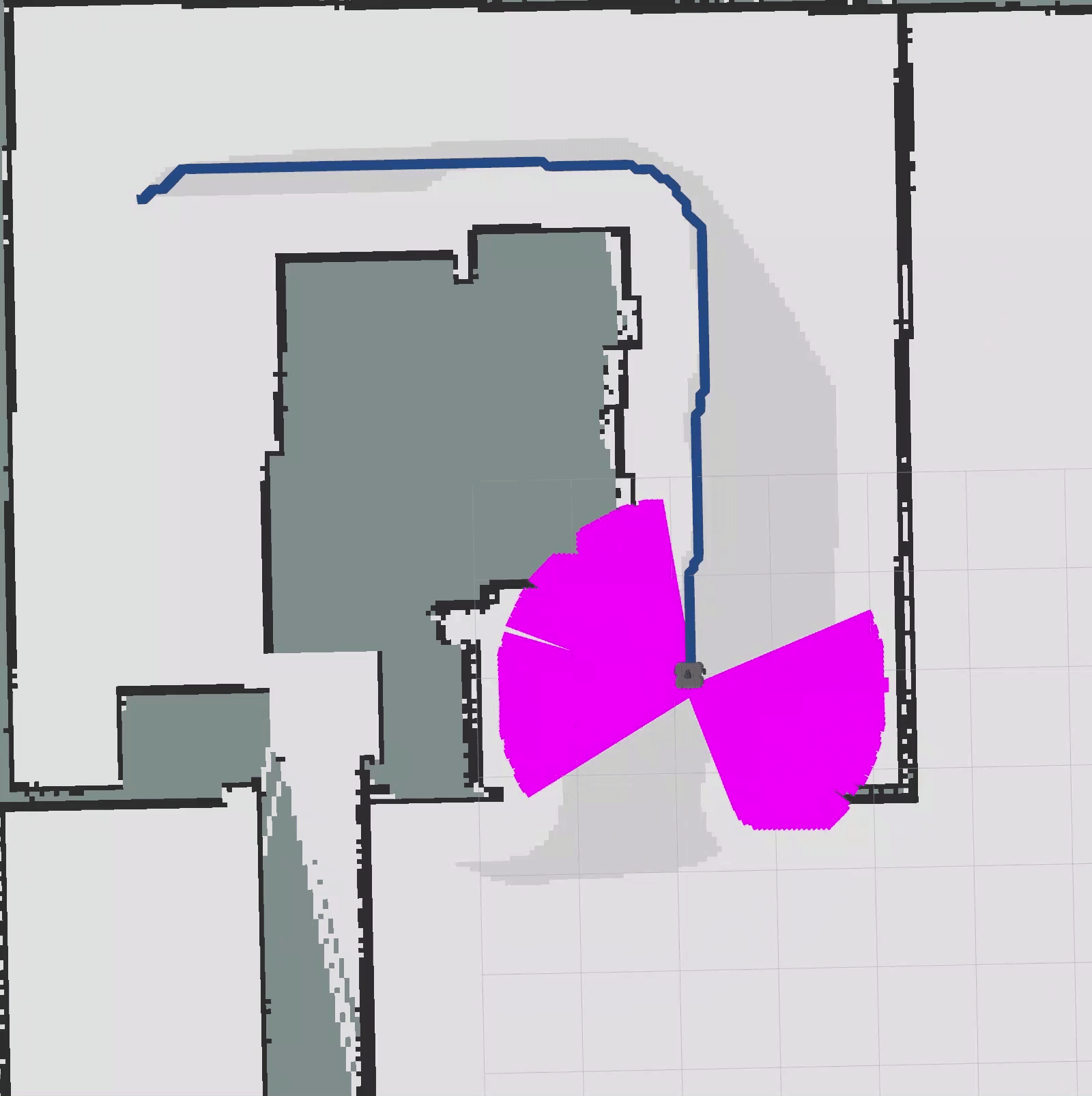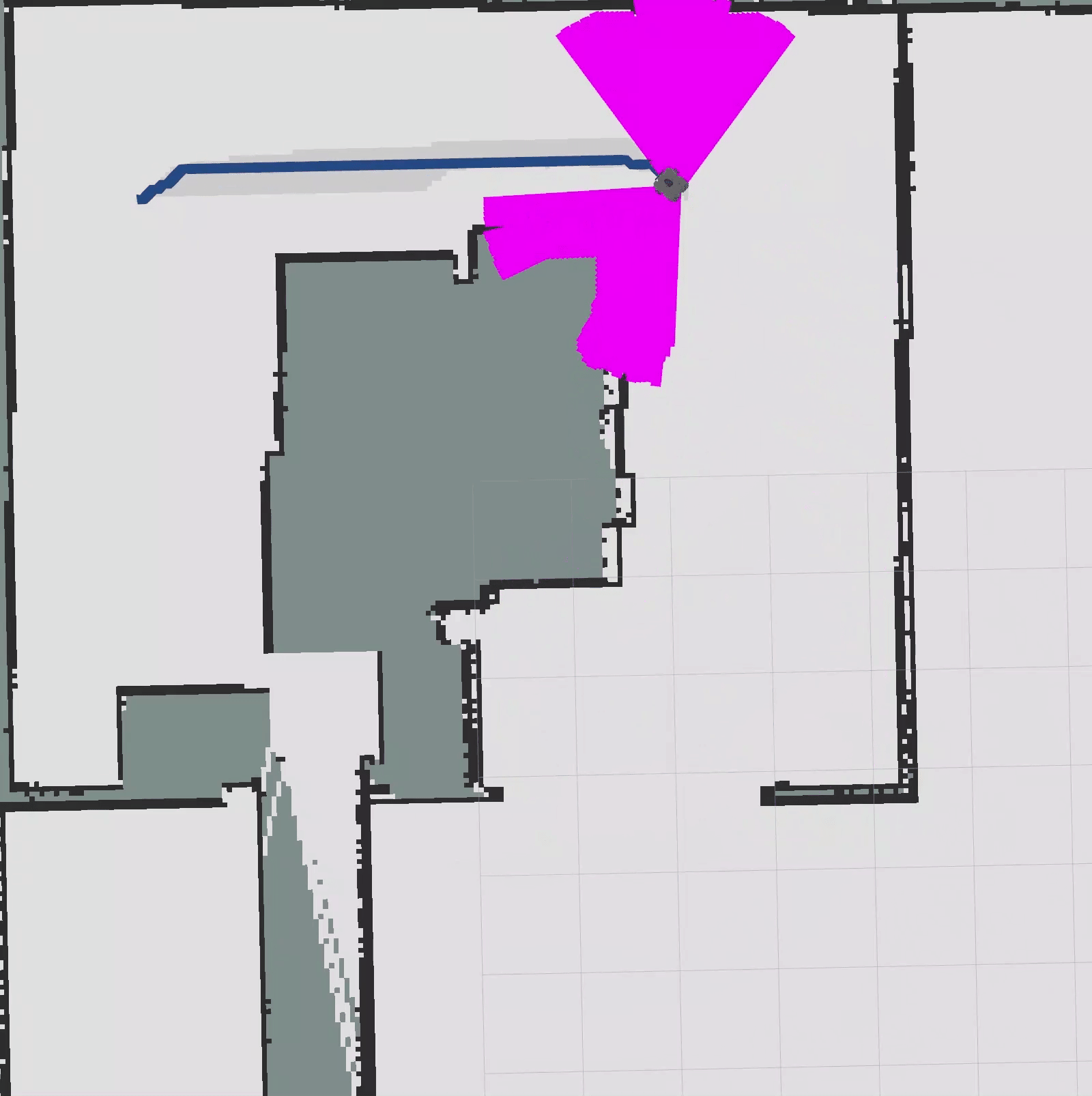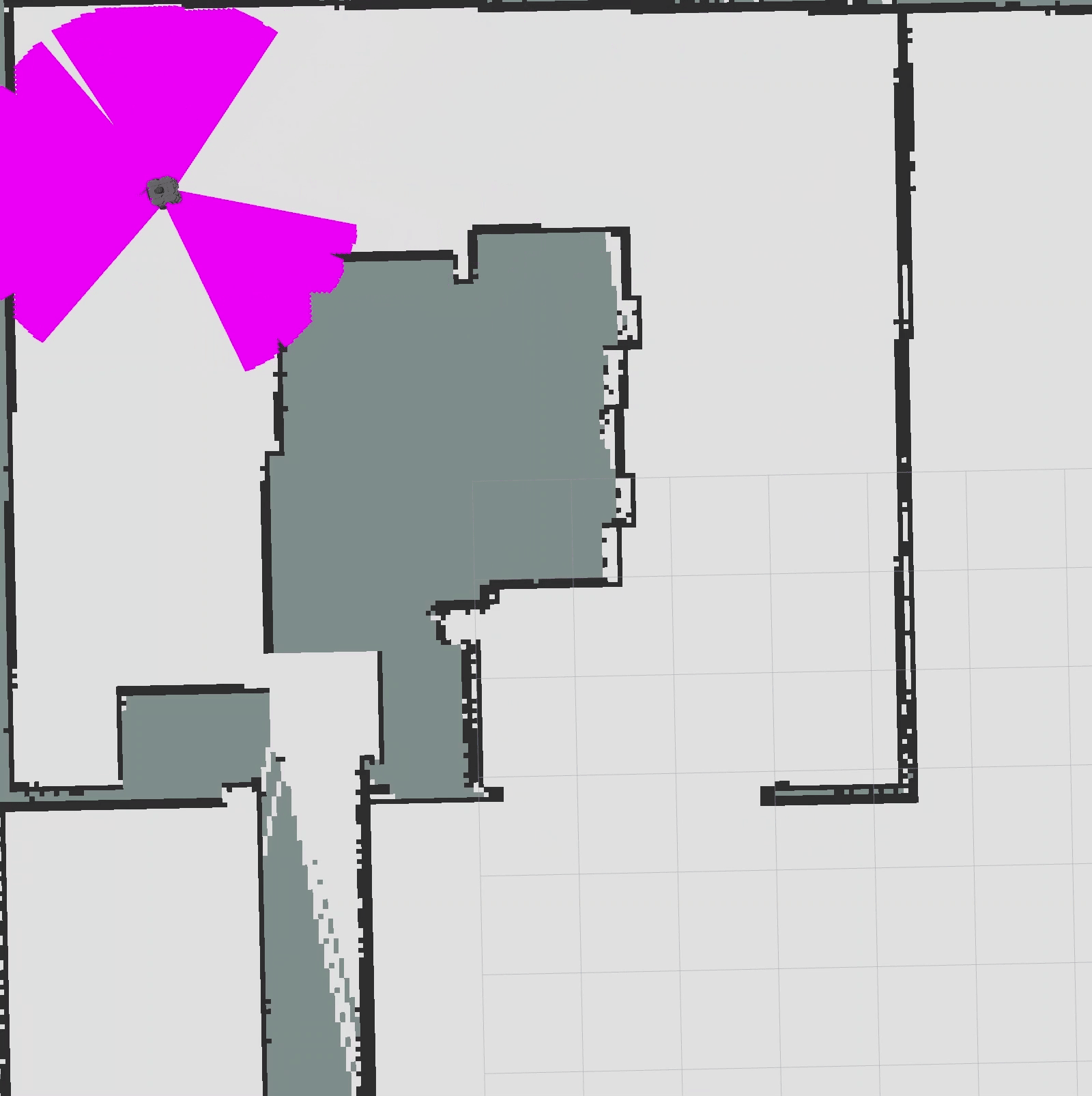
完整工程代码请联系下方博主名片获取
? 更多精彩专栏:
《ROS从入门到精通》《Pytorch深度学习实战》《机器学习强基计划》《运动规划实战精讲》…?源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系?