数独
数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵(Latin Square)。19世纪80年代,一位美国的退休建筑师格昂斯(Howard Garns)根据这种拉丁方阵发明了一种填数趣味游戏,这就是数独的雏形。20世纪70年代,人们在美国纽约的一本益智杂志《Math Puzzles and Logic Problems》上发现了这个游戏,当时被称为填数字(Number Place),这也是公认的数独最早的见报版本。——摘自百度百科
除了九宫格数独,还有许多各种变形数独(如下图),也有几个数独复合在一起的联合数独等等。
python实现数独游戏
本篇以九宫格数独为例,自定义了两个类 Matrix() 和 Sudo(),源代码见本篇末尾。
用法:Sudo(level)
参数:level = 1 ~ 7 ,分别初始化10~70个待填空格,默认值为4。
>>> sudoku = Sudo()
>>> #题目矩阵的数组
>>> sudoku.matrix
[[9, 7, 0, 6, 0, 4, 0, 0, 0],
[0, 0, 3, 5, 7, 0, 4, 6, 9],
[0, 0, 0, 2, 0, 9, 0, 7, 0],
[3, 4, 0, 8, 0, 6, 0, 1, 2],
[0, 2, 0, 0, 9, 7, 0, 5, 0],
[0, 6, 0, 0, 0, 0, 7, 0, 4],
[8, 0, 0, 0, 6, 2, 1, 3, 0],
[7, 5, 0, 9, 0, 3, 2, 4, 6],
[6, 0, 2, 0, 4, 0, 0, 0, 0]]
>>> #题目答案的元组
>>> sudoku.matrix.data
((9, 7, 5, 6, 1, 4, 3, 2, 8),
(2, 1, 3, 5, 7, 8, 4, 6, 9),
(4, 8, 6, 2, 3, 9, 5, 7, 1),
(3, 4, 7, 8, 5, 6, 9, 1, 2),
(1, 2, 8, 4, 9, 7, 6, 5, 3),
(5, 6, 9, 3, 2, 1, 7, 8, 4),
(8, 9, 4, 7, 6, 2, 1, 3, 5),
(7, 5, 1, 9, 8, 3, 2, 4, 6),
(6, 3, 2, 1, 4, 5, 8, 9, 7))
>>>
>>> #矩阵中空格坐标的元组
>>> m.zero
[(0, 2), (0, 4), (0, 6), (0, 7), (0, 8), (1, 0), (1, 1), (1, 5), (2, 0), (2, 1),
(2, 2), (2, 4), (2, 6), (2, 8), (3, 2), (3, 4), (3, 6), (4, 0), (4, 2), (4, 3),
(4, 6), (4, 8), (5, 0), (5, 2), (5, 3), (5, 4), (5, 5), (5, 7), (6, 1), (6, 2),
(6, 3), (6, 8), (7, 2), (7, 4), (8, 1), (8, 3), (8, 5), (8, 6), (8, 7), (8, 8)]
>>> 游戏操作过程
>>> m = Sudo(1)
>>> m.Question # 1~9 为已知数字, 0 表示待填的空格
6 0 3 | 8 7 5 | 0 2 1
7 2 5 | 1 3 9 | 0 6 8
1 0 8 | 2 4 0 | 5 7 3
------+-------+------
3 5 4 | 6 9 7 | 8 1 2
0 0 9 | 5 0 8 | 6 3 4
8 6 1 | 4 2 3 | 7 9 5
------+-------+------
9 8 7 | 3 5 0 | 1 4 6
4 3 6 | 9 8 1 | 2 5 7
5 1 2 | 7 0 4 | 3 8 9
>>> m.Try() #返回待填空的坐标,左上第一格坐标为(1,1),最右下一格的坐标为(9,9)
[(1, 2), (1, 7), (2, 7), (3, 2), (3, 6), (5, 1), (5, 2), (5, 5), (7, 6), (9, 5)]
>>> m.Try(1,2) #返回某一格可填的数字
{9, 4}
>>> [m.Try(x,y) for x,y in m.Try()] #返回所有空格
[{9, 4}, {9, 4}, {4}, {9}, {6}, {2}, {7}, {1}, {2}, {6}]
>>> m.Get(1,2) #获取某坐标的答案
4
>>> m.pprint() #返回任意中间状态
6 4 3 | 8 7 5 | 0 2 1
7 2 5 | 1 3 9 | 0 6 8
1 0 8 | 2 4 0 | 5 7 3
------+-------+------
3 5 4 | 6 9 7 | 8 1 2
0 0 9 | 5 0 8 | 6 3 4
8 6 1 | 4 2 3 | 7 9 5
------+-------+------
9 8 7 | 3 5 0 | 1 4 6
4 3 6 | 9 8 1 | 2 5 7
5 1 2 | 7 0 4 | 3 8 9
>>> m.Fill(1,2,4) #Fill(x,y,value) 在坐标(x,y)空格内填上数字value
>>> [m.Try(x,y) for x,y in m.Try()]
[{9}, {4}, {9}, {6}, {2}, {7}, {1}, {2}, {6}]
>>> m.Try()
[(1, 7), (2, 7), (3, 2), (3, 6), (5, 1), (5, 2), (5, 5), (7, 6), (9, 5)]
>>>
>>> m.Answer #可以提前“偷看”答案
6 4 3 | 8 7 5 | 9 2 1
7 2 5 | 1 3 9 | 4 6 8
1 9 8 | 2 4 6 | 5 7 3
------+-------+------
3 5 4 | 6 9 7 | 8 1 2
2 7 9 | 5 1 8 | 6 3 4
8 6 1 | 4 2 3 | 7 9 5
------+-------+------
9 8 7 | 3 5 2 | 1 4 6
4 3 6 | 9 8 1 | 2 5 7
5 1 2 | 7 6 4 | 3 8 9
>>>
>>>
>>> m.valid #检查所有空格是否填满并正确
False
>>> #以下代码填上全部空格,前提条件所有待填空格只有一种选择时才有效
>>> [m.Fill(x,y,z) for x,y,z in [list(x)+[*z] for x,z in list(zip(m.Try(),[m.Try(x,y) for x,y in m.Try()]))]]
>>>
>>> m.valid #检查是否已填完,全部正确返回True
True
>>> m.Question
6 0 3 | 8 7 5 | 0 2 1
7 2 5 | 1 3 9 | 0 6 8
1 0 8 | 2 4 0 | 5 7 3
------+-------+------
3 5 4 | 6 9 7 | 8 1 2
0 0 9 | 5 0 8 | 6 3 4
8 6 1 | 4 2 3 | 7 9 5
------+-------+------
9 8 7 | 3 5 0 | 1 4 6
4 3 6 | 9 8 1 | 2 5 7
5 1 2 | 7 0 4 | 3 8 9
>>> 一步完成答案
>>> sudoku = Sudo(6)
>>> sudoku.Question
0 0 0 | 0 0 0 | 0 0 0
0 0 0 | 0 0 3 | 0 7 0
8 1 0 | 4 0 9 | 0 0 2
------+-------+------
0 0 0 | 0 9 0 | 0 0 0
1 7 0 | 0 5 0 | 0 3 4
0 0 0 | 0 0 4 | 0 9 0
------+-------+------
0 0 0 | 8 0 0 | 1 4 0
0 3 0 | 0 0 0 | 0 0 0
0 0 0 | 5 0 0 | 0 0 9
>>> sudoku.valid
False
>>> sudoku.Solve()
True
>>> sudoku.valid
True
>>> sudoku.pprint()
2 4 3 | 1 7 5 | 9 6 8
9 5 6 | 2 8 3 | 4 7 1
8 1 7 | 4 6 9 | 3 5 2
------+-------+------
3 6 4 | 7 9 2 | 8 1 5
1 7 9 | 6 5 8 | 2 3 4
5 8 2 | 3 1 4 | 7 9 6
------+-------+------
7 9 5 | 8 2 6 | 1 4 3
6 3 8 | 9 4 1 | 5 2 7
4 2 1 | 5 3 7 | 6 8 9
>>> 完成时间测试
>>> sudo1 = Sudo()
>>> sudo1.timeSolve()
0.007241964340209961
>>> sudo2 = Sudo(5)
>>> sudo2.timeSolve()
0.02873539924621582
>>> sudo3 = Sudo(6)
>>> sudo3.timeSolve()
0.20312190055847168
>>> sudo4 = Sudo(7)
>>> sudo4.timeSolve()
0.022271156311035156
>>>
# 并非空格越多耗时越多;矩阵是随机产生的,个别的可能要10多秒才能出答案矩阵变换
同一数独题目,通过矩阵变换可以变化出千千万万不同的排列来。同一组数字通过变换,粗略估算一下至少有6的9次方个变化,数量为1000万以上。
转置和反序等
>>> su = Sudo()
>>> su.pprint()
5 4 0 | 7 9 0 | 0 0 3
1 3 0 | 2 0 0 | 5 6 0
0 0 8 | 3 0 0 | 0 9 1
------+-------+------
3 0 4 | 0 8 0 | 9 1 2
2 0 0 | 0 1 9 | 0 3 0
0 9 1 | 4 0 2 | 0 8 5
------+-------+------
8 7 5 | 0 0 0 | 1 0 6
0 0 3 | 1 0 4 | 0 5 0
0 1 0 | 8 0 0 | 0 0 0
>>> su.mat.T.pprint()
5 1 0 | 3 2 0 | 8 0 0
4 3 0 | 0 0 9 | 7 0 1
0 0 8 | 4 0 1 | 5 3 0
------+-------+------
7 2 3 | 0 0 4 | 0 1 8
9 0 0 | 8 1 0 | 0 0 0
0 0 0 | 0 9 2 | 0 4 0
------+-------+------
0 5 0 | 9 0 0 | 1 0 0
0 6 9 | 1 3 8 | 0 5 0
3 0 1 | 2 0 5 | 6 0 0
>>> su.mat.T1.pprint()
3 0 0 | 0 9 7 | 0 4 5
0 6 5 | 0 0 2 | 0 3 1
1 9 0 | 0 0 3 | 8 0 0
------+-------+------
2 1 9 | 0 8 0 | 4 0 3
0 3 0 | 9 1 0 | 0 0 2
5 8 0 | 2 0 4 | 1 9 0
------+-------+------
6 0 1 | 0 0 0 | 5 7 8
0 5 0 | 4 0 1 | 3 0 0
0 0 0 | 0 0 8 | 0 1 0
>>> su.mat.T2.pprint()
0 1 0 | 8 0 0 | 0 0 0
0 0 3 | 1 0 4 | 0 5 0
8 7 5 | 0 0 0 | 1 0 6
------+-------+------
0 9 1 | 4 0 2 | 0 8 5
2 0 0 | 0 1 9 | 0 3 0
3 0 4 | 0 8 0 | 9 1 2
------+-------+------
0 0 8 | 3 0 0 | 0 9 1
1 3 0 | 2 0 0 | 5 6 0
5 4 0 | 7 9 0 | 0 0 3
>>> su.mat.T3.pprint()
0 0 0 | 0 0 8 | 0 1 0
0 5 0 | 4 0 1 | 3 0 0
6 0 1 | 0 0 0 | 5 7 8
------+-------+------
5 8 0 | 2 0 4 | 1 9 0
0 3 0 | 9 1 0 | 0 0 2
2 1 9 | 0 8 0 | 4 0 3
------+-------+------
1 9 0 | 0 0 3 | 8 0 0
0 6 5 | 0 0 2 | 0 3 1
3 0 0 | 0 9 7 | 0 4 5
>>> 交换大行或大列
>>> su = Sudo()
>>> su.pprint()
0 0 0 | 0 7 2 | 5 3 8
5 8 0 | 0 3 0 | 0 0 0
0 3 7 | 0 8 0 | 0 0 1
------+-------+------
3 0 0 | 6 9 8 | 0 0 0
8 2 0 | 7 0 4 | 0 5 0
0 0 1 | 0 0 0 | 9 0 4
------+-------+------
9 6 0 | 8 4 0 | 0 2 5
0 5 8 | 0 2 1 | 0 0 6
0 1 4 | 3 0 5 | 8 0 7
>>> su.mat.R(1,2).pprint()
3 0 0 | 6 9 8 | 0 0 0
8 2 0 | 7 0 4 | 0 5 0
0 0 1 | 0 0 0 | 9 0 4
------+-------+------
0 0 0 | 0 7 2 | 5 3 8
5 8 0 | 0 3 0 | 0 0 0
0 3 7 | 0 8 0 | 0 0 1
------+-------+------
9 6 0 | 8 4 0 | 0 2 5
0 5 8 | 0 2 1 | 0 0 6
0 1 4 | 3 0 5 | 8 0 7
>>> su.mat.R(1,3).pprint()
9 6 0 | 8 4 0 | 0 2 5
0 5 8 | 0 2 1 | 0 0 6
0 1 4 | 3 0 5 | 8 0 7
------+-------+------
0 0 0 | 0 7 2 | 5 3 8
5 8 0 | 0 3 0 | 0 0 0
0 3 7 | 0 8 0 | 0 0 1
------+-------+------
3 0 0 | 6 9 8 | 0 0 0
8 2 0 | 7 0 4 | 0 5 0
0 0 1 | 0 0 0 | 9 0 4
>>> su.mat.R(2,3).pprint()
9 6 0 | 8 4 0 | 0 2 5
0 5 8 | 0 2 1 | 0 0 6
0 1 4 | 3 0 5 | 8 0 7
------+-------+------
3 0 0 | 6 9 8 | 0 0 0
8 2 0 | 7 0 4 | 0 5 0
0 0 1 | 0 0 0 | 9 0 4
------+-------+------
0 0 0 | 0 7 2 | 5 3 8
5 8 0 | 0 3 0 | 0 0 0
0 3 7 | 0 8 0 | 0 0 1
>>> su.mat.C(1,2).pprint()
8 4 0 | 9 6 0 | 0 2 5
0 2 1 | 0 5 8 | 0 0 6
3 0 5 | 0 1 4 | 8 0 7
------+-------+------
6 9 8 | 3 0 0 | 0 0 0
7 0 4 | 8 2 0 | 0 5 0
0 0 0 | 0 0 1 | 9 0 4
------+-------+------
0 7 2 | 0 0 0 | 5 3 8
0 3 0 | 5 8 0 | 0 0 0
0 8 0 | 0 3 7 | 0 0 1
>>> 交换小行或小列
>>> su = Sudo()
>>> su.pprint()
2 4 0 | 5 0 0 | 9 6 3
3 0 0 | 0 0 6 | 4 0 7
0 7 6 | 0 4 9 | 0 0 0
------+-------+------
4 0 5 | 6 0 0 | 0 0 2
1 8 0 | 7 5 2 | 0 3 0
0 2 0 | 0 0 0 | 0 9 5
------+-------+------
0 5 4 | 8 0 3 | 1 2 0
0 0 0 | 9 0 0 | 0 0 8
8 0 3 | 2 6 4 | 0 0 9
>>> su.mat.Rn(2,1,3).pprint()
2 4 0 | 5 0 0 | 9 6 3
3 0 0 | 0 0 6 | 4 0 7
0 7 6 | 0 4 9 | 0 0 0
------+-------+------
0 2 0 | 0 0 0 | 0 9 5
1 8 0 | 7 5 2 | 0 3 0
4 0 5 | 6 0 0 | 0 0 2
------+-------+------
0 5 4 | 8 0 3 | 1 2 0
0 0 0 | 9 0 0 | 0 0 8
8 0 3 | 2 6 4 | 0 0 9
>>> su.mat.Cn(1,2,3).pprint()
2 0 4 | 5 0 0 | 9 6 3
3 0 0 | 0 0 6 | 4 0 7
0 6 7 | 0 4 9 | 0 0 0
------+-------+------
4 5 0 | 6 0 0 | 0 0 2
1 0 8 | 7 5 2 | 0 3 0
0 0 2 | 0 0 0 | 0 9 5
------+-------+------
0 4 5 | 8 0 3 | 1 2 0
0 0 0 | 9 0 0 | 0 0 8
8 3 0 | 2 6 4 | 0 0 9
>>> 自定义数独题目
以矩阵样本matrixSample为列:
>>> matrixSample
[[8, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 6, 0, 0, 0, 0, 0],
[0, 7, 0, 0, 9, 0, 2, 0, 0],
[0, 5, 0, 0, 0, 7, 0, 0, 0],
[0, 0, 0, 0, 4, 5, 7, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 3, 0],
[0, 0, 1, 0, 0, 0, 0, 6, 8],
[0, 0, 8, 5, 0, 0, 0, 1, 0],
[0, 9, 0, 0, 0, 0, 4, 0, 0]]
>>> m = Sudo(0)
>>> m.Create(matrixSample)
Solving...
Soluted!
>>> m.Question
8 0 0 | 0 0 0 | 0 0 0
0 0 3 | 6 0 0 | 0 0 0
0 7 0 | 0 9 0 | 2 0 0
------+-------+------
0 5 0 | 0 0 7 | 0 0 0
0 0 0 | 0 4 5 | 7 0 0
0 0 0 | 1 0 0 | 0 3 0
------+-------+------
0 0 1 | 0 0 0 | 0 6 8
0 0 8 | 5 0 0 | 0 1 0
0 9 0 | 0 0 0 | 4 0 0
>>> m.Answer
8 1 2 | 7 5 3 | 6 4 9
9 4 3 | 6 8 2 | 1 7 5
6 7 5 | 4 9 1 | 2 8 3
------+-------+------
1 5 4 | 2 3 7 | 8 9 6
3 6 9 | 8 4 5 | 7 2 1
2 8 7 | 1 6 9 | 5 3 4
------+-------+------
5 2 1 | 9 7 4 | 3 6 8
4 3 8 | 5 2 6 | 9 1 7
7 9 6 | 3 1 8 | 4 5 2
>>> 批量生成数独题目
Sudo.build(n, level)
n = 1~50 ; level = 1~7
矩阵数据保存在全局变量 Sudoku
>>> Sudo.build(6,5)
No. 1:
8 0 0 | 0 7 0 | 0 0 0
0 0 0 | 1 0 0 | 0 0 0
0 3 0 | 0 0 9 | 0 0 2
------+-------+------
3 0 0 | 0 0 6 | 0 0 1
0 1 9 | 0 0 0 | 6 0 4
0 0 6 | 3 0 0 | 7 0 5
------+-------+------
5 7 8 | 9 3 0 | 0 0 0
9 6 3 | 8 0 4 | 0 0 7
0 0 0 | 5 0 7 | 0 0 9
No. 2:
0 2 3 | 0 5 0 | 1 6 0
0 0 0 | 0 0 0 | 0 7 9
0 1 8 | 0 0 7 | 0 0 0
------+-------+------
0 0 0 | 0 0 9 | 0 0 0
0 0 0 | 0 7 0 | 5 0 3
0 0 0 | 5 0 1 | 0 0 4
------+-------+------
8 0 6 | 7 4 3 | 0 0 0
4 0 1 | 0 0 5 | 0 3 0
0 3 2 | 0 0 6 | 0 4 7
No. 3:
5 2 9 | 0 6 0 | 0 7 3
0 4 8 | 2 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 8 0
------+-------+------
4 0 0 | 0 0 0 | 0 0 1
0 0 0 | 0 9 0 | 0 3 4
2 9 7 | 0 4 0 | 0 0 0
------+-------+------
0 5 0 | 0 0 0 | 2 1 0
0 6 0 | 0 1 0 | 0 4 7
0 0 0 | 3 2 6 | 5 9 0
No. 4:
2 0 4 | 0 0 0 | 1 0 0
0 3 0 | 0 0 0 | 0 0 0
6 8 0 | 3 4 0 | 0 7 0
------+-------+------
3 4 0 | 0 8 0 | 0 0 0
0 0 0 | 2 0 4 | 6 0 3
0 0 2 | 6 3 0 | 0 0 4
------+-------+------
4 6 0 | 8 7 0 | 2 1 0
8 0 0 | 9 0 2 | 0 0 6
0 0 3 | 0 0 0 | 0 0 0
No. 5:
8 5 0 | 6 0 3 | 0 0 0
0 0 6 | 0 0 9 | 0 5 8
9 0 0 | 0 5 8 | 6 0 0
------+-------+------
0 4 0 | 0 0 0 | 9 0 0
0 0 0 | 0 0 4 | 5 6 3
0 0 9 | 5 3 0 | 7 0 0
------+-------+------
6 3 8 | 0 4 0 | 0 0 0
0 0 0 | 0 1 0 | 0 3 0
0 0 0 | 0 6 0 | 8 9 0
No. 6:
9 4 1 | 0 0 8 | 3 5 7
0 0 7 | 0 0 0 | 0 6 9
0 0 0 | 0 0 0 | 0 0 1
------+-------+------
0 0 5 | 0 0 0 | 0 1 2
0 0 6 | 0 8 0 | 5 0 0
7 0 8 | 0 0 0 | 6 0 4
------+-------+------
6 7 0 | 8 0 0 | 0 0 0
2 0 4 | 0 0 0 | 0 0 6
0 0 0 | 7 0 6 | 9 0 8
>>>
>>> Sudoku[0]
[[8, 0, 0, 0, 7, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 3, 0, 0, 0, 9, 0, 0, 2], [3, 0, 0, 0, 0, 6, 0, 0, 1],
[0, 1, 9, 0, 0, 0, 6, 0, 4], [0, 0, 6, 3, 0, 0, 7, 0, 5],
[5, 7, 8, 9, 3, 0, 0, 0, 0], [9, 6, 3, 8, 0, 4, 0, 0, 7],
[0, 0, 0, 5, 0, 7, 0, 0, 9]]
>>> Sudoku[5]
[[9, 4, 1, 0, 0, 8, 3, 5, 7], [0, 0, 7, 0, 0, 0, 0, 6, 9],
[0, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 5, 0, 0, 0, 0, 1, 2],
[0, 0, 6, 0, 8, 0, 5, 0, 0], [7, 0, 8, 0, 0, 0, 6, 0, 4],
[6, 7, 0, 8, 0, 0, 0, 0, 0], [2, 0, 4, 0, 0, 0, 0, 0, 6],
[0, 0, 0, 7, 0, 6, 9, 0, 8]]
>>>
>>> Sudoku[2].pprint()
5 2 9 | 0 6 0 | 0 7 3
0 4 8 | 2 0 0 | 0 0 0
0 0 0 | 0 0 0 | 0 8 0
------+-------+------
4 0 0 | 0 0 0 | 0 0 1
0 0 0 | 0 9 0 | 0 3 4
2 9 7 | 0 4 0 | 0 0 0
------+-------+------
0 5 0 | 0 0 0 | 2 1 0
0 6 0 | 0 1 0 | 0 4 7
0 0 0 | 3 2 6 | 5 9 0
>>> 实战“世界最难数独”
出自搜狗百科词条“世界最难数独”,感觉这个“最”有点水份;难度不是太大,程序用时2.91秒。
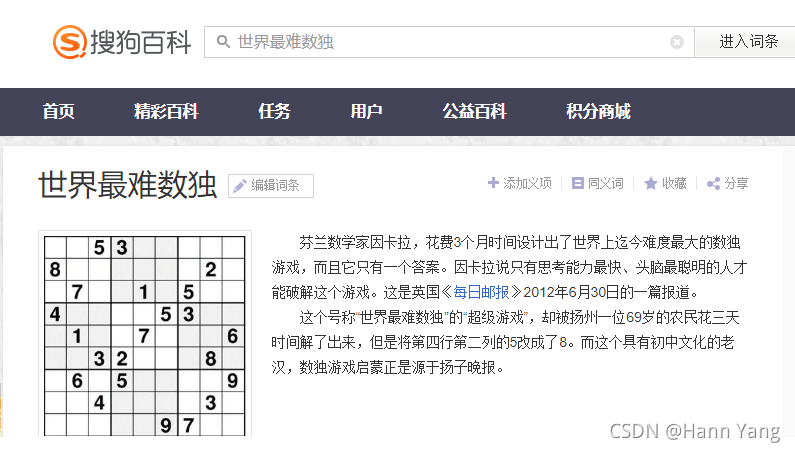
>>> m = Sudo()
>>> m.Create([
[0,0,5,3,0,0,0,0,0],
[8,0,0,0,0,0,0,2,0],
[0,7,0,0,1,0,5,0,0],
[4,0,0,0,0,5,3,0,0],
[0,1,0,0,7,0,0,0,6],
[0,0,3,2,0,0,0,8,0],
[0,6,0,5,0,0,0,0,9],
[0,0,4,0,0,0,0,3,0],
[0,0,0,0,0,9,7,0,0]])
Solving...
Soluted!
>>> m.Question
0 0 5 | 3 0 0 | 0 0 0
8 0 0 | 0 0 0 | 0 2 0
0 7 0 | 0 1 0 | 5 0 0
------+-------+------
4 0 0 | 0 0 5 | 3 0 0
0 1 0 | 0 7 0 | 0 0 6
0 0 3 | 2 0 0 | 0 8 0
------+-------+------
0 6 0 | 5 0 0 | 0 0 9
0 0 4 | 0 0 0 | 0 3 0
0 0 0 | 0 0 9 | 7 0 0
>>> m.Answer
1 4 5 | 3 2 7 | 6 9 8
8 3 9 | 6 5 4 | 1 2 7
6 7 2 | 9 1 8 | 5 4 3
------+-------+------
4 9 6 | 1 8 5 | 3 7 2
2 1 8 | 4 7 3 | 9 5 6
7 5 3 | 2 9 6 | 4 8 1
------+-------+------
3 6 7 | 5 4 2 | 8 1 9
9 8 4 | 7 6 1 | 2 3 5
5 2 1 | 8 3 9 | 7 6 4
>>> m.timeSolve()
2.914081335067749
>>> 完整代码
class Matrix():
def __init__(self):
self.val = [[0 for _ in range(9)] for _ in range(9)]
self.data = tuple(tuple(j for j in i) for i in self.val)
def __repr__(self):
return str(self.val)
def __eq__(self,other):
return all([self[i]==s for i,s in enumerate(other.val)])
def __getitem__(self,item):
return self.val[item]
def __setitem__(self,item,x):
if len(x)==9 or set(x)=={i for i in range(1,10)}:
self.val[item] = list(x)
else:
raise ValueError('x is list(), and its length is 9')
def init1(self,lst=None):
from random import sample
from random import choice
if lst!=None and isinstance(lst,list):
if set(lst)!={i for i in range(1,10)}: lst=None
while not self.valid:
for i in range(9): self[i]=[0 for _ in range(9)]
self.val[0] = lst if lst!=None else sample([_ for _ in range(1,10)],9)
for i in range(2):
if i==0:
self[1][:3] = sample(set(self[0])-set(self[0][:3]),3)
self[2][:3] = sample(set(self[0])-set(self.N[0]),3)
else:
self[0][3:] = sample(set(self.T[0])-set(self[0]),6)
self[1][3:-3] = sample(set(self[0])-set(self[0][3:-3])-set(self[1]),3)
self[2][3:-3] = sample(set(self[0])-set(self.N[1]),3)
self[1][-3:] = sample(set(self[0])-set(self[1]),3)
self[2][-3:] = sample(set(self[0])-set(self[2]),3)
self.val = self.T.val
for i in range(3,9):
for j in range(3,9):
t = self.fill(i,j)
if t!=set(): self[i][j]=choice(list(t))
else:break
if t==set():break
self.data = tuple(tuple(j for j in i) for i in self.val)
return self
def init(self,lst=None):
from random import sample
if lst!=None and isinstance(lst,list):
if set(lst)!={i for i in range(1,10)}: lst=None
t = False
while not t:
for i in range(9): self[i]=[0 for _ in range(9)]
self.val[0] = lst if lst!=None else sample([_ for _ in range(1,10)],9)
self[1][:3] = sample(set(self[0])-set(self[0][:3]),3)
self[2][:3] = sample(set(self[0])-set(self.N[0]),3)
#self[1][3:-3] = sample(set(self[0])-set(self[0][3:-3])-set(self[1]),3)
#self[2][3:-3] = sample(set(self[0])-set(self.N[1]),3)
t = Matrix.solve(self.val)
self.data = tuple(tuple(j for j in i) for i in self.val)
return self
@property
def valid(self):
return all([set(i)=={i for i in range(1,10)} for i in self.val+self.N.val+self.T.val])
def fill(self,i,j):
if self[i][j]:return self[i][j]
t = [x for x in [y for y in range(1,10) if y not in self[i]] if x not in self.T[j]]
return {x for x in t if x not in self.N[i//3*3+j//3]}
@property
def T(self):
t = Matrix()
t.val = [[self.val[i][j] for i in range(9)] for j in range(9)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
@property
def T1(self):
t = Matrix()
t.val = [[self[i][j] for j in range(8,-1,-1)] for i in range(9)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
@property
def T2(self):
t = Matrix()
t.val = [[self[i][j] for j in range(9)] for i in range(8,-1,-1)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
@property
def T3(self):
t = Matrix()
t.val = [[self[i][j] for j in range(8,-1,-1)] for i in range(8,-1,-1)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
@property
def N(self):
t = Matrix()
t.val = [[self[i+3*m][j+3*n] for i in range(3) for j in range(3)]
for m in range(3) for n in range(3)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
@property
def M(self):
t = Matrix()
t.val[3],t.val[5] = t.val[5],t.val[3]
t.val = [[self[i+3*m][j+3*n] for i in range(3) for j in range(3)]
for m in range(3) for n in range(3)]
t.data = tuple(tuple(j for j in i) for i in t.val)
return t
def R(self,x,y):
if x not in [1,2,3] or y not in [1,2,3]:
raise ValueError('x or y range: 1,2,3')
if x==y: return self
s = Matrix()
s.val = self.val
if x>y: x,y=y,x
if x==1 and y==2:
s[0],s[1],s[2],s[3],s[4],s[5] = s[3],s[4],s[5],s[0],s[1],s[2]
if x==1 and y==3:
s[0],s[1],s[2],s[6],s[7],s[8] = s[6],s[7],s[8],s[0],s[1],s[2]
if x==2 and y==3:
s[3],s[4],s[5],s[6],s[7],s[8] = s[6],s[7],s[8],s[3],s[4],s[5]
return s
def Rn(self,n,x,y):
if n not in [1,2,3] or x not in [1,2,3] or y not in [1,2,3]:
raise ValueError('n or x or y range: 1,2,3')
if x==y: return self
if x>y: x,y=y,x
x,y = x-1+(n-1)*3,y-1+(n-1)*3
s = self.T.T
s[x],s[y] = s[y],s[x]
return s
def Cn(self,n,x,y):
if n not in [1,2,3] or x not in [1,2,3] or y not in [1,2,3]:
raise ValueError('n or x or y range: 1,2,3')
if x==y: return self
if x>y: x,y=y,x
x,y = x-1+(n-1)*3,y-1+(n-1)*3
s = self.T
s[x],s[y] = s[y],s[x]
return s.T
def C(self,x,y):
if x not in [1,2,3] or y not in [1,2,3]:
raise ValueError('x or y range: 1,2,3')
if x==y: return self
s = self.T
s.R(x,y)
return s.T
def pprint(self):
for k,i in enumerate(self.val):
for j,n in enumerate(i):
print(n,end='' if j==8 else ' | ' if j%3==2 else ' ')
print()
if k%3==2 and k!=8: print('-'*6+'+'+'-'*7+'+'+'-'*6)
def __find__(mat,i,j):
for x in range(i,9):
for y in range(j,9):
if mat[x][y]==0: return x,y
for x in range(9):
for y in range(9):
if mat[x][y]==0: return x,y
return -1,-1
def __valid__(mat,i,j,n):
if all([n!=mat[i][j] for j in range(9)]):
if all([n!=mat[i][j] for i in range(9)]):
X,Y = i//3*3,j//3*3
for x in range(X,X+3):
for y in range(Y,Y+3):
if mat[x][y]==n: return False
return True
return False
def solve(mat,i=0,j=0):
i,j = Matrix.__find__(mat,i,j)
if i == -1: return True
for n in range(1,10):
if Matrix.__valid__(mat,i,j,n):
mat[i][j] = n
if Matrix.solve(mat,i,j): return True
mat[i][j] = 0
return False
def create(self,mat):
if mat==None and isinstance(mat,list):
raise ValueError('mat is a list of 9x9 Matrix')
if not all([len(j)==9 for j in mat]) or len(mat)!=9:
print('Sudoku must be a 9x9 Matrix')
return
self.val = mat
t = self.T.T
tmp = [i for i in t.val+t.N.val+t.T.val]
for i in tmp:
j = [j for j in i if j!=0]
if len(j)!=len(set(j)):
print('Duplicate values in a row(or column or block).')
return
print('Solving...')
if t.solve():
ret = Sudo()
print('Soluted!')
ret.mat.val = mat
self.data=ret.mat.data = tuple(tuple(j for j in i) for i in t.val)
return ret
else:
self.data = ['Nil']
print('No solution.')
@property
def answer(self):
sudo = Matrix()
sudo.val = self.data
sudo.pprint()
class Sudo():
def __init__(self,level=4):
t = Matrix()
self.mat = self.matrix = t.init()
if level not in range(8):
raise ValueError('level range: 1,2,3,4,5,6,7')
zero = []
from random import choice
while len(zero)<level*10:
if level==0: break
t = [i for i in range(9)]
t = (choice(t),choice(t))
if t not in zero: zero.append(t)
for i in zero:
self.Modify(i[0]+1,i[1]+1,0)
self.zero = sorted(zero)
def __repr__(self):
return str(self.mat)
def pprint(self):
self.matrix.pprint()
@property
def valid(self):
return self.matrix.valid
def build(n,level=4):
global Sudoku
if not isinstance(n,int) or n<1 or n>50:
raise ValueError('level range: 1,2,3,...,50')
#print('Initializing...')
Sudoku = []
for i in range(n):
Sudoku.append(Sudo(level))
for i,m in enumerate(Sudoku):
print(f'No. {i+1}:')
m.pprint()
def Get(self,x,y):
if x*y==0 or not -10<x<10 or not -10<y<10:
raise ValueError('0<|x|,|y|<10')
if x>0: x-=1
if y>0: y-=1
return self.mat.data[x][y]
def Try(self,x=0,y=0):
if x==0==y:
return [(i+1,j+1) for i in range(9) for j in range(9) if self.mat[i][j]==0]
if x*y==0 or not -10<x<10 or not -10<y<10:
raise ValueError('0<|x|,|y|<10')
if x>0: x-=1
if y>0: y-=1
num = self.mat.val[x][y]
if num: return num
return self.mat.fill(x,y)
def Fill(self,x,y,value):
if x*y==0 or not -10<x<10 or not -10<y<10:
raise ValueError('0<|x|,|y|<10')
if x>0: x-=1
if y>0: y-=1
if self.mat.val[x][y]==0:
self.mat.val[x][y] = value
return True
else:
return False
def Modify(self,x,y,value):
if x*y==0 or not -10<x<10 or not -10<y<10:
print(x,y)
raise ValueError('0<|x|,|y|<10')
if x>0: x-=1
if y>0: y-=1
if self.mat.data[x][y]!=0:
self.mat.val[x][y] = value
return True
else:
return False
@property
def Question(self):
sudo = self
sudo.val = self.mat.data
for i in self.zero:
sudo.Fill(i[0]+1,i[1]+1,0)
sudo.pprint()
@property
def Answer(self):
return self.mat.answer
def Create(self,matrix):
zero = []
for i,m in enumerate(matrix):
for j,n in enumerate(m):
if matrix[i][j]==0:
zero.append((i,j))
self.zero = sorted(zero)
self.mat.create(matrix)
def Solve(self):
if Matrix.solve(self.mat): return True
return False
def timeSolve(self):
from time import time
t = time()
Matrix.solve(self.mat)
print(time()-t)
matrixSample = [
[8,0,0,0,0,0,0,0,0],
[0,0,3,6,0,0,0,0,0],
[0,7,0,0,9,0,2,0,0],
[0,5,0,0,0,7,0,0,0],
[0,0,0,0,4,5,7,0,0],
[0,0,0,1,0,0,0,3,0],
[0,0,1,0,0,0,0,6,8],
[0,0,8,5,0,0,0,1,0],
[0,9,0,0,0,0,4,0,0]]
代码有点繁杂,还可能有不少Bug;本人有点偏爱用推导式解决问题。但这个“数独游戏”也能够简单玩玩了,特别是批量生成数独题目特别方便。下次再补个gui界面,用键鼠来游戏操作才方便。

