前言
「 动态规划 」作为算法中一块比较野的内容,没有比较系统的分类,只能通过不断总结归纳,对各种类型进行归类。「 动态规划 」(即 Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学 以及 生物信息学中使用的,通过把原问题分解为相对简单的「 子问题 」的方式求解「 复杂问题 」的方法。
「 动态规划 」是一种算法思想:若要解一个给定问题,我们需要解其不同部分(即「 子问题 」),再根据「 子问题 」的解以得出原问题的解。要理解动态规划,就要理解 「 最优子结构 」 和 「 重复子问题 」。
本文将针对以下一些常用的动态规划问题,进行由浅入深的系统性讲解。首先来看一个简单的分类,也是今天本文要讲的内容。

直接跳到末尾 参与投票,获取粉丝专属福利。
文章目录
- 前言
- 一、递推问题
- 1、一维递推
- 2、二维递推
- 二、线性DP
- 1、最小花费
- 2、最大子段和
- 3、最长单调子序列
- 三、二维DP
- 1、最长公共子序列
- 2、最小编辑距离
- 3、双串匹配问题
- 四、记忆化搜索
- 五、背包问题
- 1、0/1 背包
- 2、完全背包
- 3、多重背包
- 4、分组背包
- 5、依赖背包
- 六、树形DP
- 七、矩阵二分
- 八、区间DP
- 九、数位DP
- 十、状态压缩DP
- 十一、斜率DP
- 十二、连通性DP
- 粉丝专属福利
一、递推问题
递推问题作为动态规划的基础,是最好掌握的,也是必须掌握的,它有点类似于高中数学中的数列,通过 前几项的值 推导出 当前项的值。
1、一维递推
你正在爬楼梯,需要 n n n 阶你才能到达楼顶。每次你可以爬 1 1 1 或 2 2 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
假设我们已经到了第
n
n
n 阶楼梯,那么它可以是从
n
−
1
n-1
n−1 阶过来的,也可以是从
n
−
2
n-2
n−2 阶过来的(但是,不可能是从
n
−
3
n-3
n−3 阶直接过来的),所以如果达到第
n
n
n 阶的方案数为
f
[
n
]
f[n]
f[n],那么到达
n
−
1
n-1
n−1 阶就是
f
[
n
−
1
]
f[n-1]
f[n−1],到达
n
−
2
n-2
n−2 阶 就是
f
[
n
−
2
]
f[n-2]
f[n−2],所以可以得出:
f
[
n
]
=
f
[
n
−
1
]
+
f
[
n
−
2
]
f[n] = f[n-1] + f[n-2]
f[n]=f[n−1]+f[n−2] 其中,当
n
=
0
n=0
n=0 时方案数为 1,代表初始情况;
n
=
1
n=1
n=1 时方案数为 1,代表走了一步,递推计算即可。
以上就是最简单的动态规划问题,也是一个经典的数列:斐波那契数列 的求解方式。它通过一个递推公式,将原本指数级的问题转化成了线性的,时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下:
int f[1000];
int climbStairs(int n){
f[0] = f[1] = 1;
for(int i = 2; i <= n; ++i) {
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
2、二维递推
给定一个非负整数 n n n,生成杨辉三角的前 n n n 行。在杨辉三角中,每个数是它 左上方 和 右上方 的数的和。
根据杨辉三角的定义,我们可以简单将上面的图进行一个变形,得到:

于是,我们可以得出以下结论:
1)杨辉三角的所有数可以存储在一个二维数组中,行代表第一维,列代表第二维度;
2)第
i
i
i 行的元素个数为
i
i
i 个;
3)第
i
i
i 行 第
j
j
j 列的元素满足公式:
c
[
i
]
[
j
]
=
{
1
i
=
0
c
[
i
−
1
]
[
j
−
1
]
+
c
[
i
−
1
]
[
j
]
o
t
h
e
r
w
i
s
e
c[i][j] = \begin{cases} 1 & i=0\\ c[i-1][j-1] + c[i-1][j] & otherwise \end{cases}
c[i][j]={1c[i−1][j−1]+c[i−1][j]i=0otherwise
于是就可以两层循环枚举了。时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
C语言代码实现如下:
int c[40];
void generate(int n) {
for(int i = 0; i < n; ++i) {
for(int j = 0; j <= i; ++j) {
if(j == 0 || j == i) {
c[i][j] = 1;
}else {
c[i][j] = c[i-1][j-1] + c[i-1][j];
}
}
}
}
二、线性DP
1、最小花费
数组的每个下标作为一个阶梯,第 i i i 个阶梯对应着一个非负数的体力花费值 c o s t [ i ] cost[i] cost[i](下标从 0 开始)。每当爬上一个阶梯,都要花费对应的体力值,一旦支付了相应的体力值,就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时,可以选择从下标为 0 0 0 或 1 1 1 的元素作为初始阶梯。
令走到第
i
i
i 层的最小消耗为
f
[
i
]
f[i]
f[i]。假设当前的位置在
i
i
i 层楼梯,那么只可能从
i
−
1
i-1
i−1 层过来,或者
i
−
2
i-2
i−2 层过来;
如果从
i
−
1
i-1
i−1 层过来,则需要消耗体力值:
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
f[i-1] + cost[i-1]
f[i−1]+cost[i−1];
如果从
i
−
2
i-2
i−2 层过来,则需要消耗体力值:
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
f[i-2] + cost[i-2]
f[i−2]+cost[i−2];
起点可以在第 0 或者 第 1 层,于是有状态转移方程:
f
[
i
]
=
{
0
i
=
0
,
1
min
(
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
,
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
)
i
>
1
f[i] = \begin{cases} 0 & i=0,1\\ \min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\end{cases}
f[i]={0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])i=0,1i>1

这个问题和一开始的递推问题的区别在于:一个是求前两项的和,一个是求最小值。这里就涉及到了动态取舍的问题,也就是动态规划的思想。
如果从前往后思考,每次都有两种选择,时间复杂度为
O
(
2
n
)
O(2^n)
O(2n)。转化成动态规划以后,只需要一个循环,时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下:
int f[1024];
int min(int a, int b) {
return a < b ? a : b;
}
int minCostClimbingStairs(int* cost, int costSize){
f[0] = 0;
f[1] = 0;
for(int i = 2; i <= costSize; ++i) {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
}
return f[costSize];
}
2、最大子段和
给定一个整数数组 n u m s nums nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
由于要求的是连续的子数组,所以对于第
i
i
i 个元素,状态转移一定是从
i
−
1
i-1
i−1 个元素转移过来的。基于这一点,可以令
f
[
i
]
f[i]
f[i] 表示以
i
i
i 号元素结尾的最大值。
那么很自然,这个最大值必然包含
n
u
m
s
[
i
]
nums[i]
nums[i] 这个元素,那么要不要包含
n
u
m
s
[
i
−
1
]
,
n
u
m
s
[
i
−
2
]
,
n
u
m
s
[
i
−
3
]
,
.
.
.
,
n
u
m
s
[
k
]
nums[i-1],nums[i-2],nums[i-3],...,nums[k]
nums[i−1],nums[i−2],nums[i−3],...,nums[k] 呢?其实就是看第
i
−
1
i-1
i−1 号元素结尾的最大值是否大于零,也就是:当
f
[
i
−
1
]
≤
0
f[i-1] \le 0
f[i−1]≤0 时,则 前
i
−
1
i-1
i−1 个元素是没必要包含进来的。所以就有状态转移方程:
f
[
i
]
=
{
n
u
m
s
[
0
]
i
=
0
n
u
m
s
[
i
]
f
[
i
−
1
]
≤
0
n
u
m
s
[
i
]
+
f
[
i
−
1
]
f
[
i
−
1
]
>
0
f[i] = \begin{cases} nums[0] & i = 0 \\ nums[i] & f[i-1] \le 0 \\ nums[i] + f[i-1] & f[i-1] > 0\end{cases}
f[i]=⎩⎪⎨⎪⎧nums[0]nums[i]nums[i]+f[i−1]i=0f[i−1]≤0f[i−1]>0一层循环枚举后,取
m
a
x
(
f
[
i
]
)
max(f[i])
max(f[i]) 就是答案了。只需要一个循环,时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下:
int dp[30010];
int max(int a, int b) {
return a > b ? a : b;
}
int maxSubArray(int* nums, int numsSize){
int maxValue = nums[0];
dp[0] = nums[0];
for(int i = 1; i < numsSize; ++i) {
dp[i] = nums[i];
if(dp[i-1] > 0) {
dp[i] += dp[i-1];
}
maxValue = max(maxValue, dp[i]);
}
return maxValue;
}
3、最长单调子序列
给定一个长度为 n ( 1 ≤ n ≤ 1000 ) n(1 \le n \le 1000) n(1≤n≤1000) 的数组 a i a_i ai,求给出它的最长递增子序列的长度。
在看这个问题之前,我们先来明确一些概念:单调序列、单调子序列、最大长单调子序列。
单调序列 就是一个满足某种单调性的数组序列,比如 单调递增序列、单调递减序列、单调不增序列、单调不减序列。举几个简单的例子:
单调递增序列:1,2,3,7,9
单调递减序列:9,8,4,2,1
单调不增序列:9,8,8,5,2
单调不减序列:1,2,2,5,5
一个比较直观的单调递增序列的例子就是一个楼梯的侧面。

我们可以把这个楼梯每一阶的高度用一个数字表示,得到一个单调递增序列,如图所示:

单调子序列 指的是任意一个数组序列,按顺序选择一些元素组成一个新的序列,并且满足单调性。对于一个长度为
n
n
n 的序列,每个元素可以选择 “取” 或者 “不取”,所以最多情况下,有
2
n
2^n
2n 个单调子序列。
如图所示,代表的是序列:[1,2,4,6,3,5,9]

其中 [1,2,6] 为它的一个长度为 3 的单调子序列,如图所示;

[1,3,6] 则不是,因为 3 和 6 的顺序不是原序列中的顺序;[1,4,3] 也不是,因为它不满足单调性。
最长单调子序列 是指对于原数组序列,能够找到的元素个数最多的单调子序列。
还是以 [1,2,4,6,3,5,9] 为例,它的最长单调子序列为:[1,2,4,6,9],长度为 5;

当然,也可以是 [1,2,3,5,9],长度同样为 5。 那么,接下来,我们看下如何通过动态规划的方法来求解 最长递增子序列。
那么,接下来,我们看下如何通过动态规划的方法来求解 最长递增子序列。
对于数组序列
a
i
(
1
≤
i
≤
n
)
a_i(1 \le i \le n)
ai(1≤i≤n),令
f
[
i
]
f[i]
f[i] 表示以第
i
i
i 个数
a
i
a_i
ai 结尾的最长递增子序列的长度。那么,我们考虑以第
i
i
i 个数
a
i
a_i
ai 结尾的最长递增子序列,它在这个序列中的前一个数一定是
a
j
(
1
≤
j
<
i
)
a_j(1 \le j < i)
aj(1≤j<i) 中的一个,所以,如果我们已经知道了
f
[
j
]
f[j]
f[j],那么就有
f
[
i
]
=
f
[
j
]
+
1
f[i] = f[j] + 1
f[i]=f[j]+1。显然,我们还需要满足
a
j
<
a
i
a_j < a_i
aj<ai 这个递增的限制条件。
那么就可以得出状态转移方程:
f
[
i
]
=
max
j
=
1
i
−
1
(
f
[
j
]
∣
a
j
<
a
i
)
+
1
f[i] = \max_{j=1}^{i-1} (f[j] \ | \ a_j < a_i) + 1
f[i]=j=1maxi−1(f[j] ∣ aj<ai)+1 这里
f
[
j
]
f[j]
f[j] 是
f
[
i
]
f[i]
f[i] 的子结构,而
m
a
x
(
f
[
j
]
)
max(f[j])
max(f[j]) 是
f
[
i
]
f[i]
f[i] 的最优子结构,当然我们需要考虑一种情况,就是没有找到最优子结构的时候,例如:
i
=
1
i=1
i=1 或者 不存在
a
j
<
a
i
a_j < a_i
aj<ai 的
j
j
j,此时
f
[
i
]
=
1
f[i] = 1
f[i]=1,表示
a
i
a_i
ai 本身是一个长度为
1
1
1 的最长递增子序列。
f
[
i
]
f[i]
f[i] 数组可以通过两层循环来求解,如下图表所示:

状态数
f
[
.
.
.
]
f[...]
f[...] 总共
O
(
n
)
O(n)
O(n) 个,状态转移的消耗为
O
(
n
)
O(n)
O(n),所以总的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2),所以对于这类问题,一般能够接受的
n
n
n 的范围在千级别,也就是
1000
,
2000
,
3000...
1000, 2000, 3000 ...
1000,2000,3000...。如果是
n
=
10000
,
100000
n=10000, 100000
n=10000,100000 的情况,就需要考虑优化了。
有关最长单调子序列的问题,还有
O
(
n
l
o
g
2
n
)
O(nlog_2n)
O(nlog2n) 的优化算法,具体方法可以参考以下文章:夜深人静写算法(二十)- 最长单调子序列。
三、二维DP
1、最长公共子序列
给定两个数组序列 a 1 , a 2 , . . . , a n a_1, a_2, ..., a_n a1,a2,...,an 和 b 1 , b 2 , . . . , b m b_1, b_2, ..., b_m b1,b2,...,bm,其中 n , m ≤ 1000 n,m \le 1000 n,m≤1000,求两个数组的最长公共子序列。
考虑两个数组序列
a
1
,
a
2
,
.
.
.
,
a
n
a_1, a_2, ..., a_n
a1,a2,...,an 和
b
1
,
b
2
,
.
.
.
,
b
m
b_1, b_2, ..., b_m
b1,b2,...,bm,对于
a
a
a 序列中第
i
i
i 个元素
a
i
a_i
ai 和
b
b
b 序列中的第
j
j
j 个元素
b
j
b_j
bj,有两种情况:
(
1
)
(1)
(1) 相等即
a
i
=
=
b
j
a_i == b_j
ai==bj 的情况,这个时候如果前缀序列
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1, a_2, ..., a_{i-1}
a1,a2,...,ai−1 和
b
1
,
b
2
,
.
.
.
,
b
j
−
1
b_1, b_2, ..., b_{j-1}
b1,b2,...,bj−1 的最长公共子序列已经求出来了,记为
x
x
x 的话,那么很显然,在两个序列分别加入
a
i
a_i
ai 和
b
j
b_j
bj 以后,长度又贡献了 1,所以
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, ..., a_{i}
a1,a2,...,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, ..., b_{j}
b1,b2,...,bj 的最长公共子序列就是
x
+
1
x+1
x+1;
 (
2
)
(2)
(2) 不相等即
a
i
≠
b
j
a_i \neq b_j
ai=bj 的情况,这个时候我们可以把问题拆分成两个更小的子问题,即 分别去掉
a
i
a_i
ai 和
b
j
b_j
bj 的情况,如图所示:
(
2
)
(2)
(2) 不相等即
a
i
≠
b
j
a_i \neq b_j
ai=bj 的情况,这个时候我们可以把问题拆分成两个更小的子问题,即 分别去掉
a
i
a_i
ai 和
b
j
b_j
bj 的情况,如图所示:

去掉
a
i
a_i
ai 以后,问题转变为求:
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1, a_2, ..., a_{i-1}
a1,a2,...,ai−1 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, ..., b_{j}
b1,b2,...,bj 的最长公共子序列;
去掉
b
j
b_j
bj 以后,问题转变为求:
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, ..., a_{i}
a1,a2,...,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
−
1
b_1, b_2, ..., b_{j-1}
b1,b2,...,bj−1 的最长公共子序列;
根据上面的两种情况的讨论,我们发现,在任何时候,我们都在求
a
a
a 的前缀 和
b
b
b 的前缀的最长公共序列,所以可以这么定义状态:用
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示
a
1
,
a
2
,
.
.
.
,
a
i
a_1, a_2, ..., a_{i}
a1,a2,...,ai 和
b
1
,
b
2
,
.
.
.
,
b
j
b_1, b_2, ..., b_{j}
b1,b2,...,bj 的最长公共子序列。
在设计状态的过程中,我们已经无形中把状态转移也设计好了,状态转移方程如下:
f
[
i
]
[
j
]
=
{
0
i
=
0
o
r
j
=
0
f
[
i
−
1
]
[
j
−
1
]
+
1
i
,
j
>
0
,
a
i
=
b
j
max
(
f
[
i
]
[
j
−
1
]
,
f
[
i
−
1
]
[
j
]
)
i
,
j
>
0
,
a
i
≠
b
j
f[i][j] = \begin{cases}0 & i=0\ or\ j=0 \\ f[i-1][j-1] + 1 & i,j>0,a_i=b_j \\ \max(f[i][j-1], f[i-1][j]) & i,j>0,a_i \neq b_j\end{cases}
f[i][j]=⎩⎪⎨⎪⎧0f[i−1][j−1]+1max(f[i][j−1],f[i−1][j])i=0 or j=0i,j>0,ai=bji,j>0,ai=bj 对于
i
=
0
i=0
i=0 或者
j
=
0
j=0
j=0 代表的是:其中一个序列的长度为 0,那么最长公共子序列的长度肯定就是 0 了;
其余两种情况,就是我们上文提到的
a
i
a_i
ai 和
b
j
b_j
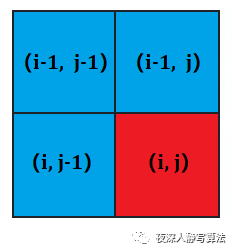
bj “相等” 与 “不相等” 的两种情况下的状态转移。如图所示,代表了字符串 “GATCGTGAGC” 和 “AGTACG” 求解最长公共子序列的
f
[
i
]
[
j
]
(
i
,
j
>
0
)
f[i][j] (i,j > 0)
f[i][j](i,j>0) 的矩阵。

对于长度分别为
n
n
n 和
m
m
m 的两个序列,求解它们的最长公共子序列时,状态数总共有
O
(
n
m
)
O(nm)
O(nm) 个,每次状态转移的消耗为
O
(
1
)
O(1)
O(1),所以总的时间复杂度为
O
(
n
m
)
O(nm)
O(nm)。
对于
f
[
i
]
[
j
]
f[i][j]
f[i][j] 这个状态,求解过程中,只依赖于
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1]、
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]、
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j]。
即每次求解只需要有 上一行 和 这一行 的状态即可,所以可以采用滚动数组进行优化,将状态转移方程变成:
f
[
c
u
r
]
[
j
]
=
{
f
[
l
a
s
t
]
[
j
−
1
]
+
1
j
>
0
,
a
i
=
b
j
max
(
f
[
c
u
r
]
[
j
−
1
]
,
f
[
l
a
s
t
]
[
j
]
)
j
>
0
,
a
i
≠
b
j
f[cur][j] = \begin{cases}f[last][j-1] + 1 & j>0,a_i=b_j \\ \max(f[cur][j-1], f[last][j]) & j>0,a_i \neq b_j\end{cases}
f[cur][j]={f[last][j−1]+1max(f[cur][j−1],f[last][j])j>0,ai=bjj>0,ai=bj 只需要简单将
i
i
i 替换成
c
u
r
cur
cur,
i
−
1
i-1
i−1 替换成
l
a
s
t
last
last 即可。这样就把原本
O
(
n
m
)
O(nm)
O(nm) 的空间复杂度变成了
O
(
p
)
O(p)
O(p),其中
p
=
min
(
n
,
m
)
p = \min(n,m)
p=min(n,m)。
- 优化后的 C++ 代码实现如下:
typedef char ValueType;
const int maxn = 5010;
int f[2][maxn];
int getLCSLength(int hsize, ValueType *h, int vsize, ValueType *v) {
memset(f, 0, sizeof(f));
int cur = 1, last = 0;
for (int i = 1; i <= vsize; ++i) {
for (int j = 1; j <= hsize; ++j) {
if (v[i] == h[j])
f[cur][j] = f[last][j - 1] + 1;
else
f[cur][j] = max(f[cur][j - 1], f[last][j]);
}
swap(last, cur);
}
return f[last][hsize];
}
有关于 最长公共子序列 的更多内容,可以参考以下内容:夜深人静写算法(二十一)- 最长公共子序列。
2、最小编辑距离
长度为 n n n 的源字符串 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,经过一些给定操作变成长度为 m m m 的目标字符串 b 1 , b 2 , . . . b m b_1,b_2,...b_m b1,b2,...bm,操作包括如下三种:
1) I n s e r t Insert Insert:在源字符串中插入一个字符,插入消耗为 I I I;
2) D e l e t e Delete Delete:在源字符串中删除一个字符,删除消耗为 D D D;
3) R e p l a c e Replace Replace:将源字符串中的一个字符替换成另一个字符,替换消耗为 R R R;
求最少的总消耗,其中 n , m ≤ 1000 n,m \le 1000 n,m≤1000。
令
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示源字符串
a
1
,
a
2
,
.
.
.
,
a
i
a_1,a_2,...,a_i
a1,a2,...,ai 经过上述三种操作变成目标字符串
b
1
,
b
2
,
.
.
.
b
j
b_1,b_2,...b_j
b1,b2,...bj 的最少消耗。
假设
a
1
,
a
2
,
.
.
.
,
a
i
a_1,a_2,...,a_{i}
a1,a2,...,ai 变成
b
1
,
b
2
,
.
.
.
b
j
−
1
b_1,b_2,...b_{j-1}
b1,b2,...bj−1 的最少消耗已经求出,等于
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1],则需要在
a
[
i
]
a[i]
a[i] 的后面插入一个字符
b
j
b_j
bj,那么产生的消耗为:
f
[
i
]
[
j
−
1
]
+
I
f[i][j-1] + I
f[i][j−1]+I 如图所示,源字符串为 “AGTA”,目标字符串为 “GATCGT” 的情况下,将源字符串变成 "“GATCG” 的最小消耗为
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1],那么只要在源字符串最后再插入一个 ‘T’,就可以把源字符串变成目标字符串 “GATCGT”;

假设
a
1
,
a
2
,
.
.
.
,
a
i
−
1
a_1,a_2,...,a_{i-1}
a1,a2,...,ai−1 变成
b
1
,
b
2
,
.
.
.
b
j
b_1,b_2,...b_{j}
b1,b2,...bj 的最少消耗已经求出,等于
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j],则需要把
a
i
a_i
ai 个删掉,那么产生的消耗为:
f
[
i
−
1
]
[
j
]
+
D
f[i-1][j] + D
f[i−1][j]+D 如图所示,源字符串为 “AGTA”,目标字符串为 “GATCGT” 的情况下,将 “AGT” 变成目标字符串的最小消耗为
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j],那么只要把源字符串最后一个’A’删掉,就可以把源字符串变成目标字符串;

假设 a 1 , a 2 , . . . , a i − 1 a_1,a_2,...,a_{i-1} a1,a2,...,ai−1 变成 b 1 , b 2 , . . . b j − 1 b_1,b_2,...b_{j-1} b1,b2,...bj−1 的最少消耗已经求出,等于 f [ i − 1 ] [ j − 1 ] f[i-1][j-1] f[i−1][j−1],则将 a i a_i ai 替换成 b j b_j bj, a 1 , a 2 , . . . , a i a_1,a_2,...,a_{i} a1,a2,...,ai 就可以变成 b 1 , b 2 , . . . b j b_1,b_2,...b_{j} b1,b2,...bj。替换时需要考虑 a i = b j a_i=b_j ai=bj 和 a i ≠ b j a_i \neq b_j ai=bj 的情况,所以替换产生的消耗为: f [ i − 1 ] [ j − 1 ] + { 0 a i = b j R a i ≠ b j f[i-1][j-1] + \begin{cases} 0 & a_i=b_j \\ R & a_i \neq b_j\end{cases} f[i−1][j−1]+{0Rai=bjai=bj 如图所示,源字符串为 “AGTA”,目标字符串为 “GATCGT” 的情况下,将 “AGT” 变成 “GATCGT” 的最小消耗为 f [ i − 1 ] [ j − 1 ] f[i-1][j-1] f[i−1][j−1],那么只要将 源字符串 的最后一个字符 替换为 目标字符串 的最后一个字符 ,就可以把源字符串变成目标字符串;替换时根据 源字符串 和 目标字符串 原本是否相等来决定消耗;

- 边界情况主要考虑以下几种:
a. 空串变成目标串 即 f [ 0 ] [ j ] f[0][j] f[0][j],总共需要插入 j j j 个字符,所以 f [ 0 ] [ j ] = f [ 0 ] [ j − 1 ] + I f[0][j] = f[0][j-1] + I f[0][j]=f[0][j−1]+I;
b. 源字符串变成空串 即 f [ i ] [ 0 ] f[i][0] f[i][0],总共需要删除 i i i 个字符,所以 f [ i ] [ 0 ] = f [ i − 1 ] [ 0 ] + D f[i][0] = f[i-1][0] + D f[i][0]=f[i−1][0]+D;
c. 空串变成空串 即 f [ 0 ] [ 0 ] = 0 f[0][0] = 0 f[0][0]=0
将上述所有状态进行一个整合,得到状态转移方程如下:
f
[
i
]
[
j
]
=
{
0
i
=
0
,
j
=
0
f
[
i
]
[
j
−
1
]
+
I
i
=
0
,
j
>
0
f
[
i
−
1
]
[
j
]
+
D
i
>
0
,
j
=
0
min
i
>
0
,
j
>
0
{
f
[
i
]
[
j
−
1
]
+
I
f
[
i
−
1
]
[
j
]
+
D
f
[
i
−
1
]
[
j
−
1
]
+
R
a
i
≠
b
j
f[i][j] = \begin{cases}0 & i=0,j=0\\f[i][j-1]+I & i=0,j>0\\ f[i-1][j] + D & i>0,j=0 \\ \min_{i>0,j>0} \begin{cases} f[i][j-1] + I\\ f[i-1][j] + D\\ f[i-1][j-1] + R_{a_i \neq b_j}\end{cases}\end{cases}
f[i][j]=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧0f[i][j−1]+If[i−1][j]+Dmini>0,j>0⎩⎪⎨⎪⎧f[i][j−1]+If[i−1][j]+Df[i−1][j−1]+Rai=bji=0,j=0i=0,j>0i>0,j=0
通过这个状态矩阵,最后计算得到
f
[
n
]
[
m
]
f[n][m]
f[n][m] 就是该题所求 "源字符串
a
1
,
a
2
,
.
.
.
,
a
n
a_1,a_2,...,a_n
a1,a2,...,an,经过 插入、删除、替换 变成目标字符串
b
1
,
b
2
,
.
.
.
b
m
b_1,b_2,...b_m
b1,b2,...bm" 的最少消耗了,特殊的,当
I
=
D
=
R
=
1
I = D = R = 1
I=D=R=1 时,
f
[
n
]
[
m
]
f[n][m]
f[n][m] 就是字符串
a
a
a 和
b
b
b 的莱文斯坦距离。
状态总数
O
(
n
m
)
O(nm)
O(nm),每次状态转移的消耗为
O
(
1
)
O(1)
O(1),所以总的时间复杂度为
O
(
n
m
)
O(nm)
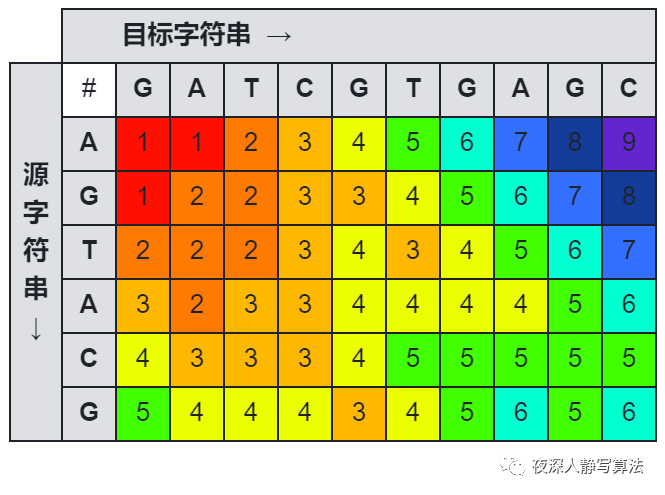
O(nm),空间上可以采用滚动数组进行优化,具体优化方案可以参考 最长公共子序列 的求解过程。
如图所示的是一张源字符串 “AGTACG” 到目标字符串 “GATCGTGAGC” 的莱文斯坦距离图。
有关最小编辑距离的详细内容,可以参考:夜深人静写算法(二十二)- 最小编辑距离。
3、双串匹配问题
给定一个 匹配字符串 s (只包含小写字母) 和一个 模式字符串 p (包含小写字母和两种额外字符:
'.'和'*'),要求实现一个支持'.'和'*'的正则表达式匹配('*'前面保证有字符)。
'.'匹配任意单个字符
'*'匹配零个或多个前面的那一个元素
这是个经典的 串匹配 问题,可以按照 最长公共子序列 的思路去解决。令
f
(
i
,
j
)
f(i, j)
f(i,j) 代表的是 匹配串前缀 s[0:i] 和 模式串前缀 p[0:j] 是否有匹配,只有两个值: 0 代表 不匹配, 1 代表 匹配。
于是,对模式串进行分情况讨论:
1)当 p[j] 为.时,代表 s[i] 为任意字符时,它都能够匹配(没毛病吧?没毛病),所以问题就转化成了求 匹配串前缀 s[0:i-1] 和 模式串前缀 p[0:j-1] 是否有匹配的问题,也就是这种情况下
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
f(i, j) = f(i-1, j-1)
f(i,j)=f(i−1,j−1),如图1所示:

2)当 p[j] 为*时,由于*前面保证有字符,所以拿到字符 p[j-1],分情况讨论:
2.a)如果 p[j-1] 为.时,可以匹配所有 s[0:i] 的后缀,这种情况下,只要
f
(
k
,
j
−
2
)
f(k, j-2)
f(k,j−2) 为 1,
f
(
i
,
j
)
f(i, j)
f(i,j) 就为 1;其中
k
∈
[
0
,
i
]
k \in [0, i]
k∈[0,i]。如下图所示:

2.b)如果 p[j-1] 非.时,只有当 s[0:i] 的后缀 字符全为 p[j-1] 时,才能去匹配 s[0:i] 的前缀,同样转化成
f
(
k
,
j
−
2
)
f(k, j-2)
f(k,j−2) 的子问题。如下图所示:

3)当 p[j] 为其他任意字符时,一旦 p[j] 和 s[i] 不匹配,就认为
f
(
i
,
j
)
=
0
f(i, j) = 0
f(i,j)=0,否则
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
f(i, j) = f(i-1, j-1)
f(i,j)=f(i−1,j−1),如下图所示:

最后,这个问题可以采用 记忆化搜索 求解,并且需要考虑一些边界条件,边界条件可以参考代码实现中的讲解。记忆化搜索会在下文仔细讲解。
匹配串的长度为
n
n
n,模式串的长度为
m
m
m。状态数:
O
(
n
m
)
O(nm)
O(nm),状态转移:
O
(
n
)
O(n)
O(n),时间复杂度:
O
(
n
2
m
)
O(n^2m)
O(n2m)。
四、记忆化搜索
给定一个 n ( n ≤ 45 ) n(n \le 45) n(n≤45),求 斐波那契数列的第 n n n 项的值,要求用递归实现。
那么,我们只需要套用上面的递归函数,并且处理好递归出口,就能把它写成递归的形式,C语言 代码实现如下:
int f(unsigned int n) {
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
递归求解的过程如下:

这是一棵二叉树,树的高度为
n
n
n,所以粗看递归访问时结点数为
2
n
2^n
2n,但是仔细看,对于任何一棵子树而言,左子树的高度一定比右子树的高度大,所以不是一棵严格的完全二叉树。为了探究它实际的时间复杂度,我们改下代码:
int f(unsigned int n) {
++c[n];
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
加了一句代码 ++c[n];,引入一个计数器,来看下在不同的
n
n
n 的情况下,
f
(
n
)
f(n)
f(n) 这个函数的调用次数,如图所示:
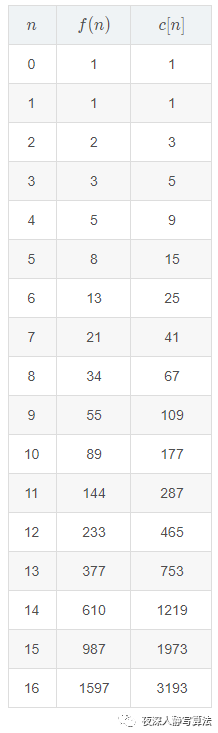
观察
c
[
n
]
c[n]
c[n] 的增长趋势,首先排除等差数列,然后再来看是否符合等比数列,我们来尝试求下
c
[
n
]
/
c
[
n
−
1
]
c[n] / c[n-1]
c[n]/c[n−1] 的值,列出表格如下:

观察发现,随着
n
n
n 的不断增大,
c
[
n
]
/
c
[
n
−
1
]
c[n]/c[n-1]
c[n]/c[n−1] 越来越接近一个常数,而这个常数就是黄金分割的倒数:
2
5
−
1
≈
1.618034
\frac {2}{ \sqrt 5 - 1} \approx 1.618034
5
−12≈1.618034 当
n
n
n 趋近于无穷大的时候,满足如下公式:
c
[
n
]
=
2
5
−
1
c
[
n
−
1
]
c[n] = \frac {2}{ \sqrt 5 - 1} c[n-1]
c[n]=5
−12c[n−1] 对等比数列化解后累乘得到:
c
[
n
]
=
2
5
−
1
c
[
n
−
1
]
=
(
2
5
−
1
)
2
c
[
n
−
2
]
=
(
2
5
−
1
)
n
\begin{aligned}c[n] &= \frac {2}{ \sqrt 5 - 1} c[n-1]\\ &= (\frac {2}{ \sqrt 5 - 1})^2 c[n-2]\\ &= (\frac {2}{ \sqrt 5 - 1})^n \end{aligned}
c[n]=5
−12c[n−1]=(5
−12)2c[n−2]=(5
−12)n 所以,斐波那契数列递归求解的时间复杂度就是 :
O
(
(
2
5
−
1
)
n
)
O((\frac {2}{ \sqrt 5 - 1})^n)
O((5
−12)n)
这是一个指数级的算法,随着
n
n
n 的不断增大,时间消耗呈指数级增长,我们在写代码的时候肯定是要避免这样的写法的,尤其是在服务器开发过程中,CPU 是一种极其宝贵的资源,任何的浪费都是可耻的。但是,面试官又要求用递归实现,真是太讨厌了!
那么,怎么来优化这里的算力消耗呢?
递归求解斐波那契数列其实是一个深度优先搜索的过程,它是毫无优化的暴力枚举,对于
f
(
5
)
f(5)
f(5) 的求解,如图所示:

同时,我们也发现,计算过程中其实有很多重叠子问题,例如
f
(
3
)
f(3)
f(3) 被计算了
2
2
2 次,如图所示:

f
(
2
)
f(2)
f(2) 被计算了
3
3
3 次,如图所示:
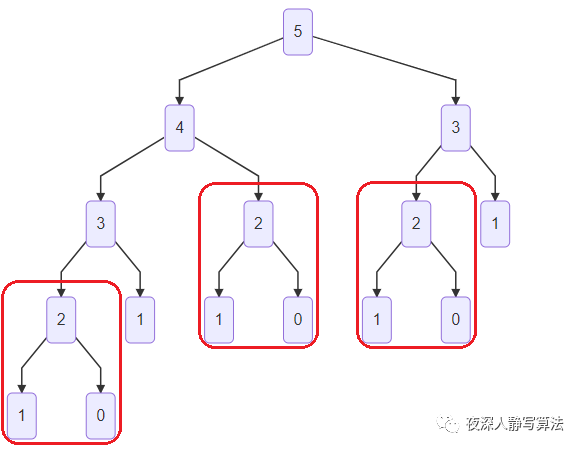
所以如果我们能够确保每个
f
(
i
)
f(i)
f(i) 只被计算一次,问题就迎刃而解了。可以考虑将
f
(
i
)
f(i)
f(i) 计算出来的值存储到哈希数组
h
[
i
]
h[i]
h[i] 中,当第二次要访问
f
(
i
)
f(i)
f(i) 时,直接取
h
[
i
]
h[i]
h[i] 的值即可,这样每次计算
f
(
i
)
f(i)
f(i) 的时间复杂度变成了
O
(
1
)
O(1)
O(1),总共需要计算
f
(
2
)
,
f
(
3
)
,
.
.
.
f
(
n
)
f(2),f(3),...f(n)
f(2),f(3),...f(n),总的时间复杂度就变成了
O
(
n
)
O(n)
O(n) 。
这种用哈希数组来记录运算结果,避免重复运算的方法就是记忆化搜索。
这件事情如何执行下去呢?
我们用一个数组
h
[
i
]
h[i]
h[i] 来记录 斐波那契数列 第
i
i
i 项的值,把之前的递归代码改成如下形式:
const int inf = -1;
int h[46];
void init() {
memset(h, inf, sizeof(h)); // 1)
}
int f(unsigned int n) {
if(n <= 1) {
return 1;
}
int &fib = h[n]; // 2)
if(fib != inf) {
return fib; // 3)
}
fib = f(n-1) + f(n-2); // 4)
return fib;
}
- 1)初始化所有
f
(
i
)
f(i)
f(i) 都没有被计算过,为了方便用
memset,可以将inf定义成 -1; - 2)注意这里用了个引用,而且一定要用引用,具体原因留给读者自己思考,当然不想思考的话,下文也会讲到,不必担心;
- 3)当
fib也就是h[n]已经计算过了,那么直接返回结果即可; - 4)最后,利用递归计算
h[n]的值,并且返回结果;
和递归版本相比,多了这么一段代码:
int &fib = h[n];
if(fib != inf) {
return fib;
}
那么它的作用体现在哪里呢?我们通过一个动图来感受一下:

如图所示,当第二次需要计算
f
(
2
)
f(2)
f(2) 和
f
(
3
)
f(3)
f(3) 时,由于结果已经计算出来并且存储在
h
[
2
]
h[2]
h[2] 和
h
[
3
]
h[3]
h[3] 中,所以上面这段代码的fib != inf表达式为真,直接返回,不再需要往下递归计算,这样就把原本的 “递归二叉树” 转换成了 “递归链”, 从而将原本指数级的算法变成了多项式级别。
上文用一个简单的例子阐述了记忆化搜索的实现方式,并且提到了利用数组来记录已经计算出来的重叠子问题,这个和动态规划的思想非常相似,没错,记忆化搜索其实用的就是动态规划的思想。更加确切的说,可以用如下公式来表示:
有关记忆化搜索的更多内容,可以参考: 夜深人静写算法(二十六)- 记忆化搜索。
五、背包问题
1、0/1 背包
有 n ( n ≤ 100 ) n(n \le100) n(n≤100) 个物品和一个容量为 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 的背包。第 i i i 个物品的容量是 c [ i ] c[i] c[i],价值是 w [ i ] w[i] w[i]。现在需要选择一些物品放入背包,并且总容量不能超过背包容量,求能够达到的物品的最大总价值。
以上就是 0/1 背包问题的完整描述,之所以叫 0/1 背包,是因为每种物品只有一个,可以选择放入背包或者不放,而 0 代表不放,1 代表放。
第一步:设计状态;
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 个物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m]);
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值,即前
i
i
i 个物品恰好放入容量为
j
j
j 的背包所得到的最大总价值;
第二步:列出状态转移方程;
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
)
dp[i][j] = max(dp[i-1][j], dp[i-1][j - c[i]] + w[i])
dp[i][j]=max(dp[i−1][j],dp[i−1][j−c[i]]+w[i]) 因为每个物品要么放,要么不放,所以只需要考虑第
i
i
i 个物品 放 或 不放 的情况:
1)不放:如果 “第
i
i
i 个物品不放入容量为
j
j
j 的背包”,那么问题转化成求 “前
i
−
1
i-1
i−1 个物品放入容量为
j
j
j 的背包” 的问题;由于不放,所以最大价值就等于 “前
i
−
1
i-1
i−1 个物品放入容量为
j
j
j 的背包” 的最大价值,即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j];
2)放:如果 “第
i
i
i 个物品放入容量为
j
j
j 的背包”,那么问题转化成求 “前
i
−
1
i-1
i−1 个物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的问题;那么此时最大价值就等于 “前
i
−
1
i-1
i−1 个物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的最大价值 加上放入第
i
i
i 个物品的价值,即
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
dp[i-1][j - c[i]] + w[i]
dp[i−1][j−c[i]]+w[i];
将以上两种情况取大者,就是我们所求的 “前
i
i
i 个物品恰好放入容量为
j
j
j 的背包” 的最大价值了。
 我们发现,当状态在进行转移的时候,
(
i
,
j
)
(i, j)
(i,j) 不是来自
(
i
−
1
,
j
)
(i-1, j)
(i−1,j),就是来自
(
i
−
1
,
j
−
c
[
i
]
)
(i-1, j - c[i])
(i−1,j−c[i]),所以必然有一个初始状态,而这个初始状态就是
(
0
,
0
)
(0, 0)
(0,0),含义是 “前 0 个物品放入一个背包容量为 0 的背包”,这个状态下的最大价值为 0,即
d
p
[
0
]
[
0
]
=
0
dp[0][0] = 0
dp[0][0]=0;
我们发现,当状态在进行转移的时候,
(
i
,
j
)
(i, j)
(i,j) 不是来自
(
i
−
1
,
j
)
(i-1, j)
(i−1,j),就是来自
(
i
−
1
,
j
−
c
[
i
]
)
(i-1, j - c[i])
(i−1,j−c[i]),所以必然有一个初始状态,而这个初始状态就是
(
0
,
0
)
(0, 0)
(0,0),含义是 “前 0 个物品放入一个背包容量为 0 的背包”,这个状态下的最大价值为 0,即
d
p
[
0
]
[
0
]
=
0
dp[0][0] = 0
dp[0][0]=0;
那么我们再来考虑,
(
0
,
3
)
(0, 3)
(0,3) 是什么意思呢?它代表的是 “前 0 个物品恰好放入一个背包容量为 3 的背包”,明显这种情况是不存在的,因为 0 个物品的价值肯定是 0。所以这种状态被称为非法状态,非法状态是无法进行状态转移的,于是我们可以通过初始状态和非法状态进所有状态进行初始化。
d
p
[
0
]
[
i
]
=
{
0
i
=
0
i
n
f
i
>
0
dp[0][i] = \begin{cases} 0 & i = 0\\ inf & i > 0\end{cases}
dp[0][i]={0infi=0i>0
其中
i
n
f
inf
inf 在程序实现时,我们可以设定一个非常小的数,比如
−
1000000000
-1000000000
−1000000000,只要保证无论如何状态转移它都不能成为最优解的候选状态。为了加深状态转移的概念,来看图二-5-1 的一个例子,每个格子代表一个状态,
(
0
,
0
)
(0,0)
(0,0) 代表初始状态,蓝色的格子代表已经求得的状态,灰色的格子代表非法状态,红色的格子代表当前正在进行转移的状态,图中的第
i
i
i 行代表了前
i
i
i 个物品对应容量的最优值,第 4 个物品的容量为 2,价值为 8,则有状态转移如下:
d
p
[
4
]
[
4
]
=
m
a
x
(
d
p
[
4
−
1
]
[
4
]
,
d
p
[
4
−
1
]
[
4
−
2
]
+
8
)
=
m
a
x
(
d
p
[
3
]
[
4
]
,
d
p
[
3
]
[
2
]
+
8
)
\begin{aligned} dp[4][4] &= max( dp[4-1][4], dp[4-1][4 - 2] + 8) \\ &= max( dp[3][4], dp[3][2] + 8) \end{aligned}
dp[4][4]=max(dp[4−1][4],dp[4−1][4−2]+8)=max(dp[3][4],dp[3][2]+8)

有关 0/1 背包的更多内容,可以参考:夜深人静写算法(十四)- 0/1 背包。
2、完全背包
有 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 种物品和一个容量为 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 的背包。第 i i i 种物品的容量是 c [ i ] c[i] c[i],价值是 w [ i ] w[i] w[i]。现在需要选择一些物品放入背包,每种物品可以无限选择,并且总容量不能超过背包容量,求能够达到的物品的最大总价值。
以上就是完全背包问题的完整描述,和 0/1 背包的区别就是每种物品可以无限选取,即文中红色字体标注的内容;
第一步:设计状态;
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 种物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m]);
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值,即前
i
i
i 种物品(每种物品可以选择无限件)恰好放入容量为
j
j
j 的背包所得到的最大总价值;
第二步:列出状态转移方程; d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j − c [ i ] ∗ k ] + w [ i ] ∗ k ) dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k) dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k) ( 0 ≤ k ≤ j c [ i ] ) (0 \le k \le \frac {j} {c[i]}) (0≤k≤c[i]j)
- 因为每种物品有无限种可放置,将它归类为以下两种情况:
1)不放:如果 “第 i i i 种物品不放入容量为 j j j 的背包”,那么问题转化成求 “前 i − 1 i-1 i−1 种物品放入容量为 j j j 的背包” 的问题;由于不放,所以最大价值就等于 “前 i − 1 i-1 i−1 种物品放入容量为 j j j 的背包” 的最大价值,对应状态转移方程中 k = 0 k = 0 k=0 的情况, 即 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j];
2)放 k 个:如果 “第 i i i 种物品放入容量为 j j j 的背包”,那么问题转化成求 “前 i − 1 i-1 i−1 种物品放入容量为 j − c [ i ] ∗ k j-c[i]*k j−c[i]∗k 的背包” 的问题;那么此时最大价值就等于 “前 i − 1 i-1 i−1 种物品放入容量为 j − c [ i ] ∗ k j-c[i]*k j−c[i]∗k 的背包” 的最大价值 加上放入 k k k 个第 i i i 种物品的价值,即 d p [ i − 1 ] [ j − c [ i ] ∗ k ] + w [ i ] ∗ k dp[i-1][j - c[i]*k] + w[i]*k dp[i−1][j−c[i]∗k]+w[i]∗k;
枚举所有满足条件的 k k k 就是我们所求的 “前 i i i 种物品恰好放入容量为 j j j 的背包” 的最大价值了。注意:由于每件物品都可以无限选择,所以这里描述的时候都是用的 “种” 作为单位,即代表不同种类的物品。
对于 n n n 种物品放入一个容量为 m m m 的背包,状态数为 O ( n m ) O(nm) O(nm),每次状态转移的消耗为 O ( k ) O(k) O(k),所以整个状态转移的过程时间复杂度是大于 O ( n m ) O(nm) O(nm) 的,那么实际是多少呢?考虑最坏情况下,即 c [ i ] = 1 c[i] = 1 c[i]=1 时,那么要计算的 d p [ i ] [ j ] dp[i][j] dp[i][j] 的转移数为 j j j,总的状态转移次数就是 m ( m + 1 ) 2 \frac {m(m + 1)} {2} 2m(m+1),所以整个算法的时间复杂度是 O ( n m 2 ) O(nm^2) O(nm2) 的,也就是说状态转移均摊时间复杂度是 O ( m ) O(m) O(m) 的。
我们把状态转移方程进行展开后得到如下的
k
+
1
k+1
k+1 个式子:
d
p
[
i
]
[
j
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
+
w
[
i
]
∗
2
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
k
(
k
+
1
)
dp[i][j] = max \begin{cases} dp[i-1][j] & (1)\\ dp[i-1][j - c[i]] + w[i] & (2)\\ dp[i-1][j - c[i]*2] + w[i]*2 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *k & (k+1) \end{cases}
dp[i][j]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j]dp[i−1][j−c[i]]+w[i]dp[i−1][j−c[i]∗2]+w[i]∗2...dp[i−1][j−c[i]∗k]+w[i]∗k(1)(2)(3)(k+1)
利用待定系数法,用
j
−
c
[
i
]
j-c[i]
j−c[i] 代替上式的
j
j
j 得到如下式子:
d
p
[
i
]
[
j
−
c
[
i
]
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
+
w
[
i
]
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
3
]
+
w
[
i
]
∗
2
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
(
k
−
1
)
(
k
)
dp[i][j-c[i]] = max \begin{cases} dp[i-1][j-c[i]] & (1)\\ dp[i-1][j - c[i]*2] + w[i] & (2)\\ dp[i-1][j - c[i]*3] + w[i]*2 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *(k-1) & (k) \end{cases}
dp[i][j−c[i]]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j−c[i]]dp[i−1][j−c[i]∗2]+w[i]dp[i−1][j−c[i]∗3]+w[i]∗2...dp[i−1][j−c[i]∗k]+w[i]∗(k−1)(1)(2)(3)(k)
等式两边都加上
w
[
i
]
w[i]
w[i] 得到:
d
p
[
i
]
[
j
−
c
[
i
]
]
+
w
[
i
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
(
1
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
2
]
+
w
[
i
]
∗
2
(
2
)
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
3
]
+
w
[
i
]
∗
3
(
3
)
.
.
.
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
k
(
k
)
dp[i][j-c[i]] + w[i] = max \begin{cases} dp[i-1][j-c[i]] + w[i] & (1)\\ dp[i-1][j - c[i]*2] + w[i]*2 & (2)\\ dp[i-1][j - c[i]*3] + w[i]*3 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *k & (k) \end{cases}
dp[i][j−c[i]]+w[i]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j−c[i]]+w[i]dp[i−1][j−c[i]∗2]+w[i]∗2dp[i−1][j−c[i]∗3]+w[i]∗3...dp[i−1][j−c[i]∗k]+w[i]∗k(1)(2)(3)(k)
于是我们发现,这里的
(
1
)
.
.
.
(
k
)
(1)...(k)
(1)...(k) 式子等价于最开始的状态转移方程中的
(
2
)
.
.
.
(
k
+
1
)
(2) ... (k+1)
(2)...(k+1) 式,所以原状态转移方程可以简化为:
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
]
[
j
−
c
[
i
]
]
+
w
[
i
]
)
dp[i][j] = max(dp[i-1][j], dp[i][j-c[i]] + w[i])
dp[i][j]=max(dp[i−1][j],dp[i][j−c[i]]+w[i])
这样就把原本均摊时间复杂度为
O
(
m
)
O(m)
O(m) 的状态转移优化到了
O
(
1
)
O(1)
O(1)。
那么我们来理解一下这个状态转移方程的含义:对于第
i
i
i 种物品,其实只有两种选择:一个都不放、至少放一个;一个都不放 就是 “前
i
−
1
i-1
i−1 种物品放满一个容量为
j
j
j 的背包” 的情况,即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j];至少放一个 的话,我们尝试在 “前
i
i
i 种物品放满一个容量为
j
j
j 的背包” 里拿掉 1 个物品,即 “前
i
i
i 种物品放满一个容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包”,这时候的值就是
d
p
[
i
]
[
j
−
c
[
i
]
]
+
w
[
i
]
dp[i][j-c[i]] + w[i]
dp[i][j−c[i]]+w[i]。取两者的大者就是答案了。
其实这个思路我可以在本文开头就讲,也容易理解,之所以引入优化以及逐步推导的过程,就是想告诉读者,很多动态规划的问题是不能套用模板的,从简单的思路出发,加上一些推导和优化,逐步把复杂的问题循序渐进的求出来,才是解决问题的普遍思路。
有关完全背包的更多内容,可以参考:夜深人静写算法(十五)- 完全背包。
3、多重背包
有 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 种物品和一个容量为 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 的背包。第 i i i 种物品的容量是 c [ i ] c[i] c[i],价值是 w [ i ] w[i] w[i]。现在需要选择一些物品放入背包,每种物品可以选择 x [ i ] x[i] x[i] 件,并且总容量不能超过背包容量,求能够达到的物品的最大总价值。
以上就是多重背包问题的完整描述,和 0/1 背包、完全背包的区别就是每种物品的选取有物品自己的值域限制,即文中红色字体标注的内容;
第一步:设计状态;
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 种物品恰好放入容量为
j
j
j 的背包
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m]);
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下该背包得到的最大价值,即前
i
i
i 种物品(每种物品可以选择
x
[
i
]
x[i]
x[i] 件)恰好放入容量为
j
j
j 的背包所得到的最大总价值;
第二步:列出状态转移方程;
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
k
)
(
0
≤
k
≤
x
[
i
]
)
dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k) \\ (0 \le k \le x[i])
dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k)(0≤k≤x[i]) 因为每种物品有
x
[
i
]
x[i]
x[i] 种可放置,将它归类为以下两种情况:
1)不放:如果 “第
i
i
i 种物品不放入容量为
j
j
j 的背包”,那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的问题;由于不放,所以最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
j
j 的背包” 的最大价值,对应状态转移方程中
k
=
0
k = 0
k=0 的情况, 即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j];
2)放 k 个:如果 “第
i
i
i 种物品放入容量为
j
j
j 的背包”,那么问题转化成求 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的问题;那么此时最大价值就等于 “前
i
−
1
i-1
i−1 种物品放入容量为
j
−
c
[
i
]
∗
k
j-c[i]*k
j−c[i]∗k 的背包” 的最大价值 加上放入
k
k
k 个第
i
i
i 种物品的价值,即
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
k
dp[i-1][j - c[i]*k] + w[i]*k
dp[i−1][j−c[i]∗k]+w[i]∗k;
枚举所有满足条件的
k
k
k 就是我们所求的 “前
i
i
i 种物品恰好放入容量为
j
j
j 的背包” 的最大价值了。
多重背包问题是背包问题的一般情况,每种物品有自己的值域限制。如果从状态转移方程出发,我们可以把三种背包问题进行归纳统一,得到一个统一的状态转移方程如下:
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
−
c
[
i
]
∗
k
]
+
w
[
i
]
∗
k
)
dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i]*k)
dp[i][j]=max(dp[i−1][j−c[i]∗k]+w[i]∗k) 对于 0/1 背包问题,
k
k
k 的取值为
0
,
1
0,1
0,1;
对于完全背包问题,
k
k
k 的取值为
0
,
1
,
2
,
3
,
.
.
.
,
⌊
j
c
[
i
]
⌋
0, 1, 2, 3, ..., \lfloor \frac j {c[i]} \rfloor
0,1,2,3,...,⌊c[i]j⌋;
对于多重背包问题,
k
k
k 的取值为
0
,
1
,
2
,
3
,
.
.
.
,
x
[
i
]
0, 1, 2, 3, ..., x[i]
0,1,2,3,...,x[i];
对于
n
n
n 种物品放入一个容量为
m
m
m 的背包,状态数为
O
(
n
m
)
O(nm)
O(nm),每次状态转移的消耗为
O
(
x
[
i
]
)
O(x[i])
O(x[i]),所以整个状态转移的过程时间复杂度是大于
O
(
n
m
)
O(nm)
O(nm) 的,那么实际是多少呢?
考虑最坏情况下,即
x
[
i
]
=
m
x[i] = m
x[i]=m 时,那么要计算的
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 的转移数为
j
j
j,总的状态转移次数就是
m
(
m
+
1
)
2
\frac {m(m + 1)} {2}
2m(m+1),所以整个算法的时间复杂度是
O
(
n
m
2
)
O(nm^2)
O(nm2) 的,也就是说状态转移均摊时间复杂度是
O
(
m
)
O(m)
O(m) 的。
一个容易想到的优化是:我们可以将每种物品拆成
x
[
i
]
x[i]
x[i] 个,这样变成了
∑
i
=
1
n
x
[
i
]
\sum_{i=1}^n x[i]
∑i=1nx[i] 个物品的 0/1 背包问题,我们知道 0/1 背包问题优化完以后,空间复杂度只和容量有关,即
O
(
m
)
O(m)
O(m)。
所以多重背包问题的空间复杂度至少是可以优化到
O
(
m
)
O(m)
O(m) 的。
然而, 如果这样拆分,时间复杂度还是没有变化,但是给我们提供了一个思路,就是每种物品是可以拆分的。假设有
x
[
i
]
x[i]
x[i] 个物品,我们可以按照 2 的幂进行拆分,把它拆分成:
1
,
2
,
4
,
.
.
.
,
2
k
−
1
,
x
[
i
]
−
2
k
+
1
1, 2, 4, ..., 2^{k-1}, x[i] - 2^{k} + 1
1,2,4,...,2k−1,x[i]−2k+1
其中
k
k
k 是最大的满足
x
[
i
]
−
2
k
+
1
≥
0
x[i] - 2^{k} + 1 \ge 0
x[i]−2k+1≥0 的非负整数。
这样,1 到
x
[
i
]
x[i]
x[i] 之间的所有整数都能通过以上
k
+
1
k+1
k+1 个数字组合出来,所以只要拆成以上
k
+
1
k+1
k+1 个物品,所有取
k
(
0
≤
k
≤
x
[
i
]
)
k (0 \le k \le x[i])
k(0≤k≤x[i]) 个物品的情况都能被考虑进来。
举例说明,当
x
[
i
]
=
14
x[i] = 14
x[i]=14 时,可以拆分成 1,2,4,7 个物品,那么当我们要取 13 个这类物品的时候,相当于选择 2、4、7,容量分别为
c
[
i
]
∗
2
,
c
[
i
]
∗
4
,
c
[
i
]
∗
7
c[i]*2, c[i]*4, c[i]* 7
c[i]∗2,c[i]∗4,c[i]∗7, 价值分别为
w
[
i
]
∗
2
,
w
[
i
]
∗
4
,
w
[
i
]
∗
7
w[i]*2, w[i]*4, w[i]* 7
w[i]∗2,w[i]∗4,w[i]∗7。
通过这种拆分方式,
x
[
i
]
x[i]
x[i] 最多被拆分成
l
o
g
2
x
[
i
]
log_2 {x[i]}
log2x[i] 个物品,然后再用 0/1 背包求解,得到了一个时间复杂度为
O
(
m
∑
i
=
1
n
l
o
g
2
x
[
i
]
)
O(m\sum_{i=1}^{n}log_2{x[i]})
O(m∑i=1nlog2x[i]) 的算法。
有关多重背包的更多内容,可以参考:夜深人静写算法(十六)- 多重背包。
4、分组背包
有 n ( n ≤ 1000 ) n(n \le 1000) n(n≤1000) 个物品和一个容量为 m ( m ≤ 1000 ) m(m \le 1000) m(m≤1000) 的背包。这些物品被分成若干组,第 i i i 个物品属于 g [ i ] g[i] g[i] 组,容量是 c [ i ] c[i] c[i],价值是 w [ i ] w[i] w[i],现在需要选择一些物品放入背包,并且每组最多放一个物品,总容量不能超过背包容量,求能够达到的物品的最大总价值。
以上就是分组背包问题的完整描述,和其它背包问题的区别就是每个物品多了一个组号,并且相同组内,最多只能选择一个物品放入背包;因为只有一个物品,所以读者可以暂时忘掉 完全背包 和 多重背包 的概念,在往下看之前,先回忆一下 0/1 背包的状态转移方程。
第一步:预处理;
首先把每个物品按照组号
g
[
i
]
g[i]
g[i] 从小到大排序,假设总共有
t
t
t 组,则将
g
[
i
]
g[i]
g[i] 按顺序离散到
[
1
,
t
]
[1,t]
[1,t] 的正整数。这样做的目的是为了将
g
[
i
]
g[i]
g[i] 作为下标映射到状态数组中;

第二步:设计状态;
状态
(
k
,
j
)
(k, j)
(k,j) 表示前
k
k
k 组物品恰好放入容量为
j
j
j 的背包
(
k
∈
[
0
,
t
]
,
j
∈
[
0
,
m
]
)
(k \in [0, t], j \in [0, m])
(k∈[0,t],j∈[0,m]);令
d
p
[
k
]
[
j
]
dp[k][j]
dp[k][j] 表示状态
(
k
,
j
)
(k, j)
(k,j) 下该背包得到的最大价值,即前
k
k
k 组物品(每组物品至多选一件)恰好放入容量为
j
j
j 的背包所得到的最大总价值;
第三步:列出状态转移方程:
d
p
[
k
]
[
j
]
=
m
a
x
(
d
p
[
k
−
1
]
[
j
]
,
d
p
[
k
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
)
dp[k][j] = max(dp[k-1][j], dp[k-1][j - c[i]] + w[i])
dp[k][j]=max(dp[k−1][j],dp[k−1][j−c[i]]+w[i])
k
=
g
[
i
]
k = g[i]
k=g[i]因为每个物品有只有两种情况:
1)不放:如果 “第
i
i
i 个物品(属于第
k
k
k 组)不放入容量为
j
j
j 的背包”,那么问题转化成求 “前
k
−
1
k-1
k−1 组物品放入容量为
j
j
j 的背包” 的问题;由于不放,所以最大价值就等于 “前
k
−
1
k-1
k−1 组物品放入容量为
j
j
j 的背包” 的最大价值,对应状态转移方程中的
d
p
[
k
−
1
]
[
j
]
dp[k-1][j]
dp[k−1][j];
2)放:如果 “第
i
i
i 个物品(属于第
k
k
k 组)放入容量为
j
j
j 的背包”,那么问题转化成求 “前
k
−
1
k-1
k−1 组物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的问题;那么此时最大价值就等于 “前
k
−
1
k-1
k−1 组物品放入容量为
j
−
c
[
i
]
j-c[i]
j−c[i] 的背包” 的最大价值 加上放入第
i
i
i 个物品的价值,即
d
p
[
k
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
dp[k-1][j - c[i]] + w[i]
dp[k−1][j−c[i]]+w[i];
因为 前
k
−
1
k-1
k−1 组物品中一定不存在第
k
k
k 组中的物品,所以能够满足 “最多放一个” 这个条件;
对于
n
n
n 个物品放入一个容量为
m
m
m 的背包,状态数为
O
(
n
m
)
O(nm)
O(nm),每次状态转移的消耗为
O
(
1
)
O(1)
O(1),所以整个状态转移的过程时间复杂度是
O
(
n
m
)
O(nm)
O(nm);
注意在分组背包求解的时候,要保证相同组的在一起求,而一开始的预处理和离散化正式为了保证这一点,这样,每个物品的组号为
g
[
i
]
=
1
,
2
,
3
,
4...
,
t
g[i] = 1,2,3,4...,t
g[i]=1,2,3,4...,t,并且我们可以把状态转移方程进一步表示成和
k
k
k 无关的,如下:
d
p
[
g
[
i
]
]
[
j
]
=
m
a
x
(
d
p
[
g
[
i
]
−
1
]
[
j
]
,
d
p
[
g
[
i
]
−
1
]
[
j
−
c
[
i
]
]
+
w
[
i
]
)
dp[ g[i] ][j] = max(dp[ g[i]-1][j], dp[ g[i]-1][j - c[i]] + w[i])
dp[g[i]][j]=max(dp[g[i]−1][j],dp[g[i]−1][j−c[i]]+w[i])
有关分组背包更加详细的内容,可以参考:夜深人静写算法(十七)- 分组背包。
5、依赖背包
商店里有 n ( n ≤ 50 ) n(n \le 50) n(n≤50) 个盒子,每个盒子价钱为 p [ i ] ( p [ i ] ≤ 1000 ) p[i](p[i] \le 1000) p[i](p[i]≤1000),价值为 0,盒子里面有一些小礼物,数量为 m [ i ] ( 1 ≤ m [ i ] ≤ 10 ) m[i](1 \le m[i] \le 10) m[i](1≤m[i]≤10),每个小礼物描述成一个二元组 ( c , v ) (c, v) (c,v), c c c 为价钱, v v v 为价值,如果要买小礼物,必须先买盒子。现在给出价钱 m ( m ≤ 100000 ) m(m \le 100000) m(m≤100000),求能够买到的最大价值。
这是一个比较特殊的依赖性背包问题,也是依赖背包中最简单的情况,其中盒子作为 主件,小礼物作为 附件。想要购买附件,必须先购买主件,此所谓 “依赖” ;
第一步:设计状态;
状态
(
i
,
j
)
(i, j)
(i,j) 表示前
i
i
i 个盒子购买的价钱恰好为
j
j
j
(
i
∈
[
0
,
n
]
,
j
∈
[
0
,
m
]
)
(i \in [0, n], j \in [0, m])
(i∈[0,n],j∈[0,m]);
令
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示状态
(
i
,
j
)
(i, j)
(i,j) 下得到的最大价值,即前
i
i
i 个盒子购买价钱为
j
j
j 的情况下所得到的最大总价值;
我们在设计状态的时候,没有把小礼物设计到状态里,那么如何进行状态转移呢?
可以这么考虑,抛开小礼物不说,每个盒子其实只有两种状态,选 和 不选;
1)选:就是要对这个盒子里的小礼物进行一次 0/1 背包;
2)不选:就和这盒子里的小礼物无关了,直接等于前
i
−
1
i-1
i−1 个盒子的最大价值,即
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j]。
那么,只要从前往后枚举所有盒子,
p
[
i
]
p[i]
p[i] 为第
i
i
i 个盒子的价钱,
w
[
i
]
w[i]
w[i] 为价值,由于这个问题下盒子是没有价值的,即
w
[
i
]
w[i]
w[i] 恒等于零;
进行如下三步操作:
1)首先,买第 i i i 个盒子,并且不放物品;
2)然后,既然盒子都已经买下来了,就可以放心对第 i i i 个盒子里的小礼物进行 0/1 背包了;
3)最后,对 买盒子 i i i 和 不买盒子 i i i 取一次最大价值;
买第
i
i
i 个盒子,不放物品的情况肯定是从前
i
−
1
i-1
i−1 个盒子的状态推算过来的,给出状态转移方程如下:
d
p
[
i
]
[
j
]
=
{
i
n
f
j
<
p
[
i
]
(
1
)
d
p
[
i
−
1
]
[
j
−
p
[
i
]
]
+
w
[
i
]
j
≥
p
[
i
]
(
2
)
dp[i][j] =\begin{cases}inf & j < p[i] & (1)\\dp[i-1][j - p[i]]+w[i] & j \ge p[i] & (2)\end{cases}
dp[i][j]={infdp[i−1][j−p[i]]+w[i]j<p[i]j≥p[i](1)(2)
- (1) 代表钱不够,无限凄凉;(2) 代表从 前 i − 1 i-1 i−1 个盒子价格为 j − p [ i ] j - p[i] j−p[i] 时,再花 p [ i ] p[i] p[i] 买下第 i i i 个盒子的情况。这时候 d p [ i ] [ j ] dp[i][j] dp[i][j] 代表的是 第 i i i 个盒子买下后,还没买小礼物时,容量为 j j j 的最大总价值;
既然盒子都已经买下来了,就可以放心对第 i i i 个盒子里的小礼物在 d p [ i ] [ 0... m ] dp[i][0...m] dp[i][0...m] 上进行 0/1 背包了;所有小礼物都枚举完毕以后,得到的 d p [ i ] [ j ] dp[i][j] dp[i][j] 代表的是 第 i i i 个盒子买下,并且买了若干小礼物后,容量为 j j j 的最大总价值;
最后,对买 这个盒子 和 不买这个盒子 做一次选择,即取一次最大价值,如下:
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
]
[
j
]
,
d
p
[
i
−
1
]
[
j
]
)
dp[i][j] = max(dp[i][j], dp[i-1][j])
dp[i][j]=max(dp[i][j],dp[i−1][j])
这里的
d
p
[
i
−
1
]
[
j
]
dp[i-1][j]
dp[i−1][j] 正代表的是第
i
i
i 个盒子不买的情况。
有关依赖背包的更多内容,可以参考:夜深人静写算法(十八)- 依赖背包。
六、树形DP
给定一棵 n ( n < = 150 ) n(n <= 150) n(n<=150) 个结点的树,去掉一些边,使得正好出现一个 P P P 个结点的连通块。问去掉最少多少条边能够达到这个要求。
如图所示,一棵 10 个结点的树,我们可以去掉图中红色的边,变成两棵子树,分别为 3 个结点和 7个结点。
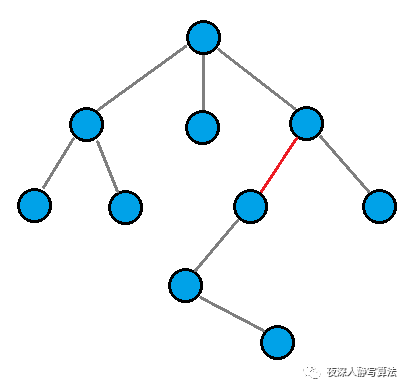
也可以通过这样的方式,得到三颗子树,分别为 5 、4、1 个结点。

对于树上的某个结点(如图的红色结点),可以选择去掉连接子树的边,也可以选择留着;每条连接子树的边的 选 和 不选,能够得到一个组合,对应了背包问题,而每棵子树的选择只能选择一种,对应了分组背包,所以可以利用这个思路来设计状态。
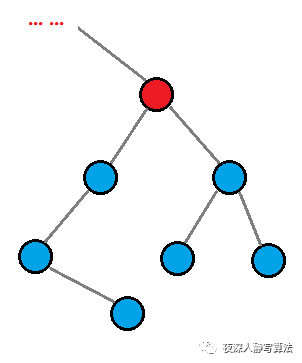
状态设计:用
d
p
[
u
]
[
x
]
dp[u][x]
dp[u][x] 表示以
u
u
u 为根的子树,能够通过去掉一些边而得到一个正好是
x
x
x 结点的连通块(注意只包含它的子树的部分,不连接它的父结点)的最少消耗;
状态转移思路:枚举
u
u
u 的所有子结点,对于子结点
v
v
v,递归计算
d
p
[
v
]
[
i
]
(
1
<
=
i
<
=
x
)
dp[v][i] (1 <= i <= x)
dp[v][i](1<=i<=x) 所有的可能情况,如果
d
p
[
v
]
[
i
]
dp[v][i]
dp[v][i] 存在,则认为这是一个容量为
i
i
i,价值为
d
p
[
v
]
[
i
]
dp[v][i]
dp[v][i] 的物品,表示为
(
i
,
d
p
[
v
]
[
i
]
)
(i, dp[v][i])
(i,dp[v][i])。然后在结点
u
u
u 的背包上进行一次分组背包。
初始情况:对于任何一个结点
u
u
u,它的子结点个数为
c
u
c_u
cu,初始情况是
d
p
[
u
]
[
1
]
=
c
u
dp[u][1] = c_u
dp[u][1]=cu,表示如果以当前这个结点为孤立点,那么它的子树都不能选,所以费用就是去掉所有连接子树的边,即子树的个数。
状态转移:然后对于每棵子树
v
v
v 的
k
k
k 个结点的连通块,答案就是
d
p
[
v
]
[
j
−
k
]
+
d
p
[
v
]
[
k
]
−
1
dp[v][j-k] + dp[v][k] - 1
dp[v][j−k]+dp[v][k]−1,注意这里的 -1 的含义,因为我们一开始默认将所有连接子树的边去掉,所以这里需要补回来。
答案处理:最后的答案就是
min
(
d
p
[
x
]
[
P
]
+
(
1
i
f
x
i
s
n
o
t
r
o
o
t
)
\min(dp[x][P] + (1 \ if \ x \ is \ not \ root)
min(dp[x][P]+(1 if x is not root);考虑结点为 P 的连通块只会出现在两个地方:1)和根结点相连的块,那么答案就是
d
p
[
r
o
o
t
]
[
P
]
dp[root][P]
dp[root][P];2)不和根结点相连的块,需要枚举所有结点的
d
p
[
x
]
[
P
]
+
1
dp[x][P] +1
dp[x][P]+1 取最小值,其中这里的 1 代表斩断
(
p
a
r
e
n
t
[
x
]
,
x
)
(parent[x], x)
(parent[x],x) 这条边的消耗;
七、矩阵二分
A
n
=
[
a
11
a
12
⋯
a
1
m
a
21
a
22
⋯
a
2
m
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
m
]
n
A^n=\begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1m}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2m}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mm}}\\ \end{bmatrix}^n
An=⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1ma2m⋮amm⎦⎥⎥⎥⎤n
对于求矩阵的
n
n
n 次幂,如果采用简单的连乘来求解,这个时间复杂度是完全无法接受的,我们联想到之前提到的整数的二分快速幂(夜深人静写算法(三十)- 二分快速幂),对于矩阵也是同样适用的;
A
n
=
{
I
n
=
0
(
A
n
−
1
2
)
2
×
A
n
为
奇
数
(
A
n
2
)
2
n
为
非
零
偶
数
A^{n} = \begin{cases} I & n = 0\\ (A^{\frac{n-1}{2}})^2 \times A& n 为奇数\\ (A^{\frac{n}{2}})^2 & n 为非零偶数 \end{cases}
An=⎩⎪⎨⎪⎧I(A2n−1)2×A(A2n)2n=0n为奇数n为非零偶数
再加上模加、模乘的性质,矩阵同样满足模幂运算,即:
A
n
m
o
d
M
=
{
I
m
o
d
M
n
=
0
(
A
n
−
1
2
)
2
×
A
m
o
d
M
n
为
奇
数
(
A
n
2
)
2
m
o
d
M
n
为
非
零
偶
数
A^{n} \mod M = \begin{cases} I \mod M & n = 0\\ (A^{\frac{n-1}{2}})^2 \times A \mod M & n 为奇数\\ (A^{\frac{n}{2}})^2 \mod M & n 为非零偶数 \end{cases}
AnmodM=⎩⎪⎨⎪⎧ImodM(A2n−1)2×AmodM(A2n)2modMn=0n为奇数n为非零偶数
如此一来,对于
m
m
m 阶方阵
A
A
A,时间复杂度就可以降到
O
(
m
3
l
o
g
n
)
O(m^3log_n)
O(m3logn);
还是回到本文开头的那个问题,如何计算斐波那契数列第
n
n
n 项模上
M
M
M ?相信聪明的读者已经想到了,我们的主角是:矩阵 !
我们首先来看递推公式:
f
(
n
)
=
f
(
n
−
1
)
+
f
(
n
−
2
)
f(n) = f(n-1) + f(n-2)
f(n)=f(n−1)+f(n−2) 然后我们联想到:1 个
2
×
2
2 \times 2
2×2 的矩阵和 1 个
2
×
1
2 \times 1
2×1 的矩阵相乘,得到的还是一个
2
×
1
2 \times 1
2×1 的矩阵;
首先,利用递推公式填充 列向量 和 矩阵 :
[
f
(
n
)
?
]
=
[
1
1
?
?
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \\ ? \end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]
[f(n)?]=[1?1?][f(n−1)f(n−2)] 接下来利用列向量的传递性把带有问号的列向量补全,得到:
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
?
?
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]
[f(n)f(n−1)]=[1?1?][f(n−1)f(n−2)] 再把带有问号的系数矩阵补全,得到:
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
\left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]
[f(n)f(n−1)]=[1110][f(n−1)f(n−2)] 然后进行逐步化简,得到:
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
[
f
(
n
−
1
)
f
(
n
−
2
)
]
=
[
1
1
1
0
]
[
1
1
1
0
]
[
f
(
n
−
2
)
f
(
n
−
3
)
]
=
[
1
1
1
0
]
⋯
[
1
1
1
0
]
⏟
n
−
1
[
f
(
1
)
f
(
0
)
]
\begin{aligned} \left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] &= \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right] \\ &= \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-2) \\ f(n-3)\end{matrix} \right] \\ &=\underbrace{ \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] {\cdots}\left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] }_{n-1} \left[ \begin{matrix} f(1) \\ f(0)\end{matrix} \right] \\ \end{aligned}
[f(n)f(n−1)]=[1110][f(n−1)f(n−2)]=[1110][1110][f(n−2)f(n−3)]=n−1
[1110]⋯[1110][f(1)f(0)] 最后,根据矩阵乘法结合律,把前面的矩阵合并,得到:
[
f
(
n
)
f
(
n
−
1
)
]
=
[
1
1
1
0
]
n
−
1
[
f
(
1
)
f
(
0
)
]
=
A
n
−
1
[
1
0
]
\begin{aligned} \left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] &=\left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right]^{n-1}\left[ \begin{matrix} f(1) \\ f(0)\end{matrix} \right] \\ &=A^{n-1}\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] \end{aligned}
[f(n)f(n−1)]=[1110]n−1[f(1)f(0)]=An−1[10] 于是,只要利用矩阵二分快速幂求得
A
n
−
1
m
o
d
M
A^{n-1} \mod M
An−1modM ,再乘上初始列向量
[
1
0
]
\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]
[10],得到的列向量的第一个元素就是问题的解了;
事实上,只要列出状态转移方程,当
n
n
n 很大时,我们就可以利用矩阵二分快速幂进行递推式的求解了。
有关矩阵二分的更加深入的内容,可以参考:夜深人静写算法(二十)- 矩阵快速幂。
八、区间DP
有 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 堆石子摆放成一排,第 i i i 堆的重量为 w i w_i wi,现要将石子有次序地合并成一堆。规定每次只能选相邻的二堆合并成新的一堆,合并的消耗为当前合并石子的总重量。试设计出一个算法,计算出将 n n n 堆石子合并成一堆的最小消耗。
在思考用动态规划求解的时候,我们可以先想想如果穷举所有方案,会是什么情况。
对于这个问题来说,我们第一个决策可以选择一对相邻石子进行合并,总共有
n
−
1
n-1
n−1 种情况;对于 5堆 石子的情况,第 1 次合并总共有 4 种选择:
- 1)选择 第 1 堆 和 第 2 堆 的石子进行合并,如图所示:

- 2)选择 第 2 堆 和 第 3 堆 的石子进行合并,如图所示:

- 3)选择 第 3 堆 和 第 4 堆 的石子进行合并,如图所示:

- 4)选择 第 4 堆 和 第 5 堆 的石子进行合并,如图所示:

以上任意一种情况都会把石子变成 4 堆,然后就变成了求解 4 4 4 堆石子的问题;我们可以采用同样方法,把石子变成 3 3 3 堆, 2 2 2 堆,最后变成 1 1 1 堆,从而求出问题的最终解。
当然,这是一个递归的过程,每次合并可以将石子堆数减一,总共进行 n − 1 n-1 n−1 次合并,每个阶段可行的方案数都是乘法的关系,穷举的方案总数就是 ( n − 1 ) ! (n-1)! (n−1)!;
例如,上面提到的剩下的这 4 堆石子,采用深度优先搜索枚举所有可行解的搜索树如图所示:

图中用 ‘-’ 表示不同堆石子之间的分隔符,即 1-2-3-4 代表 4 堆的情况,12-3-4表示 第 1 堆 和第 2 堆 合并后的情况。对这么多种方案取总消耗最小的,正确性是一定可以保证的,因为我们枚举了所有情况,然而时间上肯定是无法接受的。
那么,如何来优化搜索呢?我们发现这个问题的难点在于:当选出的两堆石子合并以后,它的重量变成了合并后的和,对于 n n n 堆石子,选择的 n − 1 n-1 n−1 种合并方式,到达的都是不同的状态,无法进行状态存储。
当没有头绪的时候,我们试着将问题反过来思考;我们发现这棵深度优先搜索树的所有叶子结点都是一样的,这就为我们解决问题带来了突破口;对于 [ 1 , n ] [1, n] [1,n] 堆石子,假设已经合并了 n − 2 n-2 n−2 次,必然只剩下 二堆石子,那么我们只需要合并最后一次,就可以把两堆石子变成一堆,假设合并最后一次的位置发生在 k k k,也就是最后剩下两堆分别为: [ 1 , k ] [1, k] [1,k] 和 [ k + 1 , n ] [k+1, n] [k+1,n],如图二-2-1所示: 注意,这个时候
[
1
,
k
]
[1, k]
[1,k] 和
[
k
+
1
,
n
]
[k+1, n]
[k+1,n] 已经各自合并成一堆了,所以我们把问题转换成了求
[
1
,
k
]
[1, k]
[1,k] 合并一堆的最小消耗,以及
[
k
+
1
,
n
]
[k+1, n]
[k+1,n] 合并成一堆的最小消耗;而这里
k
k
k 的取值范围为
[
1
,
n
−
1
]
[1, n-1]
[1,n−1];
注意,这个时候
[
1
,
k
]
[1, k]
[1,k] 和
[
k
+
1
,
n
]
[k+1, n]
[k+1,n] 已经各自合并成一堆了,所以我们把问题转换成了求
[
1
,
k
]
[1, k]
[1,k] 合并一堆的最小消耗,以及
[
k
+
1
,
n
]
[k+1, n]
[k+1,n] 合并成一堆的最小消耗;而这里
k
k
k 的取值范围为
[
1
,
n
−
1
]
[1, n-1]
[1,n−1];
利用这样的方法,逐步将区间缩小成 1,就可以得到整个问题的解了。令 f [ i ] [ j ] f[i][j] f[i][j] 表示从 第 i i i 堆 石子到 第 j j j 堆 石子合并成一堆所花费的最小代价。 f [ i ] [ j ] = { 0 i = j min k = i j − 1 ( f [ i ] [ k ] + f [ k + 1 ] [ j ] + c o s t ( i , j ) ) i ≠ j f[i][j] = \begin{cases} 0 & i=j\\ \min_{k=i}^{j-1}(f[i][k] + f[k+1][j] + cost(i,j)) & i \neq j\end{cases} f[i][j]={0mink=ij−1(f[i][k]+f[k+1][j]+cost(i,j))i=ji=j
其中 c o s t ( i , j ) = ∑ k = i j w k cost(i, j) = \sum_{k=i}^{j}w_k cost(i,j)=∑k=ijwk
有了上面 “正难则反” 的解释,这个状态转移方程就很好理解了;
1)当 i = j i=j i=j 时,由于 f [ i ] [ j ] f[i][j] f[i][j] 已经是一堆了,所以消耗自然就是 0 了;
2)当 i ≠ j i \neq j i=j 时,我们需要把目前剩下的两堆合并成一堆,一堆是 f [ i ] [ k ] f[i][k] f[i][k] ,另一堆是 f [ k + 1 ] [ j ] f[k+1][j] f[k+1][j],这两堆合并的消耗就是 从 第 i i i 堆到第 j j j 堆的重量之和,即 c o s t ( i , j ) = ∑ k = i j w k cost(i, j) = \sum_{k=i}^{j}w_k cost(i,j)=∑k=ijwk,而对于合并方案,总共 k = j − i k=j-i k=j−i 种选择,所以枚举 j − i j-i j−i 次,取其中最小值就是答案了。
通过记忆化搜索求解 f [ 1 ] [ n ] f[1][n] f[1][n] 就是最后的答案。
如图所示的动图,展示的是迭代求解的顺序,灰色的格子代表无效状态,红色的格子代表为长度为 2 的区间,橙色的格子代表为长度为 3 的区间,金黄色的格子则代表长度为 4 的区间,黄色的格子代表我们最终要求的区间状态,即 f [ 1 ] [ 5 ] f[1][5] f[1][5]。

有关区间DP的更深入内容,可以参考:夜深人静写算法(二十七)- 区间DP。
九、数位DP
如果一个数的所有位数加起来是 10 10 10 的倍数, 则称之为 g o o d n u m b e r good \ number good number,求区间 [ l , r ] ( 0 ≤ l ≤ r ≤ 1 0 18 ) [l, r](0 \le l \le r \le 10^{18}) [l,r](0≤l≤r≤1018) 内 g o o d n u m b e r good \ number good number 的个数;
对于这个问题,朴素算法就是枚举区间里的每个数,并且判断可行性,时间复杂度为
o
(
(
r
−
l
)
c
)
o((r-l)c)
o((r−l)c),
c
=
19
c=19
c=19,肯定是无法接受的。
对于区间
[
l
,
r
]
[l, r]
[l,r] 内求满足数量的数,可以利用差分法分解问题;
假设
[
0
,
x
]
[0, x]
[0,x] 内的
g
o
o
d
n
u
m
b
e
r
good \ number
good number 数量为
g
x
g_x
gx,那么区间
[
l
,
r
]
[l, r]
[l,r] 内的数量就是
g
r
−
g
l
−
1
g_r - g_{l-1}
gr−gl−1;分别用同样的方法求出
g
r
g_r
gr 和
g
l
−
1
g_{l-1}
gl−1,再相减即可;
如果一个数字
i
i
i 满足
i
<
x
i < x
i<x,那么
i
i
i 从高到低肯定出现某一位,使得这一位上的数值小于
x
x
x 对应位上的数值,并且之前的所有高位都和
x
x
x 上的位相等。
举个例子,当
x
=
1314
x = 1314
x=1314 时,
i
=
0
a
b
c
i=0abc
i=0abc、
i
=
12
a
b
i=12ab
i=12ab、
i
=
130
a
i=130a
i=130a、
i
=
1312
i=1312
i=1312,那么对于
i
i
i 而言,无论后面的字母取什么数字,都是满足
i
<
x
i < x
i<x 这个条件的。

如果我们要求
g
1314
g_{1314}
g1314 的值,可以通过枚举高位:当最高位为0,那么问题就转化成
g
999
g_{999}
g999 的子问题;当最高位为1,问题就转化成
g
314
g_{314}
g314 的子问题。
g
314
g_{314}
g314 可以继续递归求解,而
g
999
g_{999}
g999 由于每一位数字范围都是
[
0
,
9
]
[0,9]
[0,9],可以转换成一般的动态规划问题来求解。
这里的前缀状态就对应了之前提到的 某些条件;
在这个问题中,前缀状态的描述为:一个数字前缀的各位数字之和对10取余(模)的值。前缀状态的变化过程如图所示:

在上题中,前缀状态的含义是:对于一个数 520 ,我们不需要记录 520 ,而只需要记录 7;对于 52013,我们不需要记录 52013,而只需要记录 1。这样就把原本海量的状态,变成了最多 10 个状态。
根据以上的三个信息,我们可以从高位到低位枚举数字
i
i
i 的每一位,逐步把问题转化成小问题求解。
我们可以定义
f
(
n
,
s
t
,
l
i
m
)
f(n, st, lim)
f(n,st,lim) 表示剩下还需要考虑
n
n
n 位数字,前面已经枚举的高位组成的前缀状态为
s
t
st
st,且用
l
i
m
lim
lim 表示当前第
n
n
n 位是否能够取到最大值(对于
b
b
b 进制,最大值就是
b
−
1
b-1
b−1,比如 10 进制状态下,最大值就是 9) 时的数字个数。我们来仔细解释一下这三维代表的含义:
- 1)当前枚举的位是 n n n 位, n n n 大的代表高位,小的代表低位;
- 2)
s
t
st
st 就是前缀状态,在这个问题中,代表了所有已经枚举的高位(即数字前缀)的各位数字之和对10取余(模)。注意:我们并不关心前缀的每一位数字是什么,而只关心它们加和模10之后的值是什么。

- 3)
l
i
m
=
t
r
u
e
lim=true
lim=true 表示的是已经枚举的高位中已经出现了某一位比给定
x
x
x 对应位小的数,那么后面枚举的每个数最大值就不再受
x
x
x 控制;否则,最大值就应该是
x
x
x 的对应位。举例说明,当十进制下的数
x
=
1314
x = 1314
x=1314 时,枚举到高位前三位为 “131”,
l
i
m
=
f
a
l
s
e
lim = false
lim=false, 那么第四位数字的区间取值就是
[
0
,
4
]
[0,4]
[0,4];而枚举到高位前三位为 “130” 时,
l
i
m
=
t
r
u
e
lim = true
lim=true,那么第四位数字的区间取值就是
[
0
,
9
]
[0, 9]
[0,9]。
所以,我们根据以上的状态,预处理 x x x 的每个数位,表示成十进制如下: x = d n d n − 1 . . . d 1 x = d_nd_{n-1}...d_1 x=dndn−1...d1 (其中 d n d_n dn 代表最高位, d 1 d_1 d1 代表最低位)
得出状态转移方程如下: f ( n , s t , l i m ) = ∑ k = 0 m a x v f ( n − 1 , ( s t + k ) m o d 10 , l i m o r ( k < m a x v ) ) \begin{aligned}& f(n, st, lim) \\ &= \sum_{k=0}^{maxv} f(n-1, (st+k) \mod 10, lim \ or \ (k < maxv))\end{aligned} f(n,st,lim)=k=0∑maxvf(n−1,(st+k)mod10,lim or (k<maxv))
k k k 表示第 n n n 位取什么数字,它的范围是 [ 0 , m a x v ] [0, maxv] [0,maxv];
m a x v maxv maxv 表示第 n n n 位能够取到的最大值,它由 l i m lim lim 决定,即:
m a x v = { 9 l i m = t r u e d n l i m = f a l s e maxv = \begin{cases}9 & lim = true\\d_n & lim = false\end{cases} maxv={9dnlim=truelim=false
利用上述的状态转移方程,我们可以进行递归求解,并且当 n = 0 n=0 n=0 的时候为递归出口,由于数字要求满足所有数字位数之和为 10 10 10 的倍数,所以只有 s t = 0 st = 0 st=0 的情况为合法状态,换言之,当 n = 0 n=0 n=0 时,有: f ( 0 , x , l i m ) = { 1 x = 0 0 0 < x ≤ 9 f(0, x, lim) = \begin{cases} 1 & x = 0\\ 0 & 0 \lt x \le 9\end{cases} f(0,x,lim)={10x=00<x≤9 而我们需要求的,就是 f ( n , 0 , f a l s e ) f(n, 0, false) f(n,0,false)。
我们发现,如果按照以上的状态转移进行求解,会导致一个问题,就是会有很多重叠子问题,所以需要进行记忆化,比较简单的方法就是用一个三维数组 f [ n ] [ s t ] [ l i m ] f[n][st][lim] f[n][st][lim] 来记忆化。
当然,这里有一个技巧,就是 l i m lim lim 这个变量只有 t r u e true true、 f a l s e false false 两种取值,并且当它为 f a l s e false false 时,代表之前枚举的数的高位和所求区间 [ 0 , x ] [0, x] [0,x] 右端点中的 x x x 的高位保持完全一致,所以当 l i m = f a l s e lim = false lim=false 时,深度优先搜索树的分支最多只有 1 1 1 条,所以无须记忆化,每次直接算就可以。如图二-3-2所示的蓝色结点,就是那条唯一分支。
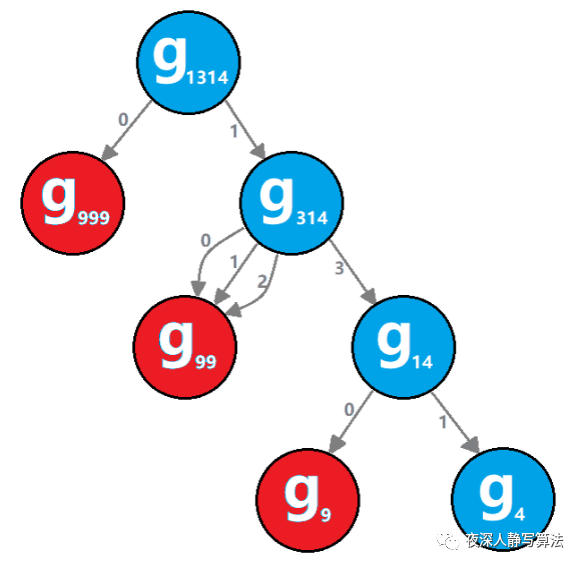
综上所述,我们只需要用 f [ n ] [ s t ] f[n][st] f[n][st] 表示长度为 n n n,且每个数字的范围为 [ 0 , m a x v ] [0, maxv] [0,maxv],且前缀状态为 s t st st 的数字个数(这里 m a x v maxv maxv 和进制有关,如果是 b b b 进制,那么 m a x v = b − 1 maxv = b - 1 maxv=b−1)。 -
f
(
n
,
s
t
,
f
a
l
s
e
)
f(n, st, false)
f(n,st,false) 采用普通深搜,
f
(
n
,
s
t
,
t
r
u
e
)
f(n, st, true)
f(n,st,true) 采用记忆化搜索。
对于更加深入的数位DP的实现,可以参考:夜深人静写算法(二十九)- 数位DP。
十、状态压缩DP
给出 g r a p h graph graph 为有 n ( n ≤ 12 ) n(n \le 12) n(n≤12) 个节点(编号为 0, 1, 2, …, n − 1 n-1 n−1)的无向连通图。 g r a p h . l e n g t h = n graph.length = n graph.length=n,且只有节点 i i i 和 j j j 连通时, j j j 不等于 i i i 时且在列表 g r a p h [ i ] graph[i] graph[i] 中恰好出现一次。返回能够访问所有节点的最短路径的长度。可以在任一节点 开始 和 结束,也可以多次重访节点,并且可以重用边。
这是一个可重复访问的 旅行商问题。我们可以设计状态如下:
f
(
s
t
,
e
n
,
s
t
a
t
e
)
f(st, en, state)
f(st,en,state) 代表从
s
t
st
st 到
e
n
en
en,且 经过的节点 的状态组合为
s
t
a
t
e
state
state 的最短路径。
状态组合的含义是:经过二进制来压缩得到的一个数字,比如 经过的节点 为 0、1、4,则
s
t
a
t
e
state
state 的二进制表示为:
(
10011
)
2
(10011)_2
(10011)2 即 经过的节点 对应到状态
s
t
a
t
e
state
state 二进制表示的位为 1,其余位为 0。
于是,我们明确以下几个定义:初始状态、最终状态、非法状态、中间状态。
初始状态
初始状态 一定是我们确定了某个起点,想象一下,假设起点在
i
i
i,那么在一开始的时候,必然
s
t
a
t
e
=
2
i
state = 2^i
state=2i。于是,我们可以认为起点在
i
i
i,终点在
i
i
i,状态为
2
i
2^i
2i 的最短路径为 0。也就是初始状态表示如下:
f
(
i
,
i
,
2
i
)
=
0
i
∈
[
0
,
n
)
f(i, i, 2^i) = 0 \\ \ \\ i \in [0, n)
f(i,i,2i)=0 i∈[0,n)
最终状态
由于这个问题,没有告诉我们 起点 和 终点,所以 起点 和 终点 是不确定的,我们需要通过枚举来得出,所以最终状态 起点
i
i
i 和 终点
j
j
j,状态为
2
n
−
1
2^n-1
2n−1(代表所有点都经过,二进制的每一位都为 1)。最终状态表示为:
f
(
i
,
j
,
2
n
−
1
)
i
∈
[
0
,
n
)
,
j
∈
[
0
,
n
)
f(i, j, 2^n-1) \\ \ \\ i \in [0, n), j \in [0, n)
f(i,j,2n−1) i∈[0,n),j∈[0,n)
非法状态
非法状态 就是 不可能从初始状态 通过 状态转移 到达的状态。我们设想一下,如果
f
(
i
,
j
,
s
t
a
t
e
)
f(i, j, state)
f(i,j,state) 中
s
t
a
t
e
state
state 的二进制的第
i
i
i 位为 0,或者第
j
j
j 位 为 0,则这个状态必然是非法的,它代表了两个矛盾的对立面。
我们把非法状态下的最短路径定义成
i
n
f
=
10000000
inf = 10000000
inf=10000000 即可。
f
(
i
,
j
,
s
t
a
t
e
)
=
i
n
f
f(i, j, state) = inf
f(i,j,state)=inf
其中 (state & (1<<i)) == 0或者(state & (1<<j)) == 0代表state的二进制表示的第
i
i
i 和
j
j
j 位没有 1。
中间状态
除了以上三种状态以外的状态,都成为中间状态。
那么,我们可以通过 记忆化搜索,枚举所有的 f ( i , j , 2 n − 1 ) f(i, j, 2^n - 1) f(i,j,2n−1) 的,求出一个最小值就是我们的答案了。状态数: O ( n 2 2 n ) O(n^22^n) O(n22n),状态转移: O ( n ) O(n) O(n),时间复杂度: O ( n 3 2 n ) O(n^32^n) O(n32n)。
十一、斜率DP
给定 n ( n ≤ 400000 ) n(n \le 400000) n(n≤400000) 个数 a n a_n an,现在需要将它们归类,每类至少 t ( 1 < t ≤ n ) t(1 < t \le n) t(1<t≤n) 个数。归在同一类的花费为每个数字减去最小那个数字之和。希望所有数归类后的总花费最小,求这个最小花费。
首先贪心,排个序先。然后用
s
u
m
[
i
]
sum[i]
sum[i] 代表前
i
i
i 个数的和,其中
s
u
m
[
0
]
=
0
sum[0]=0
sum[0]=0,
d
p
[
i
]
dp[i]
dp[i] 代表前
i
i
i 个数字归完类后的最小花费,则容易列出状态转移方程:
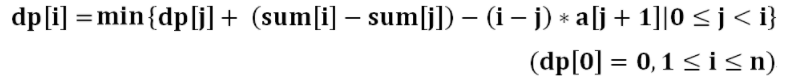
因为是排好序的,所以
a
[
j
+
1
]
a[j+1]
a[j+1] 是
a
[
j
+
1
:
i
]
a[j+1:i]
a[j+1:i] 这个区间内最小的那个数,这是个
1
D
/
1
D
1D/1D
1D/1D 问题,即状态数为
O
(
n
)
O(n)
O(n),每个状态的转移成本为
O
(
n
)
O(n)
O(n),所以总的算法复杂度为
O
(
n
2
)
O(n^2)
O(n2)。朴素算法如下:

由于
n
n
n 的范围太大,需要优化。算法优化的本质就是让上述代码的第一层循环不变,减少第二层循环的状态转移过程。首先将状态转移方程进行移项,得到如下等式:
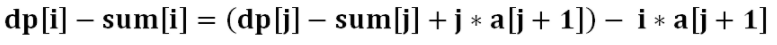
看上去貌似并没有什么变化,这么做的目的是什么呢?再来仔细看下这个式子:

这样一看,基本上就能看懂分类依据了,红色代表自变量为i的函数,绿色代表自变量为j的函数,蓝色则是以
i
i
i 和
j
j
j 为变量的函数,那么我们做进一步转化,使得该公式更加清晰。

将
i
i
i 和
j
j
j 为自变量的函数分别用b和y表示,
k
=
i
k=i
k=i 代表斜率。于是,状态转移方程转化成了以
a
[
j
+
1
]
a[j+1]
a[j+1] 为自变量,
i
i
i 为斜率,
d
p
[
i
]
−
s
u
m
[
i
]
dp[i]-sum[i]
dp[i]−sum[i] 为截距的直线方程。

如上图所示,当
i
i
i 确定,
j
j
j 取
t
t
t 时,则代表的是一条斜率为
i
i
i,并且过点
T
(
a
[
t
+
1
]
,
d
p
[
t
]
−
s
u
m
[
t
]
+
t
∗
a
[
t
+
1
]
)
T(a[t+1], dp[t]-sum[t]+t*a[t+1])
T(a[t+1],dp[t]−sum[t]+t∗a[t+1]) 的直线。

更加一般地,当
i
i
i 确定,
j
j
j 取不同值时,则这个平面上会出现一系列平行的直线,他们的斜率都是
i
i
i。因为
i
i
i 是确定的,并且所有直线的斜率就是
i
i
i,所以所有直线相互平行;又由于
j
j
j 的不同,直线经过不同的点,所以只要是两条不重合的平行直线,截距必然不同,而截距
b
=
d
p
[
i
]
−
s
u
m
[
i
]
b=dp[i]-sum[i]
b=dp[i]−sum[i],即
d
p
[
i
]
=
b
+
s
u
m
[
i
]
dp[i]=b+sum[i]
dp[i]=b+sum[i];所以可以得出结论:
dp[i]的最小值一定出现在最下面的那条直线上(因为最下面的直线截距最小)。
接下来,我们分析几条比较重要的性质:
第一条:维护“下凸”折线

如图所示,A、B、C三个点,其中B点位于AC直线之上,即为一个“上凸”点。然后我们连接AC两点,绘制所有的斜率小于K(A,C)的直线(图中绿色直线),发现截距最小的一定是经过点A的直线(想象一下,图中三根绿色的直线一起动起来的情况);然后绘制所有的斜率大于K(A,C)的直线(图中红色直线),发现截距最小的一定是经过C的直线。于是,可以得出结论,在用A、B、C进行状态转移时,B永远是一个无用的状态转移。
由于任意三点不能出现“上凸”。所以,所有用于状态转移的点必须是一条“下凸”折线,如图所示:
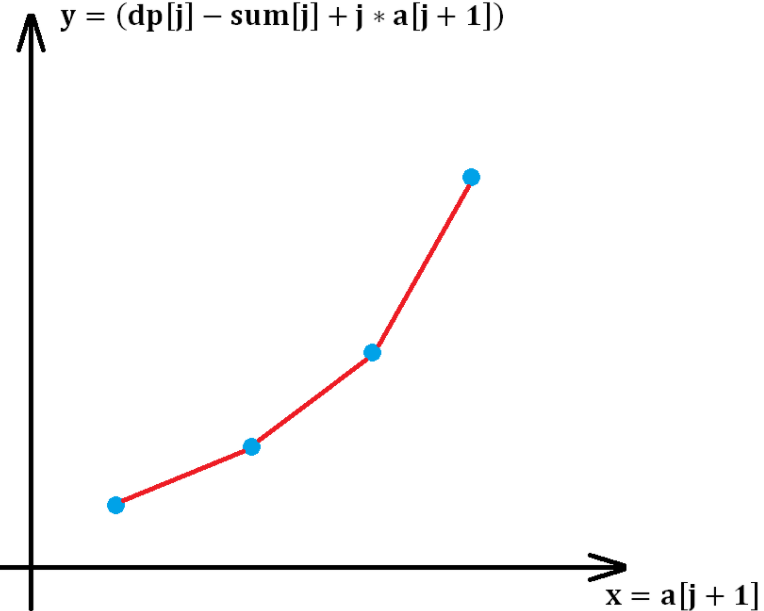
图中每个点都代表了向dp[i]进行状态转移的dp[j]。从图中可以看出,“下凸”折线满足每段折线斜率单调递增。那么如何维护这段“下凸”折线?
我们采用双端队列来维护,由于它存储结构的单调性(斜率单调),又称为“单调队列”。deq[]代表单调队列的数据域,head和tail分别表示它的两个指针,当 head和tail相等则代表单调队列为空,初始化head=tail=0。deq[]中的每个元素存的是原数组的下标,因为通过下标就能计算出坐标图中点的 x-y坐标,也就能计算相邻两点之间的斜率了。
那么每次我们将一个可行的转移状态j放入单调队列之前,先判断它的加入能否保证斜率单调递增,如果不能则将单调队列尾元素删除,依次往复,最后将这个点放入单调队列尾部,这样一条“下凸”折线就算维护完毕了。
细心的读者,会发现这一步操作同样可以用“栈”这种数据结构来完成。接下来,我们继续来探讨为什么用双端队列不用栈。
第二条:“永不录用”点的剔除
“永不录用”这个名字是我自己起的,那么哪些点是“永不录用”点?,还是来看图:
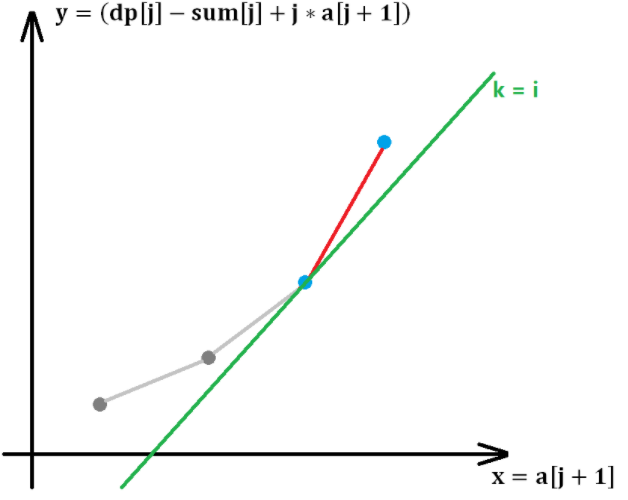
由于每次枚举状态i时是递增的枚举(之前那段代码的第一个for循环),也就是说斜率一定是越来越大,那么从图中可以看出,那些斜率小于i的折线上的点(灰色点)如果要经过斜率为i的直线(图中绿色直线的平行线),则产生的截距必然不会比图中绿色直线的更小,也就是灰色点都可以删除了。
这些可以删除的灰色点就是“永不录用”点。“永不录用”点更加官方的说法,就是单调队列里的折线中,所有斜率小于i的折线的左端点。由于单调队列的斜率单调性,所以删除点的操作可以从左往右进行,这就是为什么之前不用栈来维护的根本原因。如果维护折线用的是栈,则最左边的点势必在栈底,而栈这种数据结构只能获取栈顶元素。
十二、连通性DP
我觉得你应该也看不到这里,如果你看到了这里,那请在评论区说一句:“我看到了!”。那我只能说:草率了。
这应该是 ACM 中最难的动态规划问题了,所以我打算专门拿一篇文章来讲它,放心吧,职场面试一定不会考,如果考到了,那么面试官一定是想秀一下演技。
关于 「 动态规划 」 的内容到这里就结束了。
如果还有不懂的问题,可以通过 「 电脑版主页 」找到作者的「 联系方式 」 ,线上沟通交流。
有关🌳《画解数据结构》🌳 的源码均开源,链接如下:《画解数据结构》

相信看我文章的大多数都是「 大学生 」,能上大学的都是「 精英 」,那么我们自然要「 精益求精 」,如果你还是「 大一 」,那么太好了,你拥有大把时间,当然你可以选择「 刷剧 」,然而,「 学好算法 」,三年后的你自然「 不能同日而语 」。
那么这里,我整理了「 几十个基础算法 」 的分类,点击开启:
如果链接被屏蔽,或者有权限问题,可以私聊作者解决。
大致题集一览:
为了让这件事情变得有趣,以及 「 照顾初学者 」,目前题目只开放最简单的算法 「 枚举系列 」 (包括: 线性枚举、双指针、前缀和、二分枚举、三分枚举),当有 一半成员刷完 「 枚举系列 」 的所有题以后,会开放下个章节,等这套题全部刷完,你还在群里,那么你就会成为 「 夜深人静写算法 」专家团 的一员。
不要小看这个专家团,三年之后,你将会是别人 望尘莫及 的存在。如果要加入,可以联系我,考虑到大家都是学生, 没有「 主要经济来源 」,在你成为神的路上, 「 不会索取任何 」。
🔥让天下没有难学的算法🔥
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习,抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜
粉丝专属福利
语言入门(基础):《光天化日学C语言》示例代码全解析
语言训练(进阶):《C语言入门100例》精装版
数据结构(大学):《画解数据结构》源码
算法入门(职场):《算法入门》指引
算法进阶(竞赛):《夜深人静写算法》算法模板
验证码可在公号取。如果还有上学、竞赛、职场上的问题,以及更多资源的获取,可以 「 私聊 」作者,或者通过「 电脑版主页左侧 」找到作者的的「 联系方式 」 进行交流探讨。
如果你满足如下:
(
1
)
(1)
(1) 有强烈欲望「 想要学好C语言 」的人
(
2
)
(2)
(2) 有强烈欲望「 想要学好C++ 」的人
(
3
)
(3)
(3) 有强烈欲望「 想要学好数据结构 」的人
(
4
)
(4)
(4) 有强烈欲望「 想学好算法 」的人
(
5
)
(5)
(5) 有强烈欲望「 想进大厂 」的人
如果你满足以上任意一点,那么,我们就是志同道合的人啦!
🔥联系作者,或者扫作者主页二维码加群,加入我们吧🔥



