⚡终于!!!
⚡终于又有时间学习Deep Learning了⚡!
30天ML计划,一起加油!!!
https://blog.csdn.net/weixin_44333889/category_11271153.html《专栏》
在训练NN的时候,有哪些Optimizers可以优化更快的找到global Minima?
下面我们来看下有哪些方法可以优化求解。
Background
在训练神经网路的时候,最开始我们是用的Gradient Descent(梯度下降法,GD)来求解,但是会出现很多问题,面临大量的数据的时候,GD会出现local Minima,而且求解速度会下降。
关于GD+Momentum,可以看这个介绍简单易懂。
整个技术的发展路线如下:
- SGD 【Cauchy,1847】
- SGD with momentum 【Rumelhart,et al.,Nature’1986】
上面两个是远古时期的优化求解方法,其实放到现在来看,依旧还是很有效果。
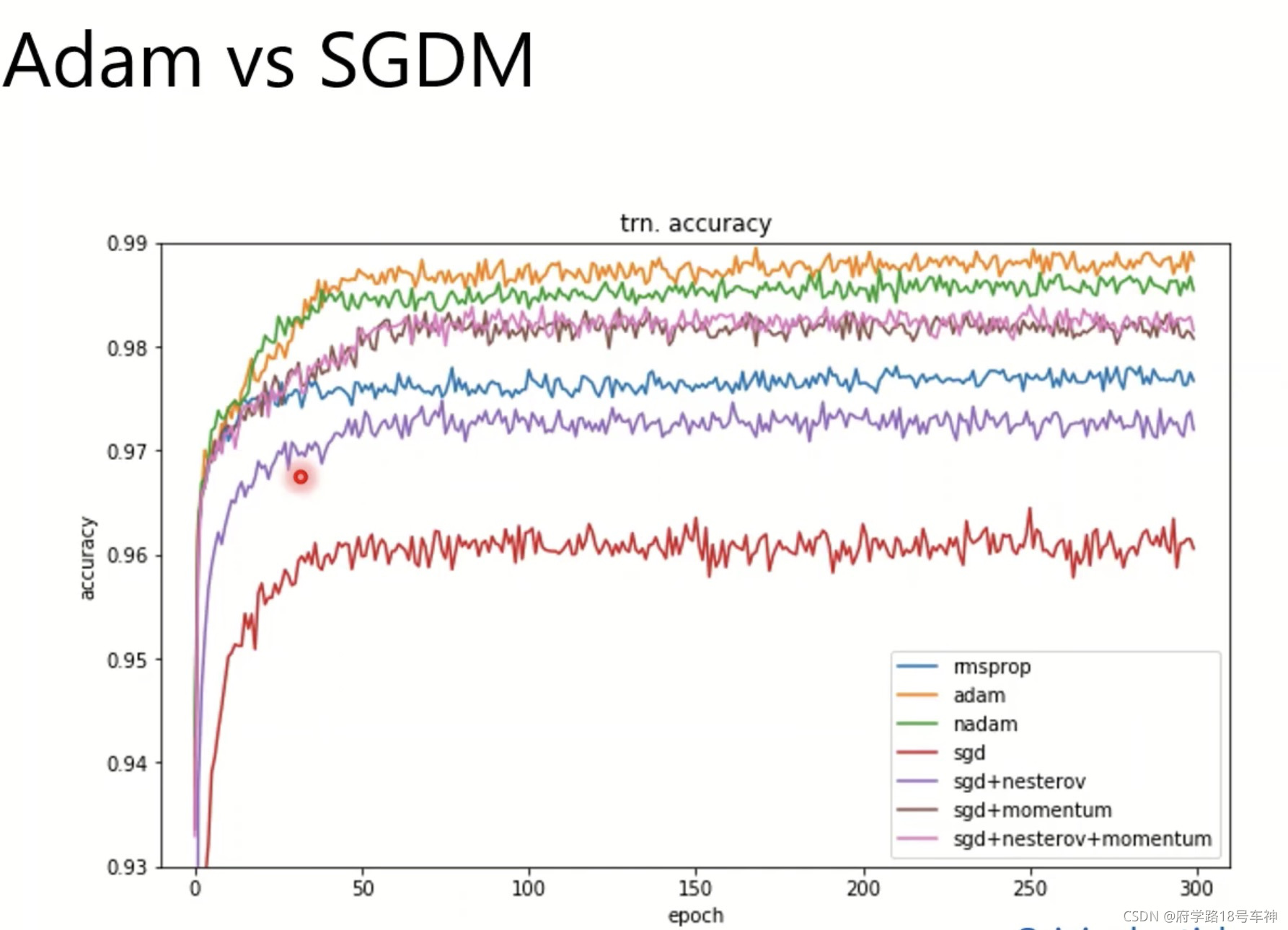
如下面这些就是SGDM训练出来的,

目前比较常用的是下面三个Optimizers:
- Adagrad 【Duchi,et al. JMLR’11 2011】
- RMSProp 【Hinton,et al. Lecture slides, 2013】
- Adam 【kingma,et al. ICLR’15 2014】
借用一下李老师(台大,李宏毅)的PPT。
SGD,stochastic gradient descent。也就是最普通的方法,如下图所示
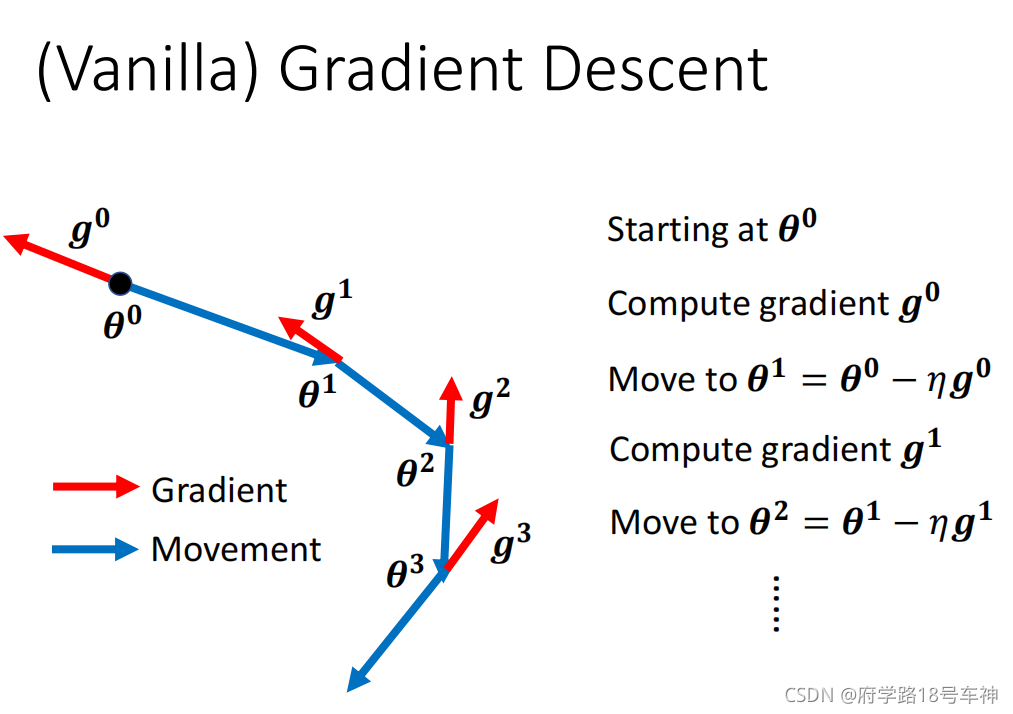
SGD就像图中的更新方式一样,随机找到一个起始点,对其求梯度,然后在其梯度的反方向按照
η
\eta
η步长进行更新,找到下一个点,然后在不断的重复操作,直到找到Minima。
关于SGDM的更新方式如下图。可以看出,更新方式在SGD的基础上,增加了Momentum,而这个Momentum则是在一次梯度下降后,按照其算的梯度方向的反方向(图中 g 1 g^1 g1)和上一个更新方向的延长(图中 m 1 m^1 m1)的合成方向(图中 m 2 m^2 m2)的方向进行更新操作的。不断的进行更新,直到找到最优的解则停止。

Adagrad
Adagrad(自适应梯度算法)。其基本思想是,对每个参数theta自适应的调节它的学习率,自适应的方法就是对每个参数乘以不同的系数,并且这个系数是通过之前累积的梯度大小的平方和决定的,也就是说,对于之前更新很多的,相对就可以慢一点,而对那些没怎么更新过的,就可以给一个大一些的学习率。
Adagrad算法:
- 参数设置: ϵ \epsilon ϵ 为全局学习率;初始参数 θ \theta θ;较小的常数(超参数,自己设定) δ \delta δ,为了数值稳定大约设置为 1 0 − 7 10^{-7} 10−7
- 初始化梯度累积变量 r = 0 r=0 r=0
接下来是循环迭代更新
while 没有达到停止准则 do
- 从训练集中采包含 m m m个样本 { x ( 1 ) , . . . , x ( m ) } \{x^{(1)},...,x^{(m)}\} {x(1),...,x(m)}的小批量,对应目标为 y ( i ) y^{(i)} y(i)
- 计算梯度: g ← 1 m ▽ θ Σ i L ( x ( 1 ) ; θ , y ( i ) ) g \leftarrow \frac{1}{m} \bigtriangledown _\theta\Sigma_i L(x^{(1)};\theta,y^{(i)}) g←m1▽θΣiL(x(1);θ,y(i))
- 累积平方梯度: r ← r + g ⊙ g r\leftarrow r+g \odot g r←r+g⊙g
- 计算更新: △ θ ← − ϵ δ + r ⊙ g \bigtriangleup \theta\leftarrow - \frac{\epsilon}{\delta+\sqrt{r}}\odot g △θ←−δ+r ϵ⊙g(逐步元素地应用除和求平方根)
- 应用更新: θ ← θ + △ θ \theta\leftarrow \theta+\bigtriangleup \theta θ←θ+△θ
end
(结束优化更新)
以上就为Adagrad算法的内容。
Python实现代码:
import numpy as np
class Adagrad:
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate # 学习率设置为0.01
self.fg = None
self.delta = 1e-07 # 设置1e-07微小值避免分母为0
def update(self, params, grads): # 更新操作
if self.fg is None:
self.fg = {} # 设为空列表
for key, value in params.items():
self.fg[key] = np.zeros_like(value) # 构造一个矩阵
for key in params.keys(): # 循环迭代
self.fg[key] += grads[key] * grads[key]
params[key] -= self.learning_rate * grads[key] / (np.sqrt(self.fg[key]) + self.delta)
RMSProp
RMSProp算法实则为对Adagrad的一个改进,也就是把Adagrad对历史梯度加和变成了对历史梯度求均值,再利用这个均值代替Adagrad累加的梯度和对当前梯度进行加权,并用来update更新。
用均值代替求和是为了解决Adagrad的学习率逐渐消失的问题。

(图片源自网络)
有位大佬的解释更加清晰,可跳转此处。
def RMSprop(x, y, step=0.01, iter_count=500, batch_size=4, alpha=0.9, beta=0.9):
length, features = x.shape
data = np.column_stack((x, np.ones((length, 1))))
w = np.zeros((features + 1, 1))
Sdw, v, eta = 0, 0, 10e-7
start, end = 0, batch_size
# 开始迭代
for i in range(iter_count):
# 计算临时更新参数
w_temp = w - step * v
# 计算梯度
dw = np.sum((np.dot(data[start:end], w_temp) - y[start:end]) * data[start:end], axis=0).reshape((features + 1, 1)) / length
# 计算累积梯度平方
Sdw = beta * Sdw + (1 - beta) * np.dot(dw.T, dw)
# 计算速度更新量、
v = alpha * v + (1 - alpha) * dw
# 更新参数
w = w - (step / np.sqrt(eta + Sdw)) * v
start = (start + batch_size) % length
if start > length:
start -= length
end = (end + batch_size) % length
if end > length:
end -= length
return w
Adam
最后讲讲Adam(自适应矩估计 Adaptive moment estimation),因为目前是比较强的,下面这些都是由Adam训练出来的,

看一下Adam和SGDM的准确率对比(源自论文)
由于Adam的提出的地方有一些突兀,并非在论文或会议,能找到的最原始的出处也只有下面了,看一下他的更新方式吧,相当于一个优化参数的更新模块。

简单翻译一下上面的更新步骤:
首先,参数设置: g t 2 = g t ⊙ g t g_t^2=g_t \odot g_t gt2=gt⊙gt,默认测试的学习率(LR) α = 0.001 \alpha=0.001 α=0.001,各种超参数 β 1 = 0.9 、 β 2 = 0.999 、 ϵ = 1 0 − 8 \beta _1=0.9、\beta_2=0.999、\epsilon =10^{-8} β1=0.9、β2=0.999、ϵ=10−8
- α \alpha α: 步长(Stepsize)亦或学习率
- β 1 , β 2 ∈ [ 0 , 1 ] \beta _1,\beta _2\in[0,1] β1,β2∈[0,1]:矩估计的指数衰减率
- f ( θ ) f(\theta) f(θ):参数 θ \theta θ 的随机目标函数值
- θ 0 \theta_0 θ0: 初始参数向量{ m 0 ← 0 m_0 \leftarrow0 m0←0:(初始化第一权值向量)、 v 0 ← 0 v_0\leftarrow0 v0←0:(初始化第二权值向量)、 t ← 0 t\leftarrow0 t←0:(初始化时变步长)}
下面为约束,当且仅当 θ t \theta_t θt 不收敛的时候执行以下操作:
- t ← t + 1 t\leftarrow t+1 t←t+1
- g t ← ▽ θ f t ( θ t − 1 ) g_t \leftarrow \bigtriangledown _{\theta}f_{t}(\theta_{t}-1) gt←▽θft(θt−1) :(获得新一轮更新的梯度值(参数 t t t 是上次刚更新的步长))
- m t ← β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t m_t \leftarrow \beta_1\cdot m_{t-1}+(1-\beta_1)\cdot g_t mt←β1⋅mt−1+(1−β1)⋅gt:(更新带偏差的第一权重估计值)
- v t ← β 2 ⋅ v t − 1 + ( 1 − β 1 t ) ⋅ g t 2 v_t\leftarrow\beta_2 \cdot v_{t-1}+(1-\beta_1^t)\cdot{g_t^2} vt←β2⋅vt−1+(1−β1t)⋅gt2:(更新带偏差的第二原始权重估计值)
- m t ^ ← m t / ( 1 − β 2 t ) \hat {m_t}\leftarrow m_t / (1-\beta_2^t) mt^←mt/(1−β2t):(计算偏差校正后的第一权重估计值)
- v t ^ ← v t / ( 1 − β 2 t ) \hat {v_t}\leftarrow v_t/(1-\beta_2^t) vt^←vt/(1−β2t):(计算偏差校正后的第二原始权重估计值)
- θ t ← θ t − 1 − α ⋅ m t ^ / ( v t ^ + ϵ ) \theta_t\leftarrow \theta_{t-1}-\alpha \cdot \hat{m_t}/(\sqrt{\hat{v_t}}+\epsilon) θt←θt−1−α⋅mt^/(vt^ +ϵ):(更新 θ \theta θ 参数值)
到此参数优化结束。
返回 θ t \theta_t θt 的值。
Adam 的Python代码有大佬已经开源了:
- https://github.com/yzy1996/Python-Code/blob/master/Algorithm/Optimization-Algorithm/Adam.py
- https://github.com/sagarvegad/Adam-optimizer/blob/master/Adam.py
如果不想转链接,这里直接附上了:
import math
alpha = 0.01
beta_1 = 0.9
beta_2 = 0.999 # 初始化参数的值
epsilon = 1e-8
def func(x):
return x*x -4*x + 4
def grad_func(x): # 计算梯度
return 2*x - 4
theta_0 = 0 # 初始化向量
m_t = 0
v_t = 0
t = 0
while (1): # 循环直到它收敛
t+=1
g_t = grad_func(theta_0) # 计算随机函数的梯度
m_t = beta_1*m_t + (1-beta_1)*g_t # 更新梯度的移动平均线
v_t = beta_2*v_t + (1-beta_2)*(g_t*g_t) # 更新平方梯度的移动平均线
m_cap = m_t/(1-(beta_1**t)) # 计算偏差校正后的估计
v_cap = v_t/(1-(beta_2**t)) # 计算偏差校正后的估计
theta_0_prev = theta_0
theta_0 = theta_0 - (alpha*m_cap)/(math.sqrt(v_cap)+epsilon) # 更新参数
if(theta_0 == theta_0_prev): # 检查是否收敛
break
总而言之,这个优化器目前是处于机器学习中最强的优化地位。
其实,对于不同的数据集或许会有所偏差,在不同的优化时间段,前中后期,各个优化器的准确率会有所波动,如下(源自论文)准确率测试图:
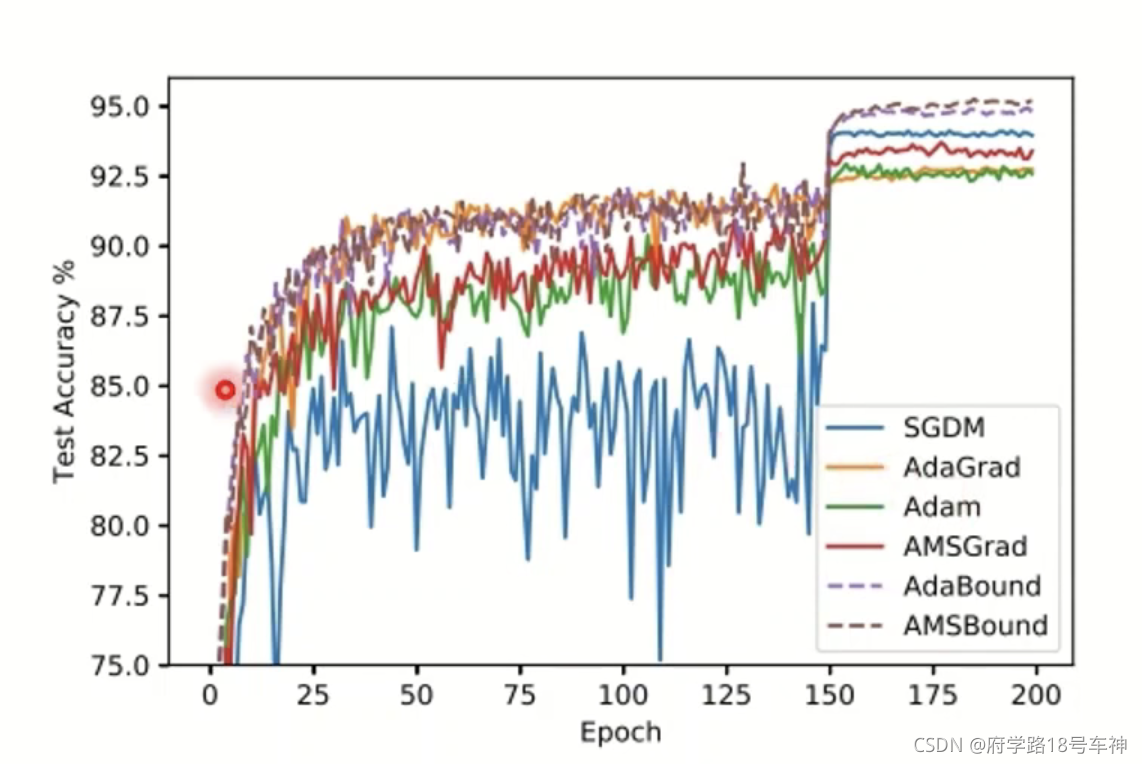
所以,不经感叹道,搞优化求解,真的是一门玄学啊,老的方法不一定在现在没有用,新的方法不一定适用于所以场景,找到最适合的方法才是真的有效的。相信在科技如此发达的现在及以后,会有更多的优化求解算法,推进人类进步,而不仅仅是从硬件上提升运算速度。
Recommend
推荐一本书,对于没学过最优控制或者最优化方法的小伙伴,会是一个很好地入门书籍。
《最优化计算方法》
真不是打广告,真诚推荐!!!
References
- https://github.com/Fafa-DL/Lhy_Machine_Learning
❤坚持读Paper,坚持做笔记,坚持学习❤!!!
⚡To Be No.1⚡⚡哈哈哈哈
学习DeepLearning坚持!30天计划!!!
打卡 第 4 /30 Day!!!
⚡创作不易⚡,过路能❤关注、收藏、点个赞❤三连就最好不过了
ღ( ´・ᴗ・` )
❤
『
Make the choice to be happy. The biggest part of being happy is to simply make up your mind to be a happy person.
』