背景
DFS 英文全称为(Depth First Search),中文简称深度优先搜索算法,其过程为沿着每一个可能的路径向下进行搜索,直到不能再深入为止,并且每一个节点只能访问一次。
算法的搜索遍历图的步骤
(1)首先找到初始节点A,
(2)依此从A未被访问的邻接点出发,对图进行深度优先遍历
(3)若有节点未被访问,则回溯到该节点,继续进行深度优先遍历
(4)直到所有与顶点A路径想通的节点都被访问过一次
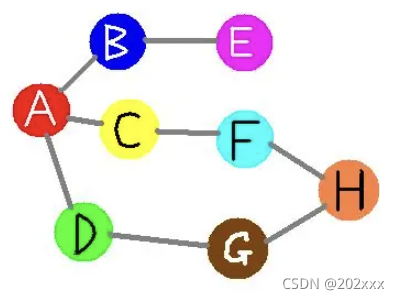
举个例子,在下方的无向连通图中,假设我们要从起始点A出发,使用深度优先搜索算法进行搜索,首先访问A->B->E,走不通了,回溯到A起始点,走第二个分支节点B,路径为A->C->F->H->G->D,走不通了,再回溯到起始点A,发现所有的节点都已经走过一次了,因此本次搜索结束。
DFS的应用
深度优先搜索算法常常被用于解决迷宫问题。
首先我们定义一个5*5的迷宫矩阵 maze
0 1 0 0 0
0 1 1 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0其中0代表迷宫走可以走的路,1代表迷宫中的墙壁
要求从左上角出发,走到左下角结束(0,0)出发,走到(4,4)
我们使用深度优先搜索算法进行求解
(1)从起始点(0,0)出发,第一步只能往下走(1,0),第二步走到交叉路口(2,0)
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
(2)由于出口在右下角,设定优先顺序,下>右>左>上
(3)走到(2,0)处开始往下走,直到走到(4,2)发现走不通
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
(4)此时回溯到上一节点(2,0),开始沿着另一个分支进行深度优先搜索
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
(5)在节点(2,4)中再次遇到分支,优先往下走,最终走到(4,4)走出迷宫
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
(6)因此最终走出迷宫的路径为:
(0,0)->(1,0)->(2,0)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)
(6)假设迷宫的出口在(2,0),则回溯到最近的未走过的分支顶点(2,4)往上走,最终走到终点
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
代码
def DFS(x, y):
if x <0 or x >= len(maze) or y < 0 or y >= len(maze[0]):#走出了迷宫墙外,不合法
return False
if maze_visit[x][y] == True:#防止走回头
return False
if maze[x][y] == 1:#标记为1的不能走
return False
maze_visit[x][y] = True#标记本次递归路线,防止走回头
if x == N and y == M:#走到终点停止递归
myStack.append((x,y))
return True
for m in move:#四个方向尝试走
next_x = x+m[0]
next_y = y+m[1]
if DFS(next_x, next_y):#判断能不能走通,能走通继续下一步递归
myStack.append((x,y))#将走通的路径记录下来
return True
return False
maze = [[0, 1, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0]]#定义迷宫
maze_visit = [[False, False, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False]]#记录路线是否已经走过,防止走反
move = [(0,1), (0,-1), (1,0), (-1,0)] #定义四个方向走的顺序
N, M = 4, 4 #定义出口的位置
myStack = []#记录走通的路径
DFS(0,0)#递归求解
myStack = myStack[::-1]#反转列表
for row in myStack:
print('(' + str(row[0]) + ','+ str(row[1]) + ')')输出迷宫路线
>>>move = [(0,1), (0,-1), (1,0), (-1,0)] #定义四个方向走的顺序
>>>N, M = 4, 4 #定义出口的位置
>>>myStack = []#记录走通的路径
>>>DFS(0,0)#递归求解
>>>myStack = myStack[::-1]#反转列表
>>>for row in myStack:
... print('(' + str(row[0]) + ','+ str(row[1]) + ')')
(0,0)
(1,0)
(2,0)
(2,1)
(2,2)
(2,3)
(2,4)
(3,4)
(4,4)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
变更出口位置
>>>move = [(0,1), (0,-1), (1,0), (-1,0)] #定义四个方向走的顺序
>>>N, M = 0, 2 #定义出口的位置
>>>myStack = []#记录走通的路径
>>>DFS(0,0)#递归求解
>>>myStack = myStack[::-1]#反转列表
>>>for row in myStack:
... print('(' + str(row[0]) + ','+ str(row[1]) + ')')
(0,0)
(1,0)
(2,0)
(2,1)
(2,2)
(2,3)
(2,4)
(1,4)
(0,4)
(0,3)
(0,2)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
递归的回溯过程
以入口为(0,0),出口为(0,2)为例,详细说一下递归的回溯过程
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
在代码中添加增加埋点,使每次发生递归时,对参数(x,y)进行输出
def DFS(x, y):
print("end:", str((x, y)))
if x <0 or x >= len(maze) or y < 0 or y >= len(maze[0]):#走出了迷宫墙外,不合法
print("False: 走出了迷宫墙外,不合法")
return False
if maze_visit[x][y] == True:#防止走回头
print("False: 往回走,不合法")
return False
if maze[x][y] == 1:#标记为1的不能走
print("False: 穿墙,不合法")
return False
maze_visit[x][y] = True#标记本次递归路线,防止走回头
if x == N and y == M:#走到终点停止递归
print("True: 到达终点")
myStack.append((x,y))
return True
for m in move:#四个方向尝试走
print("strat:", str((x,y)), "move:", str(m))
next_x = x+m[0]
next_y = y+m[1]
if DFS(next_x, next_y):#判断能不能走通,能走通继续下一步递归
myStack.append((x,y))#将走通的路径记录下来
return True
print("回溯上一节点")
return False创建好埋点后执行代码,输出如下:
>>>maze = [[0, 1, 0, 0, 0],
... [0, 1, 1, 1, 0],
... [0, 0, 0, 0, 0],
... [0, 1, 1, 1, 0],
... [0, 0, 0, 1, 0]]#定义迷宫
>>>maze_visit = [[False, False, False, False, False],
... [False, False, False, False, False],
... [False, False, False, False, False],
... [False, False, False, False, False],
... [False, False, False, False, False]]#记录路线是否已经走过,防止走反
>>>move = [(0,1), (0,-1), (1,0), (-1,0)] #定义四个方向走的顺序
>>>N, M = 0, 2 #定义出口的位置
>>>myStack = []#记录走通的路径
>>>DFS(0,0)#递归求解
end: (0, 0)
strat: (0, 0) move: (0, 1)
end: (0, 1)
False: 穿墙,不合法
回溯上一节点
strat: (0, 0) move: (0, -1)
end: (0, -1)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (0, 0) move: (1, 0)
end: (1, 0)
strat: (1, 0) move: (0, 1)
end: (1, 1)
False: 穿墙,不合法
回溯上一节点
strat: (1, 0) move: (0, -1)
end: (1, -1)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (1, 0) move: (1, 0)
end: (2, 0)
strat: (2, 0) move: (0, 1)
end: (2, 1)
strat: (2, 1) move: (0, 1)
end: (2, 2)
strat: (2, 2) move: (0, 1)
end: (2, 3)
strat: (2, 3) move: (0, 1)
end: (2, 4)
strat: (2, 4) move: (0, 1)
end: (2, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (2, 4) move: (0, -1)
end: (2, 3)
False: 往回走,不合法
回溯上一节点
strat: (2, 4) move: (1, 0)
end: (3, 4)
strat: (3, 4) move: (0, 1)
end: (3, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (3, 4) move: (0, -1)
end: (3, 3)
False: 穿墙,不合法
回溯上一节点
strat: (3, 4) move: (1, 0)
end: (4, 4)
strat: (4, 4) move: (0, 1)
end: (4, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (4, 4) move: (0, -1)
end: (4, 3)
False: 穿墙,不合法
回溯上一节点
strat: (4, 4) move: (1, 0)
end: (5, 4)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (4, 4) move: (-1, 0)
end: (3, 4)
False: 往回走,不合法
回溯上一节点
回溯上一节点
strat: (3, 4) move: (-1, 0)
end: (2, 4)
False: 往回走,不合法
回溯上一节点
回溯上一节点
strat: (2, 4) move: (-1, 0)
end: (1, 4)
strat: (1, 4) move: (0, 1)
end: (1, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (1, 4) move: (0, -1)
end: (1, 3)
False: 穿墙,不合法
回溯上一节点
strat: (1, 4) move: (1, 0)
end: (2, 4)
False: 往回走,不合法
回溯上一节点
strat: (1, 4) move: (-1, 0)
end: (0, 4)
strat: (0, 4) move: (0, 1)
end: (0, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (0, 4) move: (0, -1)
end: (0, 3)
strat: (0, 3) move: (0, 1)
end: (0, 4)
False: 往回走,不合法
回溯上一节点
strat: (0, 3) move: (0, -1)
end: (0, 2)
True: 到达终点接下来详细对每一步进行解析,先看方向依次为:右>左>下>上
move = [(0,1), (0,-1), (1,0), (-1,0)]第一步:(0,0)往右走到(0,1)穿墙,不合法,回溯到(0,0)
第二步:(0,0)往左走到(0,-1)走出了迷宫墙外,不合法,回溯到(0,0)
第三步:(0,0)往下走到(1,0)合法,将(1,0)作为起点,进入DFS(1,0)
end: (0, 0)
strat: (0, 0) move: (0, 1)
end: (0, 1)
False: 穿墙,不合法
回溯上一节点
strat: (0, 0) move: (0, -1)
end: (0, -1)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (0, 0) move: (1, 0)
end: (1, 0)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
第四步:(1,0)往右走到(1,1)穿墙,不合法,回溯到(1,0)
第五步:(1,0)往左走到(1,-1)走出了迷宫墙外,不合法,回溯到(1,0)
第六步:(1,0)往下走到(1,0)合法,将(2,0)作为起点,进入DFS(2,0)
strat: (1, 0) move: (0, 1)
end: (1, 1)
False: 穿墙,不合法
回溯上一节点
strat: (1, 0) move: (0, -1)
end: (1, -1)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (1, 0) move: (1, 0)
end: (2, 0)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
第七步:(2,0)往右走到(2,1)合法,将(2,1)作为起点,进入DFS(2,1)
第八步:(2,1)往右走到(2,2)合法,将(2,2)作为起点,进入DFS(2,2)
第九步:(2,2)往右走到(2,3)合法,将(2,3)作为起点,进入DFS(2,3)
第十步:(2,3)往右走到(2,4)合法,将(2,4)作为起点,进入DFS(2,4)
第十一步:(2,4)往右走到(2,5)走出了迷宫墙外,不合法,回溯到(2,4)
第十二步:(2,4)往左走到(2,3)往回走,不合法,回溯到(2,4)
第十三步:(2,4)往下走到(3,4)合法,将(3,4)作为起点,进入DFS(3,4)
strat: (2, 0) move: (0, 1)
end: (2, 1)
strat: (2, 1) move: (0, 1)
end: (2, 2)
strat: (2, 2) move: (0, 1)
end: (2, 3)
strat: (2, 3) move: (0, 1)
end: (2, 4)
strat: (2, 4) move: (0, 1)
end: (2, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (2, 4) move: (0, -1)
end: (2, 3)
False: 往回走,不合法
回溯上一节点
strat: (2, 4) move: (1, 0)
end: (3, 4)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
第十四步:(3,4)往右走到(3,5)走出了迷宫墙外,不合法,回溯到(3,4)
第十五步:(3,4)往左走到(3,3)往回走,不合法,回溯到(3,4)
第十六步:(3,4)往下走到(4,4)合法,将(4,4)作为起点,进入DFS(4,4)
strat: (3, 4) move: (0, 1)
end: (3, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (3, 4) move: (0, -1)
end: (3, 3)
False: 穿墙,不合法
回溯上一节点
strat: (3, 4) move: (1, 0)
end: (4, 4)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
第十七步:(4,4)往右走到(4,5)走出了迷宫墙外,不合法,回溯到(4,4)
第十八步:(4,4)往左走到(4,3)穿墙,不合法,回溯到(4,4)
第十九步:(4,4)往下走到(4,4)走出了迷宫墙外,不合法,回溯到(4,4)
第十九步:(4,4)往上走到(3,4)往回走,不合法,回溯到(4,4)
第二十步:此时四个方向都走不通,因此回溯到上一个交叉路口(3,4),在第十四到第十八步(3,4)节点已经往右,左,下三个方向走过一次了(move循环到了第三位),因此只剩往上走一种选择,(3,4)往上走到(2,4)往回走,不合法,回溯到(2,4)
第二十一步:同理(2,4)在第十一到第十三步已经往右,左,下三个方向走过一次了,因此只剩往上走一种选择,(3,4)往上走到(1,4),合法,将(1,4)作为起点,进入DFS(1,4)
strat: (4, 4) move: (0, 1)
end: (4, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (4, 4) move: (0, -1)
end: (4, 3)
False: 穿墙,不合法
回溯上一节点
strat: (4, 4) move: (1, 0)
end: (5, 4)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (4, 4) move: (-1, 0)
end: (3, 4)
False: 往回走,不合法
回溯上一节点
回溯上一节点
strat: (3, 4) move: (-1, 0)
end: (2, 4)
False: 往回走,不合法
回溯上一节点
回溯上一节点
strat: (2, 4) move: (-1, 0)
end: (1, 4)| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
从(1,4)开始到达终点的步骤再次就不进行详细解析了~~~(同理)最终到达终点(0,2)
strat: (1, 4) move: (0, 1)
end: (1, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (1, 4) move: (0, -1)
end: (1, 3)
False: 穿墙,不合法
回溯上一节点
strat: (1, 4) move: (1, 0)
end: (2, 4)
False: 往回走,不合法
回溯上一节点
strat: (1, 4) move: (-1, 0)
end: (0, 4)
~~~~~~~~~~~~~~~~~~~~
strat: (0, 4) move: (0, 1)
end: (0, 5)
False: 走出了迷宫墙外,不合法
回溯上一节点
strat: (0, 4) move: (0, -1)
end: (0, 3)
~~~~~~~~~~~~~~~~~~~~
strat: (0, 3) move: (0, 1)
end: (0, 4)
False: 往回走,不合法
回溯上一节点
strat: (0, 3) move: (0, -1)
end: (0, 2)
True: 到达终点!!!!!!!!!!!!!!!!!!递归结束!!!!!!!!!!!!!!!!!!!!
使用递归求解的案例
匈牙利算法寻找最大匹配_202xxx的博客-CSDN博客
【牛客网华为机试】HJ28 素数伴侣_202xxx的博客-CSDN博客
【牛客网华为机试】HJ43 迷宫问题_202xxx的博客-CSDN博客