---

---

前言

递归非常重要，有时也非常晦涩难懂，它们常以简单的代码解决复杂的问题，在很多时候非常适用，让我们一起来了解一下，并解决几个递归的经典问题吧。

---

一、什么是递归？

首先让我们来了解一下什么是递归，它有什么条件。

程序调用自身的编程技巧称为递归（ recursion）。 递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。 递归的主要思考方式在于：把大事化小

递归的两个必要条件:

• 存在限制条件，当满足这个限制条件的时候，递归便不再继续。
• 每次递归调用之后越来越接近这个限制条件。

在写递归函数时需要切记这两个条件。
递归也要考虑栈溢出等问题，比如斐波那契数列数列的递归实现。

二、汉诺塔问题

1.问题描述

传说婆罗门庙里有一个塔台,台上有 3 根标号为 A,B,C的用钻石做
成的柱子,在 A 柱上放着 64 个金盘,每一个都比下面的略小一点。把 A 柱上的金盘全部移到C柱上的那一天就是世界末日。移动的条件是：一次只能移动一个金盘,移动过程中大金盘不能放在小金盘上面。庙里的僧人一直在移个不停。因为全部的移动是2^63次,如果每秒移动一次的话,需要 500 亿年。

动图演示

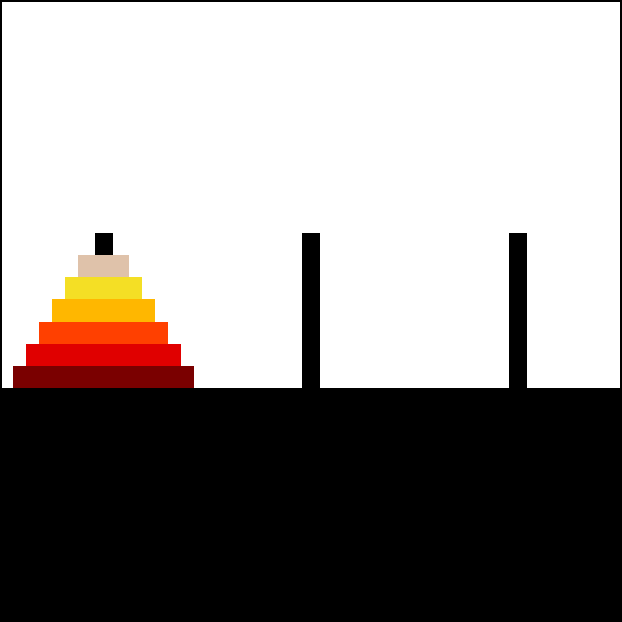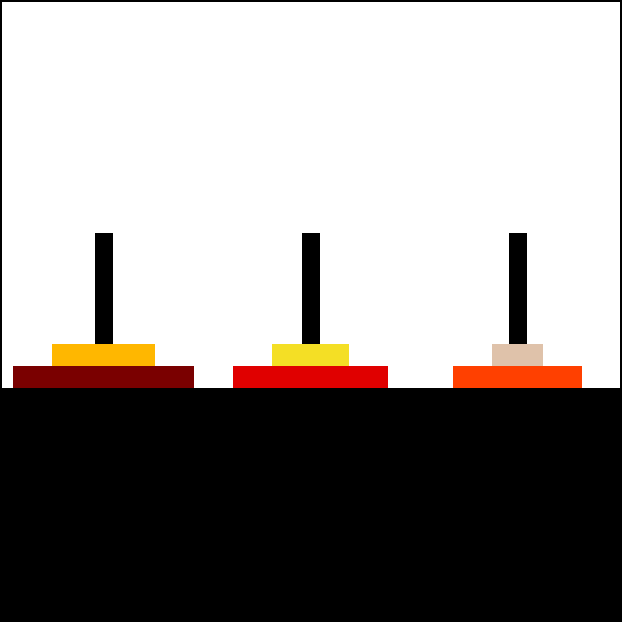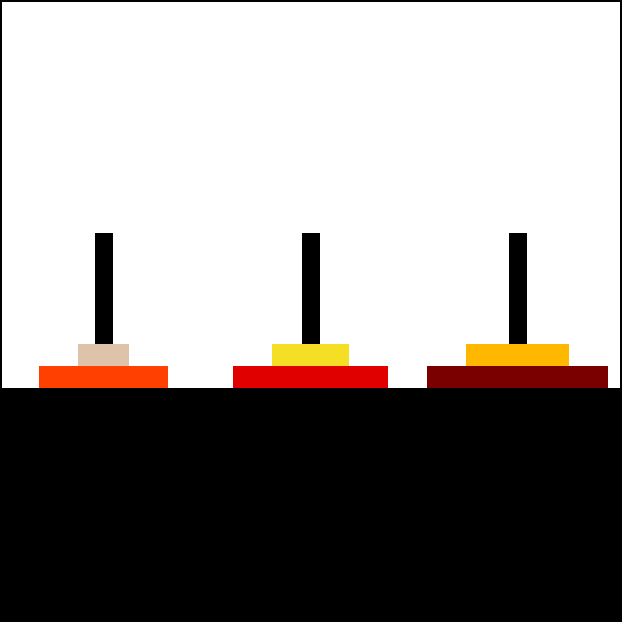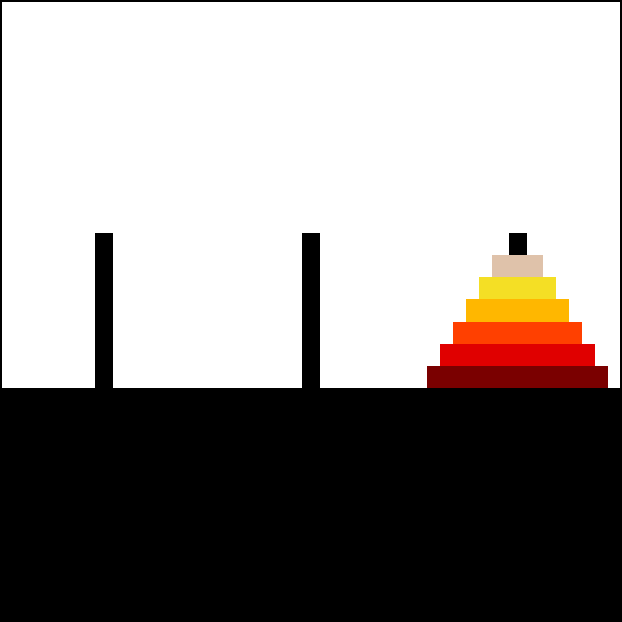
2.问题分析

设最初的盘子总数为n

1. 用C 柱做过渡,将 A 柱上的(n-1)个盘子移到 B 柱上
2. 将 A 柱上最后一个盘子直接移到C 柱上
3. 用 A 柱做过渡,将 B 柱上的(n—1)个盘子移到 C 柱上

当n=3时：
看一下示例图

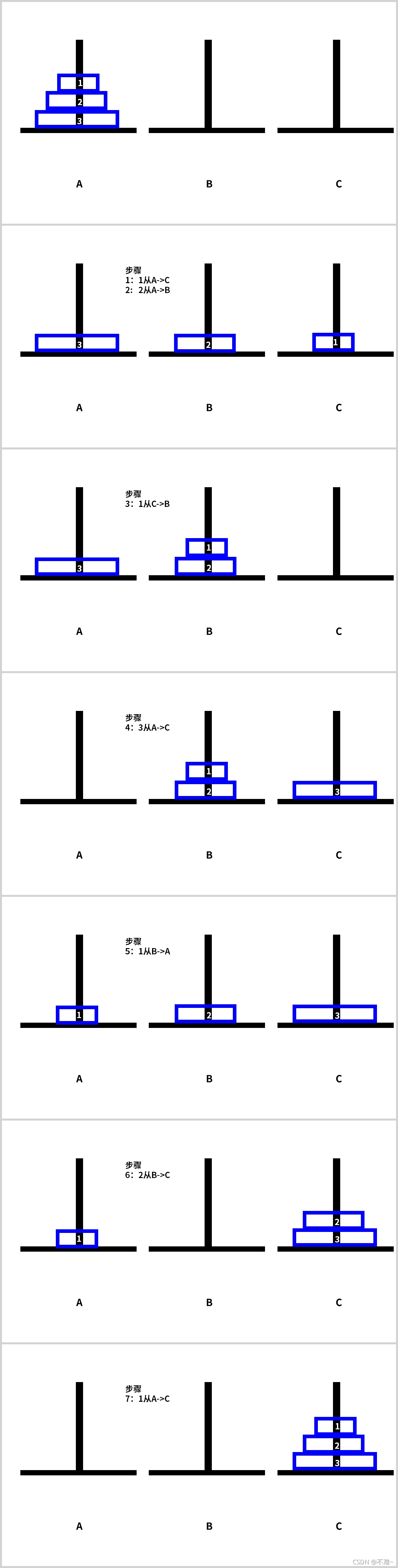
利用这个解法，
将移动n 个盘子的汉诺塔问题归结为移动(n-1)个盘子的汉诺塔问题。与此类似,移动(n-1)个盘子的汉诺塔问题又可归结为移动(n-2)个盘子的汉诺塔问题……最后总可以归结到只移动一个盘子的汉诺塔问题,这样问题就解决。

3.代码实现

#include<stdio.h>
void Hanoi(int n, char a ,char b ,char c)
{
	if (n == 1)
	{
		printf("%c->%c\n", a , c);//只有一个盘子，直接移动到C
	}
	else
	{
		Hanoi(n - 1,a ,c ,b );//将A上面n-1个盘子移动到B中
		printf("%c->%c\n", a ,c);//将A最后一个移动到C
		Hanoi(n - 1, b, a, c);//将B上的n-1个盘子移到C上
	}
}

int main()
{

	char a = 'A';
	char b = 'B';
	char c = 'C';
	Hanoi(3,a,b,c);
	return 0;
}

三、青蛙跳台阶问题

暂不考虑特别大的数使栈溢出。
对于青蛙跳台阶，由于步骤较多，难以画图，我们采用数学推理的方法，求得相关递推公式。

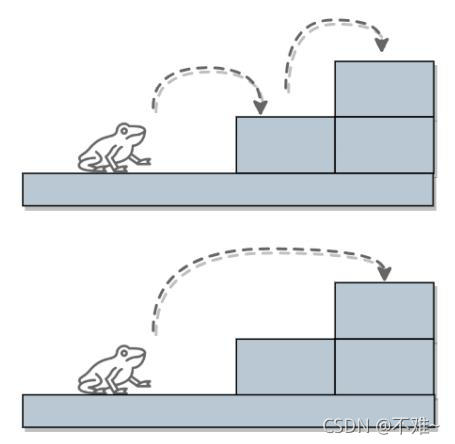
问题一

1.问题描述

1. 一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

2.问题分析

当n = 1，只有一种跳法，那就是1
当n = 2，那么有两种跳法，2，[1, 1]
当n = 3，那么有三种跳法，[1, 1, 1], , [1, 2], [2, 1]
当n = 4，那么有五种跳法，[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [2, 1, 1], [2, 2]
当n = 5，那么有八种跳法，[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 1, 2, 1], [1, 2, 1, 1], [2, 1, 1, 1], [2, 2, 1], [2, 1, 2], [1, 2, 2]
结果为1，2，3，5，8
有没有感觉很眼熟
没错，这就是一个斐波那契数列，所以问题很快可以解决。

3.代码实现

//递归做法：

int RJump1(int n)
{
	if (n == 0)
		return 0;
	if (n == 1)
		return 1;
	if (n == 2)
		return 2;
	//n>2
	return RJump1(n - 1) + RJump1(n - 2);
}


//非递归做法：

int  Jump1(int n)
{
	if (n == 0)
		return 0;
	if (n == 1)
		return 1;
	if (n == 2)
		return 2;
	int a1 = 1;
	int a2 = 2;
	int a3;
	for (int i = 3; i <= n; i++)
	{
		a3 = a1 + a2;
		a1 = a2;
		a2 = a3;
	}
	return a3;
}

问题二

1.问题描述

2. 一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

2.问题分析

如果台阶级数为n的话，这时我们把n级台阶时的跳法看成n的函数，记函数关系为F，第一次跳的时候有n种不同的选择：

• 若是第一次跳一级，此时跳法的数目等于后面剩下的n-1级台阶的跳法数目，即为F(n-1)。
• 若是第一次跳m(m<n)级，此时跳法的数目等于后面剩下的n-m级台阶的跳法数目，即为F(n-m)。
• 若是第一次跳n-1级，此时跳法的数目等于1，从0跳到n-1阶，再从n-1到n，虽然跳了两次，但是跳法为1，只有一种方法，此时F(n-n+1)=F(1)=1。
• 若是第一次跳n级，此时跳法的数目等于1，即F(n-n)=F(0)=1。

第三种情况比较难以想到，我也是想了很久才想明白。
所以当台阶为n时总次数为

F(n)=F(n-1)+F(n-2)……+F(1)+F(0)
令n=n-1
此时最多第一次跳n-1次
F(n-1)=F(n-2)……+F(0)
两式相减即可得到
F(n)=2*F(n-1)

我们得到了递推公式，以及F(1)=F(0)=1。
但是当n=1时不满足递推公式，所以当n=1时返回1即可。
跳法为1，1，2，4，8……
其实可以由递推公式看出是一个等比数列，可以算出它的和2^n-1。

3.代码实现

int RJump2(int n)
{
	//因为递推公式只需要找到它前一项，即F(n-1)的值就可以返回，我们指定n=1是1种，是已经确定的值，到n=1即可结束
	if (n == 1)
		return 1;
	//当阶数大于1时可以用递推公式
	return 2 * RJump2(n - 1);
}

直接使用公式即可。代码简单得让人害怕。

问题三

1.问题描述

3. 一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上m级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

2.问题分析

同样我们采用问题2的方法，使用函数推理
当m<n时，即能跳的最大级数小于总台阶数
所以自变量最大只能到n-m，即函数为F(n-m)

F(n)=F(n-1)+F(n-2)……+F(n-(m-1)) +F(n-m)
令n=n-1
F(n-1)=F(n-2)……+F(n-m)+F(n-m)
解释：因为n>m，即n-m>0，又因为他们是整数，所以n-m>=1，所以当n=n-1时，它能走的最大阶数仍为m，所以比较F(n)，F(n-1)有两项F(n-m)
两式相减即可得到
F(n)=2*F(n-1)-F(n-m)

这简直就是在做数学。
当m>=n时，即能跳的最大级数大于等于总台阶数，这时我们采用解决问题二的公式即可。

3.代码实现

//n为总阶数，m为能跳的最大阶数
int RJump3(int n, int m)
{
	//
	if (n == 1)
		return 1;
	//当m小于n时可采用上述递推公式
	if (m < n)
	{
		return 2 * RJump3(n - 1, m) - RJump3(n - m, m);
	}

	//当m大于等于n时可采用第二题的公式
	else
	{
		//注意此时传参，青蛙能跳的阶数最大只能为总的阶数,即n
		return 2 * RJump3(n - 1, n);
	}
}


void test()
{
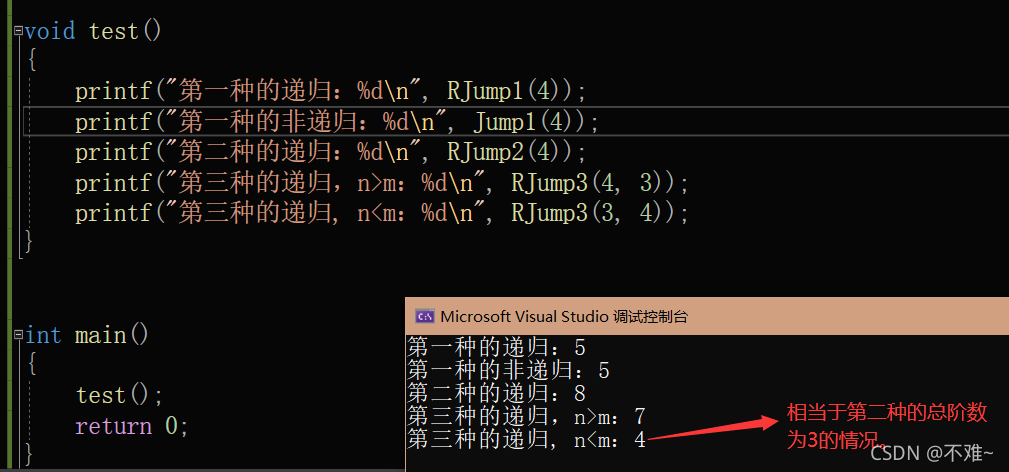
	printf("第一种的递归：%d\n", RJump1(4));
	printf("第一种的非递归：%d\n", Jump1(4));
	printf("第二种的递归：%d\n", RJump2(4));
	printf("第三种的递归，n>m：%d\n", RJump3(4, 3));
	printf("第三种的递归, n<m：%d\n", RJump3(3, 4));
}

int main()
{
	test();
	return 0;
}

---

总结

不得不说，数学很重要，即使在数学中较为简单的运算，用在具有特定场景前，并用代码实现，还是很有挑战的。如有错误，欢迎大佬指正。