零.前言
所谓KMP算法是进行字符串匹配的一个优秀算法,整体理解起来其实并不是十分困难,主要的难点在于next数组的创建上,但其实暴力创建也未为不可,因为模式字符串通常来讲也不是特别长,它最大的特点就在于主串的指针不需要返回,从而降低了算法的复杂度。
1.什么是KMP算法
KMP算法是一种字符串匹配算法,即在主字符串查找模式字符串(简单来说就是判断一个字符串中是否包含另一个字符串),是C语言库函数strstr的算法优化。
2.通常情况下的字符串匹配
首先来讲一讲不用KMP算法的字符串匹配,便于理解之后KMP算法,和KMP算法的优势。
首先建立一个字符串作为主串:
char a[]="abcbabc";这个字符串在内存中是这样存放的:
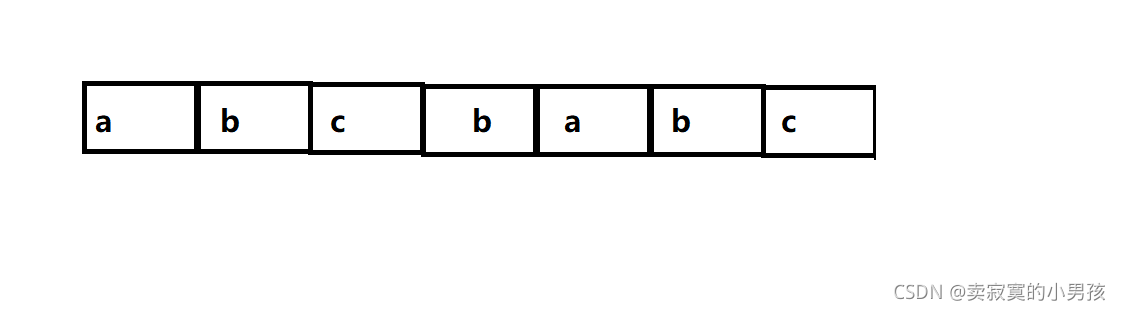
假设现在要在这个字符串中查找字符串"ba"。即我们也要定义一个数组来放"bca"。b[2]="bca"。
我们把这两个内容放在同一张图里。
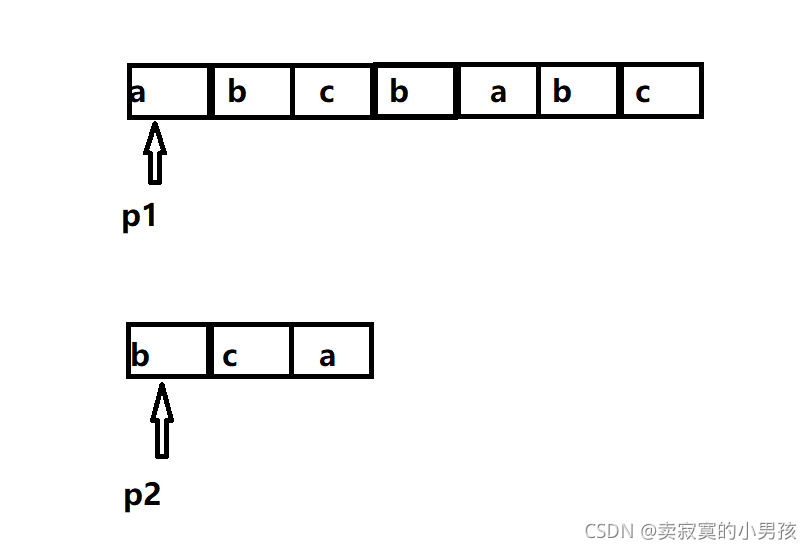
p1,p2分别为指向两个字符串首元素地址的指针。
第一步比较的是a[0]与b[0]。 发现两者不相等,p2指针不动,p1+1指向a[1],此时发现两者相等。p1和p2指针都+1,p1指向a[2],p2指向b[1]。
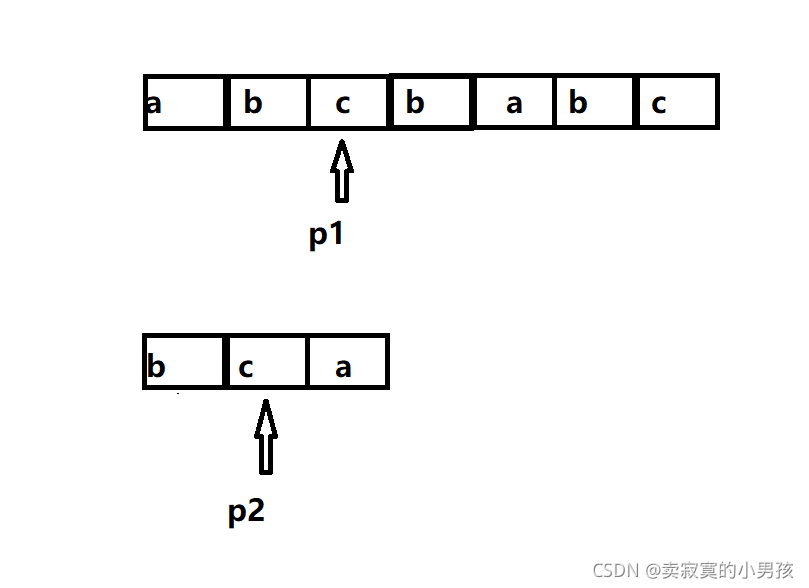
发现依然相等,则p1和p2继续++
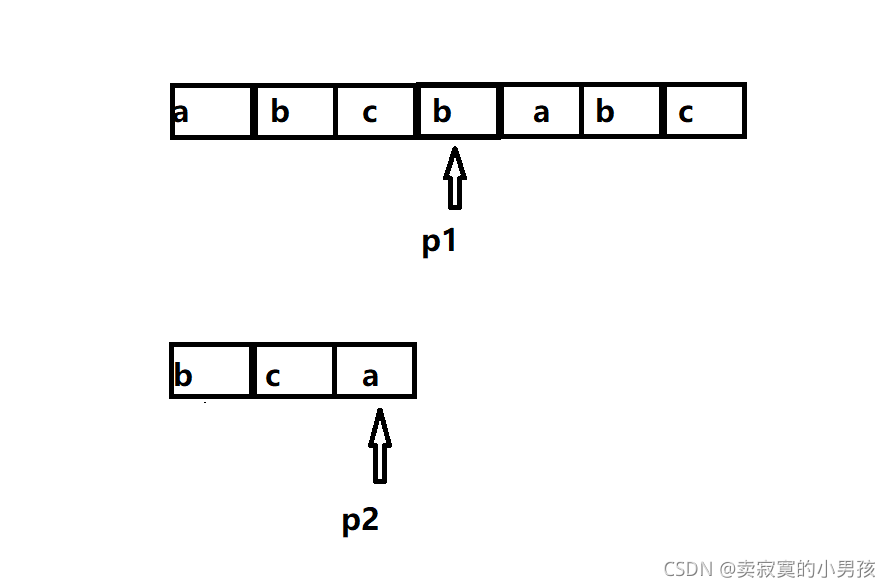
此时发现两者不相等,p2需要退回起始位置即b[0],p1需要退回第一次匹配成功时的下一个位置,即a[2]。再重复这一过程。
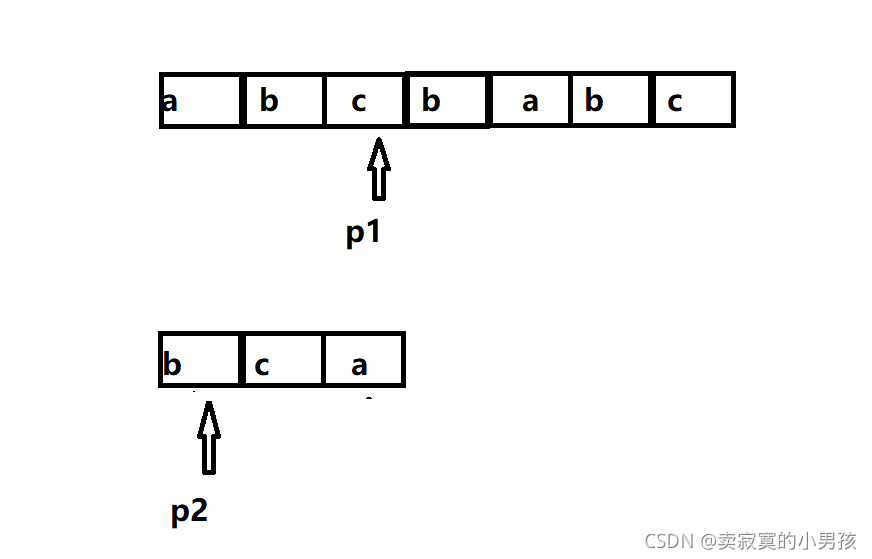
算法大佬们发现这样计算太麻烦,于是考虑能不能在匹配失败之后不用移动p1指针,只移动p2指针来达到同样的效果呢?于是KMP算法就诞生了。
3.用KMP算法进行字符串匹配
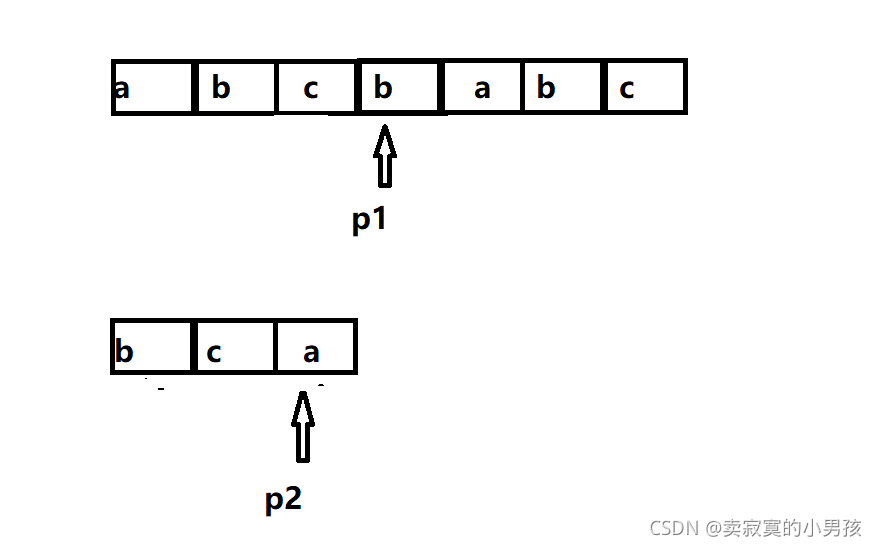
在这里我们发现a[3]与b[2]不同时,我们已经进行了两次匹配,即p1之前的两个元素与p2之前的两个元素是相同的。那么此时的p1就不需要回到a[2]了,直接用b[2]与a[3]比较就可以了。
这个例子看起来不明显,我们来看一个别的例子。
我们建立这两个数组,在主串中查找模式字符串。我们依然记主串为a[],模式匹配字符串为b[]。
p1为指向主串首元素地址的指针,p2为指向模式字符串首元素地址的指针。
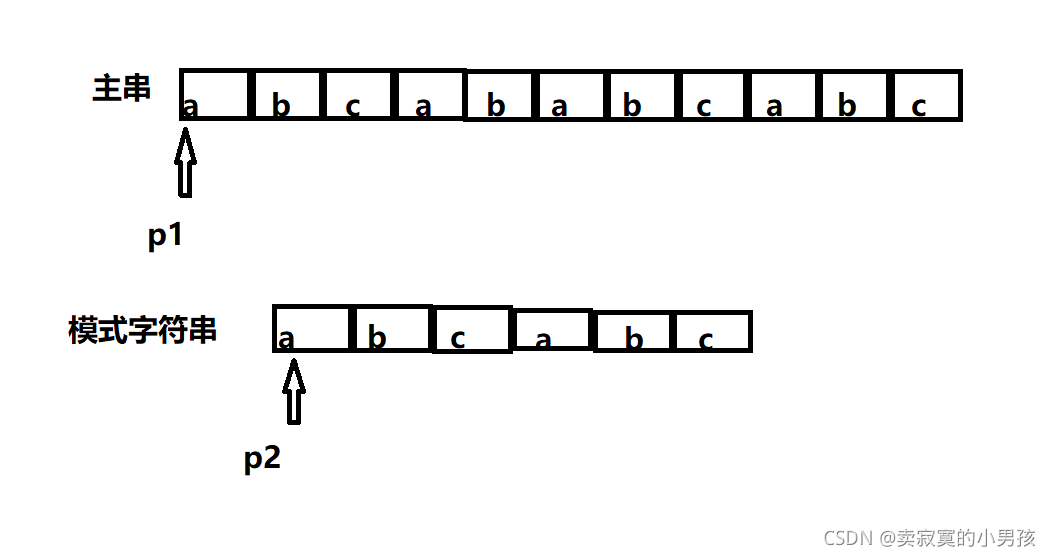
从第一个字符开始,我们可以匹配到5个元素,即abcab,此时指针的情况是这样的:
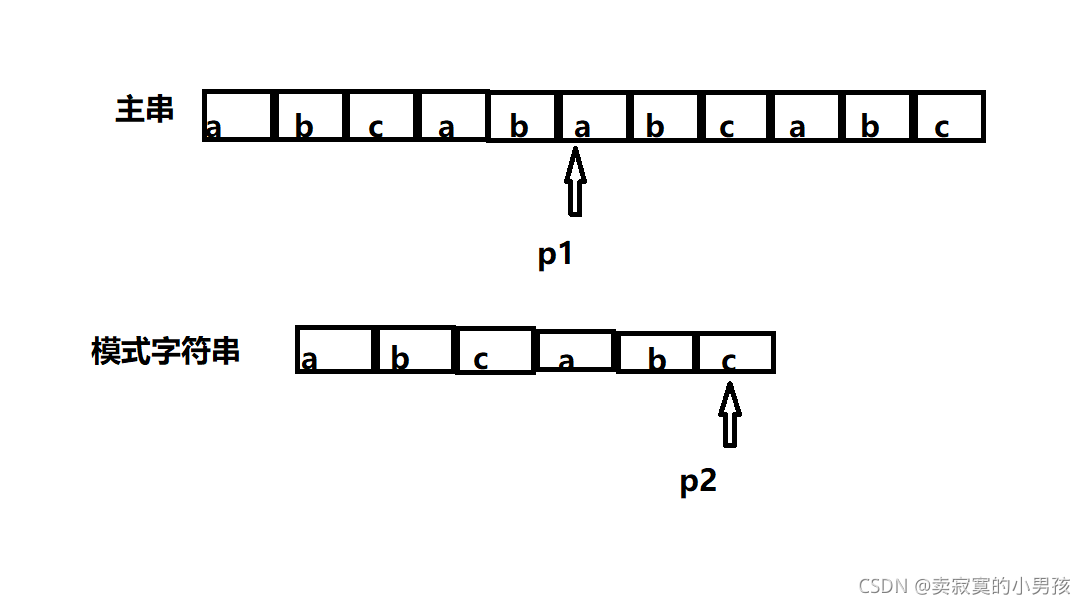 此时发现所比较的字符是不同的,但我们已经比较了5次了,且前五次元素是相同的。即不同元素的前五个元素是什么,我们是清楚的,就是模式字符串的前五个元素。
此时发现所比较的字符是不同的,但我们已经比较了5次了,且前五次元素是相同的。即不同元素的前五个元素是什么,我们是清楚的,就是模式字符串的前五个元素。
我们需要记住,我们的目的就是让p1指针不移动,而p1是用来比较的,即相当于假设此时p1所指向的元素是模式字符串中的一个字符,在p1所指向的字符前面一定有除了第一次匹配成功的首元素字符的另一个与模式字符串相同的字符,很有可能以该元素为首的又一个字符串和模式字符串是相同的。
简洁来说,就是从p1开始向前寻找与模式字符串首元素相同的字符,再从这一字符开始看是否可以找到一个和模式字符串相同的字符串。
用这道题举例,此时向前看,发现除了第一个元素之外a[3]也是a,我们将模式字符串的首元素与这个a对齐再进行比较。
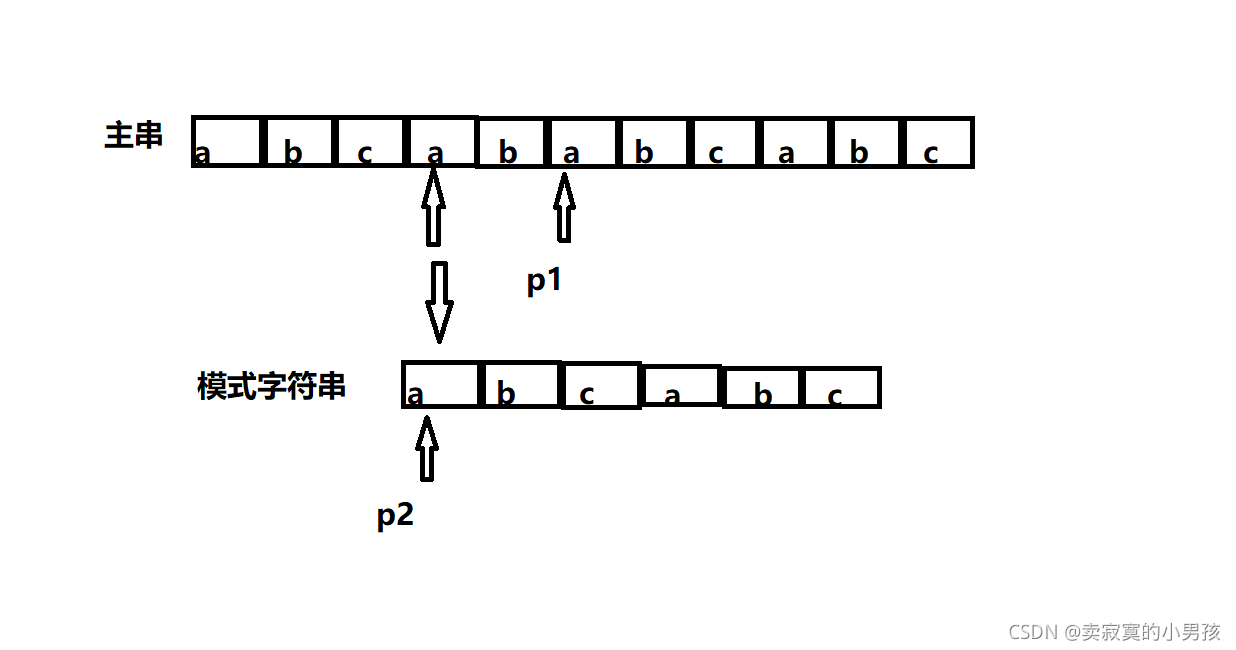
即从两个箭头处开始。画个图是不是就清晰了很多呀。我们已经知道在p1前面的两个元素是相同的了,那么只需要比较p1与b[2]即可,所以p2指针只需要移动到b[2]处即可。
由于p1向前寻找的字符个数是不可能大于模式字符串的,所以向前查找的首元素(如果找到的话),一定是在模式字符串中的。
因此在哪里出现匹配失败,p2指针所返回的位置是固定的,且是与主串无关的。
那么我们就可以建立一个数组,数组的下标记录匹配不成功的位置,数组的内容是返回的位置。数组的长度就是模式字符串数组的长度。
对于这样一个字符串
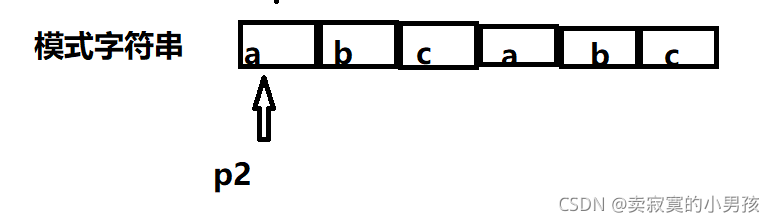
我们建立一个next数组。
我们规定next[0]中存放的内容是0(这不是随便规定的,以后会有用处),当第一个元素匹配失败时,很显然p2应该返回最起始的元素0,即next[1]=0。
当第二个元素匹配失败时,此时说明第一个元素匹配成功了,向前看发现只有一个a且为起始元素,所以p2应该返回最起始的元素0,即next[2]=0。
当第三个元素匹配失败时,此时第一第二个元素已经匹配成功,在这两个元素中找首元素,发现只有第一个元素是首元素,所以p2应该返回最起始的0,即next[3]=0。
当第四个元素匹配失败时,此时第一二三个元素已经匹配成功,在这三个元素中找首元素,发现只有第一个元素是首元素,所以p2依然返回最起始的0,即next[4]=0。
当第五个元素匹配失败时,此时第一二三四个元素已经匹配成功,在四个元素中找首元素,发现除了第一个元素,第四个元素也是首元素,从该元素向后数,发现只有一个元素即它本身与字符串部分相等。所以返回第二个元素即next[5]=1。
当第六个元素匹配失败时,此时第一二三四五个元素匹配成功,在这五个元素中找首元素,发现除了第一个元素第四个元素也是首元素,比较前两个元素。
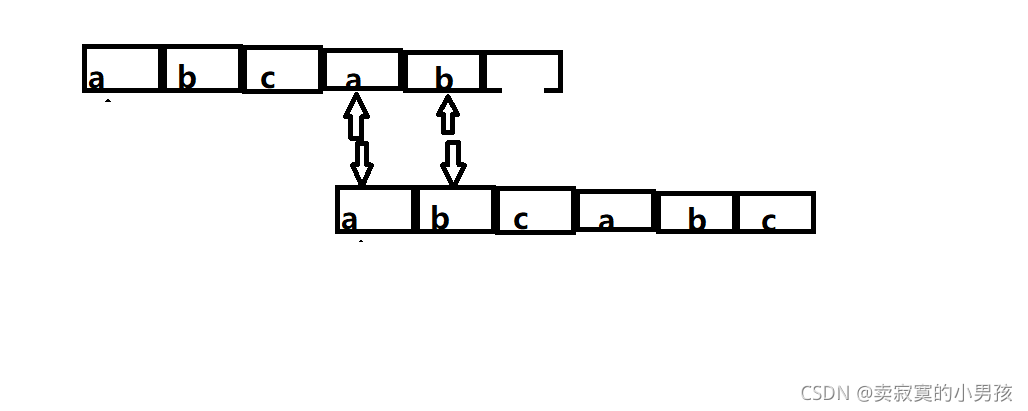
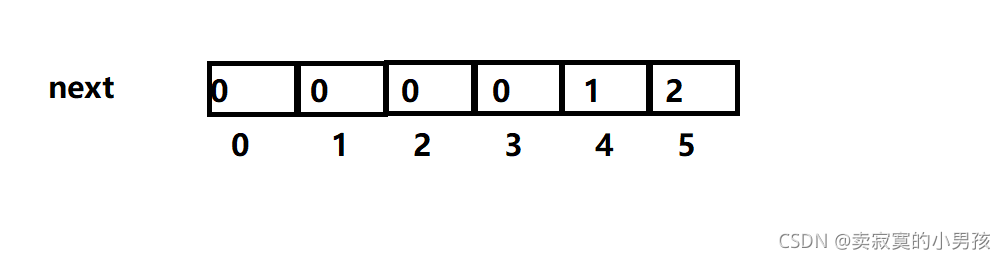
我们发现前两个元素是一样的,只需要比较第三个,即next[6]=2。
所以next数组我们就创建成功了
4.优化next数组的创建
我们发现,当返回值不是0的时候,整个模式字符串中一定有以除了以首元素开始的和首元素相同的字符的字符串与模式字符串的前几项对应。且该字符串的最后一个字符一定是匹配失败的前一个字符。
假设模式字符串在第i项匹配失败了,p2返回了第k项。
那么就存在p[0]p[1]p[2]……p[k-2]=p[i-k]p[i-k+1]……p[i-2]。
1.当p[i-1]=p[k-1]的时候:
此时p[0]p[1]p[2]……p[k-2]p[k-1]=p[i-k]p[i-k+1]……p[i-2]p[i-1]。
这说明如果在第i+1项匹配失败了,p2会返回第k+1项。即next[i]=next[i-1]+1。
2.当p[i-1]!=p[k-1]时,
此时讲将回p[k-1]所对应的退回值加一,即观察p[next[k-1]]是否和p[i-1]相等,若相等则next[i]=next[k-1]+1,如果依然不相等但是next[k-1]=0,则next[i]=0,如果不等继续按这个规律退回,直到相等为止。
5.next数组创建的举例
1.ababcabcdabcde
1.首先将next[0]置为0,即next[0]=0。
显然next[1]=0,next[2]=0,next[3]=1。
当比较第五项时,此时i=4,k=2,此时p[3]=p[1],所以next[4]=next[3]+1=2。
比较第六项时,此时i=5,k=3,此时p[4]!=p[2],所以比较p[next[2]]和p[4],发现两者依然不相等,但是p[next[2]]=0所以next[5]=0。
第七项,i=6,k=1,此时p[5]=p[0],所以next[6]=next[5]+1=1。
第八项,i=7,k=2,此时p[6]=p[1],所以next[7]=next[6]+1=2。
第九项,i=8,k=3,此时p[7]!=p[2],所以比较p[next[2]]和p[7],发现两者不等,但是next[2]=0,所以next[8]=0。
第十项,i=9,k=1,此时p[8]!=p[0],所以比较p[next[0]]和p[8],发现两者不等,但是next[0]=0,所以next[9]=0。
第十一项,i=10,k=1,此时p[9]=p[0],所以next[10]=next[9]+1=1。
第十二项,i=11,k=2,此时p[10]=p[1],所以next[11]=next[10]+1=2。
第十三项,i=12,k=3,此时p[11]!=p[2],所以比较p[next[2]]和p[11],发现两者不等,但是next[2]=0,所以next[12]=0。
第十四项,i=13,k=1,此时p[12]!=p[0],所以比较p[next[0]]和p[12],发现两者不等,但是next[0]=0,所以next[13]=0。
至此next数组创建完毕
为next[13]={0,0,0,1,2,0,1,2,0,0,1,2,0,0}。
2.abcabcabcabcdabcde
首先将next[0]置为0,即next[0]=0。
显然next[1]=0,next[2]=0,next[3]=0
第五项,i=4,k=1,p[3]=p[0],所以next[4]=next[3]+1=1。
第六项,i=5,k=2,p[4]=p[1],所以next[5]=next[4]+1=2。
第七项,i=6,k=3,p[5]=p[2],所以next[6]=next[5]+1=3。
第八项,i=7,k=4,p[6]=p[3],所以next[7]=next[6]+1=4。
第九项,i=8,k=5,p[7]=p[4],所以next[8]=next[7]+1=5。
第十项,i=9,k=6,p[8]=p[5],所以next[9]=next[8]+1=6。
第十一项,i=10,k=7,p[9]=p[6],所以next[10]=next[9]+1=7。
第十二项,i=11,k=8,p[10]=p[7],所以next[11]=next[10]+1=8。
第十三项,i=12,k=9,p[11]=p[8],所以next[12]=next[11]+1=9。
第十四项,i=13,k=10,p[12]!=p[9],所以比较p[next[9]]与p[12],发现依然不相等,且next[9]=6,此时比较p[next[6]]与p[12],发现依然不等,next[6]=4,此时比较p[next[4]]与p[12],发现还是不等,next[4]=1,此时比较p[next[1]]与p[12],仍然不等,但是next[1]=0,所以next[13]=0。
第十五项,i=14,k=1,p[13]=p[0],所以next[14]=next[13]+1=1。
第十六项,i=15,k=2,p[14]=p[1],所以next[15]=next[14]+1=2。
第十七项,i=16,k=3,p[15]=p[2],所以next[16]=next[15]+1=3。
第十八项,i=17,k=4,p[16]!=p[3],所以比较p[next[3]]与p[16]发现两者不等,next[3]=0,所以p[17]=0。
6.C语言代码实现
#include<stdio.h>
#include<string.h>
void Get_Nextarray(char str[],int len,int next[]) //获取字符串str[]的前缀表next[]
{
int i,j;
i=0; j=1; //初始化
next[0]=0;
for(j=1; j<=len-1; j++) //for循环,控制j向后
{
if (str[i]==str[j]) //相同:i后移
{
i++;
}
else if (str[i]!=str[j]) //不相同
{
while(str[i]!=str[j] && i>=1) //i持续退位(注意i>=1的限制)
{
i=next[i-1]; //看i所指元素的前一个元素的next值
}
}
else continue;
next[j]=i; //赋值
}
}
int main(void)
{
/*子串前缀表测试程序
int n;
scanf("%d",&n);
getchar();
char str[n],next[n];
gets(str);
Get_Nextarray(str,n,next);
int i;
for (i=0; i<=n-1; i++)
{
printf("%d ",next[i]);
}
*/
char str[1000]; //长串
char ch[1000]; //子串
printf("Please input Long String:"); gets(str);
printf("Please input Substring:"); gets(ch);
printf("\n-------------------------------------\n");
int LEN=strlen(str);
int len=strlen(ch);
int next[len]; //子串前缀表
Get_Nextarray(ch,len,next);
int i,j; //i遍历长串str,j遍历子串ch
i=j=0;
int flag=0; //标志变量
while(j<=len-1)
{
if (j==len-1 && str[i]==ch[j]) //一次匹配完,输出位置,继续往后匹配
{
printf("Found the pattern at : %d -> %d \n",i-j+1,i+1); //输出位置(+1是为了看得舒服,按数组来说位置是i-j)
j=next[j-1];
flag++;
}
if (str[i]==ch[j]) //相同则往后继续遍历
{
i++;
j++;
}
else //不相同,则j控制的子串需要跳转
{
if (j==0) //特殊情况是j回到了头也无法匹配,这个时候只要i移动了
{
j=0;
i++;
}
else
{
j=next[j-1];
}
}
if (i==LEN-1) break;
}
//出循环后,如果标志变量为0,说明一次也没有匹配到。反之已经匹配到。
if (flag==0)
{
printf("Not Found!\n\n");
}
else
{
printf("Found the pattern %d time(s) in the string!\n\n",flag);
}
return 0;
}
找了一份比较优秀的代码,我自己就不敲了奥。。注释也都很详细。
7.总结
KMP有的地方是不太好理解,但是也经不住你的经常练习呀,之前看到的鸡汤说,一个人要办好一件事要经过五种境界,分别是:初步的了解,开始使用,重复,融会贯通,进一步加强。看完这篇文章之后也只是第一种境界,还需要以后持续不断地练习才能彻底掌握,这个时候你会发现KMP算法,真香。
