该笔记初衷为期末复习所用,引用出处均已注明,涉及个人理解部分如果有不对之处,还请批评指正,俺会虚心接受滴!
1.应用范围
目标函数的无约束绩效问题。
2.相关定义
定义1 设Q为n阶实对称正定矩阵,若n维方向x和y满足,则称方向x和y是Q-共轭的。
3.原理
将函数改写成如下形式:
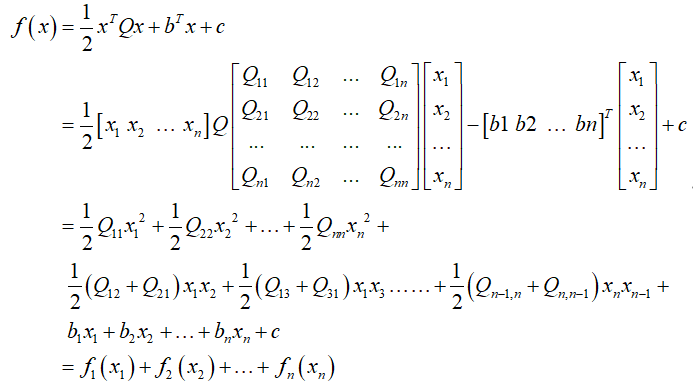
如果每个子函数都能取得最小值,那么f(x)也能取得最小值。假设梯度下降一共需要n阶(也就是迭代次数啦),每个
对应一个阶梯,每阶的方向和步长都使
取得最小值。
我们当然希望阶梯数n越少越好,那么如何找到所需最少的阶梯数呢?当阶梯数最少时,每阶的方向和步长都不同,且每阶都无法由其他的阶梯组合而成。也就是说,每次梯度下降的方向必须是线性无关的,梯度下降的次数才会最少,迭代次数才会最少。
我们是有办法找到一组线性无关的方向向量(即Rn中的一组基{p1,p2,…,pn})的哦!首先在初始点(记为x1)选取负梯度方向为p1(就是x1点的方向啦),然后寻找与p1共轭的方向为p2,再寻找与p1和p2共轭的方向为p3,…,由此经过n次寻找到f(x)的最小值。
也就是说,我们需要找到合适的基{p1,p2,…,pn},从而确定方向、步长的迭代式,满足 ,i∈{1,2,…,n}。
好巧不巧,当时,选择方向
,其中
(常数),步长为
(常数),可以满足上述条件。
当时,就可以使
,i∈{1,2,…,n}成立了。
已知 ,那么
总是成立,i∈{1,2,…,n},j∈{1,2,…,i}(简单来说,i表示当前迭代次数,j表示i次之前的每个迭代次数,显然i≠j)。(正是这个独特的导数和梯度条件,使得共轭梯度法的使用范围有限制!)整理一下就是
。这非常容易凑成共轭关系:

这里仅仅得到了基需要满足的条件(即它们必须具有关于Q共轭的性质)。然而,在迭代过程中,程序需要的是pi+1与pi的关系式,以及λi+1与λi的关系式。所以要根据基的共轭特性,找出方向和步长的迭代式。
根据恒成立等式,尝试构造出一类方向迭代式:
。显然当
时,
=0总是成立。这样就确定下方向迭代式了。
通过恒成立等式可以确定步长迭代式。显然当
时,下式成立:

其中可由
推出。
本来这里就结束了,但是大聪明们发现方向中的
是可以简化的,于是将其简化为
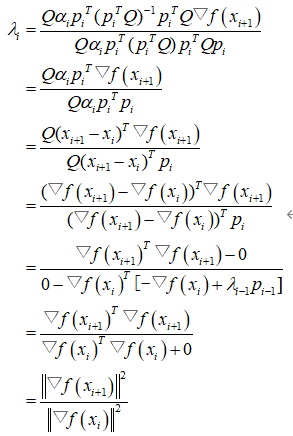
这样方向就可以简单写为 了。嘻嘻。
了。嘻嘻。
4.步骤
首先,找到初始点 。当
梯度不为零时,根据步长和方向的规则

逐次迭代出下一个点 。(若某点梯度为零,那找到极小点咯,就不需要继续迭代咯!)
2021.09.25
注:文中的“显然”只是我猜想大聪明们在构造它们的时候觉得“显然”,我个人觉得一点都不“显然”!