前言
最近在备战软考,复习到数据表示方面相关的知识,所以在这里做一下记录,也方便大家参考。
什么是 R 进制
对于 R 机制,如果要实现与十进制的转换,则使用 按权展开法,其具体操作为:
将
R进制数的每一位数值用 R k R^k Rk 的形式表示,即幂底数为R,指数为k,k与该位和小数点间的间距有关。当该位位于小数点左边时,k则是该位和小数点之间数码的个数;而当该位维语小数点右边时,则k是负值,其绝对值为该位和小数点之间数码的个数加1。
比如二进制和十进制之间的转换: 10111.01 = 1 ∗ 2 4 + 1 ∗ 2 2 + 1 ∗ 2 1 + 1 ∗ 2 0 + 1 ∗ 2 − 2 10111.01 = 1* 2^4+1*2^2+1*2^1+1*2^0+1*2^{-2} 10111.01=1∗24+1∗22+1∗21+1∗20+1∗2−2。
再比如七进制和十进制之间的转换: 403.02 = 4 ∗ 7 2 + 3 ∗ 7 0 + 2 ∗ 7 − 2 403.02 =4*7^2+3*7^0+2*7^{-2} 403.02=4∗72+3∗70+2∗7−2
进制之间的转换
- 十进制转
R进制
使用 短除法,比如我们要将 100 100 100 转换为二进制数,则有如下过程,最终的结果为 1100100 B 1100100B 1100100B。

- 二进制转八/十六进制
假设我们有一个二进制数 100010010011 100010010011 100010010011,如果我们要将其转换为八进制数,一个八进制数需要 8 个基数来表示,所以需要 3 位二进制来表示。那么转换过程如下,即对应的八进制数为 4223 O 4223O 4223O。

而如果我们将要将其转换为十六进制数,一个十六进制数需要 16 个基数来表示,所以需要 4 位二进制来表示。则对应的转换过程如下,即对应的十六进制数为 893 H 893H 893H。
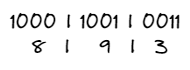
码制
计算机中,无论我们要存储任何数据,它都会转换为二进制码进行存储。现在的计算机中,如果我们要进行加法运算操作,那么我们很容易实现,因为现在的计算机体系大多采用冯诺依曼所提出的经典计算机体系结构,其中就包含了加法运算器。但如果我们要进行减法运算,那么此时就犯难了。没有减法运算器,我们要如何实现减法运算呢?而针对这一问题,原码、反码、补码就产生了。我们常用这三种码来表示一个机器数,从而解决计算机做减法的问题。下面是几个数的实例( 0 0 0 的补码只有一种表现形式),下面就分别来看看几种不同表示法的具体知识。
| 1 | -1 | +0 | -0 | |
|---|---|---|---|---|
| 原码 | 00000001 0000 0001 00000001 | 10000001 10000001 10000001 | 00000000 00000000 00000000 | 10000000 10000000 10000000 |
| 反码 | 00000001 00000001 00000001 | 11111110 11111110 11111110 | 00000000 00000000 00000000 | 11111111 11111111 11111111 |
| 补码 | 00000001 00000001 00000001 | 11111111 11111111 11111111 | 00000000 00000000 00000000 | 00000000 00000000 00000000 |
- 符号位
正式了解不同码制之前,我们先来看看符号位的定义。所谓符号位,是在内存中存放的最左边的一位,如果该位为 0 0 0,那么说明这个数表示的是正数;而假如该位为 1 1 1,那么就说明这个数表示的是负数。
- 原码
是一种最简单的机器数表示法,我们常用最高位来表示符号位,而用余下的其他位来存放该数二进制的绝对值。也即除开符号位之外,原码的数据位就是一个数的二进制绝对值表示。
在上面的示例中,我们发现,虽然 0 0 0 和 − 0 -0 −0 的原码不一致,但是主要还是符号位的不同,我们再用上面的示例来进行运算:
0001 + 0010 = 0011 , 1 + 2 = 3 0001 + 0010=0011,1 + 2 = 3 0001+0010=0011,1+2=3
0000 + 1000 = 1000 , 0 + ( − 0 ) = − 0 0000 + 1000= 1000,0 + (-0)=-0 0000+1000=1000,0+(−0)=−0
0001 + 1001 = 1010 , 1 + ( − 1 ) = − 2 0001+1001=1010,1+(-1)=-2 0001+1001=1010,1+(−1)=−2
可以发现,如果我们只是进行正数之间的加法运算,是不会出现问题的。但一旦出现正负数相加的情况,就会导致错误结果,而这主要是因为符号位所引起。那有没有相应的解决办法呢?别着急,我们接下来去看看反码。
- 反码
虽然原码很简单,但是存在的最大问题在于如果一个数加上其相反数结果不为 0 0 0,即 1 + ( − 1 ) 1 + (-1) 1+(−1) 的结果不为 0 0 0,为了解决这个问题,才有了反码的出现。而针对反码,这里也分为两种情况:
- 如果一个数是正数,那么其反码和原码一样,如 1 1 1 的原码和反码均为 0001 0001 0001。
- 如果一个数是负数,那么其反码就是其原码除符号位之外,按位取反。如 − 1 -1 −1 的原码为 1001 1001 1001,其反码为 1110 1110 1110。
这个时候我们再来看看原码中存在的问题:
0001 + 1001 = 1111 , 1 + ( − 1 ) = − 0 0001+1001=1111,1+(-1)=-0 0001+1001=1111,1+(−1)=−0
可以看到通过使用反码,我们解决了源码中两个相反数之和不为 0 0 0 的情况,但是不是就代表我们可以用反码来进行通用减法运算呢?我们来试试两个不同的负数相加:
1110 + 1100 = 1010 , ( − 1 ) + ( − 3 ) = − 5 1110+1100=1010,(-1)+(-3)=-5 1110+1100=1010,(−1)+(−3)=−5
就离谱,这结果明显错误!所以反码还是不能彻底解决减法运算的问题。而相应的,科学家们又提出了补码这一概念。
- 补码
同样的,补码也很特殊,针对正负数也分为了两种情况:
- 如果一个数是正数,那么该数的补码等于其原码,如 1 1 1 的原码和补码均为 0001 0001 0001。
- 如果一个数是负数,那么该数的补码等于反码
+
1
+1
+1,如
−
1
-1
−1 的反码为
1110,那么其补码即为1111。
同样,我们来试试看反码中进行减法运算所出现错误的情况:
1111 + 1111 = 1110 , ( − 1 ) + ( − 1 ) = − 2 1111+1111=1110,(-1)+(-1)=-2 1111+1111=1110,(−1)+(−1)=−2
诶,完美解决了反码中两个负数相加时所出现的结果错误的情况。因此在计算机中,为了避免运算错误,都是采用的补码进行加减法运算。
- 不同码制之间的转换总结
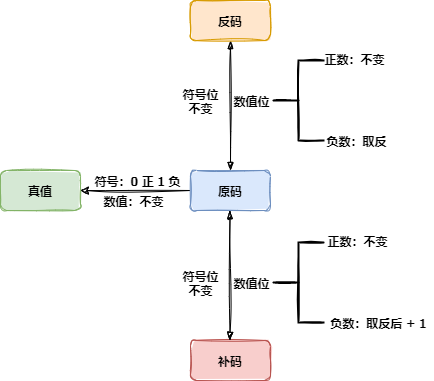
经过上面的各种码制介绍之后,我们将一个数的不同码制之间的转换规律总结如下图:
- 移码
除开常用的原码、反码、补码之外,还有一种码制叫做移码。所谓移码,又叫做增码或者偏置码,它是在数 X X X 上增加一个偏移量来定义的,通常用来表示浮点数的阶码,其表示形式类似于补码,只是其符号位用 1 1 1 来表示正数, 0 0 0 来表示负数,则数值表示部分则是与补码相同。
| 1 | -1 | +0 | -0 | |
|---|---|---|---|---|
| 原码 | 00000001 0000 0001 00000001 | 10000001 10000001 10000001 | 00000000 00000000 00000000 | 10000000 10000000 10000000 |
| 反码 | 00000001 00000001 00000001 | 11111110 11111110 11111110 | 00000000 00000000 00000000 | 11111111 11111111 11111111 |
| 补码 | 00000001 00000001 00000001 | 11111111 11111111 11111111 | 00000000 00000000 00000000 | 00000000 00000000 00000000 |
| 移码 | 10000001 10000001 10000001 | 01111111 01111111 01111111 | 10000000 10000000 10000000 | 00000000 00000000 00000000 |
数值表示范围
在开始了解数值的表示范围之前,我们先来了解下什么叫做定点。所谓定点,是因为小数点的位置是固定的,所以我们叫做数值是定点的整数或者小数。假如一个数值用码制的形式表示, 如果小数点在数值最低位(也即最后边)是,此时该数表示的是定点整数。但如果小数点在介于数值最高位和最低位的中间位置,那么此时该数所表示的就是一个定点小数。
| 码制 | 定点整数 | 定点小数 |
|---|---|---|
| 原码 | − ( 2 n − 1 − 1 ) -(2^{n-1}-1) −(2n−1−1)~ + ( 2 n − 1 − 1 ) +(2^{n-1}-1) +(2n−1−1) | − ( 1 − 2 − ( n − 1 ) ) -(1-2^{-(n-1)}) −(1−2−(n−1))~ + ( 1 − 2 − ( n − 1 ) ) +(1-2^{-(n-1)}) +(1−2−(n−1)) |
| 反码 | − ( 2 n − 1 − 1 ) -(2^{n-1}-1) −(2n−1−1)~ + ( 2 n − 1 − 1 ) +(2^{n-1}-1) +(2n−1−1) | − ( 1 − 2 − ( n − 1 ) ) -(1-2^{-(n-1)}) −(1−2−(n−1))~ + ( 1 − 2 − ( n − 1 ) ) +(1-2^{-(n-1)}) +(1−2−(n−1)) |
| 补码 | − 2 n − 1 -2^{n-1} −2n−1~ + ( 2 n − 1 − 1 ) +(2^{n-1}-1) +(2n−1−1) | − 1 -1 −1~ + ( 1 − 2 − ( n − 1 ) ) +(1-2^{-(n-1)}) +(1−2−(n−1)) |
| 移码 | − 2 n − 1 -2^{n-1} −2n−1~ + ( 2 n − 1 − 1 ) +(2^{n-1}-1) +(2n−1−1) | − 1 -1 −1~ + ( 1 − 2 − ( n − 1 ) ) +(1-2^{-(n-1)}) +(1−2−(n−1)) |
假设我们用 8 个数位来表示一个数值,那么对于定点整数而言,其原码范围就是:
− ( 2 n − 1 − 1 ) -(2^{n-1}-1) −(2n−1−1) ~ + ( 2 n − 1 − 1 ) , − 127 + 127 +(2^{n-1}-1),-127~+127 +(2n−1−1),−127 +127
将其转换为二进制就是: − 11111111 -11111111 −11111111 ~ 01111111 01111111 01111111,那么我们就可以得到该数值补码的范围: 10000000 10000000 10000000 ~ 01111111 01111111 01111111。
同样的,对于定点小数而言,我们用 8 个数位来表示,则其原码范围是:
− ( 1 − 2 − ( n − 1 ) ) -(1-2^{-(n-1)}) −(1−2−(n−1)) ~ + ( 1 − 2 − ( n − 1 ) ) +(1-2^{-(n-1)}) +(1−2−(n−1))
同样将其转换为二进制: − 0.1111111 -0.1111111 −0.1111111 ~ + 0.1111111 +0.1111111 +0.1111111,此时我们就可以得到其对应的补码范围: − 1 -1 −1 ~ + 0.1111111 +0.1111111 +0.1111111。
浮点数的运算
浮点数的表示
所谓浮点数,指的是小数点位置不固定的数,相比整数能够表示更大的范围,其表示格式如下:
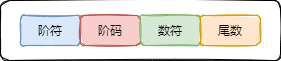
对于一个浮点数 N N N,我们常用如下形式表示:
N = M ∗ R e N = M * R^e N=M∗Re
其中 M M M 叫做 尾数, R R R 叫做 基数,而 e e e 则叫做 指数。其中,指数也叫做阶码,它的位数决定了数值的表示范围,位数越多说明表示的范围越大;而尾数的位数则决定了数值的有效精度,位数越多说明该数的精度越高。
例如对于一个整数 1000 1000 1000,用浮点数的形式表示即为 1000 = 1.0 ∗ 1 0 3 1000 = 1.0 * 10^3 1000=1.0∗103,其中 1.0 1.0 1.0 就对应着浮点数表示形式中的尾数,而 10 10 10 则对应着基数, 3 3 3 则对应着指数。
浮点数运算
既然整数也可以用浮点数的形式表示,那我们就可以把所有的运算都看做是浮点数运算。要进行浮点数运算,我们又该如何进行呢?
我们以一个实例来看看,浮点数之间应该如何进行运算。
假设有如下两个数: m = 1.0 ∗ 1 0 3 m = 1.0*10^3 m=1.0∗103 和 n = 2.5 ∗ 1 0 2 n = 2.5*10^2 n=2.5∗102,要对两个数进行加法运算。
首先,我们发现两个数的指数是不一样的,那要进行加法运算,我们首先将其统一为一个指数,比如统一指数为 2 2 2 或者 3 3 3。按理来讲,任何一个指数都是可以的,但如果我们转换为小的指数( 2 2 2),那么 m = 10.0 ∗ 1 0 2 m = 10.0*10^2 m=10.0∗102,让其与 n n n 进行加法运算得到的结果到时候又需要转换为大的指数( 2 − > 3 2 -> 3 2−>3),此时就显得比较麻烦。所以为了避免结果运算之后再次进行指数的转换,我们 一般推荐统一为大的指数( 3 3 3)。所以我们统一指数之后,得到的两个数分别是:
m = 1.0 ∗ 1 0 3 m = 1.0*10^3 m=1.0∗103
n = 0.25 ∗ 1 0 3 n=0.25*10^3 n=0.25∗103
指数统一之后,我们再来计算尾数,此时尾数则为 1.0 + 0.25 = 1.25 1.0+0.25=1.25 1.0+0.25=1.25。
最后,我们既然得到了尾数、指数和基数,那么对结果进行格式化操作,得到 m + n = 1.25 ∗ 1 0 3 m + n=1.25*10^3 m+n=1.25∗103。注意这里比较特殊,因为我们的结果是很规范的浮点数(即尾数小数点的左边既不能为 0 0 0,也不能是 1 1 1 位以上的数),假设我们的浮点数不是规范的浮点数,那么则需要对其进行格式化操作。
总结起来浮点数的运算过程就是:
对阶 -> 尾数计算 -> 格式化结果
总结
好了,以上就是今天的所有内容了。
主要讲了关于 R 进制的表示,以及如何与十进制进行转换。然后对常见的进制之间的转换做了介绍,接着则是对原码、反码、补码、移码等不同码制之间的转换。最后则是对数值表示范围进行了介绍,以及浮点数运算的相关知识进行补充。
创作不易,如果你觉得我的文章内容对你有所帮助,那就点个赞再走吧!