文章目录
- 《剑指offer》专题—算法训练 day02
- 一、替换空格
- 思路
- 二、从尾到头打印链表
- 思路一
- 思路二
- 思路三
- 三、重建二叉树
- 思路
- 四、斐波那契数列
- 思路一
- 思路二
- 未完待续.....
《剑指offer》专题—算法训练 day02
今天开始了 剑指offer 算法训练的 第二天内容,希望大家可以看看~~
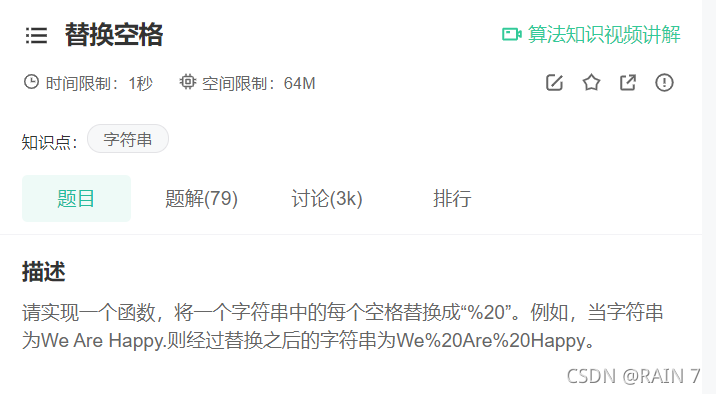
一、替换空格
题目链接:
https://www.nowcoder.com/practice/4060ac7e3e404ad1a894ef3e17650423?
思路
虽然是替换问题,但是生成的字符串整体变长了.
因替换内容比被替换内容长,所以,一定涉及到字符串中字符的移动问题
移动方向一定是向后移动,所以现在的问题无非是移动多少的问题
因为是 ’ ’ -> “%20”,是1换3,所以可以先统计原字符串中空格的个数(设为n),然后可以计算出新字符串的长度
所以:new_length = old_length + 2*n
最后,定义新老索引(或者指针),各自指向新老空间的结尾,然后进行old->new的移动
如果是空格,就连续放入“%20”,其他平移即可。当遇到空格的情况,老指针向前走一格、新指针放一个字符,往前走一格.
题解代码
import java.util.*;
public class Solution {
public String replaceSpace(StringBuffer str) {
// 判断参数的相关情况
if(str == null){
return null;
}
if( str.length() == 0){
return str.toString();
}
// 1.计算这个字符串中 空格存在的个数
int count = 0;
for(int i =0;i<str.length();i++){
if(str.charAt(i) == ' '){
count++;
}
}
int oldLength = str.length();
str.setLength(oldLength + 2*count);
int newLength = str.length();
int index = newLength-1;
for(int i =oldLength-1;i >=0;i--){
if(str.charAt(i) == ' '){
str.setCharAt(index--,'0');
str.setCharAt(index--,'2');
str.setCharAt(index--,'%');
}else{
str.setCharAt(index--,str.charAt(i));
}
}
return str.toString();
}
}
二、从尾到头打印链表
题目链接:
https://www.nowcoder.com/practice/d0267f7f55b3412ba93bd35cfa8e8035?
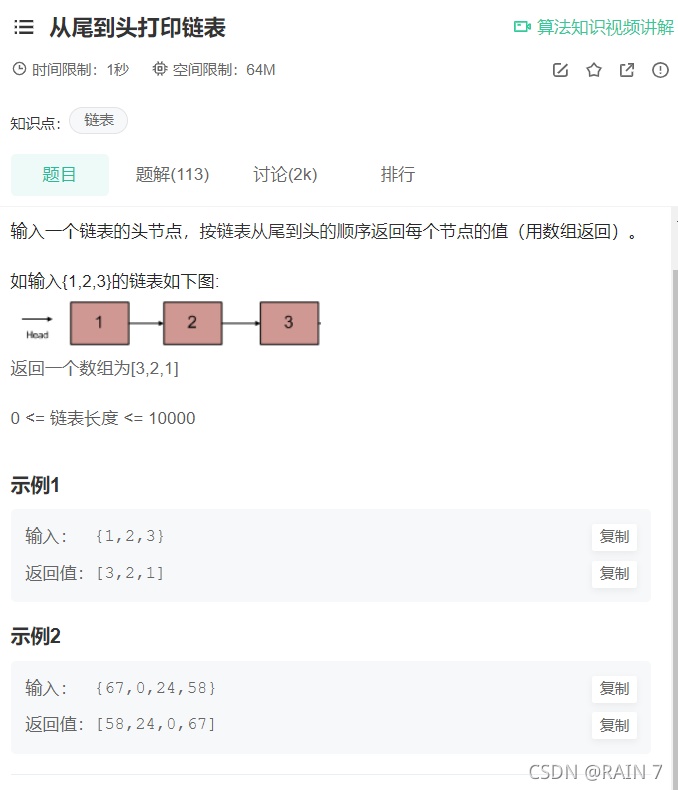
这个题的思路有很多种,个人推荐使用递归的思路
思路一
stack 入栈
我们可以将这个链表的每一个节点的值 都入栈 ,之后出栈时 打印出栈的节点值,最后就得到了我们需要的从尾打印
这里我们运用了栈 的特点: 先进后出,后进先出
相关代码
/**
* public class ListNode {
* int val;
* ListNode next = null;
*
* ListNode(int val) {
* this.val = val;
* }
* }
*
*/
import java.util.*;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
Stack<Integer> stack = new Stack<>();
while(listNode != null){
stack.push(listNode.val);//取当前节点的值入栈
listNode = listNode.next;// 更新当前节点为下一个节点
}
while(!stack.isEmpty()){
list.add(stack.pop()); // 去除当前栈顶元素然后放入 list 当中
}
return list;
}
}
思路二
逆置数组
我们可以先遍历链表,将每个节点的值都存入到 list 当中
然后逆置 list
相关代码
/**
* public class ListNode {
* int val;
* ListNode next = null;
*
* ListNode(int val) {
* this.val = val;
* }
* }
*
*/
import java.util.*;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
// 按顺序将链表中节点的值 放入数组中
while(listNode != null){
list.add(listNode.val);
listNode = listNode.next;
}
Collections.reverse(list);// 我们可以用一个内置的逆置数组函数
// 或者也可以写一个 逆置数组的程序过程,不算太难
return list;
}
}
思路三
递归
/**
* public class ListNode {
* int val;
* ListNode next = null;
*
* ListNode(int val) {
* this.val = val;
* }
* }
*
*/
import java.util.*;
public class Solution {
public void printListFromTailToHeadHelper(ArrayList<Integer>list,ListNode listNode){
if(listNode == null){
return;
}
printListFromTailToHeadHelper(list,listNode.next);
list.add(listNode.val);
}
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
printListFromTailToHeadHelper(list,listNode);
return list;
}
}
递归思路的代码可能在 牛客网过不去,可能数据量给的有点大,造成了栈溢出,但是总体上思路是对的.
三、重建二叉树
题目链接:
https://www.nowcoder.com/practice/8a19cbe657394eeaac2f6ea9b0f6fcf6?

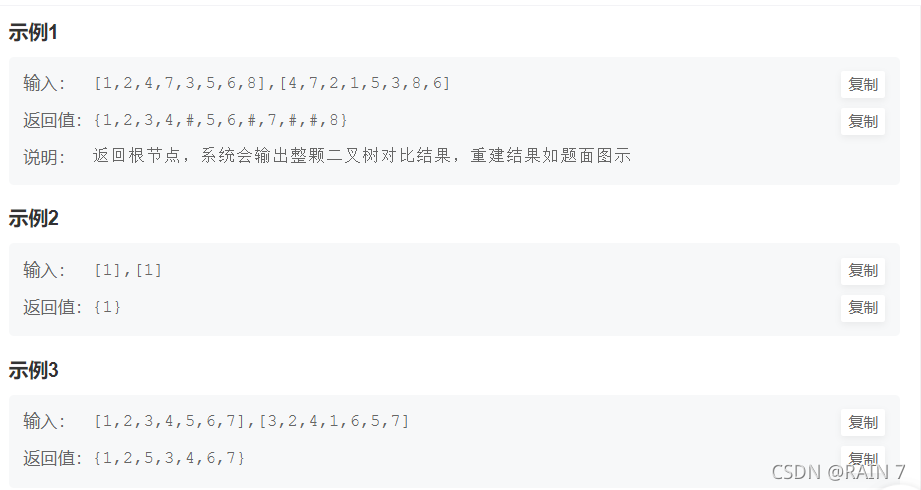
思路
利用递归
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.*;
public class Solution {
// 将重建二叉树问题 化解成 递归的问题 ,每颗子树都可被视为一个新的二叉树
public TreeNode reConstructBinaryTreeHelper(int[] pre,int pre_start,int pre_end,int[] vin,int vin_start,int vin_end){
// 递归的终止条件
if(pre_start>pre_end || vin_start>vin_end){
return null;
}
TreeNode root = new TreeNode(pre[pre_start]);// 先定义一个根节点
// 遍历中序数组,找到 pre[pre_start] 这个数字
for(int i = 0;i<vin.length;i++){
// 此时i对应的就是每棵树的根节点
// 中序遍历中 i左边的是 左树 , i右边的是 右树
if(vin[i] == pre[pre_start]){
// 这里找到根节点之后,在利用递归找到每颗子树的左右子树.条件很重要(记得写准确)
root.left = reConstructBinaryTreeHelper(pre,pre_start+1,pre_start+i-vin_start,vin,vin_start,i-1);
// pre_start 是根节点,pre_start+1 到 pre_start+ ((i-1)-vin_start)这是 左树在 先序遍历中的区间(闭区间)
// vin_start 到 i-1 这是在 左树在中序遍历中的区间(闭区间)
root.right = reConstructBinaryTreeHelper(pre,pre_start+i-vin_start+1,pre_end,vin,i+1,vin_end);
// pre_start+ ((i-1)-vin_start) +1 到 pre_end 这是 右树在前序遍历中的区间
// i+1,vin_end 这是 右树在中序遍历中的区间
break;
}
}
// 返回根节点
return root;
}
public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
if(pre == null || vin == null || pre.length!=vin.length){
return null;
}
return reConstructBinaryTreeHelper(pre,0,pre.length-1,vin,0,vin.length-1);
}
}
四、斐波那契数列
相信很多人已经了解了什么是斐波那契数列,这也是一道相对简单的题目,但是这道题的重点却不是解题,而是 了解剪枝操作,并且引入动态规划的思想.

思路一
迭代的思路是相对简单的,定义 三个数字,来回 迭代…
相关代码
import java.util.*;
// 斐波那契数列 1 1 2 3 5 8 13
public class Solution {
public int Fibonacci(int n) {
int first = 1;
int second = 1;
int third = 0;
if(n == 1){
return 1;
}
if(n==2){
return 1;
}
while(n>2){
third = first + second;
first = second;
second = third;
n--;
}
return third;
}
}
思路二
递归 或者说 是 动态规划,递归的过程会涉及到很多重复计算,造成计算量过于复杂,所以我们要进行 剪枝操作
未剪枝的递归代码
import java.util.*;
// 斐波那契数列 1 1 2 3 5 8 13
public class Solution {
public int Fibonacci(int n) {
if(n==0){
return 0;
}
if(n<=2){
return 1;
}
// 根据斐波那契数列的规律 我们可以得到这样的公式 F(n)=F(n-1)+F(n-2)
return Fibonacci(n-1)+Fibonacci(n-2);
}
}
我们用递归写出了斐波那契数列的相关代码,但是这就涉及到一个效率问题了
我们来看一下 斐波那契数列的 递归计算过程
例如我们当 n== 7 时 函数在递归是对同一个 f(n) 进行了多次计算,大大浪费了效率
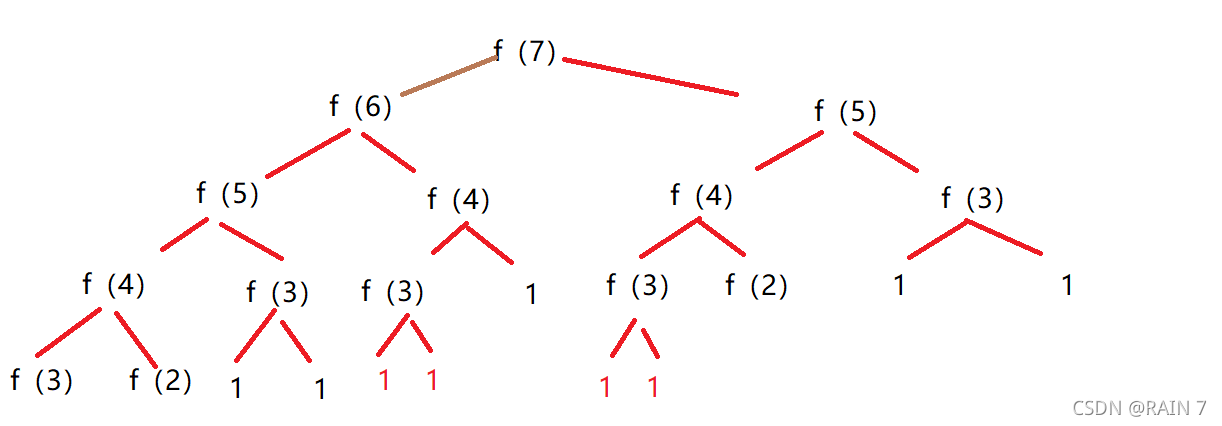
我们希望这个递归函数 对于 已经计算过的 f(n) ,可以使用以前计算过的结果来进行运算
在这里,我们就要用到 map 集合来进行相关的剪枝操作
斐波那契数列在实际处理的时候,其实就是作为一个二叉树进行处理的,以上图为例,如果我们可以把 f(3) 的结果保存一下,那么在之后 涉及到 f(3) 的计算就可以用保存过的数据进行替代,就不用在进行递归了,所以这样就大大降低了 计算的效率.
相关代码
import java.util.*;
// 斐波那契数列 1 1 2 3 5 8 13
public class Solution {
Map<Integer,Integer> map = new HashMap<>();
// 这个map 一定要在 函数外面实例化,否则每次递归都要实例化一次,时间复杂度太大
public int Fibonacci(int n) {
if(n == 0 || n ==1){
return n;
}
// 根据斐波那契数列的规律 我们可以得到这样的公式 F(n)=F(n-1)+F(n-2)
if(n == 2){
return 1;
}
// 定义一个 f(n-2) , 在 map 中查找一下是否存有这个结果 ,如果没有递归计算然后保存在 map,如果有那么ppre 等于map中存的哪个值
int ppre = 0;
if(map.get(n-2) != null){
// 在map 中找到 f(n-2)
ppre = map.get(n-2);
}else{
// 在 map 当中 没有找到 f(n-2)
// 那么我们只能够进行递归计算,然后别忘记 计算结果放入 map 当中
ppre = Fibonacci(n-2);
map.put(n-2,ppre);
}
int pre = 0;
if(map.get(n-1)!= null){
// 在 map 当中找到f(n-1)
pre = map.get(n-1);
}else{
// 在map 当中 没有找到 f(n-1)
// 那么我们只能够进行递归计算,然后别忘记,计算结果放入到 map 当中
pre = Fibonacci(n-1);
map.put(n-1,pre);
}
// 这里大家要思考一下,我在保存 pre 和 ppre 这两个数字的时侯,为社么要先保存ppre
// 因为如果 我在 map 当中先保存了 f(n-2) 的话,那么我们在计算 f(n-1) 的时候效率又提高了.
return pre+ ppre;
}
}
好了,今天的内容就结束了,希望大家多多练习~~
谢谢欣赏!!!
《剑指offer》 算法训练day2 敬请期待…