题目链接: 674. 超级2048 - AcWing题库
题目描述:
2048 是一个著名的单人游戏,其目标是在网格上滑动图块以组合它们并创建数字为2048的图块。
2048 在一个简单的4×4 网格上进行游戏,其中有一些图块,玩家可以对它们进行移动。
每一步操作,玩家可以选择向左,向右,向上和向下 4 个方向去移动所有图块。
如果两个包含数字相同的图块在移动时发生碰撞,则它们将合并为一个图块,该图块上的数值为两个图块的数字之和。
在一次操作中,一个新创建的图块不能再次参与合并,并且图块们总是优先沿着移动方向与其旁边的图块进行合并。
例如,如果三个 2 在一行构成 2 2 2,这时玩家选择向左移动,则它将变为 4 2 0,最左边的两个 22 会被合并。
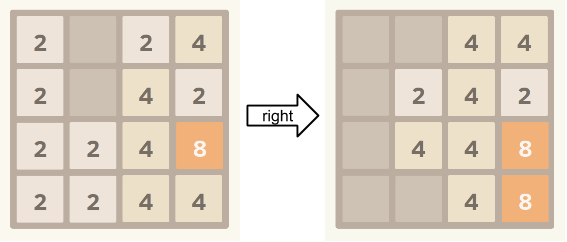
上图显示了当玩家将所有图块“右移”时 4×4 网格的变化情况。
爱丽丝和鲍勃非常喜爱这个游戏。
但是几轮后,他们觉得网格的尺寸太小了并不刺激,所以决定将网格的尺寸扩大到 N×NN×N,他们称之为“超级 2048”游戏。
但是难度的激增让他们无法驾驭这个游戏。
他们要求你编写一个程序来帮助他们弄清楚在所有图块沿着某个特定方向移动后网格的样子。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 N 和一个字符串 DIR,其中 NN 表示网格的尺寸,DIR 表示图块的移动方向,DIR 将会是以下四个字符串中的一个:left, right, up, down。
接下来 N 行,每行包含 N 个整数,用来描述网格的初始状态,每个整数表示网格中一个图块的值,如果为 0 则表示该位置是空的。
输出格式
对于每组测试数据,第一行输出 Case #x:,其中 x 为组别编号(从 1 开始)。
然后输出 N 行,每行 N 个空格隔开的整数,表示图块移动后网格的样子。
数据范围
1≤T≤100
1≤N≤20
网格中的每个数字都是 0 或 2 到 1024 之间的 2 的整数次幂,包括 2 和 1024。
输入样例:
3
4 right
2 0 2 4
2 0 4 2
2 2 4 8
2 2 4 4
10 up
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
3 right
2 2 2
4 4 4
8 8 8
输出样例:
Case #1:
0 0 4 4
0 2 4 2
0 4 4 8
0 0 4 8
Case #2:
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
Case #3:
0 2 4
0 4 8
0 8 16思想
(此距离为右向移动,图片丑请勿怪):
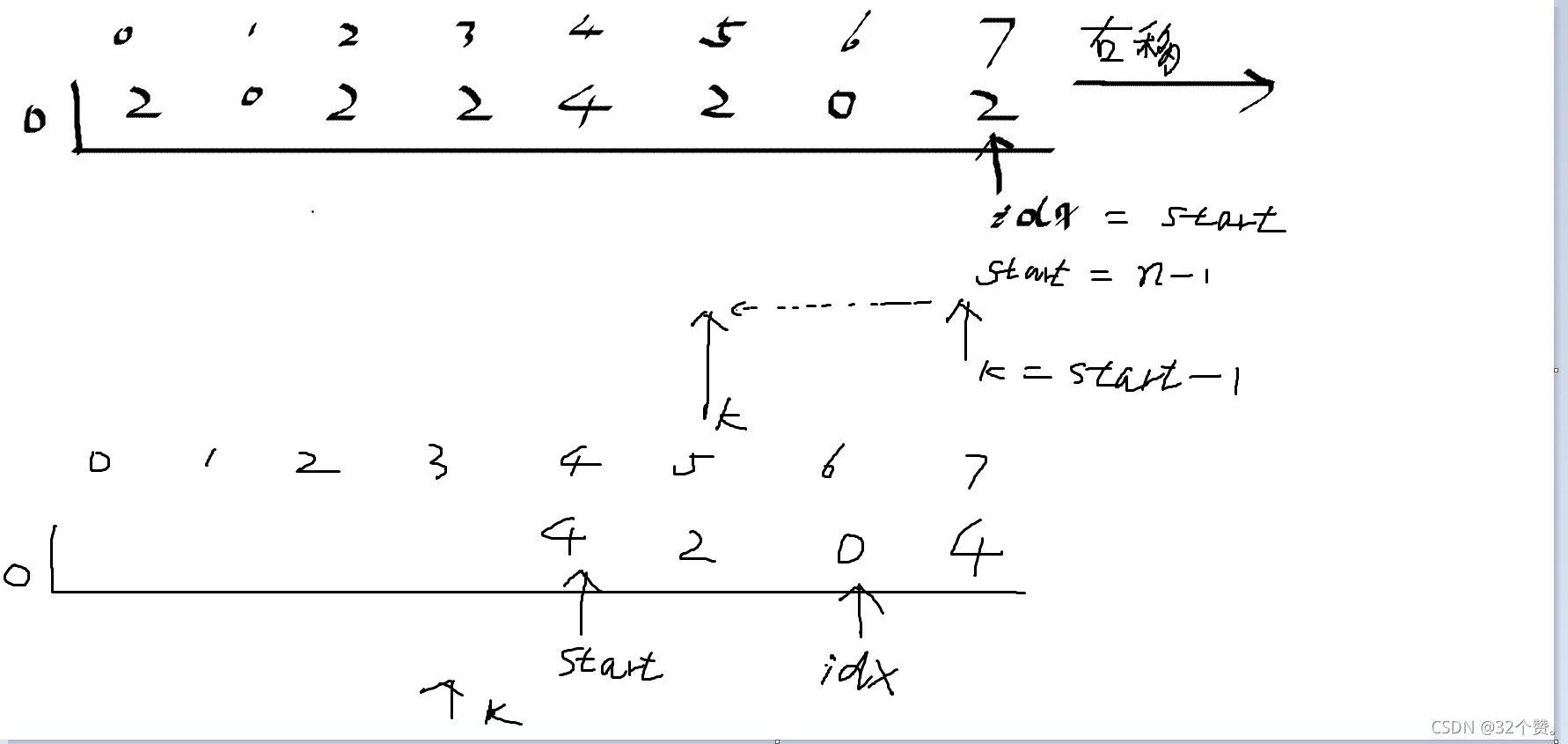
定义start下标指针,指向遍历的起点,idx初始值为遍历的开始起点也就是start的初始值
由start开始遍历,由新的 k 下标指针(start - 1),进行遍历到start当前位置之后(此“之后为遍历的下一个位置的意思),当遇到不为0的时候停止。查看当前 k 和 start指向值的关系,如果是相同的那么也就发生了“碰撞”行为(2048游戏中移动时相邻的相同值会被合并,以下我简称”碰撞“),那么将 idx 指向的下标位置的值赋值为 当前 start 值指向的两倍、如果没有发生”碰撞“,那么将 idx 指向的下标位置的值赋值为 当前 start 值,随后,将 start 的下标位置挪动到当前 k 下标所指向的位置。此图为第一次遍历之后所产生的情况。
当最后一次遍历之后会是下图的情况
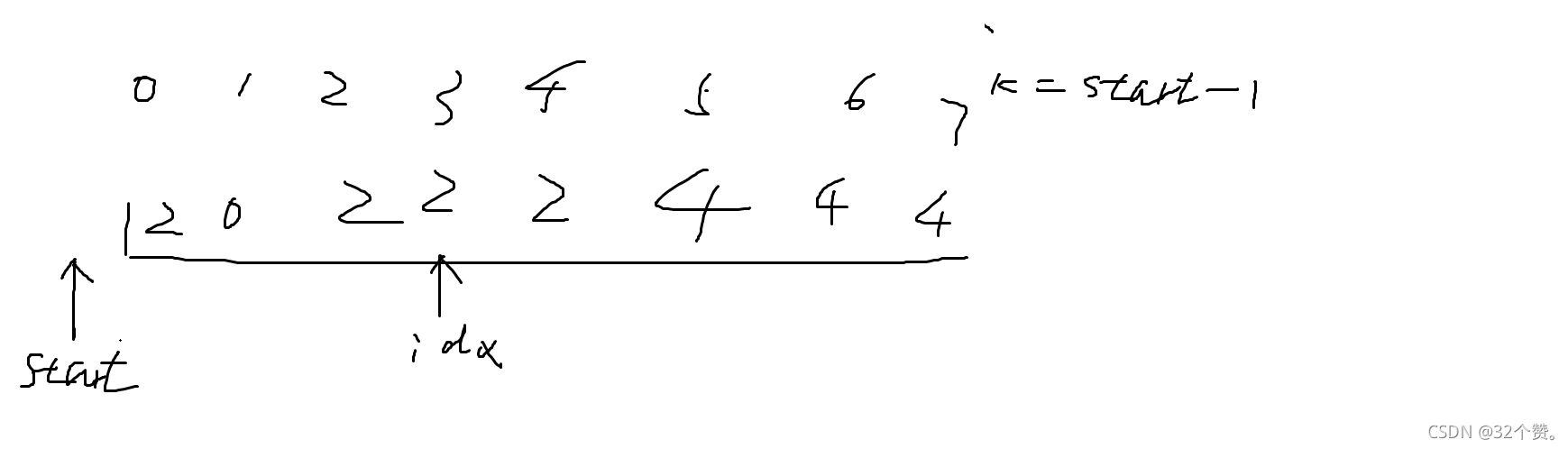
完成之后,在以idx为遍历起点,将之后的值初始化为‘空’(0值),即可
先是最为初始化的思想,将上下左右的移动,写出为四个函数:
之后将是把四个情况融合在一起:
#include <bits/stdc++.h>
using namespace std;
const int N = 30;
int arr[N][N];
void getUp(int n);
void getDown(int n);
void getLeft(int n);
void getRight(int n);
int main() {
int t;cin >> t;
for (int t1 = 1;t1 <= t;t1 ++) {
int n;
string str;
cin >> n >> str;
for (int i = 0;i < n;i ++)
for (int j = 0;j < n;j ++) cin >> arr[i][j];
if (str == "up") getUp(n);
if (str == "down") getDown(n);
if (str == "left") getLeft(n);
if (str == "right") getRight(n);
cout << "Case #" << t1 << ":" << endl;
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) cout << arr[i][j] << ' ';
cout << endl;
}
}
return 0;
}
void getUp(int n){
for (int i = 0;i < n;i ++) { // 遍历每一列
int idx = 0;
for (int j = 0;j < n;j ++) {
if (arr[j][i] == 0) continue; // j => 行号
if (j + 1 >= n) {
arr[idx ++][i] = arr[j][i];
continue;
}
int k = j + 1;
while (k < n && arr[k][i] == 0) k ++;
if (k < n && arr[j][i] == arr[k][i]) {
arr[idx ++][i] = 2 * arr[j][i];
j = k;
}
else arr[idx ++][i] = arr[j][i];
}
for (int j = idx;j < n;j ++) arr[j][i] = 0;
}
}
void getDown(int n){
for (int i = 0;i < n;i ++) { // 遍历每一列
int idx = n - 1;
for (int j = n - 1;j >= 0;j --) {
if (arr[j][i] == 0) continue; // j => 行号
if (j - 1 < 0) {
arr[idx --][i] = arr[j][i];
continue;
}
int k = j - 1;
while (k >= 0 && arr[k][i] == 0) k --;
if (k >= 0 && arr[j][i] == arr[k][i]) {
arr[idx --][i] = 2 * arr[j][i];
j = k;
}
else arr[idx --][i] = arr[j][i];
}
for (int j = idx;j >= 0;j --) arr[j][i] = 0;
}
}
void getLeft(int n){
for (int i = 0;i < n;i ++) {
int idx = 0;
for (int j = 0;j < n;j ++) {
if (arr[i][j] == 0) continue;
if (j + 1 >= n) {
arr[i][idx ++] = arr[i][j];
continue;
}
int k = j + 1;
while (k < n && arr[i][k] == 0) k ++;
if (k < n && arr[i][j] == arr[i][k]) {
arr[i][idx ++] = 2 * arr[i][k];
j = k;
}
else arr[i][idx ++] = arr[i][j];
}
for (int j = idx;j < n;j ++) arr[i][j] = 0;
}
}
void getRight(int n){
for (int i = 0;i < n;i ++) {
int idx = n - 1;
for (int j = idx;j >= 0;j --) {
if (arr[i][j] == 0) continue;
if (j - 1 < 0) {
arr[i][idx --] = arr[i][j];
continue;
}
int k = j - 1;
while (k >= 0 && arr[i][k] == 0) k --;
if (k >= 0 && arr[i][j] == arr[i][k]) {
arr[i][idx --] = 2 * arr[i][k];
j = k;
}
else arr[i][idx --] = arr[i][j];
}
for (int j = idx;j >= 0;j --) arr[i][j] = 0;
}
}
将四种情况写到了一种函数当中:
#include <bits/stdc++.h>
using namespace std;
const int N = 30;
int arr[N][N];
void check(int n, int fleft, int fright);
int main() {
int t;cin >> t;
for (int t1 = 1;t1 <= t;t1 ++) {
int n;string str;
cin >> n >> str;
for (int i = 0;i < n;i ++)
for (int j = 0;j < n;j ++) cin >> arr[i][j];
if (str == "up") check(n, 0, 1);
if (str == "down") check(n, 0, -1);
if (str == "left") check(n, 1, 0);
if (str == "right") check(n, -1, 0);
cout << "Case #" << t1 << ":" << endl;
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) cout << arr[i][j] << ' ';
cout << endl;
}
}
return 0;
}
/* 解决2048游戏中横竖向移动问题, 其中arr是存储为int类型的2048图
@parma n 当前移动位置的长度, 默认区间在[0, n-1]中
@parma frow 当前是否横向移动, frow > 0 => 向右移动, frow < 0 => 向左移动, frow == 0 不移动
@parma fcol 当前是否纵向移动, fcol > 0 => 向上移动, fcol < 0 => 向下移动, fcol == 0 不移动
*/
void check(int n, int frow, int fcol) {
// 判断当前是否出现了不移动,或者横纵向同时移动的状态,此为错误的操作
if ((frow == 0 && fcol == 0) || (frow != 0 && fcol != 0)) return;
int start, flag; // 定义开始遍历的起点下标, 遍历的方向
// 当flag = 1时候,即为从左往右(从上往下)开始遍历, 为-1的时候就相反
// ----------------相应的start起点下标也就是0,----------------n - 1
if (frow > 0 || fcol > 0) start = 0, flag = 1;
else start = n - 1, flag = -1;
for (int i = 0;i < n;i ++) { // 开始横线或纵向遍历
//定义一个和start同向且初始值相同的下标指针,当2048开始移动时发生碰撞产生改变时
//存储点的下标位置
int idx = start;
//开始纵向或横线遍历,这取决外层循环的涵义
for (int j = start;j >= 0 && j < n;j += flag) {
//当frow != 0,表示现在外层循环是一个纵向遍历,内层循环是一个横向遍历…………
//即在遍历过程中遇到0,也就是2048游戏中的空位的时候,进行一个跳过
if ((frow != 0 && arr[i][j] == 0) || (fcol != 0 && arr[j][i] == 0)) continue;
//如果在遍历过程中出现了遍历到最后一个的情况下,那么需要进行特殊处理
if ((flag > 0 && j + 1 >= n) || (flag < 0 && j - 1 < 0)) {
//判断是横向移动还是纵向移动,进行移动赋值
frow == 0 ? arr[idx][i] = arr[j][i] : arr[i][idx] = arr[i][j];
idx += flag;// 存储点的更新 row86
continue;
}
//定义k指针为当前j指针的后一个(此前并非为j + 1,而是遍历元素的后一个,与遍历方向有关
int k = j + flag;
//用于跳过j指针后存在的'空'(0值),直到找到相同值或不同值
if (fcol != 0) while (k >= 0 && k < n && arr[k][i] == 0) k += flag;//纵向遍历
else while (k >= 0 && k < n && arr[i][k] == 0) k += flag;//横向遍历
//找到需要处理的值之后,判断横纵向遍历
if (frow == 0) {
//如果当前 k 指针没有越界行为,并且与 j 指针指向的值相同,即发生碰撞
if (k >= 0 && k < n && arr[j][i] == arr[k][i])
arr[idx][i] = 2 * arr[j][i], j = k;
else arr[idx][i] = arr[j][i];// 有不同值则赋值到存储点
}
else {
if (k >= 0 && k < n && arr[i][j] == arr[i][k])
arr[i][idx] = 2 * arr[i][j], j = k;
else arr[i][idx] = arr[i][j];
}
//处理完一次碰撞或没有碰撞之后,存储点的位置也要跟随start遍历的方向挪动
idx += flag;
}
//移动处理完之后,剩余的部分理应为'空'(0值)
for (int j = idx;j >= 0 && j < n;j += flag)
//判断横纵向遍历,进行赋值
frow == 0 ? arr[j][i] = 0 : arr[i][j] = 0;
}
}