1.堆的概念
堆通常是一个可以被看做一棵完全二叉树。
(1)大根堆, 就是说这个完全二叉树中每一棵子树的根节点都大于他的左右孩子(如果有的话)。
(2)小根堆,就是说这个完全二叉树中每一棵子树的根节点都小于他的左右孩子(如果有的话)。
在数组中:
如果父节点的下标为i,则左孩子的下标为 2 * i + 1,右孩子下标为2*i+2。
如果孩子的下标为j, 则父节点的下标是:( j - 1 ) / 2。
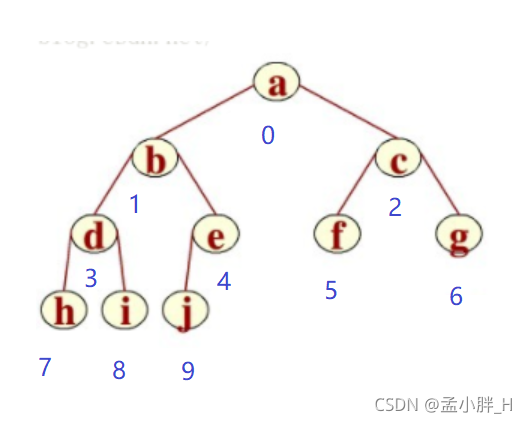
2.堆的调整建立过程
将数组中的数据调整成堆时,从最后一棵子树开始,向根节点一颗颗调整,每棵子树的调整都是从其根节点开始向下调整的。
先用i指向子树的根节点,j为根节点的左孩子。将i位置的值保存到tmp中, 然后在左右孩子中找到较大的哪一个,j指向较大值,(1)如果较大的哪一个比临时变量中的值小,则直接退出;(2)如果较大的哪一个比临时变量中的值大,则将较大的值保存到i位置上,然后i=j,j=2*i+1,直到j越界则退出。退出以后,还需要将tmp的值保存到退出时的i位置上。
我们以数组7,3,2,4,3,11,57,23,1,3,4为例
它们根据下标对应的树形关系如下:
调整是以底向上的调整。第一次调整就是最后一颗子树,如下红圈即最后一棵子树,以下标集合表示,{4,9,10}即最后一颗子树
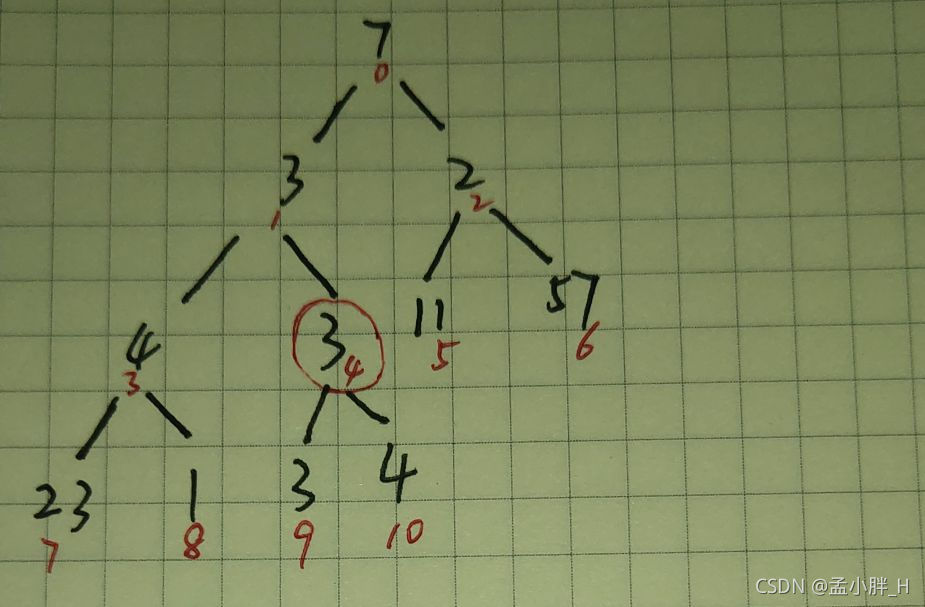
调整后变成如下的一颗树,{3,7,8}是倒数第二颗子树,对其进行调整,使得根(下标3)值最大
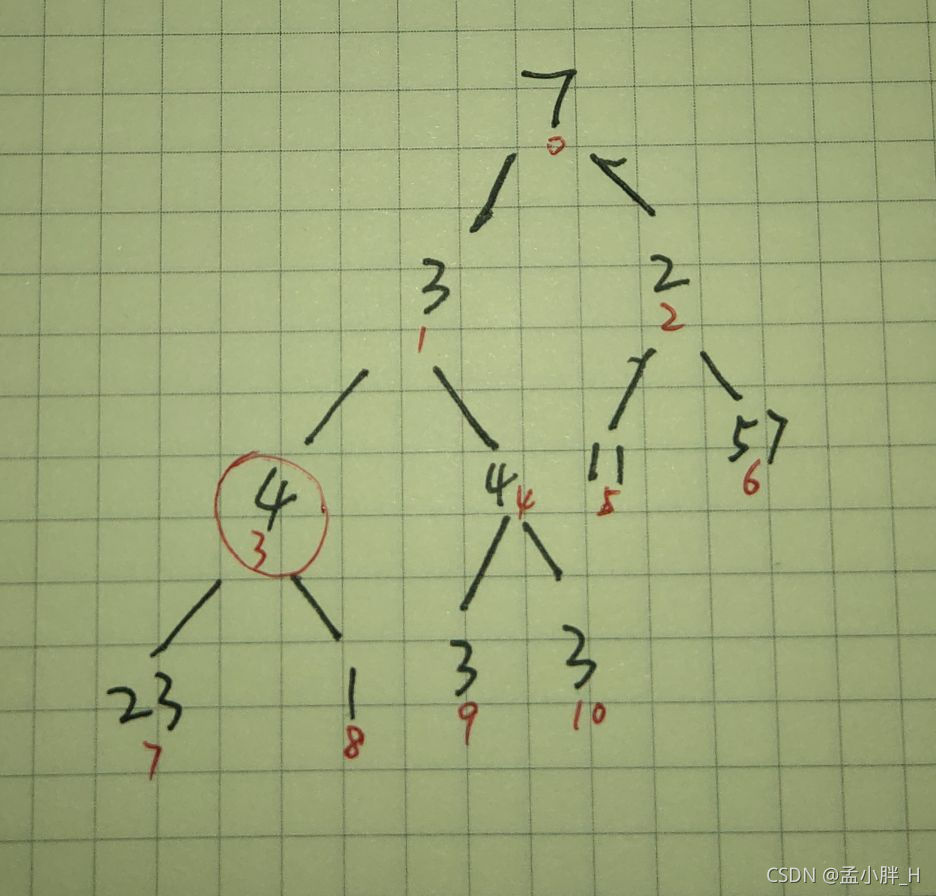
调整后变成如下一棵树,{2,5,6}即我们要调整的下一颗树,使得这颗子树的最大值放在根上(即下标2上)。
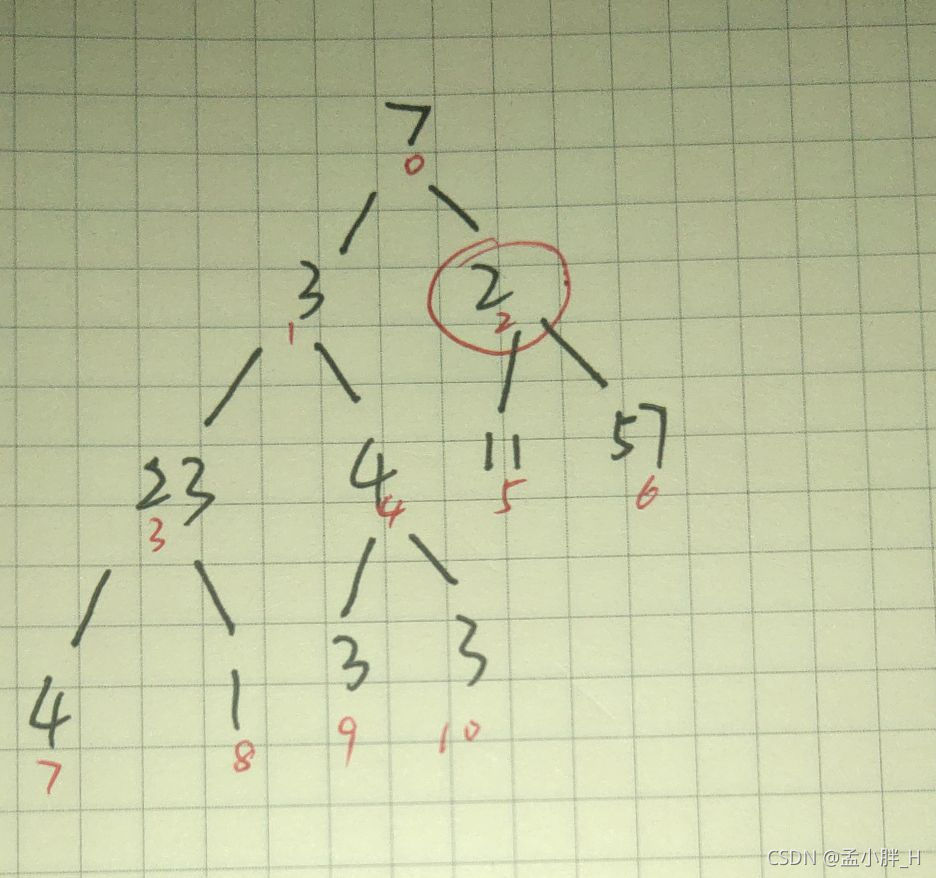
调整后如下树。
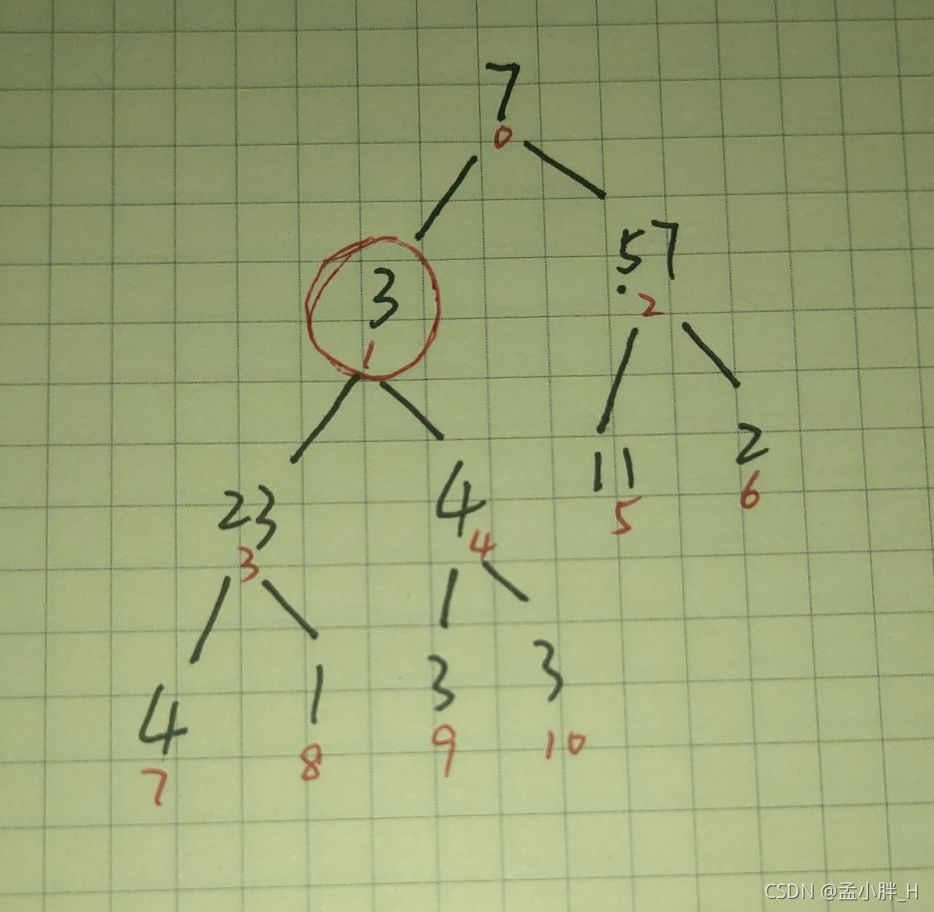
下一颗要调整的树是{1,3,4,7,8,9,10},在这里要注意一下,我们需要对每一颗子树的所有根进行调整,即先调整下标为1的这个根,然后调整下标为3或者4的其中一个根,比如这棵子树,i是下标1,j是下标为3和4中的值较大的一个下标,在这里j就是下标3,由于sum[i] < sum[j]所以将下标i和j的值交换,变成如下图的树:
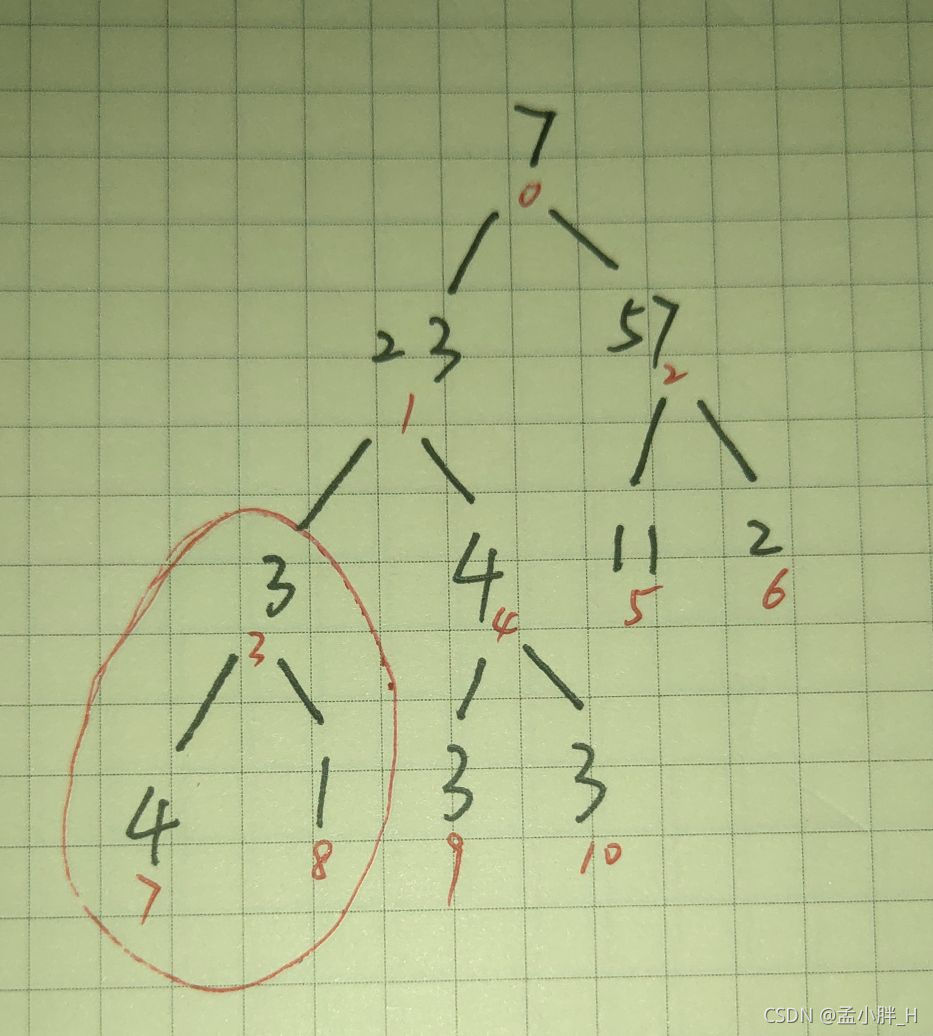
由于子树{3,7,8}根值变动了,所以我们需要对子树{3,7,8}再次进行调整。调整后如下图:

然后再对树{0,1,2,3,4,5,6,7,8,9,10}进行调整,和上次调整一样,在这里我们需要让下标0,1,2中最大值放在0下标即被调整的树的根的位置,在这里我们就把57(下标2)和7(下标0)交换了。
然后再对树{2,5,6}进行调整,直至调整到最后一个根节点,调整完后的树为:
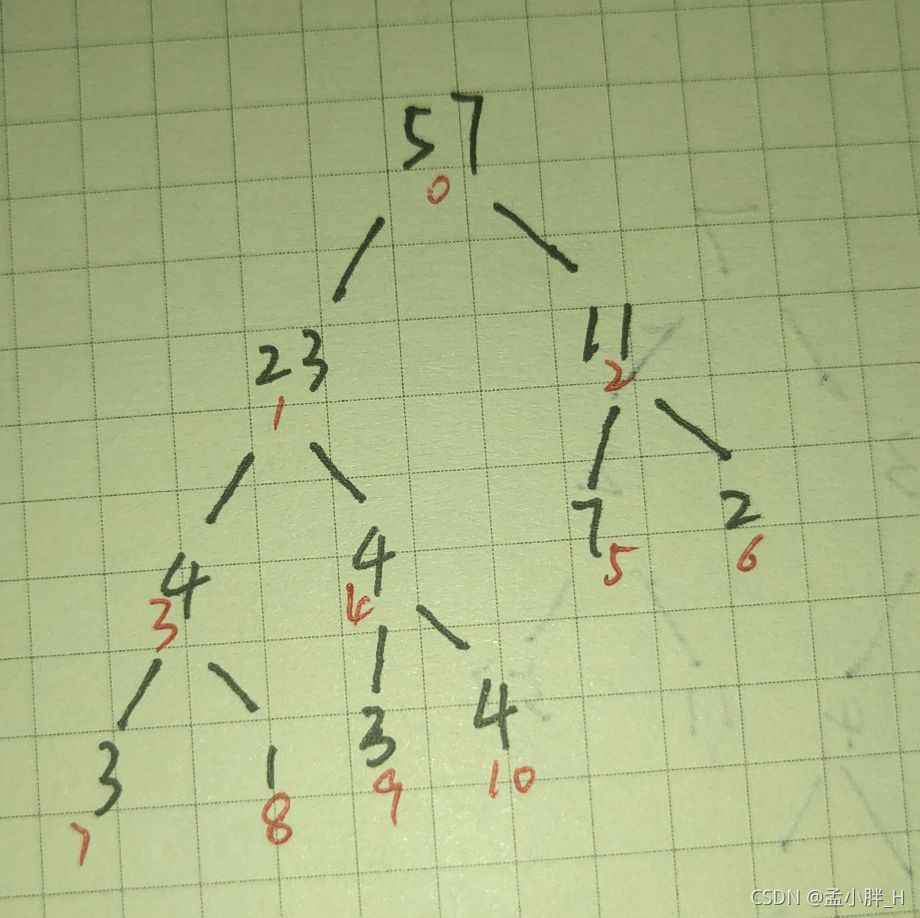
注意这棵树是我们进行两次交换后的结果,即下标0和下标2,下标2和下标5,如果下标5是个根节点的话(即下标5有子节点),那么我们需要对以下标5为根节点的树继续进行调整,直至调整到叶子节点或者子树已经是大根堆为止。
下面代码是对一棵树的调整代码(注意被调整前的树的左右两颗子树肯定是大根堆),那么怎么保证被调整的树的子树是大根堆呢?我们只需要从一颗大树的最后一个根节点一个一个根节点向root结点开始调整就可以。就是我们上面的调整过程。
#include<iostream>
#include<assert.h>
using namespace std;
void OneAdjust(int* arr, int len, int root)
{
int i = root;
int j = 2 * i + 1;
while (j < len)
{
if (j + 1 < len && arr[j] < arr[j + 1])//让j是左右子结点值较大的下标
{
j = j + 1;
}
if (arr[i] >= arr[j])//说明需要调整的树的根节点比左右子节点都大,左右子树都是大根堆,所以这棵树也是大根堆
{
break;
}
else//
{
swap(arr[i], arr[j]);
i = j;//调整改动的子树
j = 2 * i + 1;
}
}
}
我们需要从最后一个根,慢慢向上面的根调整,所以整棵树的调整代码如下:
void CreateHeap(int* arr,int len)
{
int lastroot = (len - 1 - 1) / 2;//找最后一棵子树的根节点下标,len-1是最后一个节点的下标,再-1然后除以2就是最后一个根
for (int i = lastroot; i >= 0; i--)//从lastroot,向上一个根一个根的调整
{
OneAdjust(arr, len, i);
}
}
3.堆排
先将数组中的数据调整成一棵最大堆, 然后将根节点的数据和最后位置的节点交换(即调整一次,将大根堆的根放在最后), 接着除过最后一个位置的数据外,在将剩余的数据调整成最大堆。
重复上述过程,直到只剩下一个数据没有交换。就完成了堆排序。
// 时间复杂度: O(nlog(n))
// 空间复杂度: O(1)
// 稳定性: 不稳定
void HeapSort(int* arr, int len)
{
CreateHeap(arr, len);
for (int i = 0; i < len - 1; i++)
{
swap(arr[0], arr[len - 1 - i]);//将大根堆的根值放在待排序数据的最后位置
OneAdjust(arr, len-1-i, 0);//只需要对剩下的数据进行一次调整,对根进行调整
}
}
int main()
{
int arr[] = { 1,3,4,7,8,23,51,67,3,0 };
HeapSort(arr, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
运行结果: