目录

一、线性回归

<1>线性回归中的函数

<2>线性回归方程绘图

​

二、多项式回归

三、拟合度输出

四、线性预测 

五、多元回归

---

一、线性回归

<1>线性回归中的函数

stats.mode()            #众数
numpy.median()          #中位数
numpy.mean()            #平均数
numpy.std()             #标准差
numpy.var()	      #方差
numpy.percentile(数组，数字) 
x = numpy.random.uniform(0.0,5.0,250)
 #250 个介于 0 到 5 之间的随机浮点数的数组
 x = numpy.random.normal(5.0, 1.0, 100000) 
 #正态随机数组 平均值为 5.0，标准差为 1.0

标准差 sigma σ

方差 sigma square σ^2

百分位数：

假设我们有一个数组，包含住在一条街上的人的年龄。

ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

什么是 75 百分位数？答案是 43，这意味着 75％ 的人是 43 岁或以下

<2>线性回归方程绘图

import matplotlib.pyplot as plt
from scipy import stats

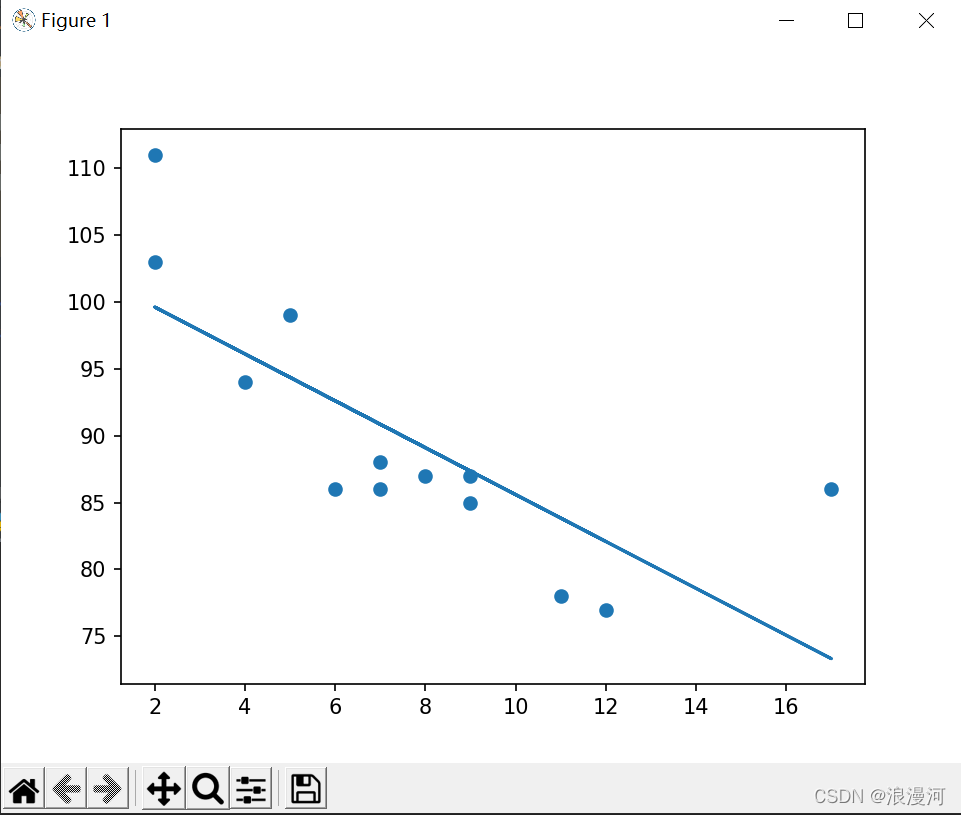
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)
#slope 是线性回归线的 斜率，  intercept 是 线性回归线的截距， r 是衡量拟合性能度量(越高拟合越好（0-1）)

def myfunc(x):
  return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

运行结果 

二、多项式回归

import numpy
import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

myline = numpy.linspace(1, 22, 100)

plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()

运行结果

1、np.poly1d()此函数有两个参数：

　　参数1：为一个数组，若没有参数2，则生成一个多项式，例如：

　　　　　　p = np.poly1d([2,3,5,7])   

　　　　　　print(p)    ==>>2x3 + 3x2 + 5x + 7    数组中的数值为coefficient（系数），从后往前 0，1，2.。。为位置书的次数

       参数2：若参数2为True，则表示把数组中的值作为根，然后反推多项式，例如：

　　　　　　q = np.poly1d([2,3,5],True)

　　　　　　print(q)   ===>>(x - 2)*(x - 3)*(x - 5)  = x3 - 10x2 + 31x -30

　　参数3：variable=‘z’表示改变未知数的字母，例如：

　　　　　　q = np.poly1d([2,3,5],True,varibale = 'z')

　　　　　　print(q)   ===>>(z - 2)*(z - 3)*(z - 5)  = z3 - 10z2 + 31z -30

三、拟合度输出

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

print(r2_score(y, mymodel(x)))

运行结果

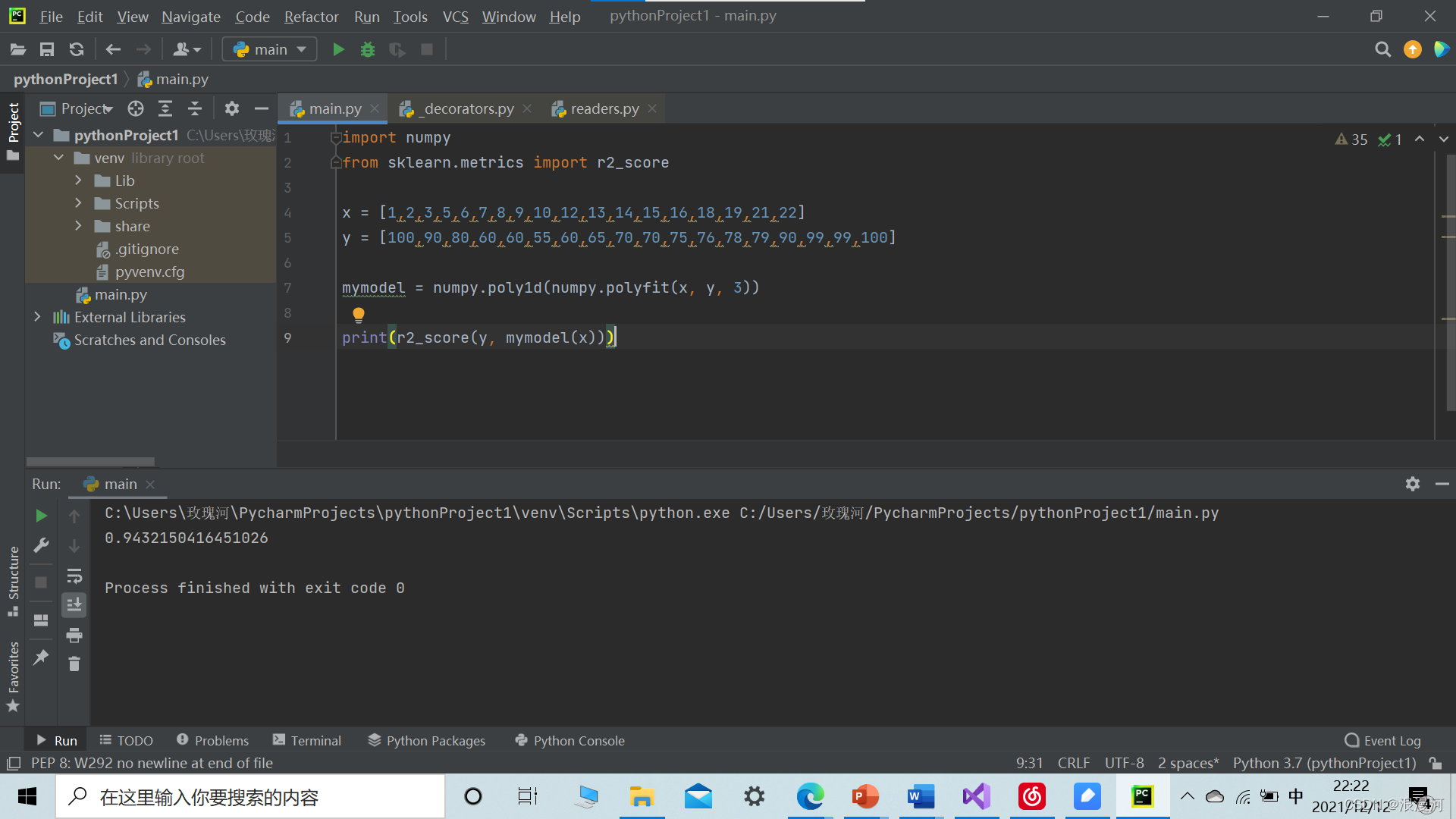
 r=0.9432150416451026 拟合度很好

四、线性预测 

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

speed = mymodel(17)
print(speed)

运行结果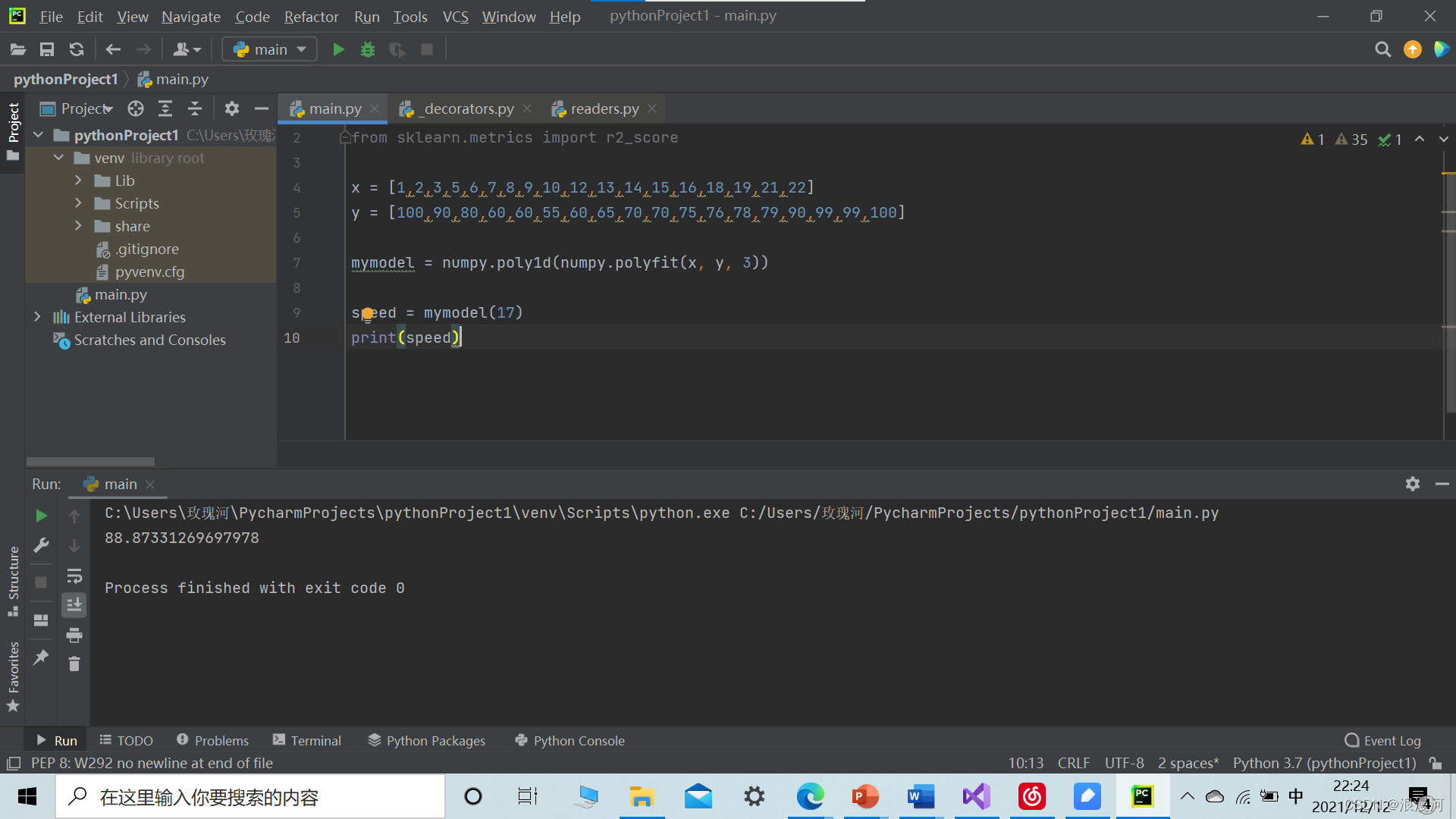

 可以得到当x=17时，y=88.87331269697978

五、多元回归

多元回归就像线性回归一样，但是具有多个独立值，这意味着我们试图基于两个或多个变量来预测一个值。

可以通过以下数据，经过分析得到线性回归方程从而预测结果。

Car	Model	Volume	Weight	CO2
Toyota	Aygo	1000	790	99
Mitsubishi	Space Star	1200	1160	95
Skoda	Citigo	1000	929	95
Fiat	500	900	865	90
Mini	Cooper	1500	1140	105
VW	Up!	1000	929	105
Skoda	Fabia	1400	1109	90
Mercedes	A-Class	1500	1365	92
Ford	Fiesta	1500	1112	98
Audi	A1	1600	1150	99
Hyundai	I20	1100	980	99
Suzuki	Swift	1300	990	101
Ford	Fiesta	1000	1112	99
Honda	Civic	1600	1252	94
Hundai	I30	1600	1326	97
Opel	Astra	1600	1330	97
BMW	1	1600	1365	99
Mazda	3	2200	1280	104
Skoda	Rapid	1600	1119	104
Ford	Focus	2000	1328	105
Ford	Mondeo	1600	1584	94
Opel	Insignia	2000	1428	99
Mercedes	C-Class	2100	1365	99
Skoda	Octavia	1600	1415	99
Volvo	S60	2000	1415	99
Mercedes	CLA	1500	1465	102
Audi	A4	2000	1490	104
Audi	A6	2000	1725	114
Volvo	V70	1600	1523	109
BMW	5	2000	1705	114
Mercedes	E-Class	2100	1605	115
Volvo	XC70	2000	1746	117
Ford	B-Max	1600	1235	104
BMW	2	1600	1390	108
Opel	Zafira	1600	1405	109
Mercedes	SLK	2500	1395	120

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量：

predictedCO2 = regr.predict([[2300, 1300]])

print(predictedCO2)

Pandas 模块允许我们读取 文件并返回一个 DataFrame 对象。（可以用外部的excel表的数据）

使用LinearRegression()函数创建线性回归对象。