☘前言☘

今天是九日集训第三天，我会记录一下学习内容和题解，争当课代表0.0.
注意！！！！题解的解法1是今天要掌握的解法，解法2是学有余力再研究，涉及到后面知识点0.0
链接：《LeetCode零基础指南》(第四讲) 一维数组

🧑🏻作者简介：一个从工业设计改行学嵌入式的年轻人
✨联系方式：2201891280(QQ)
⏳全文大约阅读时间： 20min

---

---

🎁主要知识点梳理

📝数组相关定义

🚗1.顺序存储

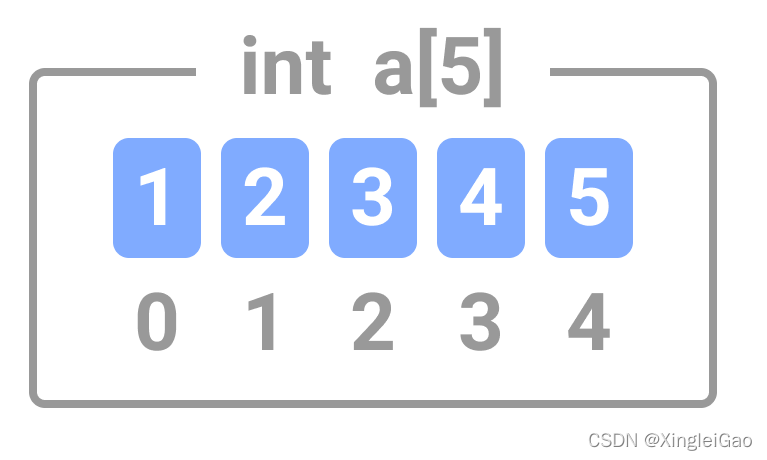
顺序存储结构，是指利用一段连续的存储单元来存储元素。如下图，每一块都对应了一个数组元素。

🚕2.定义和初始化

一个数组的定义为:

int a[10];

对应于字符串或者浮点数就是char str[10];、double db[10];

---

一维数字的初始化为

int a[5] = { 1, 2, 3, 4, 5,};

如果只需要初始化部分的数据我们可以不去计算有几个元素。如下：

int a[] = {1, 2, 3, 4, 5};

如果我们只需要初始化一部分值就可以如下声明初始化：

int a[10] = {1, 2, 3, 4, 5};

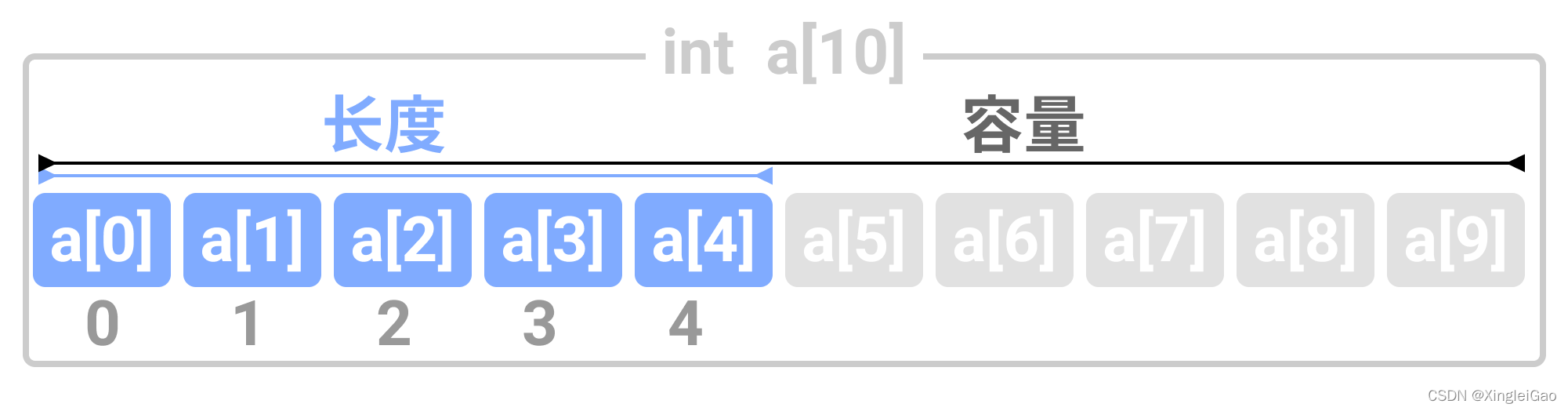
🚌3.长度和容量

• 数组的长度是当前一共有多少元素。
• 数组的容量是指声明的数组的长度。

比如上面的只初始化一部分的容量就如图

🚓4.数组元素调用

我们可以用[]运算符来索引对应的元素

int a[10] = {1, 2, 3, 4, 5};
int a = a[4];
int b = a[8];
int c = a[10];//errot

一定要注意我的图上数组是从0号开始的，所以int a[10]后绝对没有a[10]元素，访问越界。

🚑5.数组的参数传递

一般只传递数组的首地址，也就是下面这种形式。

int add(int *nums, int numsSize) {
   // ...
}

其中的int *nums和int nums[]是等价写法，同时，a[5]和*(a+5)也是等价写法！

---

🍗课后习题

33. 搜索旋转排序数组

33. 搜索旋转排序数组
题目描述

整数数组nums按升序排列，数组中的值 互不相同 。
在传递给函数之前，nums 在预先未知的某个下标k（0 <= k < nums.length）上进行了 旋转，使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如，[0,1,2,4,5,6,7]在下标 3 处经旋转后可能变为[4,5,6,7,0,1,2]。
给你 旋转后 的数组 nums 和一个整数target ，如果 nums 中存在这个目标值target，则返回它的下标，否则返回 -1。

思路

从前到后搜，搜的到就是有，搜不到就是没有！

int search(int* nums, int numsSize, int target){
    for(int i = 0; i < numsSize; ++i)
        if(target == nums[i]) return i;
    return -1;
}

---

81. 搜索旋转排序数组 II

81. 搜索旋转排序数组 II
题目描述

整数数组nums按升序排列，数组中的值 互不相同 。
在传递给函数之前，nums 在预先未知的某个下标k（0 <= k < nums.length）上进行了 旋转，使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如，[0,1,2,4,5,6,7]在下标 3 处经旋转后可能变为[4,5,6,7,0,1,2]。
给你 旋转后 的数组 nums 和一个整数target ，如果 nums 中存在这个目标值target，则返回它的下标，否则返回 -1。

思路

和上面那道题是一样的。

int search(int* nums, int numsSize, int target){
    for(int i = 0; i < numsSize; ++i)
        if(target == nums[i]) return i;
    return -1;
}

---

153. 寻找旋转排序数组中的最小值

153. 寻找旋转排序数组中的最小值
题目描述

已知一个长度为n的数组，预先按照升序排列，经由1到n次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7]在变化后可能得到：

• 若旋转 4次，则可以得到[4,5,6,7,0,1,2]
• 若旋转7次，则可以得到[0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]]。
给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。

思路

哦，上次找元素，这次找最小值，那就一个一个比较呗？

int findMin(int* nums, int numsSize){
    int ans = 50000;//定义到最大值
    for(int i = 0;i < numsSize;i++)
        if(ans >nums[i]) ans = nums[i];
    return ans;
}

---

70. 爬楼梯

70. 爬楼梯
题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

思路

这和数组有什么关系呢？
其实是一道动态规划问题，但是也不难。理解一下
到达第i个台阶是不是有两种方式？

• 一种是从第i－2阶蹦上来。
• 一种是从第i阶蹦上来
  这就是传说中的状态转移。我们初始化第一阶和第二阶方法，其他的按照上面说的生成就好了。

int climbStairs(int n){
    if(!n)  return 0;
    else if(n == 1) return 1;
    else if(n == 2) return 2;//直接返回
    int ans[n];
    ans[0] = 1;//初始化为第一阶的方法数
    ans[1] = 2;//初始化为第二阶的方法数
    for(int i = 2;i<n;i++)
        ans[i] = ans[i-1]+ans[i-2];//从前到后生成
    return ans[n-1];//返回第n阶的方法数
}

---

509. 斐波那契数

509. 斐波那契数
题目描述

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给你n，请计算F(n)。

思路

这个昨天写过，思路确实是用到数组保存求过的值。然后从前往后求就好啦0.0

int Fib[31];
int fib(int n){
    Fib[0] = 0;
    Fib[1] = 1;
    for(int i = 2;i <= n;i++)
        Fib[i] = Fib[i-1] + Fib[i-2];
    return Fib[n];
}

---

1137. 第 N 个泰波那契数

1137. 第 N 个泰波那契数
题目描述

泰波那契序列 Tn 定义如下：
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

思路

和上面的思路非常类似，直接看代码吧0.0

int a[38];
int tribonacci(int n){
    a[0] = 0;a[1] = 1;a[2] = 1;
    for(int i =3;i <= n;i++ )
        a[i] = a[i-1] + a[i-2] + a[i-3];
    return a[n];
}

---

2006. 差的绝对值为 K 的数对数目

2006. 差的绝对值为 K 的数对数目
题目描述

给你一个整数数组 nums 和一个整数 k ，请你返回数对 (i, j) 的数目，满足 i < j 且 |nums[i] - nums[j]| == k 。
|x| 的值定义为：

• 如果 x >= 0 ，那么值为 x 。
• 如果 x < 0 ，那么值为 -x 。

思路

因为只要求数量，不要求具体的哪个数，所以可以先排序
主要的思路

• 从小到大排序
• 利用快慢指针来寻找满足条件的两个值。
• 找到后ans+=对应的成立数量。
  注释：high-a是high满足条件的值。temp是满足上一次算的满足条件的值，如果这次low的值和上次的一样，直接加就好了。

int a[38];
int tribonacci(int n){
    a[0] = 0;a[1] = 1;a[2] = 1;
    for(int i =3;i <= n;i++ )
        a[i] = a[i-1] + a[i-2] + a[i-3];
    return a[n];
}int cmp(int *a,int *b){return *a > *b;}
int countKDifference(int* nums, int numsSize, int k){
    int ans = 0,temp = 0;
    qsort(nums,numsSize,sizeof(int),cmp);
    int low = 0,high = 0;
    while(high < numsSize || (low && low <numsSize && nums[low] == nums[low - 1])){
        while(high < numsSize && nums[high] - nums[low] < k ) high++;
        int a = high;//第一个可能成立的点
        while(high < numsSize && nums[high] - nums[low] == k)  high++;//第一个不成立的点
        if(low && nums[low] == nums[low - 1])    ans+=temp;//与上次的low相同直接加就好了
        else ans+=high - a,temp = high - a;
        low ++;
    }
    return ans;
}

---

LCP 01. 猜数字

LCP 01. 猜数字
题目描述

小A 和 小B 在玩猜数字。小B 每次从 1, 2, 3 中随机选择一个，小A 每次也从 1, 2, 3 中选择一个猜。他们一共进行三次这个游戏，请返回 小A 猜对了几次？
输入的guess数组为 小A 每次的猜测，answer数组为 小B 每次的选择。guess和answer的长度都等于3。

思路

这意思就是数组1和数组2对应元素相等就统计一次呗？

int game(int* guess, int guessSize, int* answer, int answerSize){
    int ans = 0;
    for(int i = 0;i < guessSize;i++)
        if(guess[i] == answer[i])   ans++;
    return ans;
}

---

LCP 06. 拿硬币

LCP 06. 拿硬币
题目描述

桌上有n堆力扣币，每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆，拿走其中的一枚或者两枚，求拿完所有力扣币的最少次数

思路

看起来花里胡哨，翻译一下就是每一个数如果是偶数就/2，奇数就+1/2最终和是多少？这不是就简单了对不对？

int minCount(int* coins, int coinsSize){
    int ans = 0;
    for(int i = 0;i < coinsSize;i++)
        ans += coins[i] & 1 ? ((coins[i]+1)/2) : coins[i]/2;
    return ans;
}

---

📑写在最后

今天完成了第三天的打卡，今天的算法笔记记录刚好也是一维数组，你说巧不巧，哈哈哈，我真不是故意的，但是真的推荐读一读，万字长文，请给出一定的时间。《算法笔记知识点记录》第二章——快速入门2[选择结构、循环结构和数组]