
前言:
我们之前似乎确凿在C语言教学里讲过堆,但是那是操作系统中的堆,我们今天将要讲的堆是数据结构里的堆。数据结构中也有栈和堆,它跟操作系统对内存划分中的栈和堆没有关系。我横竖卷不动其他人,于是就打算再更亿篇博客罢。
 (一开口就老周树人了)
(一开口就老周树人了)
一、堆的概念与性质
0x00 堆的概念
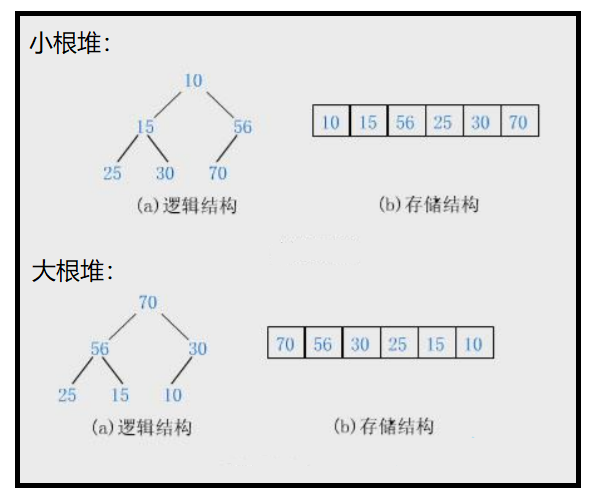
【百度百科】堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
📚 若有一个关键码的集合 , 堆分为大堆和小堆。将其所有元素按完全二叉树的顺序存储在一个数组中:
① 如满足 且
则称为小堆。
② 如满足 且
,则称为大堆。
我们将根节点最大的堆称作最大堆(即大根堆),根节点最小的堆称作最小堆(即小根堆)。
🔺 综上所述:
① 大堆:树中任何一棵树及子树中,父亲的值都大于等于孩子 ( )
② 小堆:树中任何一颗树及子树中,父亲的值都小于等于孩子 ( )
0x01 堆的性质
① 堆总是一棵完全二叉树。
② 堆中的某个节点的值总是不大于或不小于其父节点的值。
0x02 堆的作用
① 堆排序
② 解决 问题,在
个数中找出最大的前
个或找出最小的
个
……
二、堆的定义
所有的数组都可以表示成完全二叉树,但是它不一定是堆。大堆:树中所有父亲都大于等于孩子小堆:树中所有父亲都小于等于孩子。下面我们将要实现的是大堆。
0x00 数组堆
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //指向动态开辟的数组
int size; //有效数据的个数
int capacity; //容量空间的大小
} HP;
0x01 接口函数
📚 这是需要实现几个接口函数:
/* 堆的初始化 */
void HeapInit(HP* php);
/* 堆的销毁 */
void HeapDestroy(HP* php);
/* 堆的打印 */
void HeapPrint(HP* php);
/* 判断堆是否为空 */
bool HeapIfEmpty(HP* hp);
/* 堆的插入 */
void HeapPush(HP* php, HPDataType x);
/* 检查容量 */
void HeapCheckCapacity(HP* php);
/* 交换函数 */
void Swap(HPDataType* px, HPDataType* py);
/* 大根堆上调 */
void BigAdjustUp(int* arr, int child);
/* 小根堆上调 */
void SmallAdjustUp(int* arr, int child);
/* 堆的删除 */
void HeapPop(HP* php);
/* 小根堆下调*/
void SmallAdjustDown(int* arr, int n, int parent);
/* 大根堆下调 */
void BigAdjustDown(int* arr, int n, int parent);
/* 返回堆顶数据*/
HPDataType HeapTop(HP* php);
/* 统计堆的个数 */
int HeapSize(HP* php);
三、堆的实现
先前在讲解实现顺序表的时候详细说过了,都是老生常谈的陈芝麻烂谷子了,这里部分接口的解析就不再详细解读了,如果记不得了建议再复习一下之前讲的顺序表。
🔗 链接:【数据结构】顺序表详解
0x00 堆的初始化(HeapInit)
💬 Heap.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //指向动态开辟的数组
int size; //有效数据的个数
int capacity; //容量空间的大小
} HP;🔑 解读:堆的实际结构就是一个数组,我们用数组去实现,想要让它支持增删查改,我们就不能使用静态数组,要用动态数组。这样我们就可以扩容,有 size 和 capacity,这里和顺序表差不多,这是一个非常通用的结构。
💬 Heap.c
/* 堆初始化 */
void HeapInit(HP* php) {
assert(php);
php->array = NULL;
php->capacity = php->size = 0;
}
0x01 堆的销毁(HeapDestroy)
💬 Heap.h
void HeapDestroy(HP* php);💬 Heap.c
/* 堆的销毁 */
void HeapDestroy(HP* php) {
assert(php);
free(php->array);
php->capacity = php->size = 0;
}
0x02 堆的打印(HeapPrint)
💬 Heap.h
void HeapPrint(HP* php);💬 Heap.c
/* 堆的打印 */
void HeapPrint(HP* php) {
int i = 0;
for (i = 0; i < php->size; i++) {
printf("%d ", php->array[i]);
}
printf("\n");
}
0x03 判断堆是否为空(HeapEmpty)
💬 Heap.h
/* 判断堆是否为空 */
bool HeapIfEmpty(HP* hp);
💬 Heap.c
/* 判断堆是否为空 */
bool HeapIfEmpty(HP* php) {
assert(php);
return php->size == 0; // 如果为size为0则表示堆为空
}🔑 解读:这里巧妙利用布尔特性,直接 return 数组大小即可。 size == 0 则为真,反之返回假。
0x04 大堆的插入(HeapInit)
📌 插入的核心思路:

① 先将元素插入到堆的末尾,即最后一个孩子之后。
② 插入之后如果堆的性质遭到破坏,就将新插入的节点顺着其的父亲往上调整到合适位置。直到调到符合堆的性质为止。
我们先来解决这个插入功能,先实现下增容部分的代码,方便我们下面能更专心地研究堆的插入问题。这个我们在顺序表里也详细讲过,这里我们再复习一下:
检查是否需要增容(HeapCheckCapacity)
void HeapCheckCapacity(HP* php) {
if(php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : (php->capacity * 2); //第一次给4,其他情况扩2倍
HPDataType* tmpArray = (HPDataType*)realloc(php->array, sizeof(HPDataType) * newCapacity); // 数组扩容
if(tmpArray == NULL) { //检查realloc
printf("realloc failed!\n");
exit(EXIT_FAILURE);
}
//更新他们的大小
php->array = tmpArray;
php->capacity = newCapacity;
}
}🔑 解读:参考顺序表章节的讲解,这里不再赘述。
根据堆的性质,如果不满足大堆和小堆,出现子大于父或父大于子的情况,为了保证插入之后堆还是堆,我们就需要进行自下往上的调整。堆插入数据对其他节点没有影响,只是可能会影响从它到根节点路径上节点的关系。
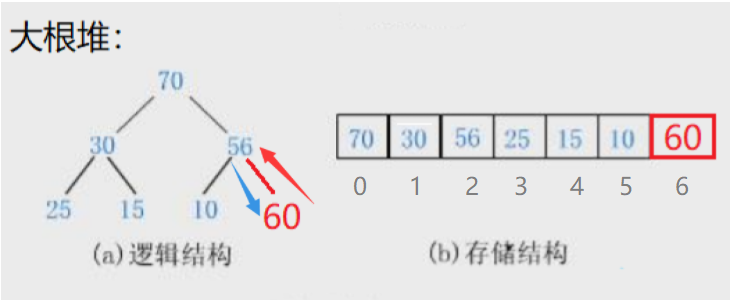
💭 举例:
① 比如下面的情况:新插入的为 60,子大于父(60 > 56 ),这时就需要交换。
② 还有更特殊的情况:比如新插入的为 100,100 和 56 交换完之后还要和 70 交换。
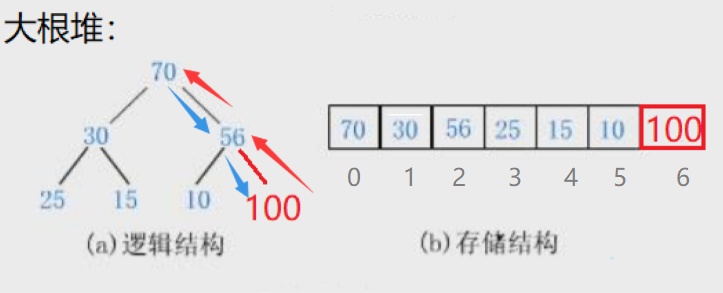
先把父亲赋值给孩子,再把孩子赋值给父亲,再让父亲往上走,判断是否比父亲大,如果大就再进行交换。 为了搞定这些情况,我们就需要写一个 "向上调整" 的算法(最坏调到根停止):
向上调整(AdjustUp)
void AdjustUp(int* arr, int child) {
assert(arr);
// 首先根据公式计算算出父亲的下标
int parent = (child - 1) / 2;
// 最坏情况:调到根,child=parent 当child为根节点时结束(根节点永远是0)
while(child > 0) {
if(arr[child] > arr[parent]) { // 如果孩子大于父亲(不符合堆的性质)
// 交换他们的值
HPDataType tmp = arr[child];
arr[child] = arr[parent];
arr[parent] = tmp;
// 往上走
child = parent;
parent = (child - 1) / 2;
} else { // 如果孩子小于父亲(符合堆的性质)
// 跳出循环
break;
}
}
}🔑 解读:
① 设计 AdjustUp 接口时需要先想好要接收什么值,因为我们想要对数组内容进行调整,所以我们需要传入数组,并用 int* 接收。另外用 child 接收我们刚插入的值的下标,作为调整位置的起始位置。
② 首先要防止传入的数组为空。
③ 我们首先要确定孩子和父亲的下标,已知孩子求父亲:
(该公式在上一章已经学过了)
孩子下标我们已经有了,因为我们把调整位置的起始位置,也就是刚插入的数据传到了该函数中并以 child 接收了。这时我们定义 parent 变量,根据公式就可以推导出父亲的下标了。
④ 我们已经得到了孩子和父亲的下标,我们就可以开始进行操作了。首先分析一下最坏的情况,最坏的情况就是调到根位置,child = parent,因为根节点永远是 0,child 为 0 时那么 parent 就该小于 0 了,所以当 child 作为根节点时就说明已经调完了,这里我们 while 的判断条件为 child > 0,至于为什么这里要这么别扭地以 child > 0 作为条件而不是 parent >= 0,我们下面会细说。
⑤ 进入循环后先 if 判断,如果数组中 child 的值大于 parent 的值,说明孩子大于父亲,这意味着不符合大堆的性质。我们就要进行置换的操作。这里我们创建一个 HPDataType 类型的 tmp 临时变量进行交换即可。
⑥ 交换完毕后,他们的值已经互相交换好了,这时我们要改变 parent 和 child 的指向,让它们继续往上走,以便于继续进行判断。child = parent,parent 再次根据公式算出新的 parent 即可。
⑦ 设计下 if 的 else 部分,如果数组的 child 的值大于 parent 的值,说明符合大堆的性质了, break 跳出循环即可。
❓ 写循环条件时为什么要写成:while(child > 0) 我们要看是否调到根了,按照正常思路,不应该是看 parent 是否小于0吗? while(parent >= 0)
💡 这么写是不行的!这么写实际上是存在问题的我们带入一个值看看就知道了:
while(child > 0) ✅
while(parent >= 0) ❌
我们来分析一下过程,拿个值带入测试一下:假设插入75
【开始】
70
50 30 (p)
25 15 10 75* (c)
parent最后等于2
【第一次】
70 (p)
50 75* (c)
25 15 10 30
parent最后等于0
【最后一次】
(p)
75* (c)
50 70
25 15 10 30
parent最后还是等于0(我们希望它的结果是小于0的)
为什么呢?最后一次往上走时,
child = parent; 此时child=0
parent = (child - 1) / 2;
(0 - 1) / 2 = 0 这么一来parent仍然会是0
导致parent根本就不会小于0!int main(void) {
int parent = (0 - 1) / 2;
printf("%d", parent);
return 0;
}🚩 运行结果: 0
🔺 所以我们要使用 while(child > 0) ,既不会带来问题效果也和 parent>=0 一样。因为当 child = 0 时就说明已经触及到根了。
⚡ 这里我们用到了交换,因为后面写删除接口也是需要用到交换的,我们不妨把它封装成一个接口,方便我们后续可以多次调用:
交换(Swap)
void Swap(HPDataType* px, HPDataType* py) {
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}void AdjustUp(int* arr, int child) {
assert(arr);
// 首先根据公式计算算出父亲的下标
int parent = (child - 1) / 2;
// 最坏情况:调到根,child=parent 当child为根节点时结束(根节点永远是0)
while(child > 0) {
if(arr[child] > arr[parent]) { // 如果孩子大于父亲(不符合堆的性质)
// 交换他们的值
Swap(&arr[child],&arr[parent]); // 传地址
// 往上走
child = parent;
parent = (child - 1) / 2;
} else { // 如果孩子小于父亲(符合堆的性质)
// 跳出循环
break;
}
}
}
检查是否扩容和向上调整的接口都已经写好了,我们现在可以实现堆的插入了:
💬 Heap.h
void HeapPush(HP* php, HPDataType x);💬 Heap.c
void HeapPush(HP* php, HPDataType x) {
assert(php);
// 检查是否需要扩容
HeapCheckCapacity(php);
// 插入数据
php->array[php->size] = x;
php->size++;
// 向上调整 [目标数组,刚插入的数据]
AdjustUp(php->array, php->size - 1);
}🔑 解读:
① 首先检查 php 是否为空。
② 检查是否需要扩容调用我们刚才实现好的 HeapCheckCapacity 接口即可。
③ 随后插入数据即可,这里和顺序表的尾插的一样。
④ 最后调用 AdjustUp 接口,传入目标数组,和插入的数据(即 size - 1)。
0x05 堆的删除(HeapPop)
堆的删除,因为在讲堆的插入时我们用大堆演示的,我们这里先用小堆来演示。
📌 删除的核心思路:删除堆,删除的是堆顶的数据。就是删除这个树的根。
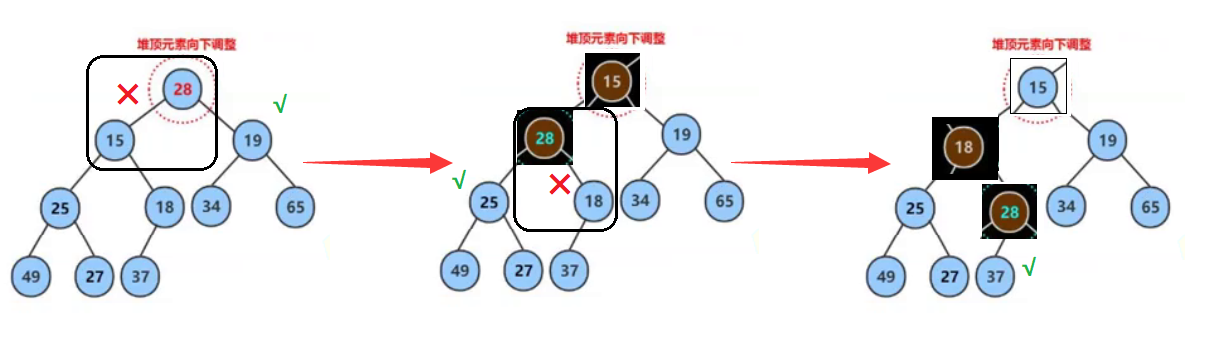
📚 将堆顶的数据跟最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
① 将堆顶元素与堆中最后一个元素进行交换。
② 删除堆中的最后一个元素。
③ 将堆顶元素向下调整到满足堆特性为止。
向下调整,把它调整成堆,跟左右孩子中小的那个交换。
结束条件(有一个成立即可):
① 父
小的孩子,则停止。
② 调整到叶子(因为叶子特征为没有孩子,左孩子下标超出数组范围,就不存在了)。
小堆向下调整(SmallAdjustDown)
void SmallAjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // 默认为左孩子
while(child < n) { // 叶子内
// 选出左右孩子中小的那一个
if(child + 1 < n && arr[child + 1] < arr[child]) {
child = child + 1;
}
// 如果孩子小于父亲(不符合小堆的性质)
if(arr[child] < arr[parent]) {
// 交换它们的值
Swap(&arr[child], &arr[parent]);
// 往下走
parent = child;
child = parent * 2 + 1;
} else { // 如果孩子大于父亲(符合小堆的性质)
// 跳出循环
break;
}
}
}
🔑 解读:
① 因为要考虑左孩子还是右孩子,我们可以定义两个变量,分别记录左孩子和有孩子。但是我们这里可以用更好的方法,只需要定义一个孩子即可。具体实现方法如下:首先创建 child,我们先默认它是左孩子,利用传进来的 parent 根据公式计算出 child 的大小:
因为我们暂且默认为左孩子,我们随后进入循环后要进行检查,看看是左孩子大还是右孩子大,这里我们只需要根据数组的性质,将 child + 1 即可得到右孩子的下标,从而方便我们进行比较。比较完毕后将 child 重新赋值,拿个孩子小就将 child 给谁。
② 一共有两个结束条件(出口),第一个结束条件是父亲小于孩子就停止,第二个结束条件是chi调整到叶子。所以,循环体判断部分根据我们分析的结束条件,如果调整到叶子就结束,我们接受了 n,也就是数组的大小,只要 child 超过数组的大小(child > n) 就结束,这是第一个出口。
③ 进入循环后,对比左孩子和右孩子哪一个更小,child 就交付给谁。这里还要注意的是,要防止孩子不存在的情况,如果 child + 1 比 n 大,就说明孩子不存在。所以我们再写 if 判断条件的时候就要注意了,我们加一个 child + 1 < n 的条件限制一下:
if(child + 1 < n && arr[child + 1] < arr[child]) {...}④ 确认好较小的孩子后,我们就可以开始比较孩子和父亲的大小了。如果孩子小于父亲,就不符合小堆的性质,我们就要交换它们的值。这里我们直接调用我们刚才写的 Swap 接口即可,这就是为什么在写向上调整的时候要我们单独把交换部分的代码写成函数的原因。
⑤ 交换完毕后,他们的值已经互相交换好了,这时我们要改变 parent 和 child 的指向,让它们往下走,parent = child ,child 再次根据公式算出新的 child 即可。
⑥ 设计下 if 的 else 部分,如果数组的 child 的值大于 parent 的值,说明符合小堆的性质了, break 跳出循环即可,这是第二个出口。
下上调整的接口写好了,我们现在可以实现堆的删除了:
💬 Heap.h
void HeapPop(HP* php);
💬 Heap.c
void HeapPop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
// 删除数据
Swap(&php->array[0], &php->array[php->size - 1]);
php->size--;
// 向下调整 [目标数组,数组的大小,调整位置的起始位置]
SmalljustDown(php->array, php->size, 0);
}🔑 解读:
① 首先检查 php 是否为空。
② 因为删除必须得有东西可删,这里肯定是要检查是否为空的,调用 HeapIfEmpty ,逻辑反操作符,断言数组不为空。
③ 因为删除堆,删除的是堆顶的数据,所以这里我们要在删除前让,删除数据根据我们的经验,直接 size - - 即可。
④ 最后调用 AdjustDown 接口,传入目标数组,数组的大小,和起始位置(即 0)。
❓ 如果我们想改成大堆呢?
💡 只需要改变一下判断条件即可:
① 选出左右孩子大的那一个。
② 小堆是所有父亲都小于孩子,大堆则是所有父亲都要大于孩子,我们来改一下:
大根堆向下调整(BigAdjustDown)
void BigAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // 默认为左孩子
while (child < n) { // 叶子内
// 选出左右孩子中大的那一个
if (child + 1 < n && arr[child + 1] > arr[child]) {
child++;
}
if (arr[child] > arr[parent]) { // 如果孩子大于父亲(不符合大堆的性质)
// 交换它们的值
Swap(&arr[child], &arr[parent]);
// 往下走
parent = child;
child = parent * 2 + 1;
}
else { // 如果孩子小于父亲(符合大堆的性质)
// 跳出循环
break;
}
}
}🔑 解读:很简单,只需要改一下判断的条件即可。
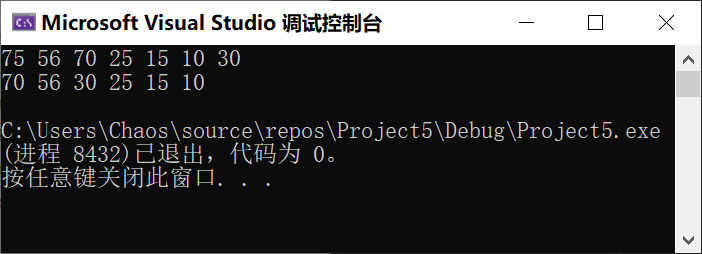
💬 Test.c
我们来测试一下刚才写的部分代码。
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
void HeapTest1() {
// 大根堆
int a[] = { 70, 56, 30, 25,15,10,75 };
HP hp;
HeapInit(&hp);
for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i) {
HeapPush(&hp, a[i]);
}
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
}
int main()
{
HeapTest1();
return 0;
}🚩 运行结果:
0x06 返回堆顶数据(HeapTop)
💬 Heap.h
HPDataType HeapTop(HP* php);💬 Heap.c
/* 返回堆顶数据 */
HPDataType HeapTop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
return php->array[0];
}🔑 解读:
① 首先检查传入的 php 是否为空,还要防止堆内没有数据。
② 返回堆顶,堆顶就是根,根的下标为 0,返回根即可。
0x07 统计堆的个数(HeapSize)
💬 Heap.h
HPDataType HeapTop(HP* php);💬 Heap.c
/* 统计堆的个数 */
int HeapSize(HP* php) {
assert(php);
return php->size;
}🔑 解读:
① 首先检查传入的 php 是否为空。
② 与其说统计堆的个数,不如说是返回堆的个数,因为根本就不需要统计,直接返回 size 就完事了。
四、完整代码
💬 Heap.h
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //指向动态开辟的数组
int size; //有效数据的个数
int capacity; //容量空间的大小
} HP;
/* 堆的初始化 */
void HeapInit(HP* php);
/* 堆的销毁 */
void HeapDestroy(HP* php);
/* 堆的打印 */
void HeapPrint(HP* php);
/* 判断堆是否为空 */
bool HeapIfEmpty(HP* hp);
/* 堆的插入 */
void HeapPush(HP* php, HPDataType x);
/* 检查容量 */
void HeapCheckCapacity(HP* php);
/* 交换函数 */
void Swap(HPDataType* px, HPDataType* py);
/* 大根堆上调 */
void BigAdjustUp(int* arr, int child);
/* 小根堆上调 */
void SmallAdjustUp(int* arr, int child);
/* 堆的删除 */
void HeapPop(HP* php);
/* 小根堆下调*/
void SmallAdjustDown(int* arr, int n, int parent);
/* 大根堆下调 */
void BigAdjustDown(int* arr, int n, int parent);
/* 返回堆顶数据*/
HPDataType HeapTop(HP* php);
/* 统计堆的个数 */
int HeapSize(HP* php);
💬 Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
/* 堆的初始化 */
void HeapInit(HP* php) {
assert(php);
php->array = NULL;
php->size = php->capacity = 0;
}
/* 堆的销毁 */
void HeapDestroy(HP* php) {
assert(php);
free(php->array);
php->capacity = php->size = 0;
}
/* 堆的打印 */
void HeapPrint(HP* php) {
for (int i = 0; i < php->size; i++) {
printf("%d ", php->array[i]);
}
printf("\n");
}
/* 判断堆是否为空 */
bool HeapIfEmpty(HP* php) {
assert(php);
return php->size == 0; // 如果为size为0则表示堆为空
}
/* 堆的插入 */
/* 检查容量 */
void HeapCheckCapacity(HP* php) {
if (php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : (php->capacity * 2); //第一次给4,其他情况扩2倍
HPDataType* tmpArray = (HPDataType*)realloc(php->array, sizeof(HPDataType) * newCapacity); // 数组扩容
if (tmpArray == NULL) { //检查realloc
printf("realloc failed!\n");
exit(EXIT_FAILURE);
}
//更新他们的大小
php->array = tmpArray;
php->capacity = newCapacity;
}
}
/* 交换函数 */
void Swap(HPDataType* px, HPDataType* py) {
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}
/* 大根堆上调 */
void BigAdjustUp(int* arr, int child) {
assert(arr);
// 首先根据公式计算算出父亲的下标
int parent = (child - 1) / 2;
// 最坏情况:调到根,child=parent 当child为根节点时结束(根节点永远是0)
while (child > 0) {
if (arr[child] > arr[parent]) { // 如果孩子大于父亲(不符合堆的性质)
// 交换他们的值
Swap(&arr[child], &arr[parent]);
// 往上走
child = parent;
parent = (child - 1) / 2;
} else { // 如果孩子小于父亲(符合堆的性质)
// 跳出循环
break;
}
}
}
/* 小根堆上调 */
void SmallAdjustUp(int* arr, int child) {
assert(arr);
// 首先根据公式计算算出父亲的下标
int parent = (child - 1) / 2;
// 最坏情况:调到根,child=parent 当child为根节点时结束(根节点永远是0)
while (child > 0) {
if (arr[child] < arr[parent]) { // 如果孩子大于父亲(不符合堆的性质)
// 交换他们的值
Swap(&arr[child], &arr[parent]);
// 往上走
child = parent;
parent = (child - 1) / 2;
} else { // 如果孩子小于父亲(符合堆的性质)
// 跳出循环
break;
}
}
}
void HeapPush(HP* php, HPDataType x) {
assert(php);
// 检查是否需要扩容
HeapCheckCapacity(php);
// 插入数据
php->array[php->size] = x;
php->size++;
// 向上调整 [目标数组,调整位置的起始位置(刚插入的数据)]
BigAdjustUp(php->array, php->size - 1);
}
/* 堆的删除 */
/* 小根堆下调*/
void SmallAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // 默认为左孩子
while (child < n) { // 叶子内
// 选出左右孩子中小的那一个
if (child + 1 < n && arr[child + 1] < arr[child]) {
child++;
}
if (arr[child] < arr[parent]) { // 如果孩子小于父亲(不符合小堆的性质)
// 交换它们的值
Swap(&arr[child], &arr[parent]);
// 往下走
parent = child;
child = parent * 2 + 1;
} else { // 如果孩子大于父亲(符合小堆的性质)
// 跳出循环
break;
}
}
}
/* 大根堆下调 */
void BigAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // 默认为左孩子
while (child < n) { // 叶子内
// 选出左右孩子中大的那一个
if (child + 1 < n && arr[child + 1] > arr[child]) {
child++;
}
if (arr[child] > arr[parent]) { // 如果孩子大于父亲(不符合大堆的性质)
// 交换它们的值
Swap(&arr[child], &arr[parent]);
// 往下走
parent = child;
child = parent * 2 + 1;
} else { // 如果孩子小于父亲(符合大堆的性质)
// 跳出循环
break;
}
}
}
void HeapPop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
// 删除数据
Swap(&php->array[0], &php->array[php->size - 1]);
php->size--;
// 向下调整 [目标数组,数组的大小,调整位置的起始位置]
/* SmallAdjustDown(php->array, php->size, 0); */
BigAdjustDown(php->array, php->size, 0);
}
/* 返回堆顶数据 */
HPDataType HeapTop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
return php->array[0];
}
/* 统计堆的个数 */
int HeapSize(HP* php) {
assert(php);
return php->size;
}
参考资料:
Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .
百度百科[EB/OL]. []. https://baike.baidu.com/.
📌 笔者:王亦优
📃 更新: 2021.11.26
❌ 勘误: 无
📜 声明: 由于作者水平有限,本文有错误和不准确之处在所难免,本人也很想知道这些错误,恳望读者批评指正!
本篇完。