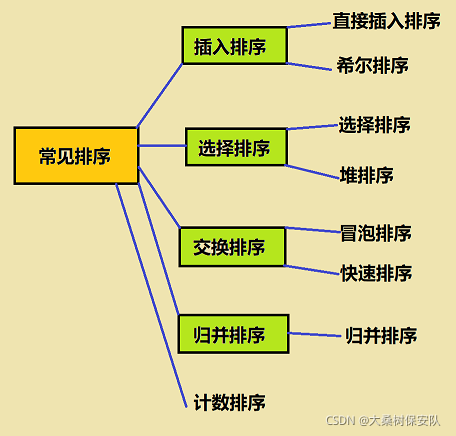
0.简介

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

排序实现的接口：

//打印序列
void PrintArray(int* a, int n);

//直接插入排序
void InsertSort(int* a, int n);

//希尔排序
void ShellSort(int* a, int n);

//选择排序
void SelectSort(int* a, int n);

//堆排序
void HeapSort(int* a, int n);

//冒泡排序
void BubbleSort(int* a, int n);

//快排
void QuickSort(int* a, int left,int right);
void QuickSortNonR(int* a, int left, int right);

//归并排序
void MergeSort(int* a, int n);
void MergeSortNonR(int* a, int n);

//计数排序
void CountSort(int* a, int n);

---

1.直接插入排序（Straight Insert Sort）

• 1.原理

是一种最简单的排序，将元素逐个插入到已排好序的有序表中，从而得到一个新的，容量增1的有序表。

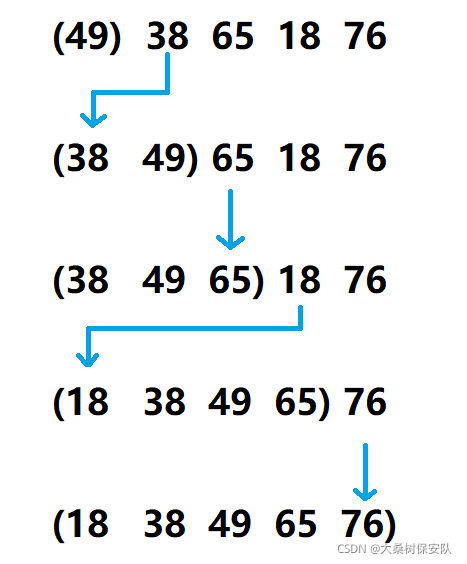
• 2.图示讲解

将r[i]与r[i-1],r[i-2],…,r[0],从后向前顺序比较，在往前比较的过程中同时后移比自身大的元素。

• 3.代码实现（升序）

void InsertSort(int* a, int n)
{
	int i;
	for (i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end>=0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];//比待插入元素更大的元素需要后移
				end--;//从后往前寻找插入点
			}
			else
			{
				break;//找到end后退出循环
			}
		}
		a[end + 1] = tmp;//在end之后插入
	}
}

• 4.复杂度分析

• 时间复杂度
  代码中的循环次数取决于待插元素与前i-1个元素的大小关系
  最好情况，序列原本已为顺序，只需遍历一遍数组，无需移动——O(N)
  最坏情况，序列为逆序，每次待插元素需要逐步走向队头，那么总的比较次数（移动次数）为一个等差数列的和，最后一个元素需要比较n-1次才能走到队头——O(n^2).

• 空间复杂度
  只需要一个记录待插元素的辅助空间tmp，所以空间复杂度为O(1).

稳定性：插入排序是稳定的排序算法，满足条件r[j] > r[j + 1]才发生交换，这个条件可以保证值相等的元素的相对位置不变

---

2.希尔排序（Shell’s Sort）

• 1.原理

希尔排序是插入排序的一种，又称缩小增量法。
希尔排序法的基本思想是：先选定一个整数gap，把待排序文件中所有记录分成n/gap个组，所有距离为gap的记录分在同一组内，并对每一组内的记录进行排序。
然后，gap折半，重复上述分组和排序的工作。当到达gap==1时（等同于直接插入排序），此时序列已基本有序，所有记录在统一组内排好成有序序列。
当面对大量数据时，希尔排序将比直接插入排序更具优势

• 2.图示讲解
  
  

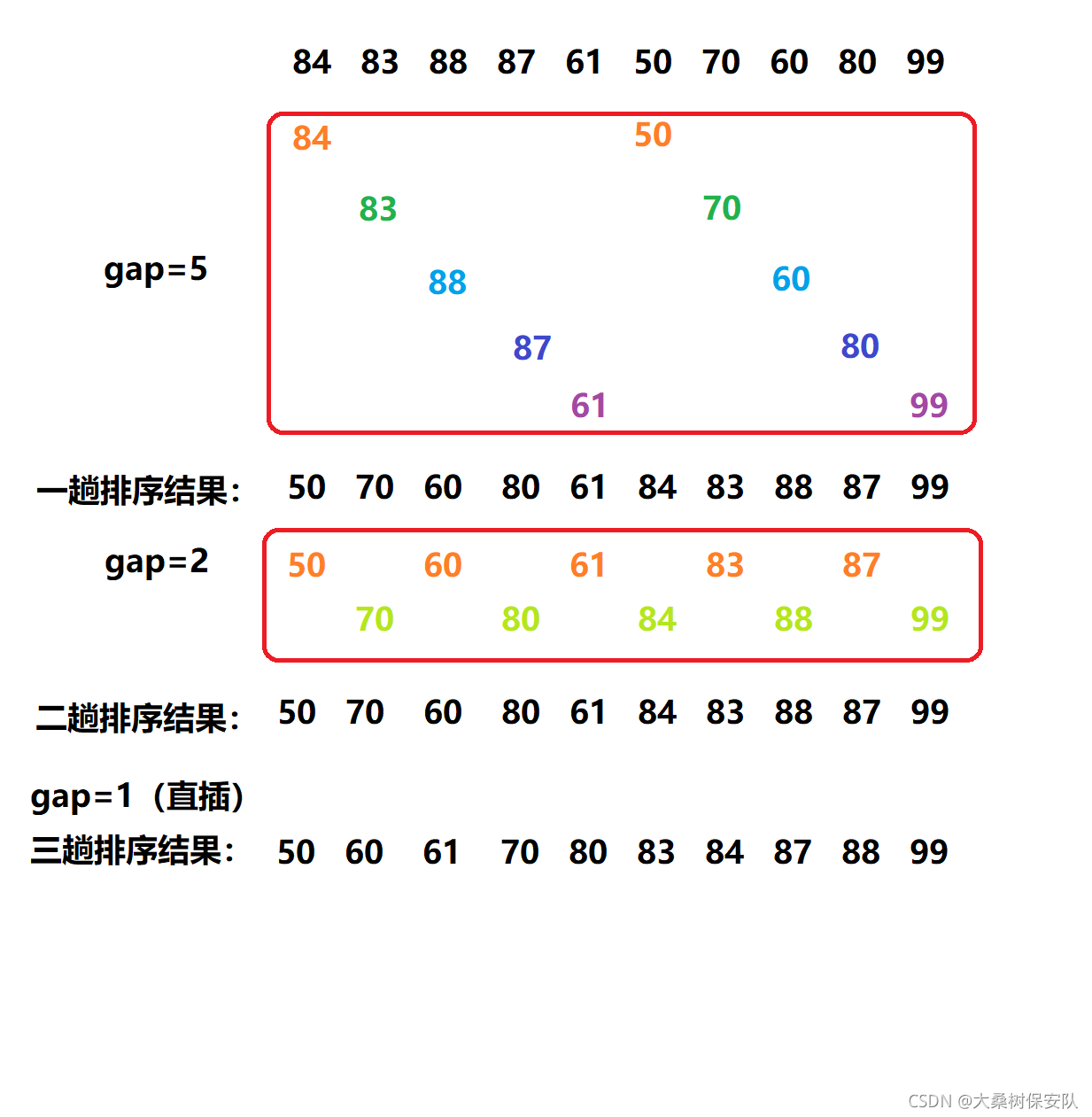
• 第一趟取增量gap=5，所有间隔为5的元素分在一组，在各个组中分别进行直接插入排序。

我们可以根据这个特性，先写出一部分代码：

for (int i = 0; i < n - gap; i++)
		{
			//单个数字
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}

• 第二趟增量取之前增量的一半，即gap=2，所有间隔为2的元素分在一组，在各个组中直接插入排序。
• 第三趟gap=1，对整个序列进行一趟直接插入排序，由于已基本有序，这次的直接插入排序将会省去不少时间。

• 3.代码实现

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 2;
		//单个gap组
		for (int i = 0; i < n - gap; i++)
		{
			//单个数字
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

• 4.复杂度分析

• 时间复杂度
  当gap>1时，元素不是一步步移动，而是跳跃式移动，当进行最后的直接插入排序时，序列以基本有序，只要做少量的比较和移动即可完成排序。希尔排序的时间复杂度取决于gap的选择，这涉及一些数学上尚未解决的难题。在前人大量的实验基础上推出，当序列长度n在特定范围内，时间复杂度为O(n^1.3),当n->∞时，可减少到O(n*log(n)).
• 空间复杂度
  只需要一个辅助空间——O(1)

• 稳定性分析

不稳定，相同的值预排时被分到不同的组里

---

3.选择排序

• 1.原理

在数组r[0…(n-1)]中，第一趟从r[0]开始，通过n-1次比较在n个元素中找到最小的元素并与r[0]互换。
第二趟从r[1]开始，通过n-2次比较，在n-1个元素中找到最小的元素并于r[1]互换。
依次类推，经过n-1趟，排序完成。

• 动图演示
  
• 代码实现
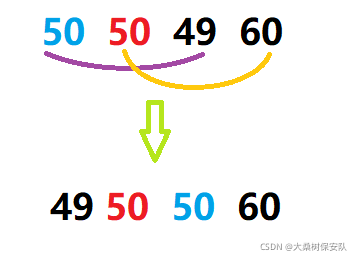
  这里我们使用双向选择排序，在每次遍历中同时选中最小与最大元素，分治当下序列的头和尾。

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}


void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int mini = begin, maxi = end;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		//互换函数
		Swap(&a[begin], &a[mini]);
		//begin==maxi时，最大的被换到了mini的位置了，需要对maxi调整
		if (begin == maxi)
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

• 4.复杂度分析

• 时间复杂度
  无论初始的序列排列如何，元素之间依然需要通过遍历去比较大小，确定单个最值的时间复杂度为等差数列之和(n^2/2),同时确定最大和最小值的时间复杂度(n ^2/4)。不管原序列是无序，有序或接近有序，选择排序的时间复杂度皆为O(n ^2),
  空间复杂度
  一个辅助空间或两个辅助空间——O(1)

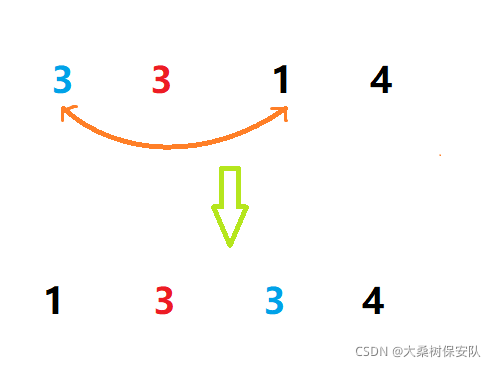
• 稳定性分析
  不稳定
  

---

4.堆排序

• 1.原理

堆的定义：简而言之，将数组按层序排成的完全二叉树，称之为堆
如果二叉树的双亲结点大于孩子结点——大根堆
如果二叉树的双亲结点小于孩子结点——小根堆

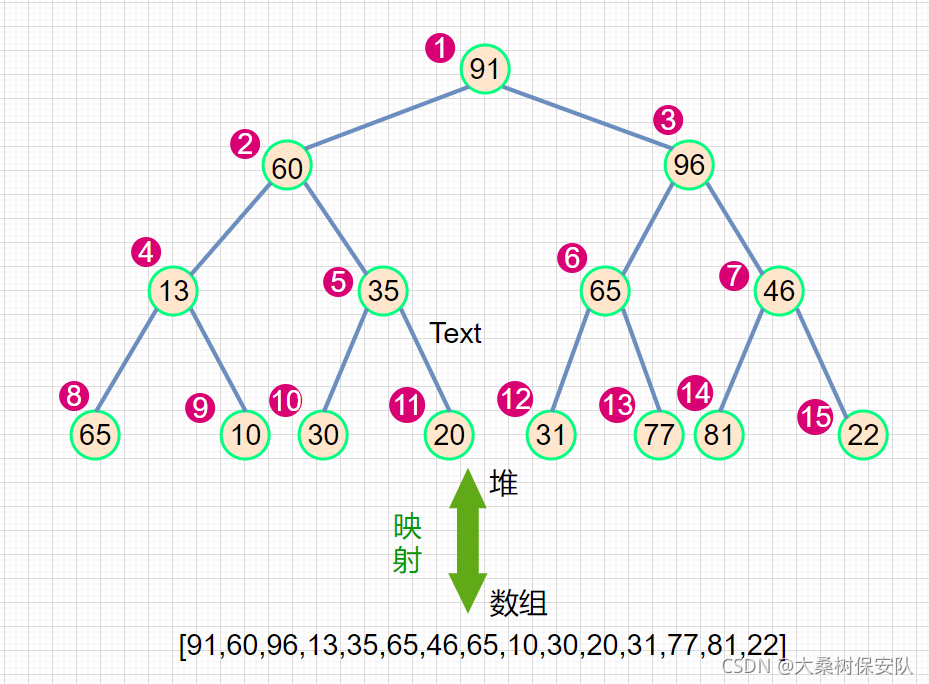
之后我们需要进一步调整，将堆调整成为大根堆(小根堆)。大小根堆可保证堆顶为当前数组的最值

那么我们如何对堆进行调整呢？

• 首先我们需要了解一下堆的性质
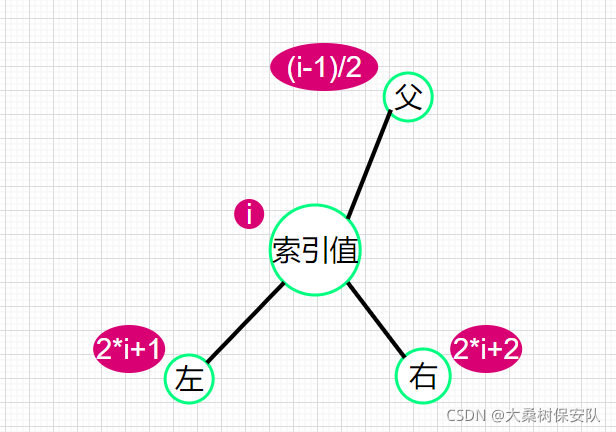
  如果当前索引值下标为i，
  双亲结点的下标 parent=(i-1)/2
  左孩子结点的小标 child1 =2*i+1
  右孩子结点的下标 child2 =2*i+2
  
  了解这一基本性质后，我们就可以对堆进行调整了。

以建大根堆作为演示

• 向下调整
  从最后一个非叶子结点parent开始，让其与孩子结点进行比较，如果孩子结点比k大，那么k便往下与孩子结点互换，直到孩子的下标越界，说明该结点调整结束。
  然后继续对上一个非叶子结点的子树进行向下调整，直到达到整个堆的根结点，堆调整结束。
• 最后一个非叶子结点的下标parent的计算
  数组长度为n，那么最后一个叶子结点下标为n-1，其双亲结点就是最后一个非叶子结点，于是parent=(n-1-1)/2

• 动图演示建立大根堆

- 单颗子树根结点向下调整的代码实现

//向下调整
void AdjustDown(int *a,int n,int parent)//a-数组，n-数组大小，parent-向下调整的起始位置
{
	int child = parent * 2 + 1;//完全二叉树必先有左孩子
	while (child < n)//当孩子越界时，说明双亲已达叶子结点，结束当前调整
	{
		if (child + 1 < n && a[child+1]>a[child])//找到两个孩子中的较大者
		{
			child++;
		}
		if (a[child] > a[parent])//如果孩子比双亲大则互换
		{
			Swap(&a[child], &a[parent]);
			parent = child;//双亲向下继续调整
			child = parent * 2 + 1;//孩子随着双亲一起改变
		}
		else
		{
			break;//双亲已比孩子大亦无必要调整，因为下面的子树先前已成大根堆
		}
	}
}

如果我们需要排为升序，则应建立大根堆。
同样我们需要排为降序，则应建立小根堆。
由堆的性质，我们只能唯一确定堆顶的是最值，
(1). 将得到的堆顶最值与堆尾元素互换，堆容量-1
(2).堆顶向下调整，选出剩余元素的最大值放置堆顶，
(3). 继续执行(1)(2)，直到堆容量为1，堆排序完成。

void HeapSort(int* a, int n)
{
	//建堆 升序建大堆
	int i = 0;
	//向下调整建堆
	for (i = (n-1-1)/2; i >=0; i--)//i从最后一个非叶子结点走向根结点
	{
		AdjustDown(a, n, i);
	}

	//把堆顶与堆尾互换不再理会，堆顶再向下调整
	for (i = 0; i < n; i++)
	{
		Swap(&a[0], &a[n - i - 1]);
		AdjustDown(a, n - i - 1, 0);
	}
}

• 2.动图演示 大根堆的堆排序
  

绿圈为已满足大根堆性质的树
紫圈为进行向下调整
黄圈为堆顶和堆尾交换过程
红圈为已排完序的元素

• 3.复杂度分析

堆排序的时间主要耗费在建初堆和调整堆时进行的反复筛选上。
建初堆的移动步数：
第h-1层，2^(h-2)个结点向下移动1层
…
第3层，2^(2)个结点，向下移动h-3层
第2层，2^(1)个结点，向下移动h-2层
第1层，2^(0)个结点，向下移动h-1层
T(n)=2^(0)* (h-1)+2 ^(1)* (h-2)+…+2^(h-2)1
利用错位相减法，得到T(n)=n-log2(n+1)≈n
建堆的时间复杂度为O(n)
调整堆需要将堆顶的元素不断的移向堆尾，则复杂度为元素个数二叉树高度——O(n*logn)
空间复杂度，只借助了一个辅助空间——O(1)

• 稳定性分析
  建堆会打乱原本的顺序，即使没有打乱，在调整堆时，排在靠前的相同元素会率先排到堆尾，打乱原有相对位置。
  所以堆排是不稳定的。

---

5.冒泡排序

它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

• 1.原理

• 比较相邻的两个数，如果第一个数比第二个数大，则两数交换。对之后的相邻元素进行同样的工作，从开始到最后一对，这样进行一次排序后，数据的最后一位会是最大值，第一次循环进行的次数为 r.length-1。之后对所有的元素重复以上的步骤，且以后每次循环的次数为r.length-1-i（i为循环第几次 ，i 从零开始）；重复上述步骤，直到排序完成

• 2.代码实现

void BubbleSort(int* a, int n)
{
	//优化
	//已经有序 提前结束
	for (int j = 0; j < n; j++)
	{
		int exchange = 0;
		for (int i = 1; i < n - j; i++)
		{
			if (a[i] < a[i - 1])
			{
				Swap(&a[i], &a[i - 1]);
				exchange = 1;
			}
		}
		if (exchange == 0)//没有发生过互换的情况，说明已经有序
		{
			break;
		}
	}
	
}

• 3.复杂度分析

时间复杂度
最好的时间复杂度O(n)–有序只需要遍历一遍
最差的时间复杂度O(n^2)——逆序，等差数列之和
空间复杂度，只借助了一个辅助空间——O(1)

• 稳定性分析
  比较两数在相等情况下不交换位置可保证稳定排序。

---

6.快速排序

• 1.原理

快速排序是由冒泡排序改进而得的。
在冒泡排序的过程中，每次遍历只对相邻元素进行比较，每次交换只能消除一个逆序。

如果能通过两个(不相邻的)元素的交换消除多个逆序，则会大大加快排序的速度，快速排序的一次交换可以消除多个逆序。

• 算法步骤
  单趟排序*（递归 or 迭代）：

//逻辑
void Partition()
{
	...
}

void QuickSort(int *a,int n)
{
	迭代 or 递归
	{
		Partition()//单趟排序函数
	}
}

• 单趟排序的思想（重要）

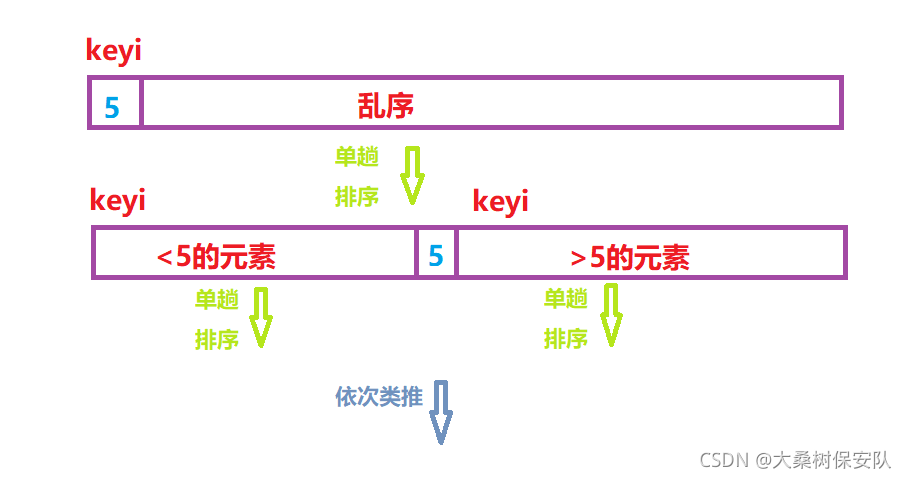
a.在序列的n个元素中，选择一个元素（一般选择第一个元素）作为枢轴，将其设为关键字keyi，在经历一次单趟排序后，所有小于keyi的元素交换到前面，把所有大于keyi的元素都交换到后面，单趟排序完成。

b.然后，将待排序的元素以keyi为界，分为左右两个子表，再分别对左右子表重复上述步骤。

c.直至每个子表不含元素或只有一个元素时（控制结束条件），排序完成。

• 单趟排序的方法

我们有三种方法可以完成单趟排序这一步骤，分别为Hoare算法，pivot法(挖坑法)和前后指针法。

> Hoare算法

a.选定下标作为基准值keyi，一般将keyi定在左端或者右端
b.我们再选定两个指针left，right分别位于序列的左侧和右侧。
c.如果keyi定在左侧则right先向左边遍历，如果keyi定在了右侧则left先向右边遍历。
d.这里我们假设keyi定在左侧，right先开始向左遍历，直至遇到比a[keyi]小的值则停下。然后left开始向右遍历，遇到比a[keyi]大的值则停下。然后互换左右下标对应值，Swap(&a[left],&a[right])。
e.然后继续right先走，left后走，直至left==right时，Swap(&a[keyi],&a[left]),这样便完成了单趟排序。

• 动图演示
  

这里的p也就是前文中提到的keyi，不过这里设置在了右端（a[keyi]为6），可以发现left先开始了遍历，找到了比keyi大的值，a[left]
为8，right随后找到了比keyi小的值，a[right]为4，两者调换完后继续遍历，直到left撞上right，将left和right共同指向的值9，与a[keyi]互换，完成单趟遍历。

• hoare代码实现

int Partition1(int* a, int left, int right)
{
	int keyi = left;//将keyi定在左侧，则右端先走，反之则左端先走
	while (left < right)
	{
		//右端先走,对于升序，找到比a[key]小的值则停下
		while (right > left && a[right] >= a[keyi])//保证是大于等于号
		{
			right--;
		}
		//left找比a[key]大的值停下
		while (left < right && a[left] <=a[keyi])//保证是小于等于号
		{
			left++;
		}
		Swap(&a[left], &a[right]);//交换左右，比keyi小的放左边，大的放右边
	}
	Swap(&a[keyi], &a[left]);
	return left;
}

---

> 挖坑法

• 具体思路：
  a.以左端作为基准值，将下标记为关键字pivot（枢轴），令keyi=a[pivot]。
  b.分别用关键字left和right记录左右端下标。
  c.right往左遍历，遇到比keyi小的数字时，将a[right]填入a[pivot]中，
  再让pivot=right(将坑位留在right处)。
  d.此时让left往右遍历，遇到比keyi大的数字，将a[left]填入a[left]中，
  再让pivot=left（将坑位留在left处）。
  e.之后依旧是right先动，left后动，直至left与right重合（此时left==right，right= =pivot）,使a[pivot]=keyi,单趟排序结束。

• 动图演示
  

• 代码实现

//单趟排序的第二种方法——挖坑法
int Partition2(int* a ,int left, int right)
{
	int keyi=a[left];
	int pivot = left;
	while (left < right)
	{
		//key在左端，则从右端开始找
		//右边找小，放到左边的坑中，自己再成坑
		while (left < right && a[right] >= keyi)
		{
			right--;
		}
		a[pivot] = a[right];
		pivot = right;
		//左边找大，放到右边的坑中，自己再成坑
		while (left < right && a[left] <= keyi)
		{
			left++;
		}
		a[pivot] = a[left];
		pivot = left;
	}
	a[pivot] = keyi;
	return pivot;
}

---

> 前后指针法

• 基本原理
  a.初始化：选择一端下标设为基准值keyi，需要两个指针，一个在前一个在后，分别用cur表示前指针，prev表示后指针(这里的指针的意思是待排序数列的下标)，我们规定cur在prev的后一个位置。prev指向这个数列开始的第一个，cur指向prev的后一个位置。
  b.如果cur的值大于基准值a[key]，这时只让cur++,如果a[cur]小于基准值，这时我们让prev++后，判断是否与cur的位置相等，若相等，cur继续向后遍历，若不相等，则交换cur和prev的值。

c.直到cur超过序列末尾时，我们再交换prev和基准值，这样基准值的位置也就确定了。

• 动图演示
  
• 代码实现
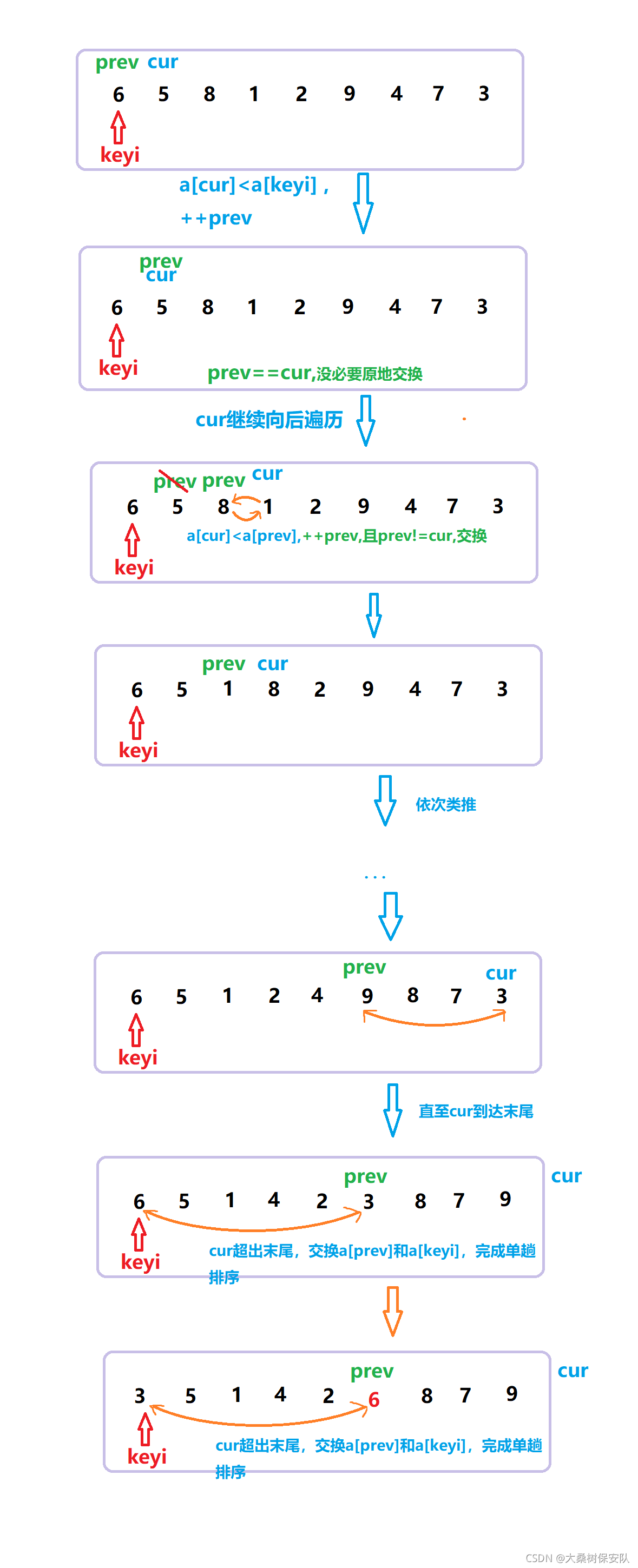
  相较于前两个方法，前后指针法的代码实现起来更为简介

keyi选在左端，那么cur从left+1开始 走到right，prev从cur-1开始。
cur走到终点时，[left+1,prev]都是比a[keyi]小的数字，[prev+1,right]都比a[keyi]大。
所以a[prev]和a[keyi]互换，使a[keyi]正确落位。

//以左端为keyi
int Partition3(int* a, int left, int right)
{
	int keyi = left;
	int cur = left + 1, prev = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && (++prev)!=cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	return prev;
}

如果以右端为keyi则有小小的改动

keyi选在右端，那么cur从left开始 走到right-1，prev从cur-1开始。
cur走到终点，[left,prev]都是比a[keyi]小的数字，[prev+1,right-1]都比a[keyi]大。
所以a[keyi]和a[prev+1]互换，以使a[keyi]正确落位。

int Partition4(int* a, int left, int right)
{
	int keyi = right;
	int cur = left, prev = left-1;
	while (cur <= right-1)
	{
		if (a[cur] < a[keyi] && (++prev) != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[++prev], &a[keyi]);
	return prev;
}

---

• 单趟排序的优化——三数取中法
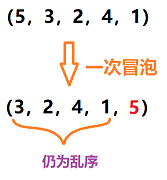
  如果每次选择的keyi能够在单趟排序后排入序列的中间位置，可以大大降低时间复杂度。因为左右子表均分可以降低“树”的高度，然而原先有序的序列会大大降低快速排序的速度，keyi每次原地不动，时间复杂度与选择排序一致，如图所示：
  
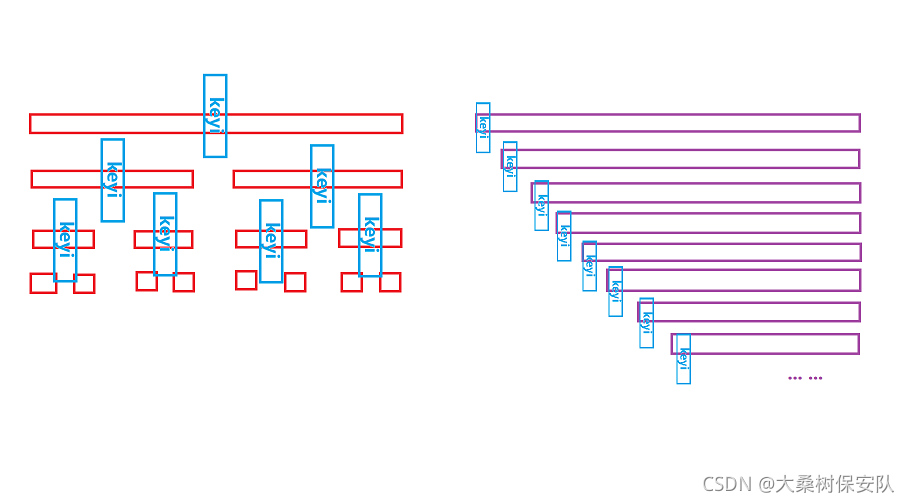
  有序与无序的快排对比
  

为防止遇到序列原本有序的情况，可以预先改变首端的keyi对应的值

//所以需要调整key的位置，使其值在位于序列的中间——三数取中法（找出中间大小的值）

int GetMidindex(int*a,int left,int right)
{
	int mid = (left + right) >>1;
	//int mid=left+((right-left)>>1);//可以防止left+right的和超过int的范围,>>移位效率比较高
	if (a[left] < a[mid])
	{
		if (a[right] > a[mid])
		{
			return mid;
		}
		else if(a[right]>a[left])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else //a[left] > a[mid]
	{
		if (a[right] < a[mid])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
}

在单趟排序前可以先使用三数取中，再进行排序

---

- 外层循环

1.快排递归

使用递归进行左右子表的单趟排序 （小区间优化的目的也是减少“树”的高度）

//O(n*logn)
void QuickSort(int* a, int left,int right)
{
	if (left >= right)
	{
		return;
	}

	//小区间优化，取消最后几层的递归
	if (right - left +1< 100)
	{
		//选择插入排序，将小区间直接捋顺
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int mid = Partition1(a, left, right);
		//int mid = Partition2(a, left, right);
		//int mid = Partition3(a, left, right);
		//int mid = Partition4(a, left, right);
		QuickSort(a, left, mid - 1);
		QuickSort(a, mid + 1, right);
	}
}

2.快排迭代（栈模拟实现）

将左右区间，压入栈中，每释放一个区间，就让该区间的左右子区间压入栈中，区间内不含元素则不压入栈，直到栈空为止。

//快排的非递归 (栈模拟实现)
	//将左右形成的区间压栈  --[0,9]
	//出栈一个区间，得到mid（每次得到mid的过程，就是将有序时mid位置的值落位的过程） --假设 mid=5
	//分别将 mid的 右边的区间 和 左边的区间压栈 --[0,4],[6,9]
	//如果mid左右不成区间，则无法压栈
	//如此，直到栈空
#include "Stack.h"
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	//将区间进栈
	StackPush(&st, left);
	StackPush(&st, right);
	while (!StackEmpty(&st))
	{
		int post_right = StackTop(&st);
		StackPop(&st);
		int post_left = StackTop(&st);
		StackPop(&st);
		int mid = Partition1(a, post_left, post_right);
		//得到两个区间
		//[post_left,mid-1] mid [mid+1,post_right]
		if (mid + 1 < post_right)
		{
			StackPush(&st, mid + 1);
			StackPush(&st, post_right);
		}
		if (mid - 1 > post_left)
		{
			StackPush(&st, post_left);
			StackPush(&st, mid-1);
		}
	}

	StackDestroy(&st);
}

有关栈的函数可以参考博客——C语言数据结构(4)——栈
源代码戳这里
用栈的思想解决快排，就像是深度优先解决左右区间
而使用队列的话，更像是“层序”解决左右子区间，有兴趣的读者可以自己尝试下。

• 复杂度分析

• 时间复杂度
  快排的趟数取决于递归树的或者栈的深度
  最好情况类似于折半查找——O(nlog2n)
  最坏情况类似于选择排序——O(n^2)
  由三数取中优化后，理论证明快排平均时间复杂度为O(nlog2n)
• 空间复杂度
  执行快排时需要一个栈来存放相应数据，栈的深度与递归树的深度一致，所以最好情况是O(log2n),最坏情况为O(n)

---

7.归并排序

• 原理

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。
自然我们就联想到使用递归的方法来实现归并排序，解决一棵树就先解决他的子树，解决一个序列的排序，就从解决其左右子序列的排序开始，
当然之后我也会讲解非递归的归并排序

• 分而治之

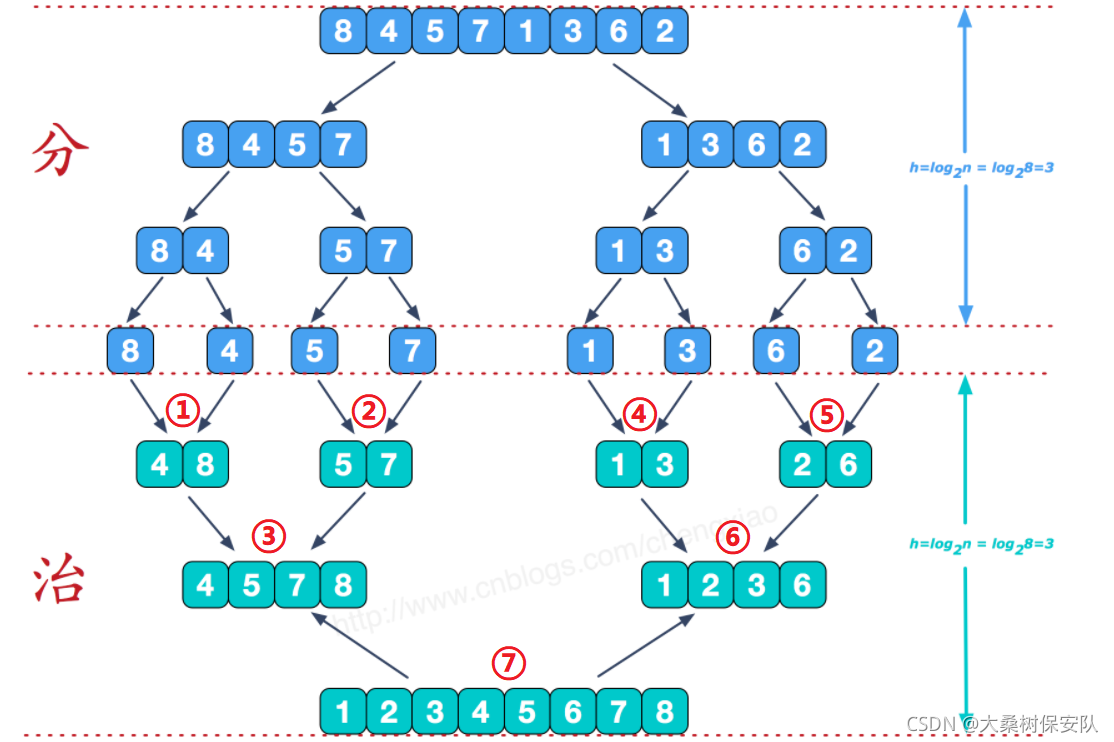
• 分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

• 治阶段我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

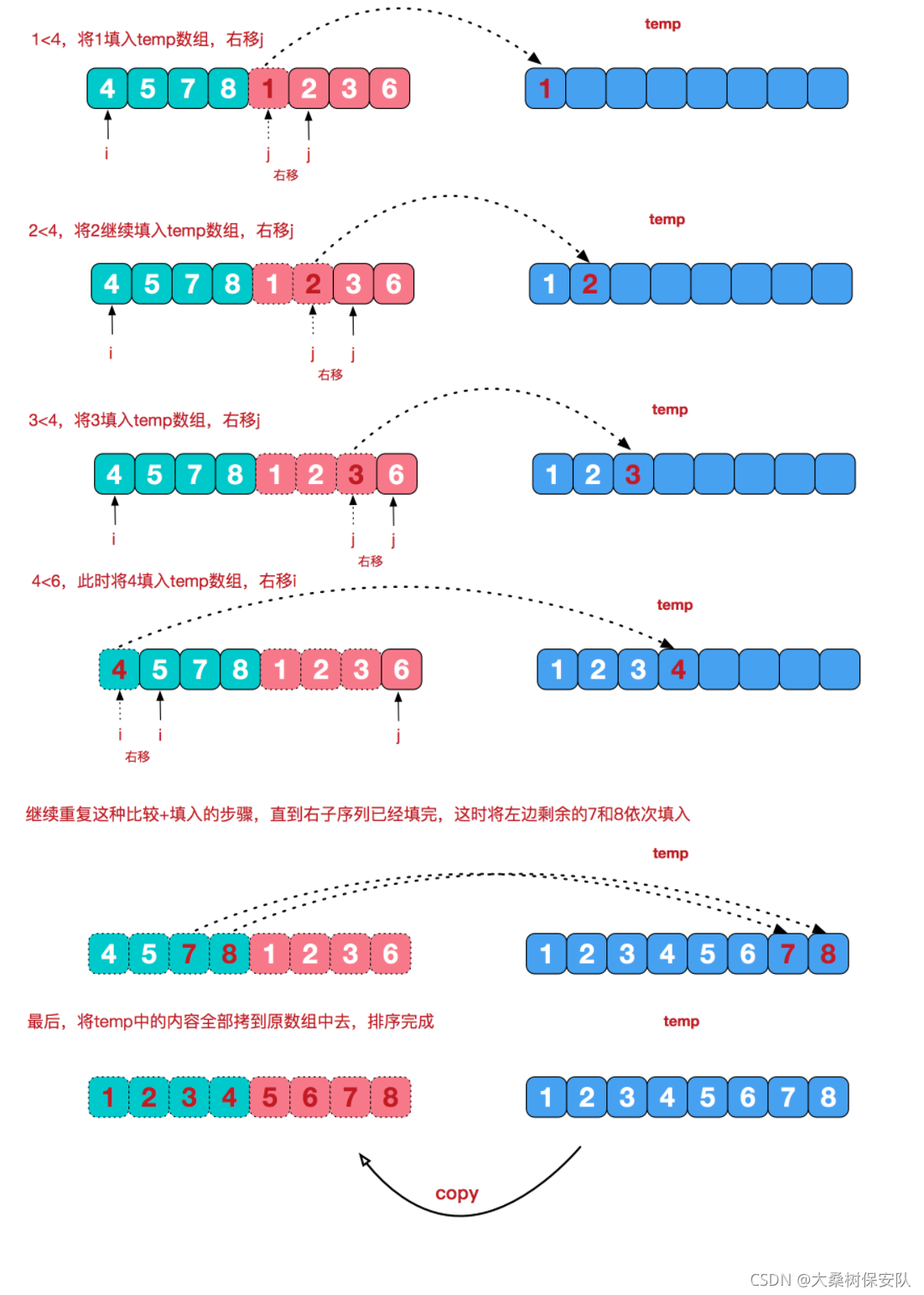
• 动图演示
  
  递归的思想是深度优先

1.归并递归

• 代码实现

//递归（深度）
//子函数
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left == right)
	{
		return;
	}
	int mid = left + ((right - left) >> 1);//取left和right的中点
	//[left,mid] [mid+1,right] 
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid+1,right, tmp);
	int begin1 = left, end1 = mid;
	int begin2 = mid+1, end2 = right;
	int index = left;//注意复制到tmp数组中的位置，是随着区间位置改变的
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}
	//注意每次归并都要拷贝回原数组 否则原数组仍处于无序状态，就不能归并在一起
	for (int i = left; i <=right; i++)
	{
		a[i] = tmp[i];
	}
}

//主函数
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	assert(tmp);

	_MergeSort(a, 0,n-1, tmp);

	free(tmp);
	tmp = NULL;
}

此时会有同学问了，如果归并的序列的元素数量不是2的指数级的数量，即不是2，4，8，16…那还能继续完成归并吗？
那么我们还是通过递归算法的动图来观测下（此时序列有九个元素）

你发现其中的秘密了吗？

---

• 归并排序的非递归实现

非递归的思想

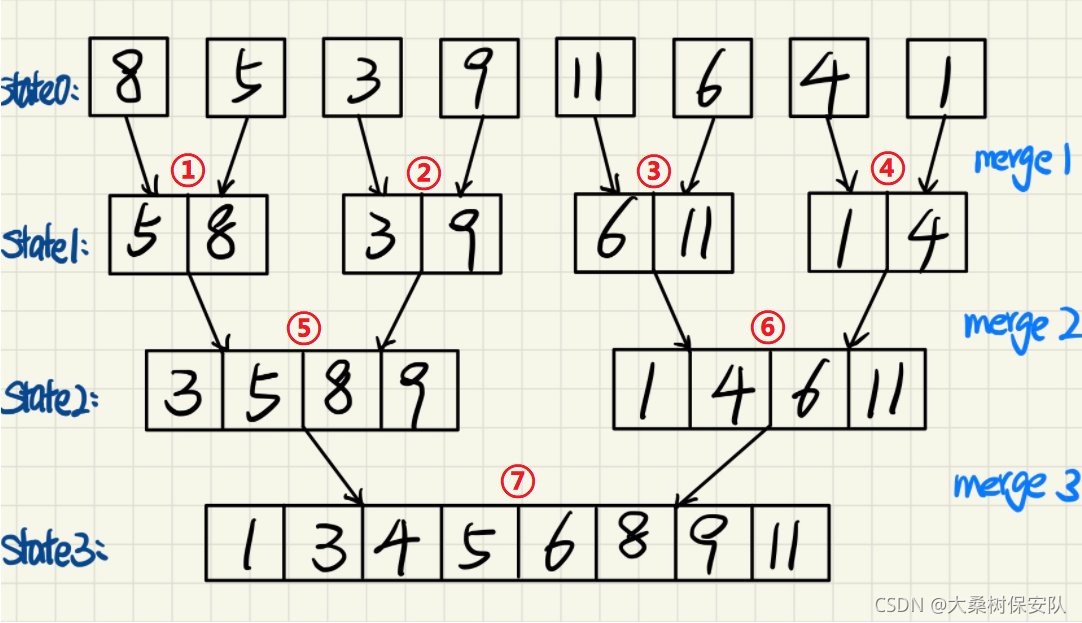
• 初始状态时，两两合并，即每次合并得到的都是有序的数组。
  两两合并的规则是：将两个相同序列长度的序列进行合并，合并后的序列长度*2。

• 第一趟合并（merge 1）进行了4次归并，得到了4个有序的数组：“5, 8”，“3, 9”，“6, 4”，“1, 4”（每个合并后的序列长度为2）

• 第二趟合并（merge 2）调用了2次归并，得到了2个有序的数组：“3, 5, 8, 9”，"1, 4, 6, 11’’（每个合并后的序列长度为4）

• 以此类推，经过多次合并最终得到有序的数组，也就是State3。

• 代码的逻辑框架

void MergeSortNonR(int* a,int n)
{
	...
	while(gap<n)//控制层数，即每次归并一层序列的总趟数
	{
		//一趟归并的次数
		for()//控制两个归并序列的区间
		{
			//两两合并
		}
	}
}

非递归的实现如同层序遍历一棵二叉树

2.归并迭代

• 代码实现

//归并的非递归(层序——广度)
//间距为1归并 ，然后间距为2归并... 
void MergeSortNonR(int* a, int n)
{
	PrintArray(a, n);
	int* tmp = (int*)malloc(sizeof(int) * n);
	assert(tmp);
	int gap = 1;
	while (gap<n)
	{
		printf("gap=%d\n", gap);
		int i = 0;
		for (i = 0; i <= n-2*gap; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;//[i,i+gap-1]
			int begin2 = i + gap, end2 = i + 2 * gap - 1;//[i+gap,i+2*gap-1]
			int index = begin1;
			printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			for (int j = i; j <= i + 2 * gap - 1; ++j)
			{
				a[j] = tmp[j];
			}

		}
		printf("i=%d\n", i);	
		PrintArray(a, n);
		gap *= 2;
	}
	free(tmp);
}

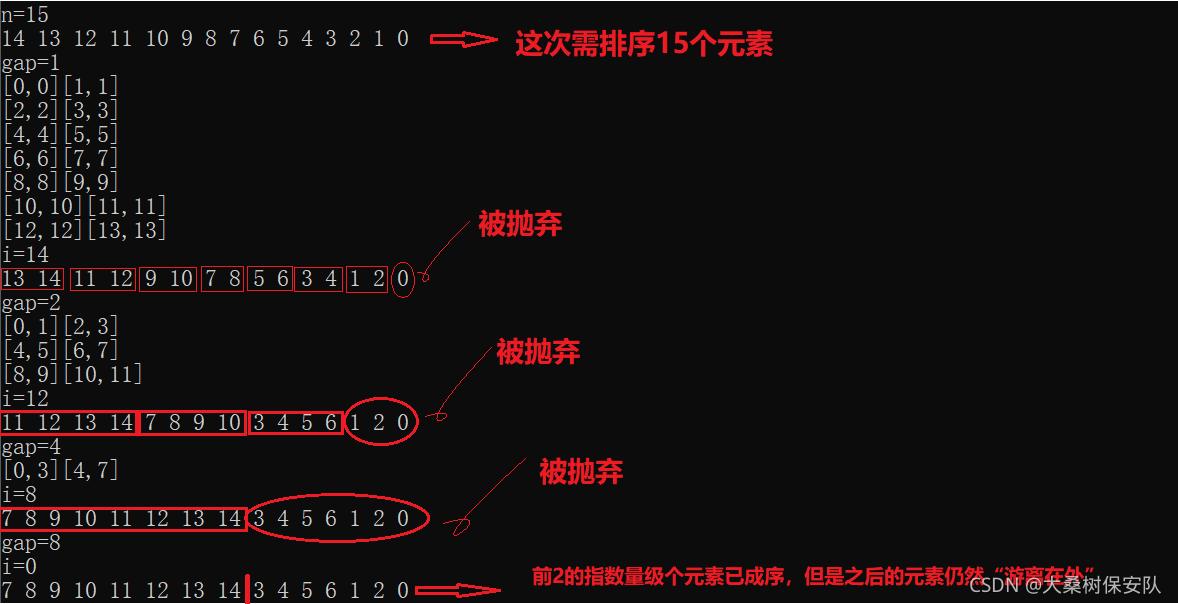
我们看下结果

• 你以为这样就结束了吗？
  之前我们说过递归法的归并排序可以解决元素数量不是2的指数量级的情况，那非递归是否可可以呢？我们试试看。
  
  而且我们还发现了一个规律：
  //非递归的瑕疵
  //非递归能很好的处理数据量为2^i的个数的序列，一旦不符合数量，就会造成
  //a.超过偶数个，则无法管理超出的偶数个数据（但超出的元素可以自成序）
  //b.超过奇数个，除了和超出偶数个有一样的弊病,且无法管理最后一个被孤立的数据。

• 下面我们对非递归代码进行修正

在for循环体后面添加一个判断

if(i<n-1)

如果满足条件，即说明在2^i的个数后还存在数字待归并排序！
哪两个区间进行归并呢？
Answer：[i,i+gap],[i+gap-1,n-1]

void MergeSortNonR(int* a, int n)
{
	PrintArray(a, n);
	int* tmp = (int*)malloc(sizeof(int) * n);
	assert(tmp);
	int gap = 1;
	while (gap<n)
	{
		printf("gap=%d\n", gap);
		int i = 0;
		for (i = 0; i <= n-2*gap; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;//[i,i+gap-1]
			int begin2 = i + gap, end2 = i + 2 * gap - 1;//[i+gap,i+2*gap-1]
			int index = begin1;
			printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			for (int j = i; j <= i + 2 * gap - 1; ++j)
			{
				a[j] = tmp[j];
			}

		}
		printf("i=%d\n", i);
		
		//剩下的n-gap个数是没排过序的
		PrintArray(a, n);
		printf("对剩余%d个数据进行归并\n",n-i);
		if (i < n-1)
		{

			//归并程序
			//两个范围——[i,i+gap-1][i+gap,n-1]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = n-1;
			int index = begin1;

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			for (int j = i; j <n; ++j)
			{
				a[j] = tmp[j];
			}
		}

		PrintArray(a, n);
		gap *= 2;
	}

	free(tmp);
}

• 结果
  
• 复杂度分析

• 时间复杂度 O(nlog2n)
• 空间复杂度,需要等量的辅助存储空间——O(n)

• 稳定性
  归并排序是稳定的。

---

8.计数排序

• 原理

这种排序算法不是基于元素比较，而是利用数组下标来确定元素的正确位置。
我们假定待排序序列的大小范围在0~10之间：
那么这些整数的值肯定是在0到10这11个数里面。于是我们可以建立一个长度为11的数组，数组下标从0到10，元素初始值全为0，如下所示：

先假设20个随机整数的值是：9, 3, 5, 4, 9, 1, 2, 7, 8,1,3, 6, 5, 3, 4, 0, 10, 9, 7, 9
比如第一个整数是9，那么数组下标为9的元素加1：

第二个整数是3，那么数组下标为3的元素加1：

依次类推：

数组中的每一个值，代表了数列中对应整数的出现次数。

有了这个统计结果，排序就很简单了，直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次：
0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10
这就是计数排序的基本过程，它适用于一定范围的整数排序。在取值范围不是很大的情况下，它的性能在某些情况甚至快过那些O(nlogn)的排序，例如快速排序、归并排序。

• 动图展示
  
• 代码实现

//计数排序（哈希）——适合数据大小范围比较集中的数组   O(Max(N,Range))
//范围较大，或是浮点数都不适合

void CountSort(int *a,int n)
{
	int max = a[0], min = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	assert(count);

	//统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

• 复杂度分析

• 时间复杂度——O(MAX(n,range))
• 空间复杂度——O(range)

• 稳定性分析——不稳定

---

复杂度与稳定性总结

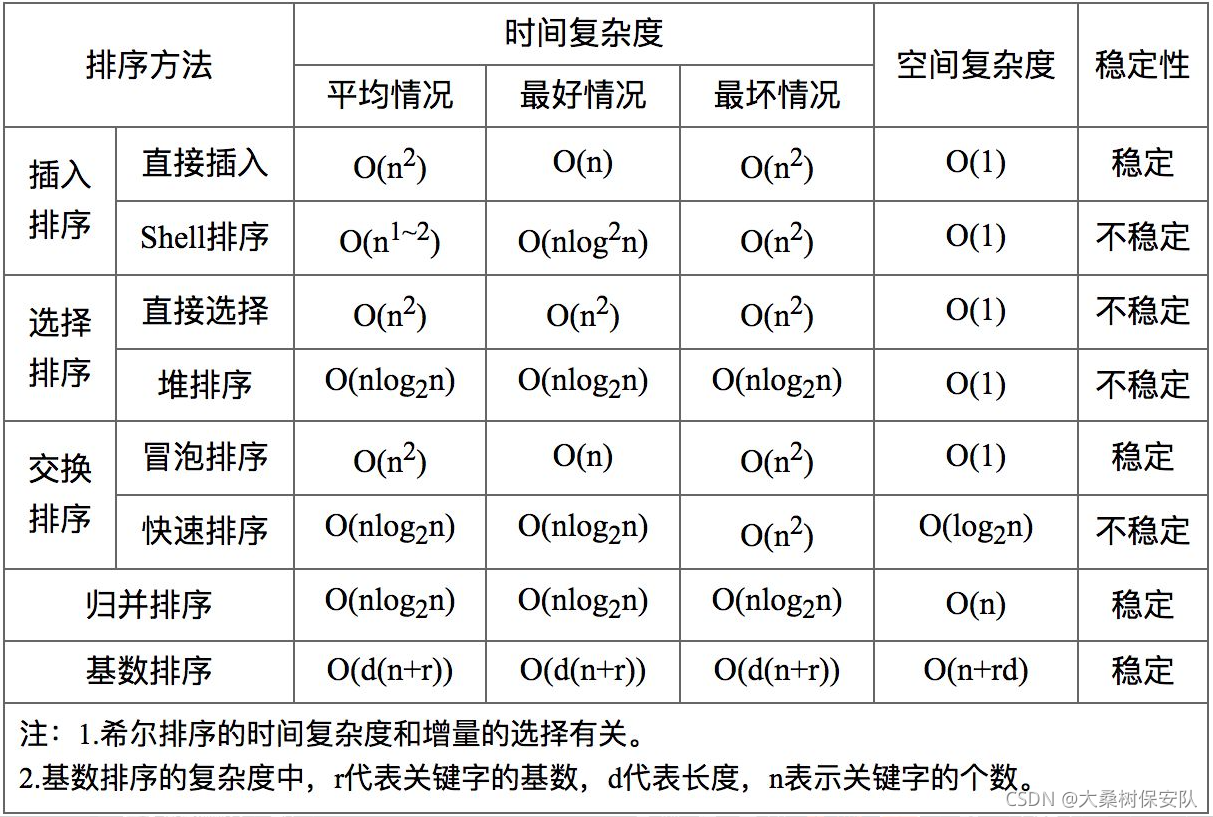
青山不改 绿水长流