当前位置：首页 » 《随便一记》 » 正文

数据结构之链表_一个山里的少年的博客

15 人参与  2022年05月14日 17:40  分类 : 《随便一记》  评论

点击全文阅读


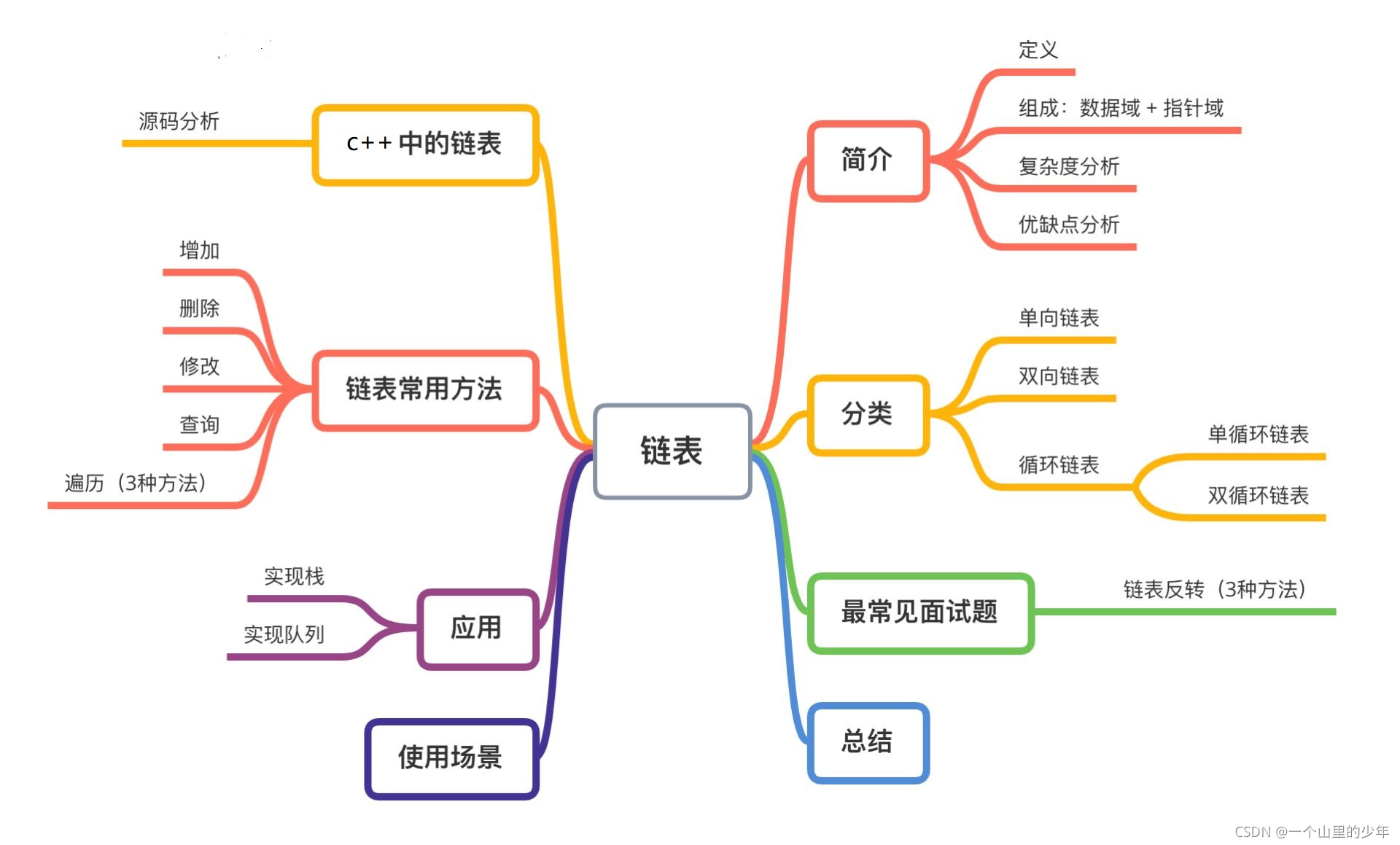
目录

1.链表的分类：

2.单链表的基本概念和性质：

链表的创建和遍历

 单链表的尾部插入

单链表的头部插入：

单链表pos位置后面插入：

单链表尾删

单链表头删

单链表pos位置删除：

单链表的查找：

单链表的销毁：

1.链表的分类：

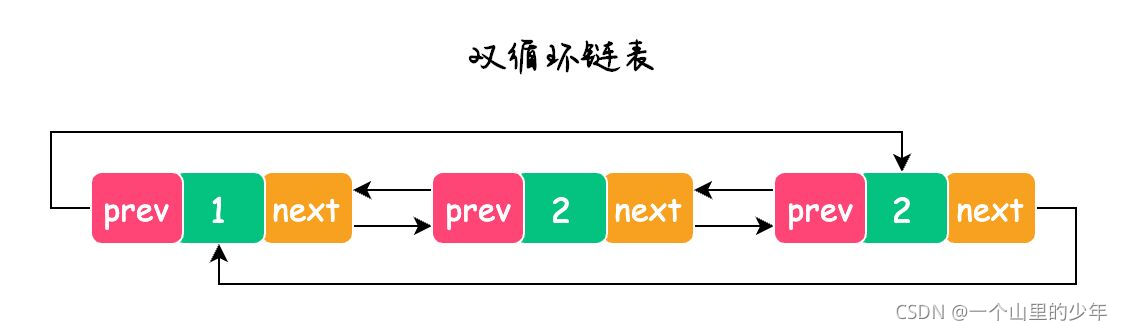
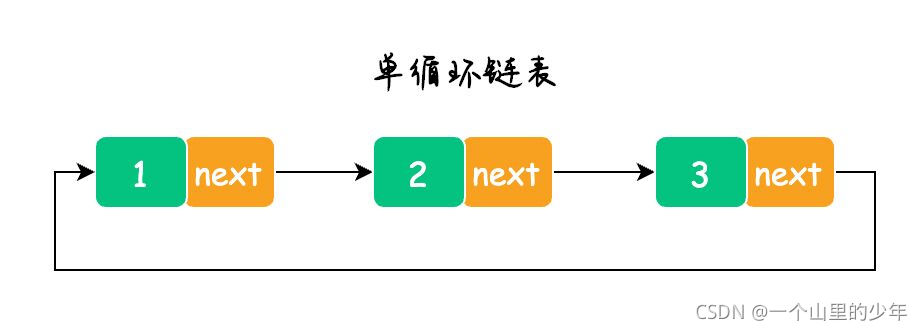
1.单向或者双向

2. 带头或者不带头

3. 循环或者非循环

4. 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。2. 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带来很多优势，实现反而简单

单链表

2.单链表的基本概念和性质：

1.1：单链表概念：

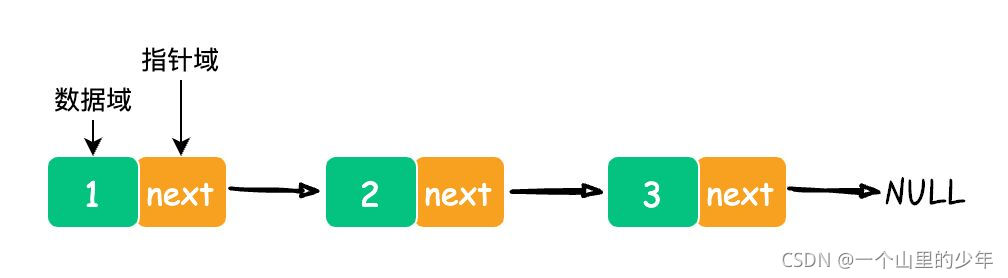
链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) + 指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

以“结点的序列”表示线性表称作线性链表（单链表），单链表是链式存取的结构。

1.2单链表的存储方法：

链接方式存储的线性表简称为链表（Linked List）。

链表的具体存储表示为：

① 用一组任意的存储单元来存放线性表的结点（这组存储单元既可以是连续的，也可以是不连续的）

② 链表中结点的逻辑次序和物理次序不一定相同。为了能正确表示结点间的逻辑关系，在存储每个结点值的同时，还必须存储指示其后继结点的地址（或位置）信息（称为指针（pointer）或链(link)）

链式存储是最常用的存储方式之一，它不仅可用来表示线性表，而且可用来表示各种非线性的数据结构。

链表的创建和遍历

1.单链表中结点的定义

typedef int SLTDataType;
struct SLTNode
{
	SLTNode(SLTDataType x)
		:next(nullptr),val(x)
	{}
	SLTNode* next;
	SLTDataType val;
};

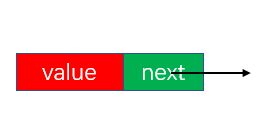
2.单链表内部结构：

单个节点：

 2.单链表的创建：

对应代码：

SLTNode* CreateSLTNode(SLTDataType x)
{
	SLTNode* newnode = new SLTNode(x);
	newnode->next = nullptr;
	newnode->val = x;
	return newnode;
}

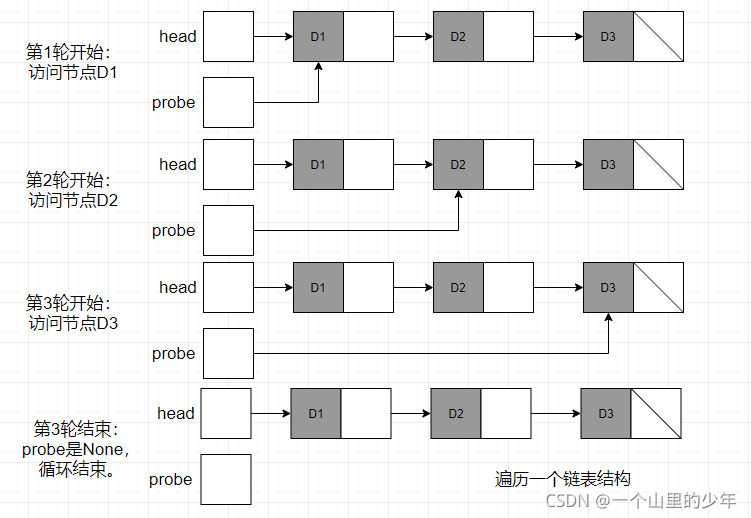
3.单链表的遍历：

void SLTNodePrint(SLTNode* head)
{
	SLTNode* probe = head;
	while (cur)//不为空则继续遍历
	{
		cout << probe->val << "->";//打应其数据
		probe =probe->next;
	}
	cout << "nullptr" << endl;

}

 单链表的尾部插入

实现思路：

1.如果链表没有头结点，新结点直接成为头结点。

2.如果有头节点则需要先找到链表当前的尾结点，并将新结点插入到链表尾部。

SLTNode* CreateSLTNode(SLTDataType x)//创建节点
{
	SLTNode* newnode = new SLTNode(x);
	newnode->next = nullptr;
	newnode->val = x;
	return newnode;
}



void SLTNodePushBack(SLTNode*&phead,SLTDataType x)
{
	SLTNode* newnode = CreateSLTNode(x);
	if (phead == nullptr) {//如果一个节点也没有则此时我们需要创建节点
		
		phead = newnode;
		return;
	}

	SLTNode* tail = phead;
	while (tail->next)//找尾
	{
		tail = tail->next;
	}

	tail->next = newnode;//链接
}

单链表的头部插入：

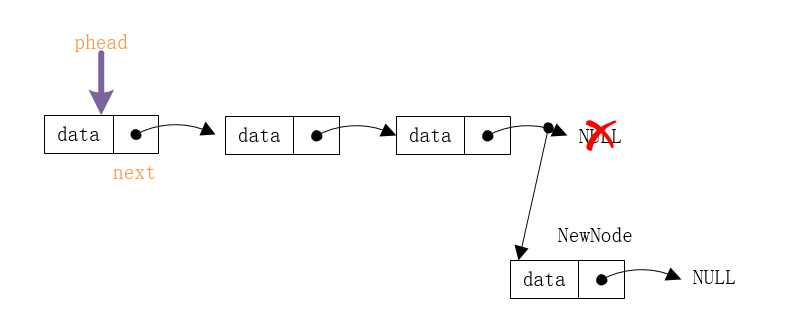
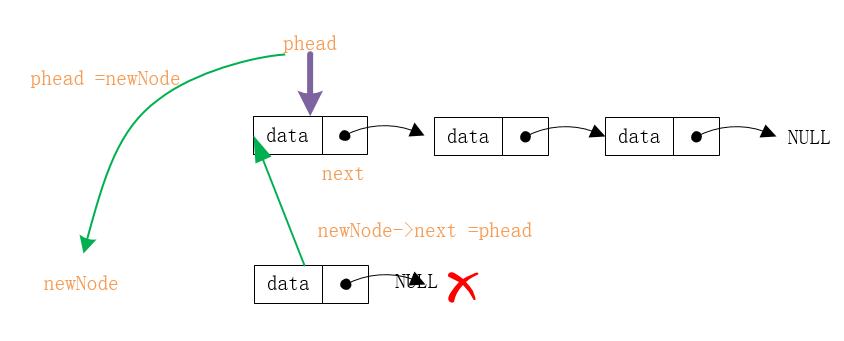
1.如果链表没有头结点，新结点直接成为头结点。

2.否则新结点的next直接指向当前头结点，并让新结点成为新的头结点。


SLTNode* CreateSLTNode(SLTDataType x)
{
	SLTNode* newnode = new SLTNode(x);
	newnode->next = nullptr;
	newnode->val = x;
	return newnode;
}



void SLTNodePushFront(SLTNode*& phead,SLTDataType x)
{
	SLTNode* newnode = CreateSLTNode(x);
	if (phead == nullptr) {
		phead = newnode;
	}
	else
	{
		newnode->next = phead;
		phead = newnode;
	}

}

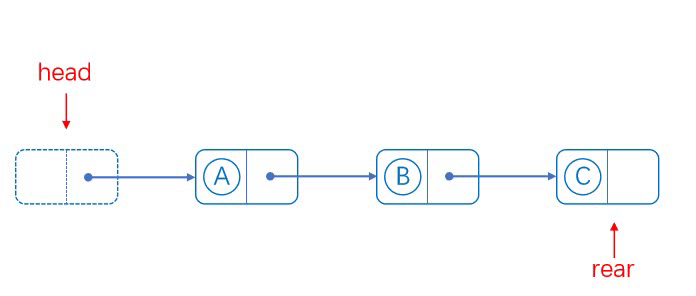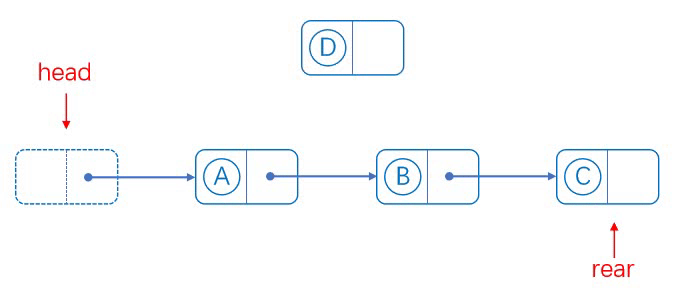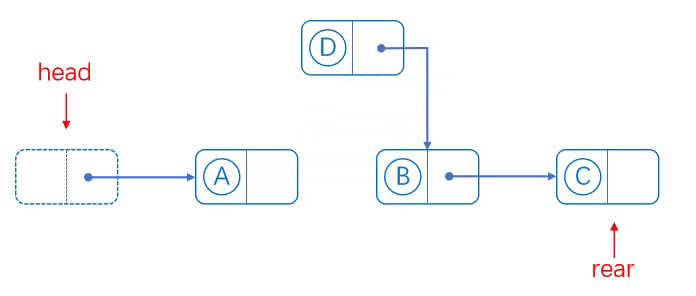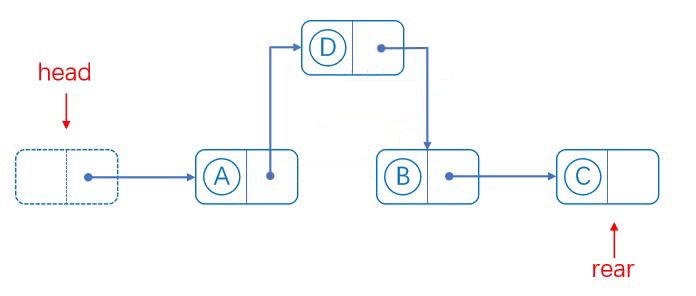
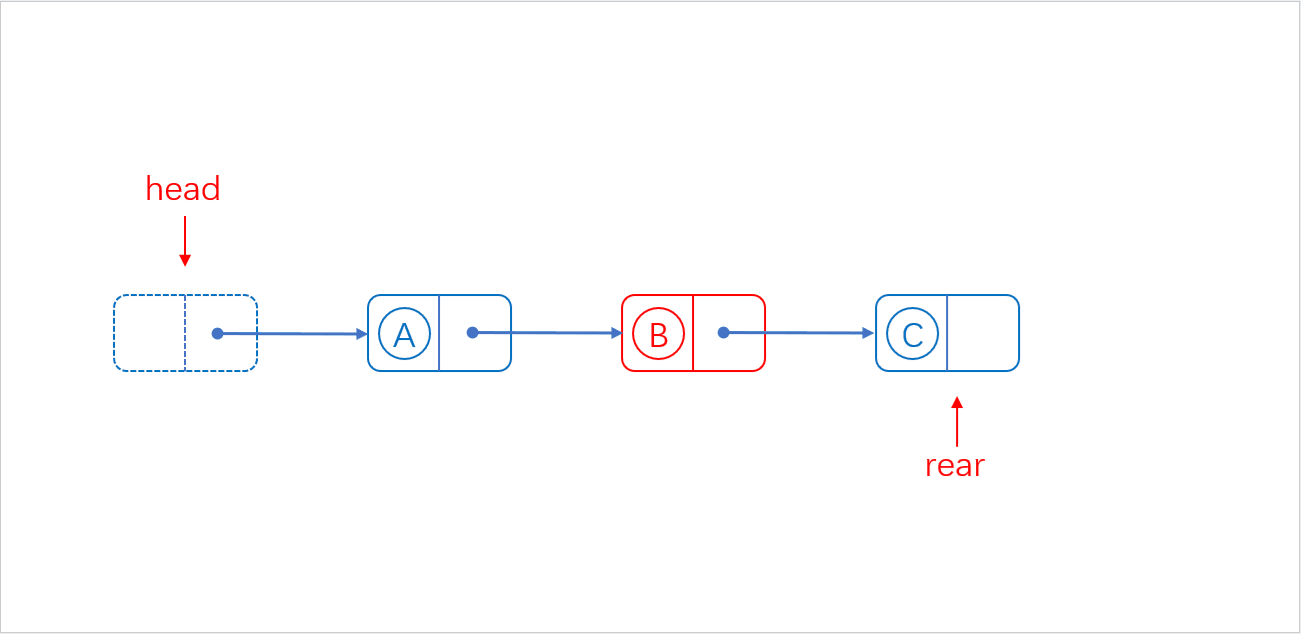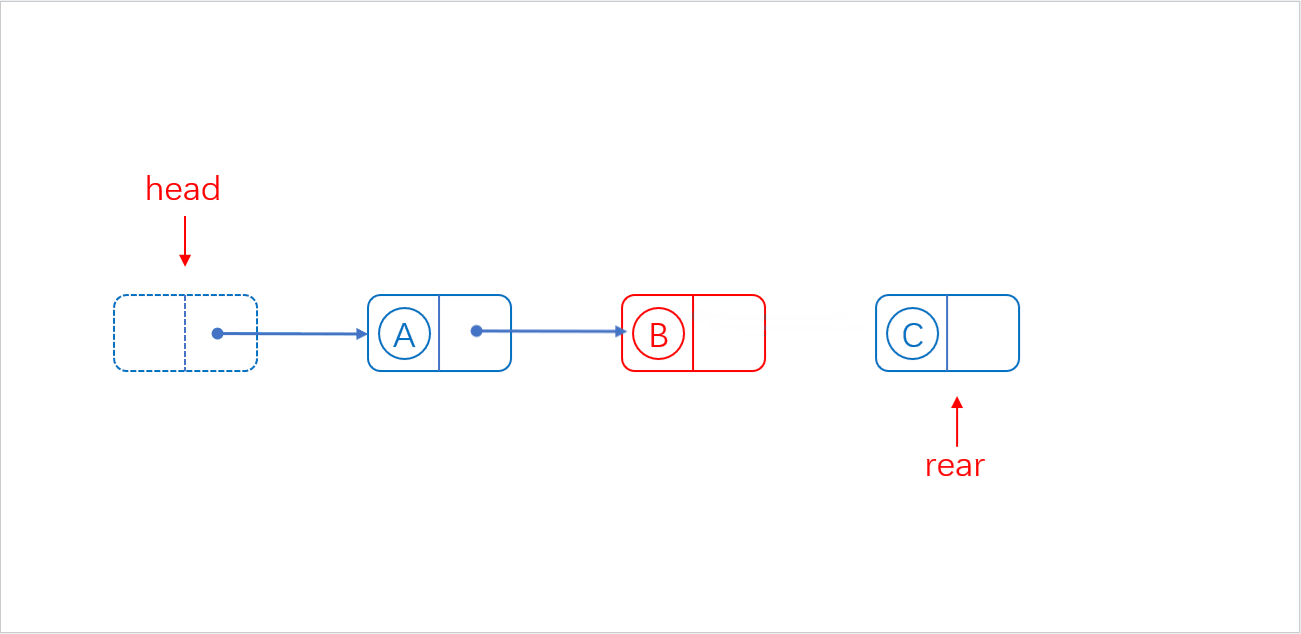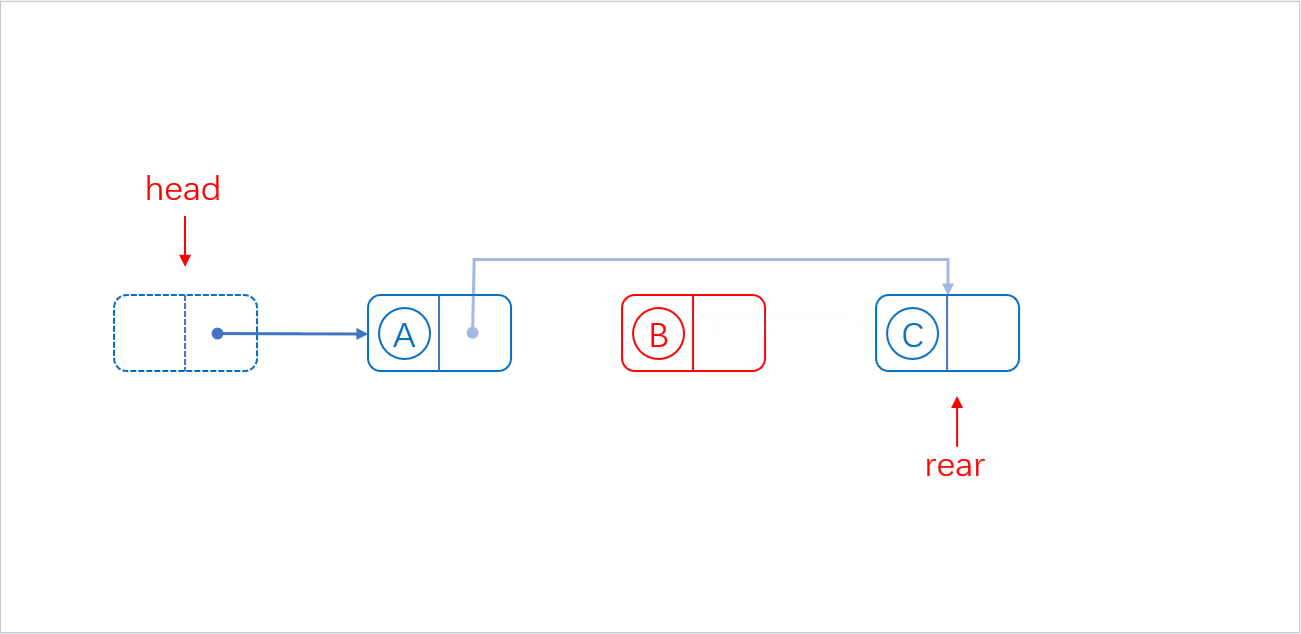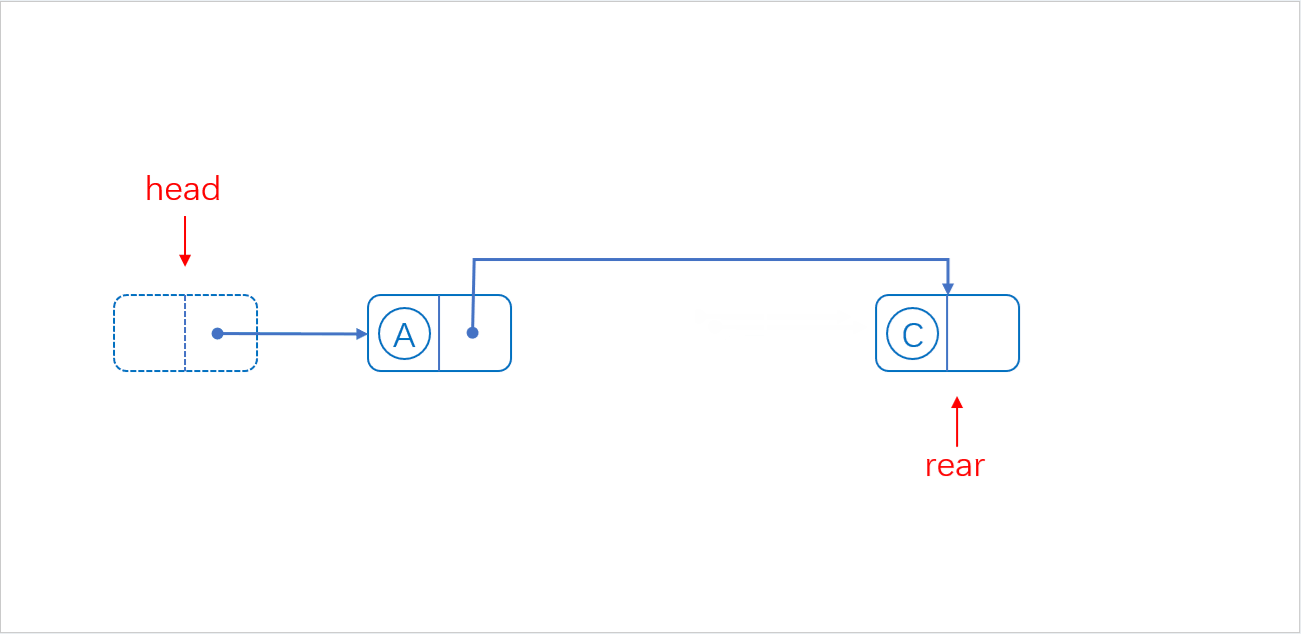
单链表pos位置后面插入：

实现思路：

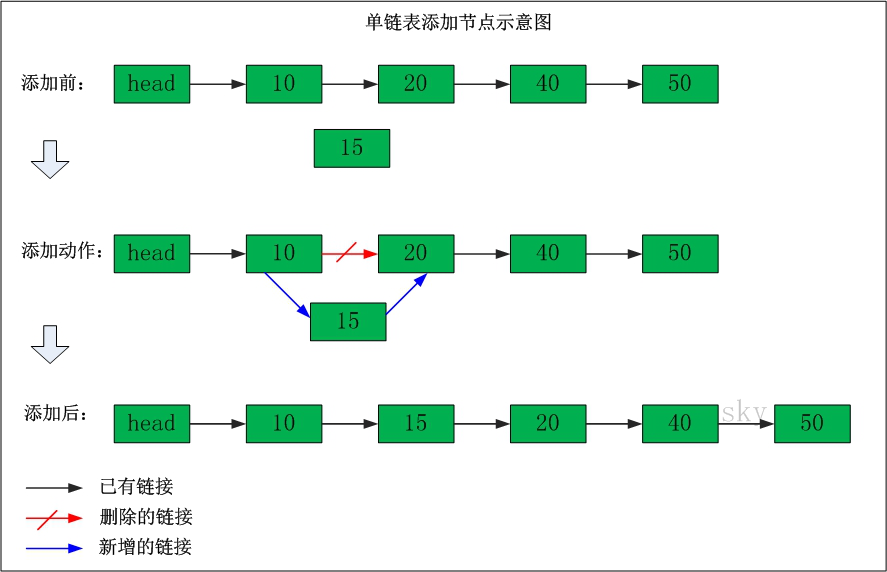
在目标位置处插入数据元素流程如下：
1、从头结点开始，提供cur指针定位到目标位置
2、从堆空间申请新的Node结点
3、将新结点插入目标位置，并连接相邻结点的逻辑关系。

对应图解：

 da

对应代码实现：

void SLTNodeInsert(SLTNode* pos, SLTDataType x)
{
	assert(pos);
	SLTNode* newnode = CreateSLTNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}

单链表尾删

实现思路

1.如果链表一个元素也没有则return

2.如果链表只有一个节点则将其置空，并将头节点置空

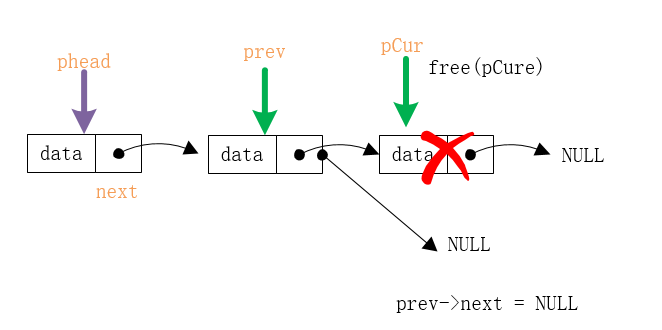
3.如果链表不止一个节点，我们则定义一个指针变量tail找尾，定义一个指针变量prev记录tail的前一个节点将prev->next指向tail->next，也就是prev->next=tail->next;在将尾部的节点释放

对应图解：

对应代码：

void SLTNodePopBack(SLTNode*& phead)
{
	if (phead == nullptr) {
		return;
	}
	else if (phead->next == nullptr) {
		free(phead);
		phead = nullptr;
	}
	else{


		SLTNode* prve = nullptr;
		SLTNode* tail = phead;
		while (tail->next)
		{
			prve = tail;
			tail = tail->next;
		}

		prve->next = tail->next;
		free(tail);
		tail = nullptr;
	}

}

单链表头删

实现思路：

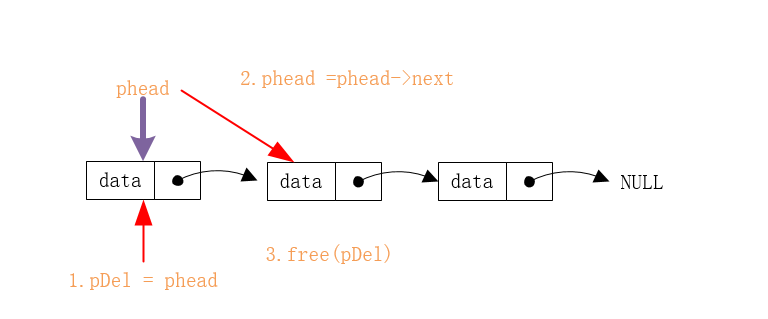
1.首先判断链表是不是空链表，如果是那么就return;

2.如果不为空那么我们定义一个指针变量记录头节点的下一个节点，在让下一个节点做新的头，在释放原来的头节点

对应代码：

void SLTNodePopFront(SLTNode*& phead)
{
	if (phead == nullptr) {//如果一个节点也没有就不用删了
		return;
	}
	else
	{
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}

}

单链表pos位置删除：

实现思路：

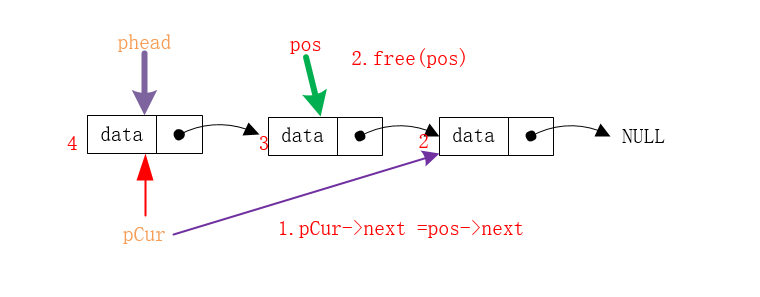
1.找到目标结点之前位置

2.提前保存目标结点后位置

3.销毁目标结点

4.链接原目标结点之前的位置与原目标结点之后的位置

代码实现：

 

void EraseCurrent(SLTNode*&phead,SLTNode* pos) {
	assert(phead && pos);
	if (phead == pos) {
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}
	else {
		SLTNode* cur = phead;
		SLTNode* prev = nullptr;//记录cur的前一个节点
		while (cur) {
			if (cur == pos) {
				break;
			}
			prev = cur;
			cur = cur->next;
		}
		if (cur) {
			prev->next = cur->next;
			free(cur);
			cur = nullptr;
		}


	}

}

或者这种写法也是可以的：

void SLTNodeErase(SLTNode*& phead, SLTNode* pos)
{
	assert(phead && pos);
	if (pos == phead){
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}
	else{
		SLTNode* cur = phead;
		while (cur->next != pos)
		{
			cur = cur->next;
		}
		cur->next = cur->next->next;
		free(pos);
		pos = nullptr;
	}

}

单链表的查找：

实现思路：

这个就比较暴力遍历一次链表，如果找到了就返回节点的指针，如果没有找到就返回NULL

代码实现：

SLTNode* SLTNodeFind(SLTNode* phead, SLTNode* pos)
{
	assert(pos && phead);
	SLTNode* cur = phead;
	while (cur)
	{
		if (cur->val == pos->val)
		{
			return cur;
		}
	}
	return nullptr;
}

单链表的销毁：

实现思路：

1.定义一个指针变量变量cur整个链表，在定义一个指针变量next记录cur的下一个节点

2.free(cur),在让cur指向下一个节点，即cur=next;

对应代码实现：

void SListDestory(SLTNode*&phead)
{
	SLTNode* cur = phead;
	while (cur)
	{
		SLTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	phead = nullptr;
}

代码汇总：

SList.cpp

#include"SList.h"
SLTNode* CreateSLTNode(SLTDataType x)
{
	SLTNode* newnode = new SLTNode(x);
	newnode->next = nullptr;
	newnode->val = x;
	return newnode;
}

void SLTNodePrint(SLTNode* phead)
{
	SLTNode* cur = phead;
	while (cur)
	{
		cout << cur->val << "->";
		cur = cur->next;
	}
	cout << "nullptr" << endl;

}

void SLTNodePushBack(SLTNode*&phead,SLTDataType x)
{
	SLTNode* newnode = CreateSLTNode(x);
	if (phead == nullptr) {
		
		phead = newnode;
		return;
	}

	SLTNode* tail = phead;
	while (tail->next)
	{
		tail = tail->next;
	}

	tail->next = newnode;
}
void SLTNodePopBack(SLTNode*& phead)
{
	if (phead == nullptr) {
		return;
	}
	else if (phead->next == nullptr) {
		free(phead);
		phead = nullptr;
	}
	else{


		SLTNode* prve = nullptr;
		SLTNode* tail = phead;
		while (tail->next)
		{
			prve = tail;
			tail = tail->next;
		}

		prve->next = tail->next;
		free(tail);
		tail = nullptr;
	}

}

void SLTNodePopFront(SLTNode*& phead)
{
	if (phead == nullptr) {
		return;
	}
	else
	{
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}

}

void SLTNodePushFront(SLTNode*& phead,SLTDataType x)
{
	SLTNode* newnode = CreateSLTNode(x);
	if (phead == nullptr) {
		phead = newnode;
	}
	else
	{
		newnode->next = phead;
		phead = newnode;
	}

}

SLTNode* SLTNodeFind(SLTNode* phead, SLTNode* pos)
{
	assert(pos && phead);
	SLTNode* cur = phead;
	while (cur)
	{
		if (cur->val == pos->val)
		{
			return cur;
		}
	}
	return nullptr;
}

void SLTNodeErase(SLTNode*& phead, SLTNode* pos)
{
	assert(phead && pos);
	if (pos == phead){
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}
	else{
		SLTNode* cur = phead;
		while (cur->next != pos)
		{
			cur = cur->next;
		}
		cur->next = cur->next->next;
		free(pos);
		pos = nullptr;
	}

}


void SListDestory(SLTNode*&phead)
{
	SLTNode* cur = phead;
	while (cur)
	{
		SLTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	phead = nullptr;
}

void SLTNodeInsert(SLTNode* pos, SLTDataType x)
{
	assert(pos);
	SLTNode* newnode = CreateSLTNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}

void SLTNodeEraseAfter(SLTNode* pos)
{
	assert(pos);
	SLTNode* next = pos->next;
	pos->next = pos->next->next;
	free(next);

}
void EraseCurrent(SLTNode*&phead,SLTNode* pos) {
	assert(phead && pos);
	if (phead == pos) {
		SLTNode* next = phead->next;
		free(phead);
		phead = next;
	}
	else {
		SLTNode* cur = phead;
		SLTNode* prev = nullptr;//记录cur的前一个节点
		while (cur) {
			if (cur == pos) {
				break;
			}
			prev = cur;
			cur = cur->next;
		}
		if (cur) {
			prev->next = cur->next;
			free(cur);
			cur = nullptr;
		}


	}

}

Test.cpp

#include"SList.h"

void TestSList()
{
	SLTNode* plist = nullptr;
	/*SLTNodePushBack(plist, 1);
	SLTNodePushBack(plist, 2);*/
	
	
	SLTNodePushFront(plist, 0);



	SLTNodePrint(plist);
}

int main()
{
	TestSList();
}

SList.h

#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
typedef int SLTDataType;
struct SLTNode
{
	SLTNode(SLTDataType x)
		:next(nullptr),val(x)
	{}
	SLTNode* next;
	SLTDataType val;
};

void SLTNodePrint(SLTNode* phead);

void SLTNodePushBack(SLTNode*& phead,SLTDataType x);

void SLTNodePopBack(SLTNode*& phead);

void SLTNodePopFront(SLTNode*& phead);

void SLTNodePushFront(SLTNode*& phead,SLTDataType x);

SLTNode* SLTNodeFind(SLTNode* phead, SLTNode* pos);

void SLTNodeErase(SLTNode*& phead, SLTNode* pos);

void SListDestory(SLTNode*&phead);

void SLTNodeInsert(SLTNode* pos, SLTDataType x);
void SLTNodeEraseAfter(SLTNode* pos);

 总结：

单链表增删查改时间复杂度分析：

增：

链表是通过记录头部地址来进行寻找后面数值的,所以需要遍历链表操作,如果在头部增,只需要查找一次,时间复杂度是 O(1),在尾部增需要查找n次,时间复杂度是 O(n).

删：

要遍历找到想要删除的数值,进行删除,对于链表,我们没法使用二分查找,只能遍历查找,找到该节点后删除,平均查找次数是n/2,时间复杂度是 O(n).

查：

要遍历查找,同样只能遍历查找,平均查找次数是n/2,时间复杂度是 O(n).

改：

要遍历找到想要更改的数值,同样只能遍历查找,平均查找次数是n/2,时间复杂度是 O(n).
 

 

如果觉得写的不错的话可以点个赞，如果有错误的话请在评论区留言谢谢！！！！ 

努力的图片 的图像结果


点击全文阅读


本文链接：http://m.zhangshiyu.com/post/40159.html

链表  结点  节点  
<< 上一篇 下一篇 >>

  • 评论（0）
  • 赞助本站

◎欢迎参与讨论，请在这里发表您的看法、交流您的观点。

最新文章

  • 江川赵玉梅是哪部小说的主角 江川赵玉梅全文阅读
  • 重生被夺身体前，拒当冤种嫁军官小说最新章节-主角苏在在苏秀秀全文免费阅读
  • 抖音爆款《快穿：女配逗比后，男主黑化了》林栀意沈之寒无广告阅读
  • 《未婚妻，你好甜》林安心白逸之最新章节在线阅读
  • 主角王川李高俊小说完整版-开局万法不侵，嚣张一点怎么了？免费阅读全文
  • 为白月光抛下我后，男友后悔了精彩小说-为白月光抛下我后，男友后悔了目录阅读
  • 叼着奶瓶的我被读心？颤抖吧反派们抖音全本小说温晚温溯抖音免费章节阅读
  • 萧琉月南宫墨小说《换我凤命？假千金重生后母仪天下》免费阅读
  • 好书推荐《余爱燃尽，当她让我妈变骨灰烟花》沈嫣然欧阳蓉儿许乐安全文在线阅读
  • 林澈程萱主角抖音小说《家族赶我走后，才发现我冠绝天下》在线阅读
  • 《寒武纪，我觉醒了空间之眼》精彩章节-寒武纪，我觉醒了空间之眼免费阅读全文
  • 七零：孟家的傻闺女变聪明了！(酣月十五)最佳创作小说全文在线阅读

    关于我们 | 我要投稿 | 免责申明

    Copyright © 2020-2022 ZhangShiYu.com Rights Reserved.豫ICP备2022013469号-1