引子

在了解结构体对齐规则之前，我们先来看一个例子
例1：

#include<iostream>
using namespace std;
struct Sut1
{
	char c;
	short st;
	int num;
}Sut1;
int main()
{
	cout << "sizeof(char) = " << sizeof(char) << endl;
	cout << "sizeof(short) = " << sizeof(short) << endl;
	cout << "sizeof(int) = " << sizeof(int) << endl;
	cout << "sizeof(Sut1) = " << sizeof(Sut1) << endl;
}

输出如下：
sizeof(char) = 1
sizeof(short) = 2
sizeof(int) = 4
sizeof(Sut1) = 8

结构体内各元素所占内存和为1+2+4=7，而结构体本身所占内存是8，居然不相等，那多出的那1个字节的内存到底去哪了呢？
仔细想了想有两种可能：

1. 结构体自身占1个字节，结构体所占内存总和为 自身的1个字节 加上 其内元素所占字节的总和
2. 结构体占据内存的多少,是由某种我们尚不了解的规则确定的

有了想法，就得验证，我们先验证第一个想法：

我们定义一个空的结构体，来看看其所占内存是不是1

#include<iostream>
using namespace std;
struct Sut1
{

}Sut1;
int main()
{
	cout << "sizeof(Sut1) = " << sizeof(Sut1) << endl;
}

为了让结果更使人信服，我用运行截图证明：

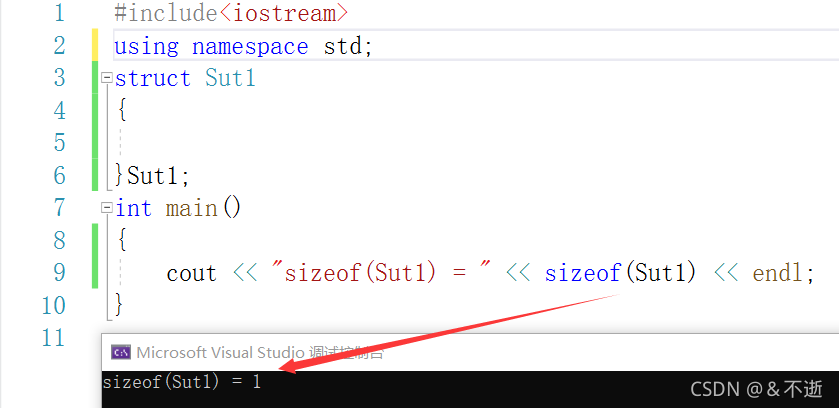
结构体本身所占内存果然是1，这不就证明了第一个想法是正确的吗！！！
好了本篇到此结束，谢谢观看。

开个玩笑哈，事情当然没有那么简单，这个例子只能证明一个空的结构体占一个字节，并不能证明第一个想法就是正确的。
证明失败…没事，再来一次，换个方式证明，我们看一下下面这个例子：
例2：

struct Sut1
{
	char c;
	int num;
	long long bigNum;
}Sut1;
int main()
{
	cout << "sizeof(long long) = " << sizeof(long long) << endl;
	cout << "sizeof(Sut1) = " << sizeof(Sut1) << endl;
}

输出：
sizeof(long long) = 8
sizeof(Sut1) = 16

如果第一个想法是正确的，那么sizeof(Sut1) = 结构体本身的1 + sizeof(char) +sizeof(int) + sizeof(long long) = 1+1+4+8 = 14 , 可是程序运行的结果是16。这一个反例足以证明第一个想法是错误的。

那么就只能是第二种想法了，结构体占据内存的大小 , 是受到某种规则确定的？是的，结构体在内存中的对齐规则，下面详细介绍

结构体的存储规则总览

我们先来看一下，到底是哪些规则总是让我搞不清结构体的大小(见一个打一个)
具体规则：

• 规则1： 结构体中的元素是按照定义的顺序逐个放到内存中去的，但并不是紧密排列的。从结构体存储的首地址开始，每一个元素放置到内存中时，它都会认为内存是以它自己的大小来划分的，因此元素放置的位置一定会在自己所占空间大小的整数倍上开始（以结构体变量首地址为0计算）。
• 规则2：如果一个结构体里嵌套一个结构体，则结构体成员要从嵌套的结构体内部最大元素大小的整数倍地址开始存储。
• 规则3：最后计算出结构体的总大小的时候，也就是sizeof(Sut1)，必须是其内部最大成员的整数倍，不足的要补齐。

一开始理解不了这些规则很正常，下面通过一些例子，讲解各个规则。

对规则1和规则3的运用

我们先利用规则1，计算前面 例1 和 例2 中结构体的大小。
例1例2忘了？那翻回上面看啊！啥？就不翻？那…我给你搬下来！

struct Sut1//例1
{
	char c;
	short st;
	int num;
}Sut1;
struct Sut2//例2
{
	char c;
	int num;
	long long bigNum;
}Sut2;

我们先来分析一下Sut1：

• 首先系统会将char型变量 c 存入第0个字节（就是结构体内存中第一个位置）
• 然后在存放short形变量 st 时，会以两个字节为单位进行存储（是因为short型占两个字节），由于第一个两字节模块已有数据(c占1个字节，另一个字节不存储元素)，因此它会存入第二个两字节模块，也就是存入到2~3字节位置，那个不存储数据的空间是对齐结构体元素浪费掉的空间。
• 紧接着存放int型变量num时，由于所占字节大小为4，其存放时会以4个字节为单位存储，也就是会找到第一个空的且是4的整数倍的位置开始存储，此例中，由于第一个4字节模块已被占用，所以将num存入第二个4字节模块。即4~7字节位置

Sut2和Sut1分析过程差不多，相信大家自己能分析出来。Sut1和Sut2存储示意图如下:

因此:

• Sut1所占内存大小为 1 + 1 + 2 + 4 = 8
• Sut2所占内存大小为 1 + 3 + 4 + 8 = 16

结合规则1和规则3，我们看下面一个例子
例3：

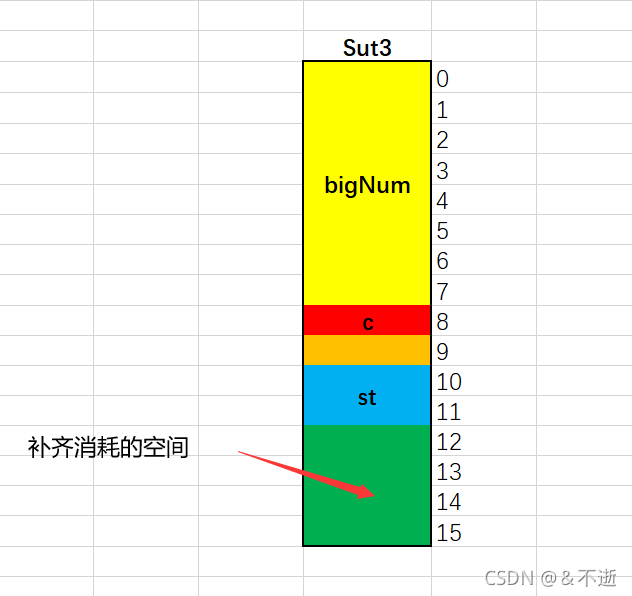
struct Sut3
{
	long long bigNum;
	char c;
	short st;
}Sut3;

如果仅仅按照规则1，我们计算出来的是sizeof(Sut3) = 8 + 1 + 1 + 2 = 12。
但其实际的大小是sizeof(Sut3) = 16。 因为规则3规定了，最后计算出的大小必须是其结构体内部最大成员的整数倍，不足的要补齐。
对于此例，结构体内部最大的成员是long long型，也就是8个字节大小。12不是8的整数倍，需要补齐，也就是补4个字节，结构体大小变为16。

我们再来看几个例子，强化对规则1和规则3的理解
例4：

struct Sut4
{
	long long bigNum;
	char c;
	int num;
	short st;
}Sut4;
struct Sut5
{
	char c1;
	long long bigNum;
	char c2;
	short st;
}Sut5;
struct Sut6
{
	//注意，无论什么类型的指针，都只占4个字节
	int *p1;
	long long bigNum;
	char c;
	char *p2;
	short st;
}Sut6;

我们对最复杂Sut6进行分析：

• 首先系统会将int*型指针变量 p1，以4个字节为单位进行存储（任何类型的指针都只占4个字节）， 存入第0~3字节空间。
• 然后存放long long形变量 bigNum 时，会以8个字节为单位进行存储，由于第一个8字节模块已有数据，因此它会存入第二个8字节模块，也就是存入到8~15字节空间。
• 紧接着存放char型变量c时，其只占1个字节，直接在后一个字节空间（第16个字节空间）中存入即可。
• 再然后在存放char*形指针变量 p2 时，会以4个字节为单位进行存储，由于前5个4字节模块已有数据，因此它会存入第6个4字节模块，也就是存入到20~23字节空间。
• 存放short形变量 st 时，会以2个字节为单位进行存储，存入到24~25字节空间。
• 最后总体占26个字节空间（0~25），不是最大成员long long型的整数倍，需要补齐到32个空间。

经过这几个例子，我相信你对规则1和3的理解已经很透彻了，接下来我们来看看规则2，结构体中嵌套结构体的存储规则该如何理解吧。

对规则2的应用

在一个结构体中嵌套一个结构体，这算是比较复杂的结构了，需要3个规则一起用。直接来看例子
例5：

struct Sut1
{
	short st;
	int num;
};
struct Sut2
{
	char c1;
	Sut1 sut1;
	char c2;
}Sut2;

根据前面的了解，我们可以很容易求得sizeof(Sut1) = 8 ，那如何求sizeof(Sut2)呢？先看一眼规则2：
如果一个结构体(Sut2)里嵌套一个结构体(Sut1)，则Sut1要从本身内部最大元素大小的整数倍地址开始存储。

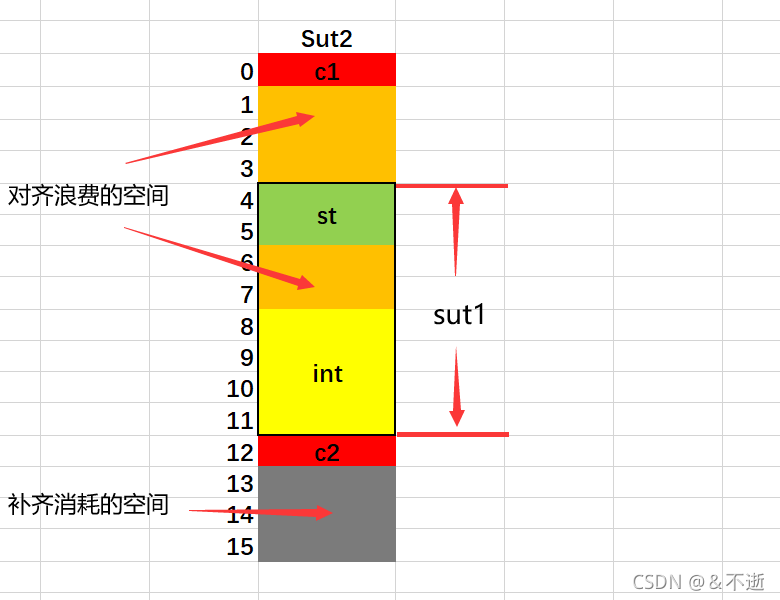
现在对Sut2进行分析：

• 把c1存储在第0字节空间上。
• sut1中最大元素是int型的num，占4个字节，所以sut1要在4的整数倍地址处存储，又因为sut1本身占8个字节空间，即在4~11字节空间上。
• 然后c2紧接其后，存储在第12字节空间上，此时结构体所占13个字节空间(0~12)，元素已经存储完毕，看看是否需要补齐，Sut2中(当然包括Sut1)最大的元素是int型的，占4个空间，因此补齐到4的整数倍16个字节空间

存储示意图如下：

接下来，来个头皮发麻的例子，这个例子弄懂了，这部分内容也就基本掌握了
例6：

struct Sut1
{
	char c;
	int num;
};
struct Sut2
{
	long long bigNum;
	int num;
};
struct Sut3
{
	int num;
	Sut1 sut1;
	double doub;
	Sut2 sut2;
	short st;
};

显然 sizeof(Sut3) = 48. 分析就不分析了，都是利用前面的规则，直接上图：

最优结构体

通过前面的这些例子我们了解到，结构体所占空间不仅与其内部元素的类型和数量有关，而且与不同类型元素的排列顺序有关。因此，对结构体内元素进行合理的排序尤为重要。
最优结构体：
一个确定了元素类型及数量的，通过一定顺序对其内元素进行排列后所占空间最小的结构体，称之为最优结构体

接下来我们通过一个例子讲解最优结构体如何得到：
例7：

struct Sut
{
	char c;
	long long bigNum;
	int num;
	double doub;
	short st;
};

我们现在很容易求得sizeof(Sut) = 40。从下面图中，我们发现总共浪费了7+4+6=17个字节空间，浪费了接近一半的空间啊！看着都心疼。

我们尝试将这个结构体优化成最优结构体，看看能节省多少空间。
优化原则非常简单，把占据内存较小的元素排在前面。
最优结构体如下：

struct Sut
{
	char c;
	short st;
	int num;
	long long bigNum;
	double doub;
};

它只占24个字节空间！比优化前节省了16个空间！
同时我们也发现最优结构体不是唯一的，比如把long long型数据和double型数据交换位置，它占的空间依然是24，也是最优结构体。

好了，本文到这里真的结束了，你的点赞、评论、关注、收藏都是对我最大的支持，谢谢！