一、前言

CRITIC权重法是一种比熵权法和标准离差法更好的客观赋权法：

• 它是基于评价指标的对比强度和指标之间的冲突性来综合衡量指标的客观权重。考虑指标变异性大小的同时兼顾指标之间的相关性，并非数字越大就说明越重要，完全利用数据自身的客观属性进行科学评价。

• 对比强度是指同一个指标各个评价方案之间取值差距的大小，以标准差的形式来表现。标准差越大，说明波动越大，即各方案之间的取值差距越大，权重会越高；

指标之间的冲突性，用相关系数进行表示，若两个指标之间具有较强的正相关，说明其冲突性越小，权重会越低。

对于 CRITIC 权重法而言，在标准差一定时，指标间冲突性越小，权重也越小；冲突性越大，权重也越大；另外，当两个指标间的正相关程度越大时，（相关系数越接近1），冲突性越小，这表明这两个指标在评价方案的优劣上反映的信息有较大的相似性。

在用 Python 复现 CRITIC 权重法时，需要计算变异系数，以标准差的形式来表现，如下所示：

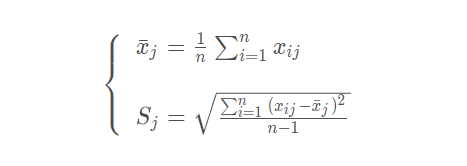
Sj表示第 j 个指标的标准差，在 CRITIC 权重法中使用标准差来表示各指标的内取值的差异波动情况，标准差越大表示该指标的数值差异越大，越能放映出更多的信息，该指标本身的评价强度也就越强，应该给该指标分配更多的权重。

研究收集到湖南省某医院 2011 年 5 个科室的数据，共有 6 个指标，当前希望通过已有数据分析各个指标的权重情况如何，便于医院对各个指标设立权重进行后续的综合评价，用于各个科室的综合比较等。数据如下：

二、详解计算均值和标准差

初始化一个简单的矩阵：

a = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
    ])
a

分别计算整体的均值、每一列的均值和每一行的均值：

print("整体的均值：", np.mean(a))              # 整体的均值
print("每一列的均值：", np.mean(a, axis=0))    # 每一列的均值
print("每一行的均值：", np.mean(a, axis=1))    # 每一行的均值

分别计算整体的标准差、每一列的标准差和每一行的标准差：

print("整体的方差：", np.std(a))              # 整体的标准差
print("每一列的方差：", np.std(a, axis=0))    # 每一列的标准差
print("每一列的方差：", np.std(a, axis=1))    # 每一行的标准差

结果如下：

三、实践：CRITIC权重法计算变异系数

导入需要的依赖库：

import numpy as np
import pandas as pd

提取数据：

df = pd.read_excel("./datas/result03.xlsx")
df

datas = df.iloc[:, 1:]
datas

如下所示：

数据正向和逆向化处理：

X = datas.values
xmin = X.min(axis=0)
xmax = X.max(axis=0)
xmaxmin = xmax - xmin
n, m = X.shape
print(m, n)
for i in range(n):
    for j in range(m):
        if j == 5:
            X[i, j] = (xmax[j] - X[i, j]) / xmaxmin[j]   # 越小越好
        else:
            X[i, j] = (X[i, j] - xmin[j]) / xmaxmin[j]   # 越大越好

X = np.round(X, 5)
print(X)

如下所示：

按列计算每个指标数据的标准差：

发现结果与文档不一致：

原因：numpy默认是除以样本数，求的是母体标准差；而除以样本-1，得到的才是样本标准差，这时设置参数 ddof=1 即可！

如上图所示，这下与文档里的结果一致了！

推荐阅读：
CRITIC权重法