前言
本文将探究MySQL索引结构的技术选型,分析哈希表、二叉搜索树、AVL树、红黑树、B树与B+树各自的优缺点。
解释了MySQL最终选择B+树作为其索引的组织方式的原因,并在最后增加了3道常问的面试题。
哈希表(Hash)
哈希表查询数据的时间复杂度为O(1),是一种高效的数据结构。面试中常问的HashMap就是基于哈希表的思想,对HashMap不太深入的同学,可以参考我的另外一篇文章HashMap夺命连环问
例如将索引列作为key,对应行的物理地址作为value,非常适用于处理等值查询。
select * from user where id=1;但哈希表显而易见的缺点就是,哈希表不适用于范围查找。
例如执行以下语句时,哈希表就无能为力了。
select * from user where id>1;二叉搜索树(Binary Search Tree)
经常刷LeetCode的同学,肯定是知道二叉搜索树的中序遍历是一个递增序列。
一颗二叉搜索树,每个节点最多只有2个子节点,左子节点的值小于父节点,右子节点的值大于父节点。
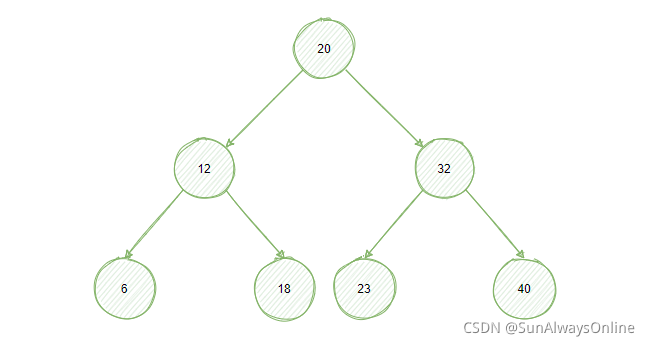
在二叉搜索树中进行查询,可以利用到二分查找,因此查询的时间复杂度为O(logN)。
例如查找元素23时,先从根节点开始,因为23>20,路由到右子节点32上。因为23<32,路由到其左子节点23上,发现相等,查询结束。
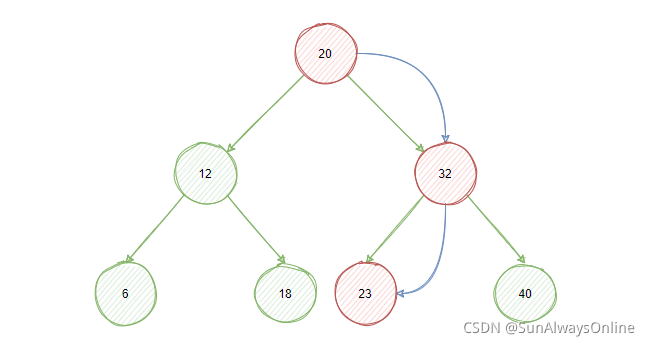
仅需比较3次,就可以查询到想要的数据。
另外,二叉搜索树的插入与删除操作的时间复杂度也为O(logN),有兴趣的同学可以做做LeetCode上的这道题701. 二叉搜索树中的插入操作
我们大可以将索引列作为节点的值,同样每个节点还有个用于保存相应行物理地址的变量。
二叉搜索树支持范围查找,例如对以下的sql语句
select * from user where id>12 and id<32;首先利用二分查找到节点12,再对此节点进行中序遍历,在遍历到节点32时停止即可。
二叉搜索树在搜索、插入与删除保持较优的时间复杂度,而且又支持范围查找。那MySQL为啥没有使用它呢?
是因为二叉搜索树在插入、删除的过程中并不会保持自身的平衡!
例如我新增了3条用户数据,初始的树是这样的(节点的值为主键):

当我再次增加3条数据后,节点被依次加在右子树上,最终形成链表的结构。
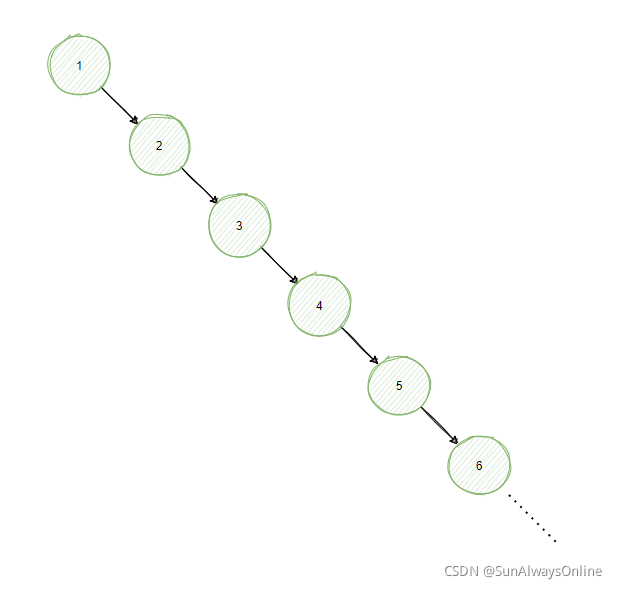
此时,二叉搜索树退化成了链表,时间复杂度由O(logN)提升到了O(N),查询性能大大降低。
因此,我们迫切需要一种能够在变动中保持自平衡的二叉树。
平衡二叉搜索树
AVL树
AVL树就是一种自平衡的二叉搜索树,对于它的任意一个节点,其左子树高度与右子树高度差最大为1,因此就不存在二叉树退化为链表的极端情况。
下图就是一个AVL树:
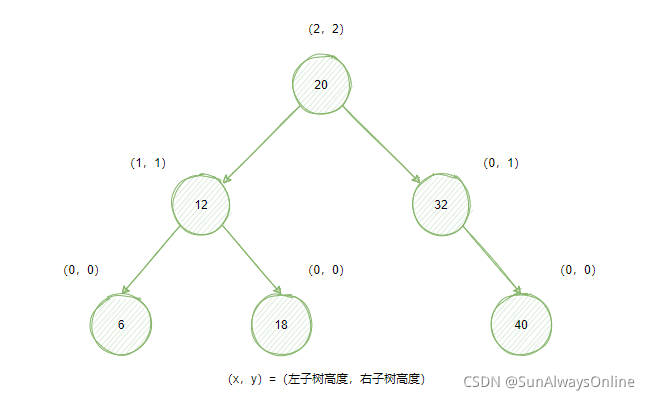
在往AVL树中插入节点时,需要通过左旋右旋操作来保证树的平衡性。
AVL树在查找、插入与删除操作的时间复杂度都为O(logN)。
AVL树追求极致的平衡性,因此就会进行多次的旋转。在插入与删除次数比较多时,达成平衡的代价甚至比使用它的收益还要大。
那有没有一种能够稍微降低点平衡性,却能带来较大的整体性能上提升的平衡二叉搜索树呢?
红黑树
红黑树也是一种平衡二叉搜索树,相比于AVL树。红黑树似乎对平衡性的追求没有那么执着,红黑树只要求最长路径不能超出最短路径的两倍。
在红黑树中,节点要么是红色,要么是黑色。根节点与叶子节点(NIL)都是黑色的,任意一个路径不能连续出现2个红色节点。从根节点出发的所有路径,黑色节点(不包含NIL)的数量都是相同的。
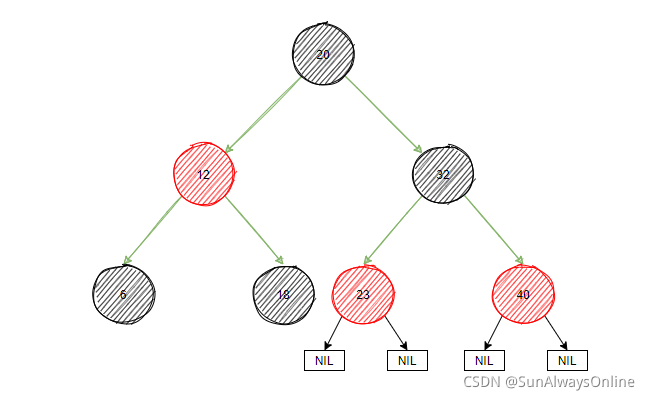
(不会有人没看出来,我拿的是一开始的那张图吧)

红黑树通过左旋、右旋与变色三种操作来保证一定的平衡性,相比于AVL树,红黑树的查询效率较低,但是删除与插入的效率大大提高,总体性能优于AVL树。
而且在实际的应用中,红黑树的应用更加广泛。例如HashMap在链表长度大于8时则转化为红黑树,TreeMap使用红黑树来对键值进行排序,IO多路复用中epoll使用红黑树来对Socket进行管理。
那MySQL为啥没有使用红黑树来组织索引数据呢?
如果索引数据能够一次性加载到内存中,那么使用红黑树是没有问题的。
问题就在于,索引数据无法一次性加载到内存中,因此索引数据需要分批加载。
假设要查询的数据位于叶子节点上,树高为n。第一次先把根节点加载到内存中,进行一次磁盘IO。当一直查询到叶子节点时,就需要进行n次IO。
当单表数据达到100万时,树的高度约为log1000000(以2为底)=20。一次磁盘IO平均耗时10ms,20次就是0.2秒。如果再考虑到范围查询、不走索引的查询与多表联查,速度慢得令人发指。
因此,我们现在的首要目标,就是降低IO次数,也就是降低树的高度。
B树
B树又称为B-树,注意不是B减树啊,“-”是一个连字符!!!
B树是一种多叉平衡搜索树,在节点总数相同的情况下,B树的高度明显低于二叉树。
B树有以下几个重要的特性:
- 每个节点可能存储多个元素,节点内元素是有序的,每一个元素也会对应一份数据行(当然也有可能是主键索引项,或者数据行的地址)。
- 父节点中的元素不会出现在子节点当中
- 叶子节点都在同一层,且之间没有通过指针相连
一颗具有3个分叉的B树为:

可以看到,B树的高度被压缩得很厉害。
另外一个方面,B树充分利用到了程序访问的局部性原理。也就是说,当程序访问磁盘或内存中的一份数据时,其周围的数据将会有很大概率在接下来被使用到。
因此,B数每个节点不会只存一个元素,而是存储多份。我们查询数据时,每进行一次IO,就会将B树的一个节点读进缓存中。这样在接下访问其周围的数据时,无需从磁盘读取,直接从缓存读取,缓存命中率大大提升。
也许会有人问?如果一个节点内存放大量元素,那么从磁盘读取的速度是否和个数相关,呈线性增长呢?
答案是不会的。第一次读取一个节点时,进行的是随机读,需要先进行磁盘寻道,是非常耗时的。之后读取其他的元素,是进行的顺序读。之所以进行顺序读,是因为一个节点内的元素被顺序存储在磁盘上的。顺序读是非常快速的,其效率可能千倍于随机读。
那么,在B树上读取索引项为21的流程是怎样的呢?
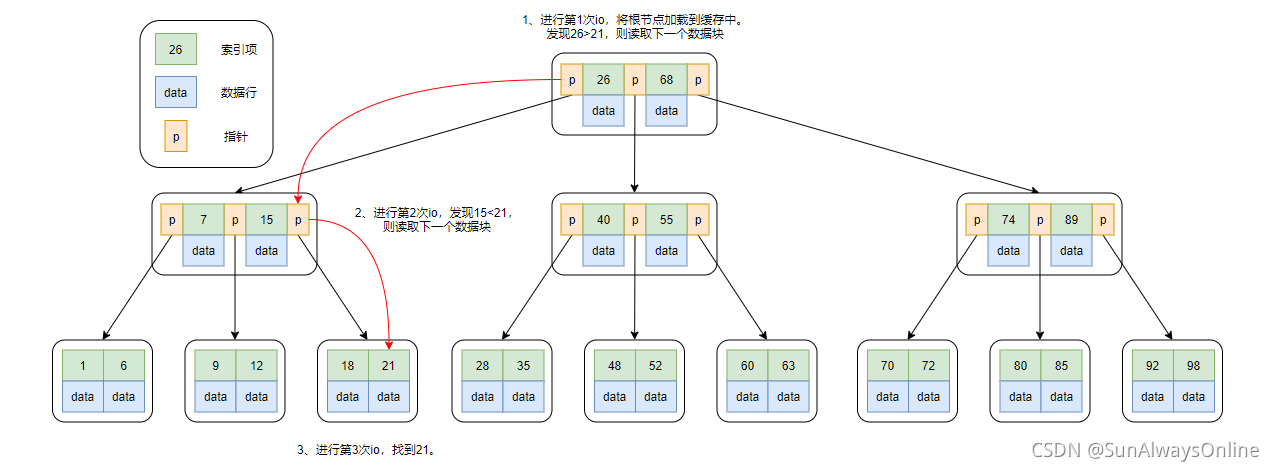
在节点内部,使用的是二分查找,用于找到下层指针。
看来B树能有效解决平衡二叉树io次数过多的问题,似乎已经能满足所有的要求了。
但是MySQL最终采用的B+树,而不是B树。

相对来说,B树还有以下的不足:
- 每个节点不仅存索引项,又存具体的数据,那么每个节点可存放的索引项就比较少。索引项少,io次数就会变多。
- B树不能做到快速的范围查找,需要进行多次的查找,类似于中序遍历。
为了改进B树,后来提出了B+树。
B+树
这个时候你又可以读作B加树了...
B+树有以下的特性:
- 非叶子节点只存放索引项,叶子节点既存放索引项,也存放具体的数据。
- 叶子节点会存放当前所有的索引项,就是说,可以与父节点的索引项重复。
- 叶子节点通过指针相连,形成有序的双向链表结构。
一颗成熟的B+树,应该是有如下的作风:
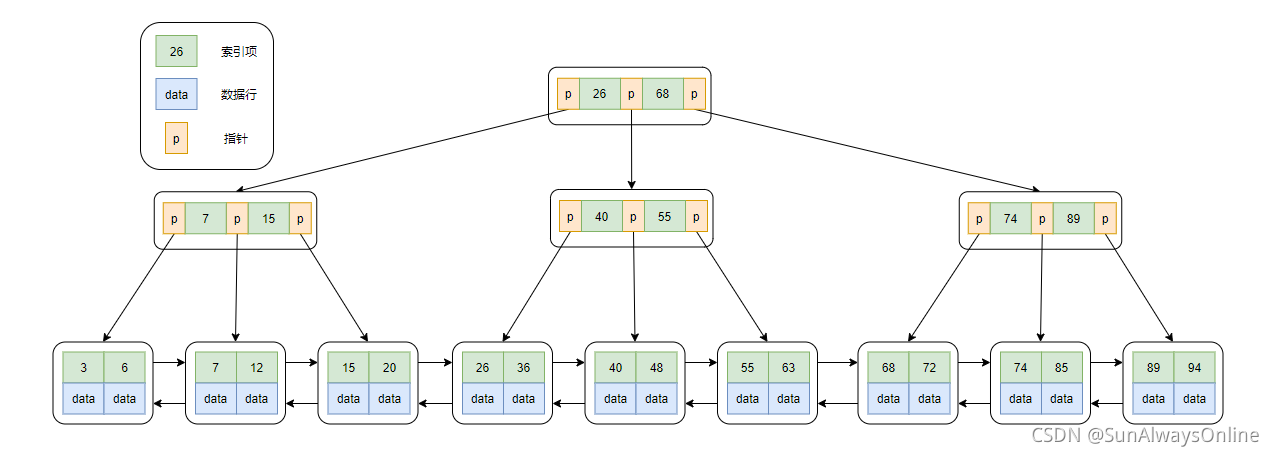
由于B+树叶子节点才存放数据行,因此每次的查询,都需要加载到叶子节点。而B树每个节点都存放数据行,每次的查询不一定非要到叶子节点。
所以这个时候会有人发出这样的疑问:B+树每次查询必须要深入到叶子节点,那么它的平均查询效率不是应该低于B树的吗?
如果在树高相同的情况下,确实是的。可实际情况是,在索引项相同的情况下,B+树的高度明显低于B树的,因为B+树的非叶子节点可以比B树存放更多的元素,毕竟少了数据行嘛。所以考虑到io成本加上范围查询,B+树的整体查询效率是优于B树的,但B+树对单个数据的查询效率是低于B树的。
B+树在范围查询上,是怎么表现出不错的性能的呢?
首先查找到范围下限,直接使用叶子节点的指针来加载下一个数据块,避免通过父节点来中转。在遍历到范围上限后,直接返回遍历到的所有数据即可。
B+树通过在叶子节点重复存储元素,其整体占用的空间其实是略高于B树的。但这点浪费的空间却能够换来巨大的性能提升,也是蛮不错的。
鉴于B+树用于以上的优点,MySQL最终采用了B+树作为索引的组织方式。
各种数据结构的对比
在这里直接以最简单明了的方式突出各个数据结构的优缺点:
| 数据结构 | 特点 | 优点 | 缺点 |
| 哈希表 | 使用哈希算法,快速查找 | 查询效率O(1) | 无法满足范围查找 |
| 二叉搜索树 | 使用二分查找算法,效率较高,且基本实现范围查找 | 正常情况下,操作效率为O(logN) | 极端情况下退化为链表 |
| AVL树 | 通过左旋、右旋实现严格自平衡 | 保持自平衡,操作效率为O(logN) | 追求极致的平衡,因此旋转效率低,IO次数多 |
| 红黑树 | 通过左旋、右旋与变色实现非严格自平衡 | 不追求极致平衡,整体性能高 | 实现复杂,IO次数多 |
| B树 | 多叉查找,一个节点存放多个索引项,也存放具体数据 | 树的高度较低,IO次数少 | IO次数、范围查找还有优化的空间 |
| B+树 | 非叶子节点仅存放索引项,叶子节点为双向链表 | 树的高度更低,IO次数更少 | 存储重复索引项,内存空间占用相对多一点 |
加餐
使用二级索引查询数据,经历的io次数怎么算?
二级索引也是使用B+树来组织的,其叶子节点不是存储具体的数据行,而是存储的主键值。
先通过在二级索引中查询到主键值,再进行回表查询主键索引树,所以一共需要经历的io次数=二级索引树io次数+主键索引树次数
有些同学可能会有一点想法,为什么二级索引的叶子节点不直接存储具体的数据,再回表一次不是降低了效率吗?
一个表会有多个索引,如果每个索引数都保存一份全表数据,数据冗余度就会非常高!
3层的B+树,大概可以存放多少条数据?
InnoDB每次会从磁盘中读取一页的数据,一页大小为16KB,当然可以通过参数设置,因此B+树中一个节点的大小一般也为16KB。
假设这16KB全部用来存储节点数据,当然其中会有一小部分用来存储元数据,可以忽略不计。
B+树中的一个节点,包含索引项与指向下层的指针。
如果此时以int类型的主键作为索引项,int类型占用4个字节,指针占用6个字节。因此根节点拥有的索引项数为16KB/10B=16*1024/10=1638个。
则根节点拥有1638个子节点,且第二层也是非叶子节点,因此第二层能存放的索引项数为1638*1638约等于268万个。
第三层为叶子节点,叶子节点存放索引项、前驱后驱指针与具体数据,具体的数据肯定是比索引项与指针大得多的,这时候就统一按一行数据1KB计算,也就是一个叶子节点可以保存16条数据。
那么3层的B+数总共可以保存的数据行为2683044*16≈4千万条。
当然,2层的B+树可以保存的数据行为1638*16≈3万条。
为什么MongoDB直接使用B树?
MySQL作为一种关系型数据库,大部分的情况下会进行多表联查,多表联查就涉及到对某个表的遍历。而B+树叶子节点存在双向指针,对遍历支持友好。
而MongoDB作为一种非关系的文档数据库,使用一种类似json格式来保存数据,在以上的背景下,MongoDB认为单次查询比范围查询使用更加广泛。B树的每个节点都保存具体数据,因此可能在跟节点直接查找到数据就返回,单次查询效率高于B+树。
不过有意思的一点是,MongoDB和MySQL一样,底层均使用了可插拔的存储引擎。MongoDB其默认的引擎为WiredTiger,其引擎作者自身表明了内部其实是使用B+树来作为索引的组织方式的,详情见这篇文章http://source.wiredtiger.com/3.2.1/tune_page_size_and_comp.html
我希望以这篇文章为开端,激发各位读者对新知识的探究。其实结论对错并不重要,可贵的是探讨的过程。