C语言每日一练
2021年11月19日

题目描述

甲、乙、丙三位渔夫出海打鱼，他们随船带了21只箩筐。当晚返航时，他们发现有7筐装满了鱼，还有7筐装了半筐鱼，另外7筐则是空的，由于他们没有秤，只好通过目测认为7个满筐鱼的重量是相等的，7个半筐鱼的重量是相等的。在不将鱼倒出来的前提下,怎样将鱼平分为3份？

分析

这题还有两个隐形要求：三个人分得的箩筐数量相同（7只）；列出所有的平分方法。

我的思路（参照网上他人方法）
首先，所有的鱼所占的箩筐数为7+7*0.5=10.5只（7只满筐和7只半筐），将它们平分成3份，那么每个人就能分到3.5只装满鱼的箩筐（例如3只满筐和1只半筐或者1只满筐5只半筐等等）。

我们可以先遍历出甲分到的装满鱼的箩筐数，然后再遍历出乙分到的装满鱼的箩筐数，丙的满筐鱼箩筐数则为7-甲乙的满筐鱼的箩筐数之和。由于最后每个人都能分到3.5筐鱼，所以他们最多可分配3只装满鱼的箩筐。

确定完他们的满筐鱼箩筐数之后，接着遍历甲乙分到的半筐鱼箩筐数，丙分到的半筐鱼箩筐数则等于7-甲乙的半筐鱼的箩筐数之和。由于目前他们分到的满筐鱼的箩筐数为整数，而最终他们都必须分得3.5筐鱼，所以每个人至少要分到一只装有半筐鱼的箩筐，且一定是奇数只。

在分配完半筐鱼的箩筐后，如果每个人所分到的鱼的箩筐数为3.5（其实判断甲乙即可），那么说明该分配方式符合条件。

最后，每个人空筐的箩筐数=7-该人的满筐鱼箩筐数-该人的半筐鱼箩筐数。

我的代码还有一些可优化的地方（可以删去一些无效的循环次数），在网上参考部分有一个很不错的例子（我的思路和代码就参考了该例子）。

代码实现

#include <stdio.h>

int main()
{
    //甲乙丙分得的不同类型箩筐数量
    int fish_nums[3][3] = {0};
    int i = 0, j = 0, k = 0, m = 0, n = 0;

    //甲分满箩筐，最大3筐
    for(i = 0; i <= 3; i++)
    {
        fish_nums[0][0] = i; //甲分得满箩筐数
        //乙分满箩筐，最大三筐
        for(j = 0; j <= 3; j++)
        {
            fish_nums[1][0] = j;         //乙分得满箩筐数
            fish_nums[2][0] = 7 - i - j; //丙分得满箩筐数
            if(fish_nums[2][0] > 3)
                continue;                //超过3.5框

            //甲分奇数个半箩筐，最少1个，最多5个（其他人也要分）
            for(k = 1; k <= 5; k+=2)
            {
                if(fish_nums[0][0] + 0.5 * k == 3.5)
                    break;
            }
            fish_nums[0][1] = k;         //甲分得半箩筐数

            //乙分奇数个半箩筐，最少1个，最多5个（其他人也要分）
            for(m = 1; m <= 5; m+=2)     //乙分奇数个半箩筐
            {
                if(fish_nums[1][0] + 0.5 * m == 3.5)
                    break;
            }
            fish_nums[1][1] = m;         //乙分得半箩筐数
            fish_nums[2][1] = 7 - k - m; //丙分得半箩筐数

            //甲分得空箩筐数
            fish_nums[0][2] = 7 - fish_nums[0][0] - fish_nums[0][1];
            //乙分得空箩筐数
            fish_nums[1][2] = 7 - fish_nums[1][0] - fish_nums[1][1];
            //丙分得空箩筐数
            fish_nums[2][2] = 7 - fish_nums[2][0] - fish_nums[2][1];

            //打印匹配的结果
            for(n = 0; n < 3; n++)
            {
                if(n == 0)
                    printf("甲——");
                else if(n == 1)
                    printf("乙——");
                else printf("丙——");
                printf("满筐：%d，半筐：%d，空筐：%d\n", fish_nums[n][0],\
                        fish_nums[n][1], fish_nums[n][2]);
                if(n == 2)
                    printf("-------------------------------------\n");
            }
        }
    }
    return 0;
}

运行结果

由于我考虑了针对甲乙丙三个不同的人的分法，所以最后结果有6个，如果不考虑三个人的身份，那么分法还需要除以3，即只有2种（具体代码可以参考下文的网上参考部分）

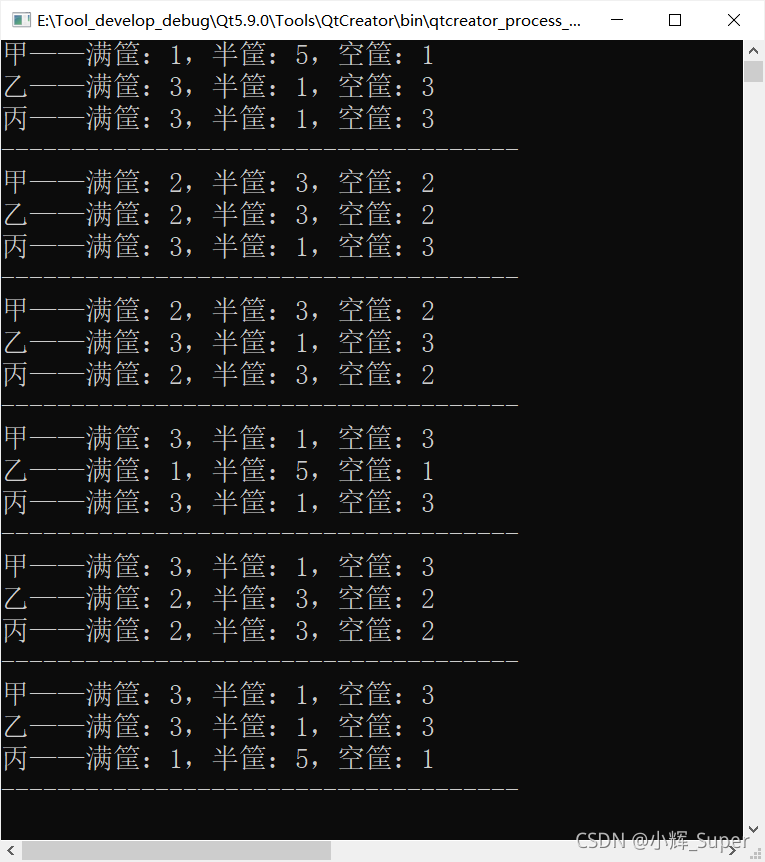
网上参考

原文链接：http://c.biancheng.net/cpp/html/3370.html

核心思路
(1) 数组的每行或每列的元素之和都为7。
(2) 对数组的行来说，满筐数加半筐数=3.5。
(3) 每个人所得的满筐数不能超过3筐。
(4) 每个人都必须至少有1个半筐，且半筐数一定为奇数。

#include<stdio.h>
int a[3][3], count;
int main()
{
    int i, j, k, m, n, flag;
    printf("It exists possible distribtion plans:\n");
    for(i=0; i<=3; i++)  /*试探第一个人满筐a[0][0]的值，满筐数不能>3*/
    {
        a[0][0]=i;
        for(j=i; j<=7-i&&j<=3; j++)  /*试探第二个人满筐a[1][0]的值，满筐数不能>3*/
        {
            a[1][0]=j;
            if((a[2][0]=7-j-a[0][0])>3)
                continue;  /*第三个人满筐数不能>3*/
            if(a[2][0]<a[1][0])
                break;  /*要求后一个人分的满筐数大于等于前一个人，以排除重复情况*/
            for(k=1; k<=5; k+=2)  /*试探半筐a[0][1]的值，半筐数为奇数*/
            {
                a[0][1]=k;
                for(m=1; m<7-k; m+=2)  /*试探半筐a[1][1]的值，半筐数为奇数*/
                {
                    a[1][1]=m;
                    a[2][1]=7-k-m;
                    /*判断每个人分到的鱼是 3.5筐，flag为满足题意的标记变量*/
                    for(flag=1,n=0; flag&&n<3; n++)
                        if(a[n][0]+a[n][1]<7&&a[n][0]*2+a[n][1] == 7)
                            a[n][2]=7-a[n][0]-a[n][1];  /*计算应得到的空筐数量*/
                        else
                            flag=0;  /*不符合题意则置标记为0*/
                    if(flag)
                    {
                        ++count;
                        printf("No.%d Full basket Semi-basket Empty\n", count);
                        for(n=0; n<3; n++)
                            printf(" fisher %c: %d %d %d\n",'A'+n, a[n][0], a[n][1], a[n][2]);
                    }
                }
            }
        }
    }
    return 0;
}

原文结果：